机械波的一般位置中“特殊点”的处理方法

付 岩

(吉林省长春市九台区实验高中)

机械振动与机械波是在时间和空间上表现出的周期性运动,学生要想很好地掌握本部分知识内容,必须具备一定的空间想象能力和抽象思维能力.纵观高考试题,考查形式有填空、选择、计算,内容主要包括对机械振动基本概念和规律的理解、波的多解处理方法、从振动图像和波的图像中获取信息的能力、通过振动和波的函数式考查运用数学知识处理物理问题的能力等,体现了高考评价体系中对物理学科提出的五种关键能力的考查.

本文结合实际教学,针对波动图像与振动图像,结合试题中出现的一类问题情境,进行归类探讨,助力相关学习与研究.

1 相关情境

质点的位移为零(平衡位置)或者最大值(波峰、波谷)时,习惯称该位置为“特殊位置”,学生对处于这些位置质点振动情况的分析较为容易,但某些试题的考查情境是质点在“非特殊位置”,如位移大小为这些位置也是有迹可循的,笔者在教学实践中常用“一般位置中的特殊点”这一说法,来特指处于上述位置的质点.

2 知识归类

2.1 波的图像中,一般位置中“特殊点”的横坐标特征

图1

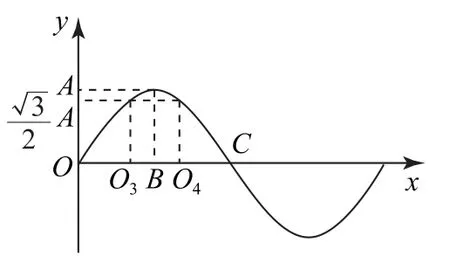
图2

综上可得出:点O1和O3将四分之一波长的OB三等分,四分之一波长的BC也同样被点O4和O2三等分,O3和O4将半波长三等分,如图3所示.

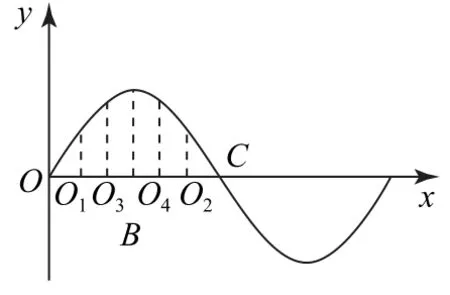
图3

通过以上类似分析,如图4 所示,位移为y＝的质点的平衡位置坐标将四分之一波长平分,与点C一同将半波四等分,即

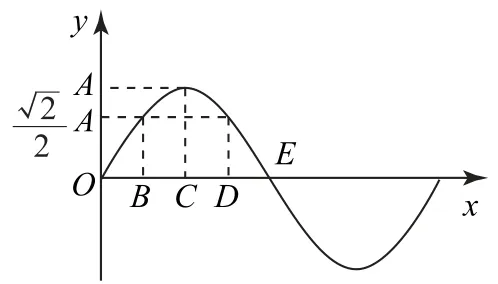
图4

2.2 振动图像中,一般位置中“特殊时刻”的时间特征

设某质点的振动图像为标准的正弦曲线(从t＝0时刻开始振动),如图5 所示,振动方程为y＝Asin(ωt).通过分析得到如表1所示的质点振动的时间特征:质点由平衡位置向上振动到位移为A2的时间与由A2振动到最大位移A4所用时间相等,为从平衡位置向上振动至位移为A1处的时间、由A1振动到A3的时间、由A3振动至最大位移A4时间相等,即

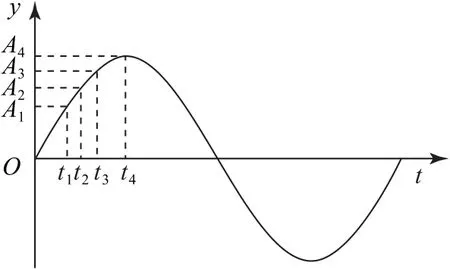
图5

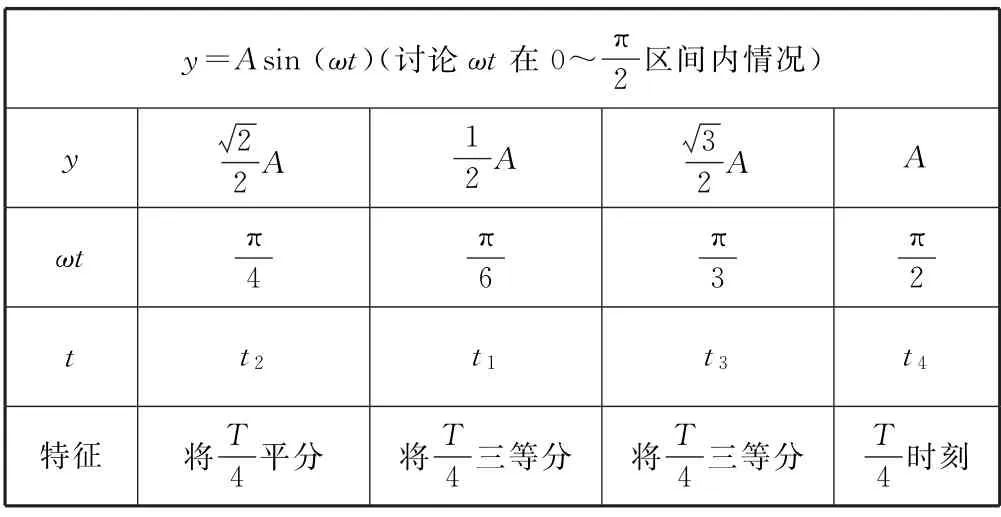
表1 质点振动的时间特征

2.3 常用规律

1)与质点位置无关:相隔半波长奇数倍的两质点振动步调始终相反;相隔波长整数倍的两质点振动步调始终相同.

2)与振动起点无关:经过半个周期,质点一定运动到对称点,且振动步调完全相反,路程为两倍振幅;经过n个周期,路程为4n倍振幅.

3 方法应用

3.1 巧解波长

例1(2022 年全国甲卷)一平面简谐横波以速度v＝2m·s－1沿x轴正方向传播,t＝0 时刻的波形图如图6所示.介质中平衡位置在坐标原点的质点A在t＝0 时刻的位移y＝cm.该波的波长为_________m,频率为_________Hz.t＝2s时刻,质点A_________(填“向上运动”“速度为零”或“向下运动”).

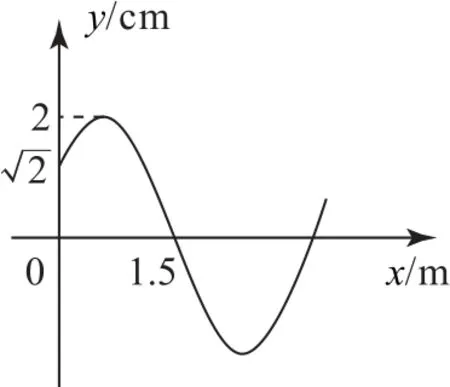
图6

解析

频率求解及振动方向的判断过程不赘述,主要分析对比求波长的方法.

方法1解析式法

方法2“特殊点”法

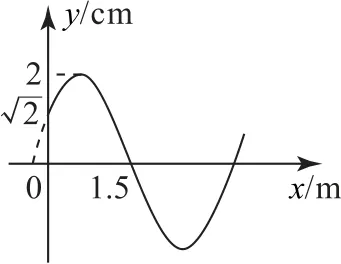
图7

3.2 判断周期

例2(2021 年湖北卷)一列简谐横波沿x轴传播,在t＝0 时刻和t＝1s时刻的波形分别如图8中实线和虚线所示.已知x＝0处的质点在0～1s内运动的路程为4.5cm.下列说法正确的是( ).

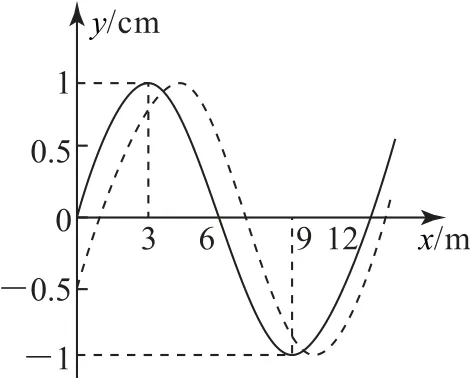
图8

A.波沿x轴正方向传播

B.波源振动周期为1.1s

C.波的传播速度大小为13m·s－1

D.t＝1s时,x＝6 m 处的质点沿y轴负方向运动

解析

由图像可得振幅A＝1cm,在Δt＝1s时间内x＝0 处的质点运动的路程为4.5cm＝由此判断出x＝0处的质点在t＝0时刻向下振动,波向正方向传播,故选项A 正确;t＝1s时刻该质点仍然向下振动,且位移恰好为－0.5cm,其大小是振幅的二分之一,根据前文图5及表1中的结论,直接得到Δt＝关系,解得T＝.选项C、D 不赘述.

4 总评

振动与波的图像问题中,对于位于“特殊位置”的质点,很容易套用结论解决问题,而处理一般位置时,多数教师选择的方法是根据题意,写出波(或质点振动)的函数式,将已知点坐标代入其中进而求出解析式,再处理相关问题.本文对一般位置中的“特殊点”提出的处理方法,其本质也是基于数学正弦函数的基本特征,进行归类总结,学生通过训练,能够很好地理解与运用,并在解决选择题、填空题以及验证计算时节省时间,达到事半功倍的效果.

(完)