高考对几何光学的考查解读
2023-02-27王辉
王 辉
(安徽省利辛县第一中学)
光学是高中物理重要组成部分之一,是高考必考内容.高考对几何光学的考查重点主要有光的折射定律和全反射、光速与折射率关系、折射率与频率的关系等.
几何光学问题的解题方法是根据题述情境,画出光路图,根据光路图中的几何关系找出入射角和折射角,利用折射定律和全反射的相关知识列方程解答.
1 透明球(或圆柱)模型
【命题方式】模型可能为透明球或圆柱,也可能为中空透明球或圆柱,光线可能从透明球或圆柱外面射入,也可能从透明球或圆柱内部射出.
例1(2022 年辽宁卷)完全失重时,液滴呈球形,气泡在液体中将不会上浮.2021 年12月,在中国空间站“天宫课堂”的水球光学实验中,航天员向水球中注入空气形成了一个内含气泡的水球.如图1所示,若气泡与水球同心,在过球心O的平面内,用单色平行光照射这一水球.下列说法正确的是( ).
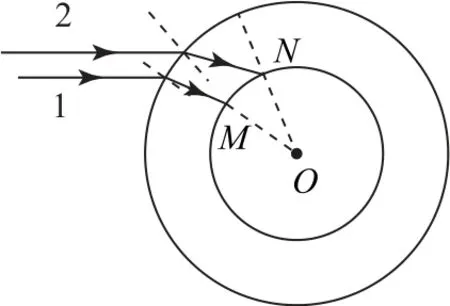
图1
A.此单色光从空气进入水球,频率一定变大
B.此单色光从空气进入水球,频率一定变小
C.若光线1在M处发生全反射,光线2在N处一定发生全反射
D.若光线2在N处发生全反射,光线1在M处一定发生全反射
解析
由于光的频率是由光源决定的,与介质无关,所以此单色光从空气进入水球,频率不变,选项A、B错误;由光路图可看出光线1入射到水球的入射角小于光线2入射到水球的入射角,则光线1在水球外表面折射后的折射角小于光线2在水球外表面折射后的折射角.设水球半径为R,气泡半径为r,光线经过水球后的折射角为α,光线进入气泡的入射角为θ,根据图2中几何关系,由正弦定理得而
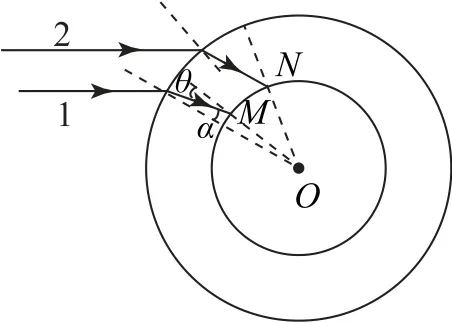
图2
【温馨提示】所有波传播过程中频率都不变.
2 玻璃砖模型
【命题方式】通常采用长方体玻璃砖、半圆形玻璃砖、梯形玻璃砖,光线一般从玻璃砖的某侧面射入.
例2(2021年海南卷)如图3 所示,长方体玻璃砖的横截面为矩形MNPQ,MN=2NP,其折射率为一束单色光在纸面内以α=45°的入射角从空气射向MQ边的中点O,则该束单色光( ).
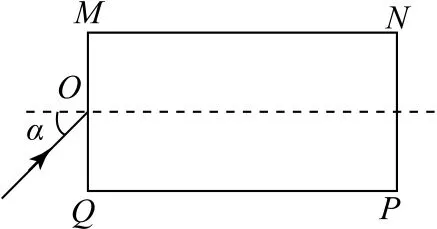
图3
A.在MQ边的折射角为60°
根据图1可以看出,在输出频率为32kHz的条件下电容变化比较稳定没有较多的噪声干扰,而在16kHz的频率条件下电容值变化出现了不稳定的状况。
B.在MN边的入射角为45°
C.不能从MN边射出
D.不能从NP边射出
解析
由sinC=可知全反射临界角C=45°.画出光路如图4所示,设从O点射入的光线的折射角为r,由折射定律有n=解得r=30°,即在MQ边的折射角为30°,选项A 错误.由几何关系可知,在MN边的入射角为60°,大于全反射临界角45°,所以光线不能从MN边射出,选项C 正确,选项B错误.射到NP边的光线入射角为30°,小于全反射临界角45°,所以能从NP边射出,选项D 错误.
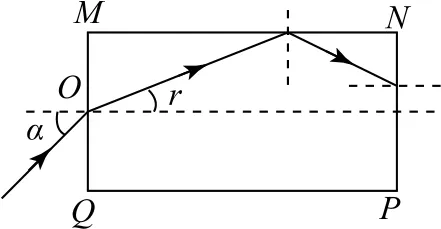
图4
【试题拓展】拓展试题并请读者自行解答:长方体玻璃砖的横截面为矩形MNPQ,其折射率为一束单色光在纸面内从空气射向MQ边的中点O,光线恰好在MN边发生全反射,则入射角的正弦值为多少?
3 三棱镜或组合体模型
【命题方式】通常采用三棱镜、三棱镜组合体、三棱镜与半圆组合体、三棱镜与圆柱组合体,光线一般从三棱镜或组合体的某侧面射入.
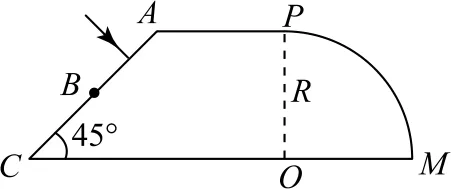
图5
A.仅有a光 B.仅有b光
C.a、b光都可以 D.a、b光都不可以
解析
当两种频率的细激光束从A点垂直于AB面入射时,激光沿直线传播到O点,经第一次反射沿半径方向直线传播出去,如图6所示.
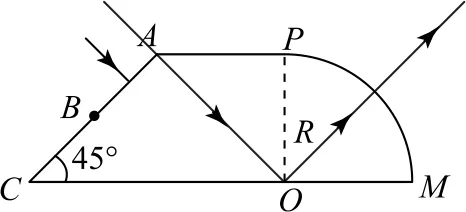
图6
保持光的入射方向不变,入射点从A向B移动过程中,由图中光路可知,激光沿直线传播到CO面经反射向PM面传播,根据图像可知,入射点从A向B移动过程中,光线传播到PM面的入射角逐渐增大.
如图8所示,当入射点为B点时,根据光的反射定律及几何关系可知,光线传播到PM面的P点,此时光线在PM面上的入射角最大,设为α,由几何关系得α=45°.
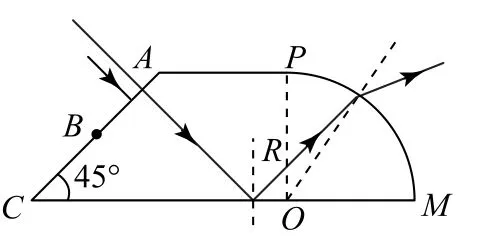
图7
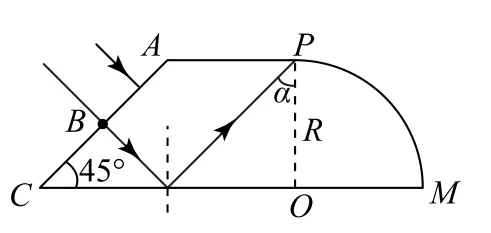
图8
【关键点拨】解题时只有考虑了各种可能情况,才能正确解答.
4 光在液体中传播模型
【命题方式】光在液体中的传播模型,包括光线从液面上方射入水中,光线从液体中射出水面,考查的知识点主要有光的折射定律、全反射和光速与折射率的关系等.
例4(2022 年新高考江苏卷)如图9所示,两条距离为D的平行光线,以入射角θ从空气射入平静水面,反射光线与折射光线垂直,求:
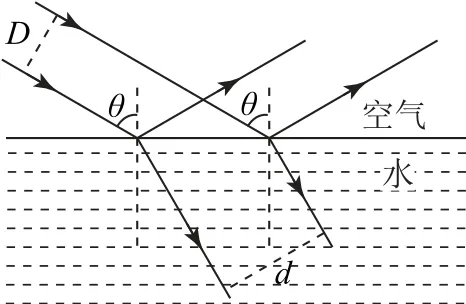
图9
(1)水的折射率n;
(2)两条折射光线之间的距离d.
解析
(1)设折射角为r,根据几何关系可得r=90°-θ,根据折射定律可得n=联立可得n=tanθ.
(2)设两条距离为D的平行光线射到水面上两点之间的距离为s,如图10所示.由几何关系可得D=scosθ,d=ssinθ,联立解得d=Dtanθ.
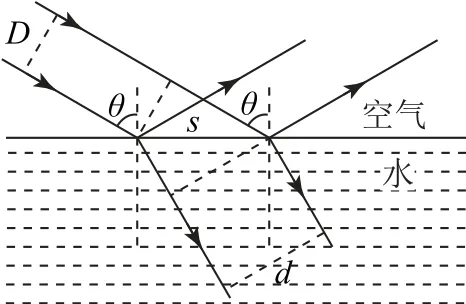
图10
【关键点拨】从光路图中找出两条折射光线之间的距离d与两条入射光线之间的距离D的关系,是正确解题的关键.
(完)
