钢-混组合梁斜拉桥极限承载能力分析
2023-02-27陈星CHENXing张皓ZHANGHao矣志勇YIZhiyong夏支贤XIAZhixian
陈星CHEN Xing;张皓ZHANG Hao;矣志勇YI Zhi-yong;夏支贤XIA Zhi-xian
(云南省交通规划设计研究院有限公司,昆明 650041)
0 引言
组合梁斜拉桥结构充分利用钢和混凝土两种材料的优势,便于工厂化生产,施工方便,越来越多的在工程中运用[1]。组合梁斜拉桥一般桥面较宽,桥塔高耸,整体结构纤细。随着桥梁跨度的增大,桥梁的稳定问题日益凸显。因此,在进行工程设计及施工运营时,分析结构的稳定承载能力,进行合理的安全评估非常重要。
结构在荷载作用下由于强度问题引起整体刚度下降,导致结构失稳。可见,结构的第二类稳定问题实质上是整体结构的极限承载能力问题[2-3]。针对斜拉桥结构的第二类稳定问题,众多学者开展了相关研究。刘永健[4]对众多我国已建成的斜拉桥主梁的弹塑性稳定性进行统计,部分斜拉桥的主梁弹塑性安全系数小于2.5,但仍正常运营,表明混凝土主梁和钢主梁的弹塑性安全系数分别不小于2.5 和1.75 是合理的。同时表明斜拉桥结构满足弹性稳定安全系数,并不一定满足弹塑性稳定安全系数。张喜刚[5]对苏通长江大桥进行稳定分析表明,斜拉桥在极限加载过程中,部分斜拉索率先达到单根构件的极限承载力,而后主塔与横梁交界处混凝土压碎。在到达极限承载力前,钢箱梁局部屈服。全桥的弹塑性失稳路径为:拉索→主塔→主梁。白植舟[6]对一座大跨径混合梁斜拉桥(边跨为预应力混凝土箱梁、中跨为钢桁梁)进行极限承载力研究,结果显示桥塔附近钢桁梁首先受压屈服,而后部分斜拉索屈服,结构的破坏机理表现为斜拉索屈服后钢桁梁塑性区不断扩大,最终结构失效。徐金勇[7]采用空间分析程序对一座主跨480m的双塔三跨混合梁斜拉桥进行弹塑性承载能力分析,表明极限荷载下,考虑材料非线性对斜拉桥主梁和桥塔的轴力无影响,但弯矩的重分布比较明显。
计算组合梁的极限承载能力,对结构的失效路径进行分析,有利于评估构件的承载能力,发现结构的薄弱环节,为组合梁斜拉桥的设计、施工、运营提供参考。
1 工程背景及有限元模型建立
勐醒至江城至绿春高速公路李仙江特大桥为主跨420m 的组合梁斜拉桥,全桥布置62.4m+127.6m+420m+127.6m+62.4m,为双塔半漂浮体系,主塔高250m,其立面布置图如图1 所示。索塔处设置竖向支座和横向抗风支座,竖向支座为双向活动支座,纵向设置弹性-阻尼复合式阻尼器。辅助墩、过渡墩设置竖向拉压支座,支座为单向活动支座,活动方向为顺桥向。
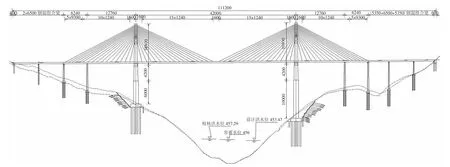
图1 组合梁斜拉桥立面布置图
该桥为双向四车道高速公路特大桥,设计车速80km/h,桥面净宽29m,组合梁在斜拉索锚固处高3.5m,其中钢主梁高3m,混凝土桥面板厚0.5m,主梁断面采用双边工字型截面,横桥向两道钢主梁中心间距26.5m。其标准横断面见图2。主桥斜拉索采用1770MPa 镀锌平行钢丝斜拉索,全桥共计4×16×2=128 根斜拉索,斜拉布置采用平行索面布置。
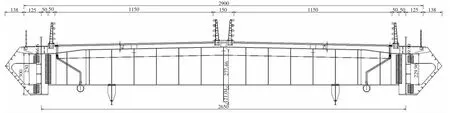
图2 组合梁标准横断面
绿春岸索塔总高250m,其中塔墩高100m,下塔柱高42m,中塔柱高55m,上塔柱高53m。索塔采用花瓶形构造,塔墩为单箱三室矩形截面,塔柱及横梁为单箱单室矩形截面;塔墩、塔柱、承台及桩基为钢筋混凝土构件(上塔柱索塔锚固区根据受力需要设置环向预应力钢绞线);上下横梁均为预应力混凝土构件。
本文采用ANSYS 建立组合梁斜拉桥的空间单梁鱼骨架模型,主梁及索塔采用beam188 单元模拟,斜拉桥采用LINK8 单元模拟。支座采用combin14 弹簧单元模拟,通过实常数设置支座刚度,塔底和墩底固结。全桥有限元模型如图3 所示。
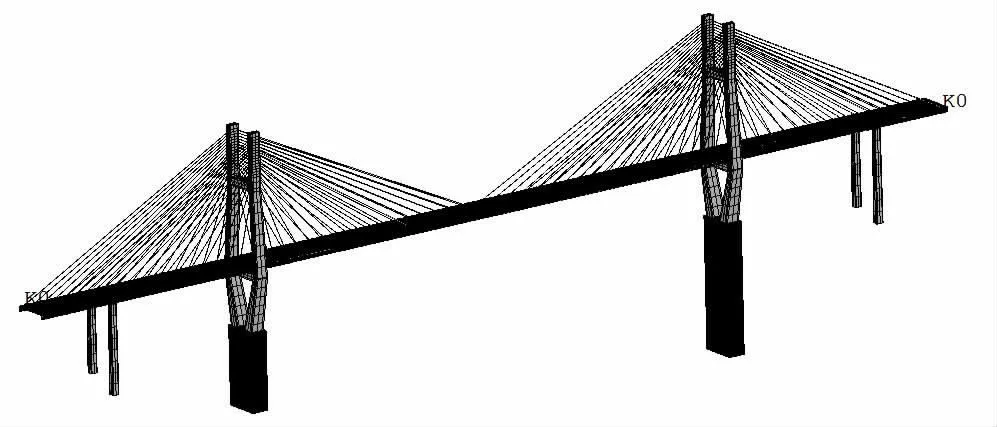
图3 组合梁斜拉桥有限元模型
钢主梁采用Q370qD 钢材,本构关系采用理想弹塑性模型,弹性模量Es=210GPa,屈服应力370MPa。斜拉索本构关系也采用理想弹塑性模型。主塔采用C55 混凝土,桥面板采用C60 混凝土,混凝土本构关系简化为分段折线模型,混凝土极限抗压强度取轴心抗压强度,混凝土比例极限对应的抗压强度取40%的轴心抗压强度[8]。
2 结构稳定性评价指标
结构的第二类稳定问题实质上是整体结构的极限承载能力问题。结构考虑几何非线性和材料非线性,并考虑结构存在的初始缺陷,则结构的平衡方程可表示为:
K0——结构弹塑性刚度矩阵;KL——结构大位移刚度矩阵;Kδ——结构初应力刚度矩阵;U——节点位移矩阵;P——等效节点荷载矩阵。有限元计算时不断计入结构的材料非线性和几何非线性,每迭代一步都对应不同的结构刚度矩阵。因此采用荷载增量法迭代计算,所得到的荷载—位移曲线的上限即为整体结构的极限承载力,此时结构所受荷载即为结构的极限荷载。
3 运营阶段的极限承载能力分析
3.1 不同活载加载方式下结构承载力分析
运营阶段分析时考虑活载布置差异对承载能力的影响,着重讨论以下六种加载方式。
①恒载+纵向运营风+全桥满布活载;
②恒载+纵向运营风+跨中满布活载;
③恒载+纵向百年风;
④恒载+横向运营风+全桥满布活载;
⑤恒载+横向运营风+跨中满布活载;
⑥恒载+横向百年风。
计算出不同工况下斜拉桥的全桥稳定系数如表1 所示,同时计算得出斜拉桥各组成构件开始破坏时的稳定系数如表2 所示。

表1 不同加载工况下运营阶段第二类稳定系数

表2 不同加载工况下各构件初始破坏时的第二类稳定系数
对斜拉桥结构进行弹性稳定性计算可以发现,结构的一阶失稳模态为纵飘失稳。索塔横向相当于框架受力,相比于纵向刚度,结构横向刚度更大,因此斜拉桥失稳模态一般为纵向挠曲失稳。通过表1 的计算结果可以发现,恒载+纵向百年风工况下,全桥的第二类稳定系数最小,最小值为2.60。对比纵向风荷载和横向风荷载工况,纵向风作用下结构的稳定系数更小,说明纵向风荷载对整体结构的稳定承载能力更为不利。因此,进行组合梁斜拉桥弹塑性稳定分析时,建议采用恒载+纵向运营风+活载、恒载+纵向百年风的加载方式进行计算。
以工况①恒载+纵向运营风+全桥满布荷载为例,分析成桥阶段结构的破坏过程。提取索塔塔顶的纵向位移与第二类稳定系数的发展规律,绘制得到第二类稳定分析典型的荷载—位移曲线,如图4 所示。
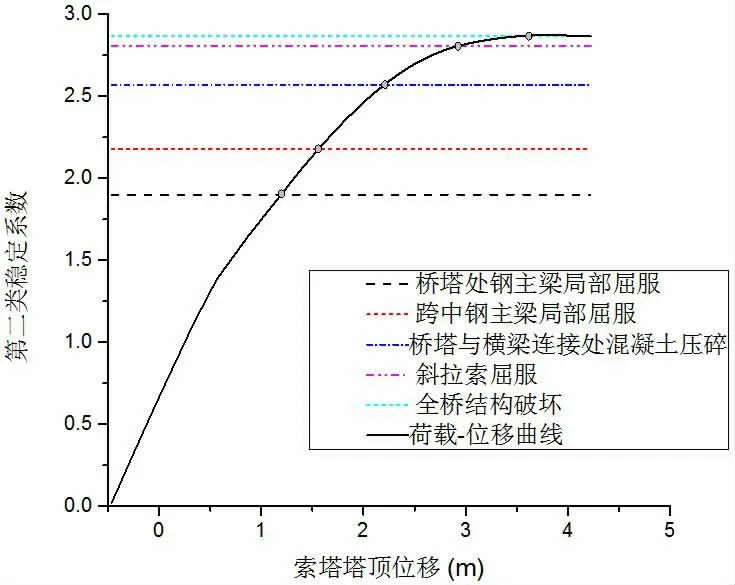
图4 索塔塔顶荷载—位移曲线
当结构的稳定系数达到1.90 时,近塔处钢主梁首先达到屈服应力370MPa。随着荷载的增加,稳定系数达到2.18 时,主梁跨中位移增大至1.56m,钢主梁下缘局部受拉屈服。荷载进一步增大,当稳定系数达到2.57 时,桥塔与横梁交接处混凝土达到轴心抗压强度,桥塔局部混凝土压碎。当结构稳定系数达到2.81 时,斜拉索Z9 屈服断裂。此后,稳定系数达到2.87 时,主塔与横梁交界处混凝土压碎区域不断扩大,形成几何可变体系,斜拉桥结构整体破坏。
3.2 结构构件承载能力评估
以工况①全桥满布荷载为例,依次分析组合梁斜拉桥主要构件在加载破坏过程中的受力、变形情况,并对各结构构件的承载能力进行评估(K 为结构的第二类稳定系数取值)。
3.2.1 斜拉索
加载过程中,各斜拉索的应力逐渐增大,直至部分斜拉索屈服断裂。K=1 时,斜拉索的应力水平为442~617MPa,最大拉索应力617MPa,强度安全系数2.87,大于规范规定斜拉索安全系数2.5 的要求。K=2 时,斜拉索的应力水平为615~1255MPa,平均索拉力935MPa,拉索的应力水平大幅提高。K=2.5 时,斜拉索的应力水平为752~1389MPa,平均索拉力1070MPa。K=2.81 时,Z9 斜拉索达到屈服应力,拉索断裂,其余拉索平均拉索应力1305MPa。
荷载加载到K=2.5 时,Z9 斜拉索的的应力为1389MPa,相比于K=1 时斜拉索应力617MPa,斜拉索的应力仅提高为原来的2.25 倍。其差别为结构稳定性分析时的非线性因素引起的,而斜拉索的强度安全系数是一种线性叠加效应,未考虑结构非线性的影响。
3.2.2 桥塔
索塔与横梁交界处应力较为集中,为结构的薄弱环节。加载后,桥塔逐渐向跨中方向偏移,跨中一侧混凝土承受巨大的轴力和弯矩,压应力较大。K=2.57 时,主梁与横梁交界处混凝土的最大主压应力达到混凝土的轴心抗压强度35.5MPa,结构局部混凝土压碎。随着荷载的增加,压碎区域逐渐向上塔和下塔柱发展,桥塔截面混凝土破坏发展明显。当K=2.87 时,桥塔区域混凝土大面积压碎。如图5 所示,桥塔跨中侧(背风侧)主压应力明显高于迎风侧,可知索塔的主要变形为纵向挠曲。为降低交界面处的应力,设计时应合理配置钢筋。考虑提高结构的极限承载力时,可以在此处设置合理的加固措施。
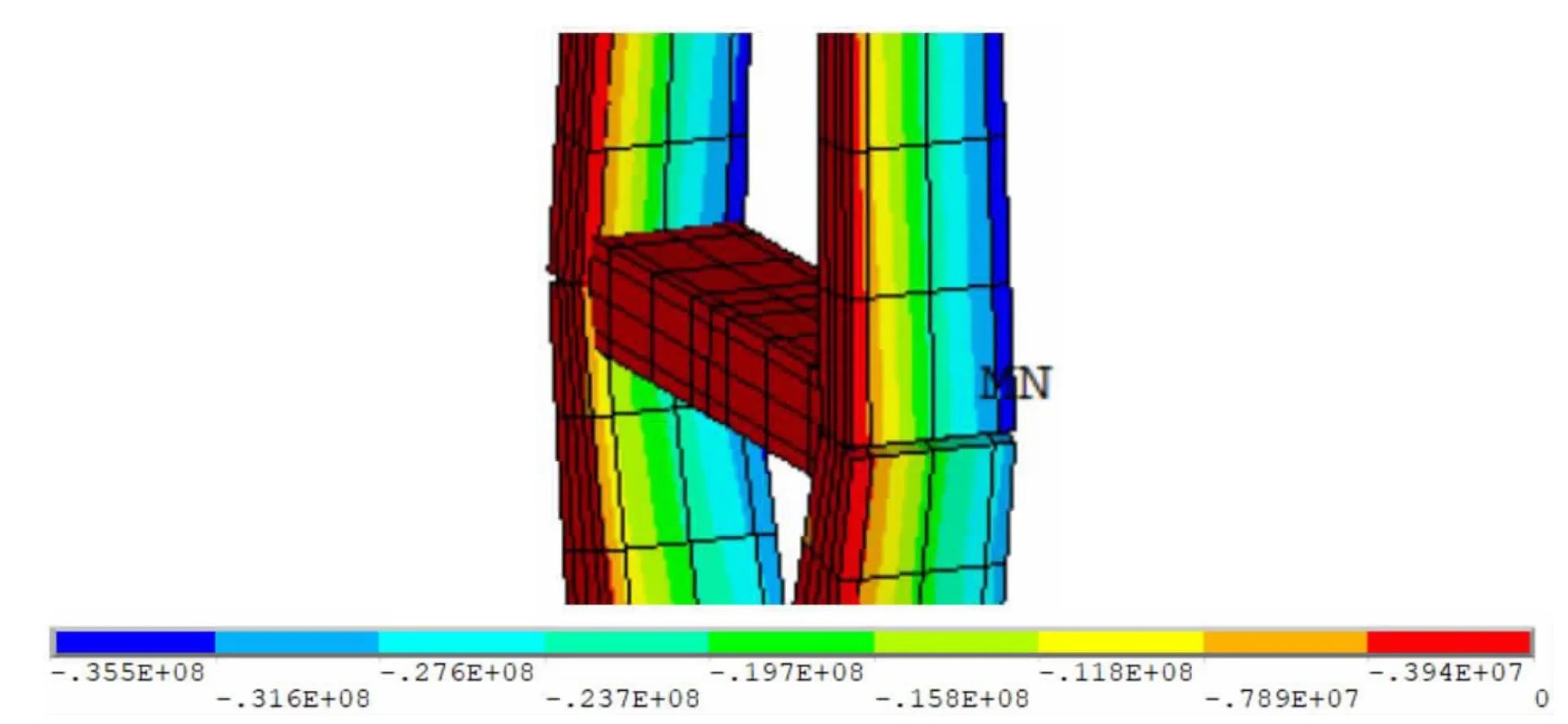
图5 索塔与横梁交界处混凝土主压应力(Pa)
3.2.3 主梁
主梁两侧工字钢承受斜拉索的巨大轴力,K=1.9 时,桥塔处主梁达到屈服应力370MPa,局部区域开始屈服。说明工字型钢主梁的轴向承载能力较弱,但在达到极限承载力前,钢主梁有很长的塑性发展空间,其对结构的整体稳定性不起控制作用。结构破坏前,钢主梁局部区域大面积屈服。结构在达到极限荷载前,桥塔处的部分混凝土桥面板压溃,结构在整体破坏前有明显的征兆。
4 结构失稳路径分析
主梁结构的强度对于斜拉桥全桥的破坏路径有显著的影响。本文计算的斜拉桥为双工字型组合梁斜拉桥,主梁结构强度相较于钢箱梁[9]结构显著降低,轴向抗压能力有限,加载后钢主梁结构首先屈服。本文组合梁斜拉桥全桥破坏路径为:主梁→主塔→拉索→整体结构破坏。在进行斜拉桥设计时,应事前评估组成斜拉桥的各构件的承载能力,保证斜拉桥的破坏路径合理、结构破坏过程有明显的延性。
5 结论
针对双工字型组合梁斜拉桥,运用有限元软件ANSYS 对运营阶段典型工况下的极限承载力进行计算,结论如下:
①针对运营阶段六种典型加载方式,计算得出工况四(恒载+纵向百年风)作用下结构的稳定系数更小。对比纵向风荷载和横向风荷载工况,纵向风作用对结构的承载能力更不利。一般进行斜拉桥的稳定计算时,可仅考虑纵向风与其它荷载组合的工况。
②斜拉桥结构达到极限承载承载能力过程中,结构发生了明显的非线性失稳破坏。索塔构件失稳时出现了典型的压弯破坏,索塔与横梁交界处混凝土压碎区域不断扩大,导致斜拉桥全桥失稳破坏。
③对全桥进行承载能力分析,得出组合梁斜拉桥全桥破坏路径为:主梁→主塔→拉索→整体结构破坏。双工字型组合梁斜拉桥主梁轴向抗压强度较弱,桥塔附近钢主梁最先屈服。
