基于线性方程组整体消元过程的行列式知识构建

王永革,马 健

(北京航空航天大学 数学科学学院,北京 102206)

0 引言

在行列式知识体系里,有几个核心概念常常成为学生学习中的疑点,同时也是教学的难点,因此被多数教师反复探讨[1]。这些疑难点主要包括:①行列式定义。应该怎样定义行列式,为什么这样定义行列式,为什么要引入逆序数。目前的文献给出了行列式定义的3种方法,但每种方法都有其“缺憾”之处[2-3]。②行列式展开定理。为什么会提出展开定理,展开定理为什么成立,为什么要引入代数余子式,目前的文献多是从低维类比,探讨定理的证明方法,对定理如何提出为何提出涉及较少[4]。③克莱姆法则。克莱姆法则怎么来的,为什么会成立等,文献涉及较少[5]。

反映在教学中,一方面这些疑难点的引入大多较为牵强,甚至常常让学生感到突兀;另一方面,这些疑难点常被作为背景较为孤立的知识,没有作为一个有机的整体呈现。为此,本文从线性代数最基本的背景——线性方程组出发[6],首先探索线性方程组整体消元求解的方法,其次将各疑难点作为消元过程中陆续出现的结果,自然引入相关概念,揭示上述疑难点直观意义的同时,也让学生较容易的理解这些疑难点的含义及本质,理解其在统一背景中的内在联系。

1 线性方程组的整体消元求解

1.1 二元线性方程组消元求解

用消元法解二元线性方程组

保留未知数x1而消去未知数x2,将方程(A1)×a22+(A2)×(-a12),得

(a11a22-a21a12)x1=b1a22-b2a12。

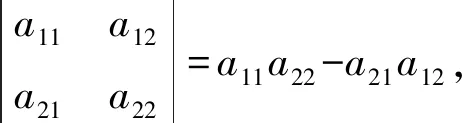
1.2 三元线性方程组整体消元求解及启示

用消元法解三元线性方程组

不失一般性,只保留未知数x1而消去其余所有未知数,即x2,x3,并将此消元方法称为整体消元。为此将方程(B1)×k1+(B2)×k2+(B3)×k3,得合并方程

(a11k1+a21k2+a31k3)x1+(a12k1+a22k2+a32k3)x2+(a13k1+a23k2+a33k3)x3=b1k1+b2k2+b3k3。

令a12k1+a22k2+a32k3=0,a13k1+a23k2+a33k3=0,得其中一解

将k1,k2,k3的该解带入,可同时消去x2,x3,只保留未知数x1,从而得到x1的解,同样的方法可以得到x2,x3的解。

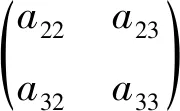
将方程(B2)、(B3)分别乘以上述各项后再相加。为消去x2,x3,如果这些项中a22a33的符号为正,则a12a33的符号需要为负,这样乘积为a12a22a33的两项符号相反,相加后未知数x2的系数才能为零;a13a22的符号也为负,相加后才可以消去未知数x3的对应系数项a13a22a33。同样的分析可知,a13a32的符号为正,a23a32的符号为负,a12a23的符号为正。

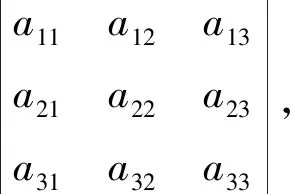
1.3 n元线性方程组整体消元求解过程

类比三元线性方程组的整体消元过程,对n元方程组进行消元求解。

1.3.1 整体消元中方程所乘项因子的确定

对n元线性方程组

采用整体消元。不失一般性,只保留未知数x1而消去其他未知数x2,x3,…,xn。类比三元线性方程组的整体消元可知,需要每一个方程乘以其余方程中x2,x3,…,xn(即除x1外)的系数矩阵的不同行不同列的乘积项,共(n-1)!项,即需要对方程组作如下消元运算

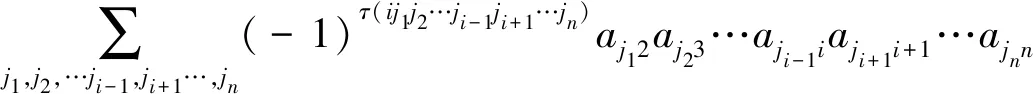
这样未知数x2,x3,…,xn中每个未知数的系数共有n×(n-1)!=n!个乘积项,且乘积项中总有两项绝对值相同,这两项可以通过设计相反的符号使得相加为零,以实现整体消去x2,x3,…,xn的目的。如运算后x2的系数为

消去x2需要 (-1)τ(pqj1j2…jp-1jp+1…jq-1jq+1…jn)+(-1)τ(qpj1j2…jp-1jp+1…jq-1jq+1…jn)=0。此时x1的系数为

再分别考虑保留未知数xp(p=2,3,…,n),消去x1,x2,…xp-1,xp+1,…,xn时xq(q≠p)的系数,可知对∀q≠p,有(-1)τ(j1…jp…jq…jn)aj11…ajpq…ajqq…ajnn与(-1)τ(j1…jq…jp…jn)aj11…ajqq…ajpq…ajnn符号相反,故τ(j1…jp…jq…jn)与τ(j1…jq…jp…jn)奇偶性不同。

即若交换排列j1…jp…jq…jn中jp,jq的位置,得到新的排列j1…jq…jp…jn,则函数τ(j1…jp…jq…jn)与τ(j1…jq…jp…jn)的奇偶性将发生变化,且可以设定τ(123…n)为偶数。故任一排列j1…jp…jq…jn对应函数τ(j1…jp…jq…jn)的奇偶性,可以由j1…jp…jq…jn中元素交换到12…n时,交换次数的奇偶性确定。

1.3.2 整体消元中方程所乘项符号的确定

先考虑排列j1…jp…jq…jn中元素1的位置,不失一般性,设为j1…jp…1…jq…jn,将1依次与它前面的元素交换,交换的次数记为τ(1),其值为排在1前面且比1大的数字的个数,即由1产生的逆序数,交换后的排列为1j1…jp…jq…jn;再考虑元素2,不失一般性设为1j1…jp…2…jq…jn,将2依次与它前面的元素交换,交换的次数记为τ(2),其值为排在2前面且比2大的数字的个数,即由2产生的逆序数,交换后的排列为12j1…jp…jq…jn;再依次考虑元素3,4,…,n,分别再经过τ(3),τ(4),…,τ(n)次的交换,变换为排列123…n。这样共通过τ(1)+τ(2)+…+τ(n)次的交换,排列j1…jp…jq…jn变为123…n。

若τ(1)+τ(2)+…+τ(n)为偶,则通过偶数次交换,排列j1…jp…jq…jn变为123…n,即对应的乘积项(-1)τ(j1…p…q…jn)aj11…apip…aqiq…ajnn经过偶数次变号,结果为正,故其原值也为正,故τ(j1…jp…jq…jn)必为偶数;若τ(1)+τ(2)+…+τ(n)为奇,则通过奇数次对换,排列j1…jp…jq…jn变为123…n,即对应的乘积项(-1)τ(j1…p…q…jn)aj11…apip…aqiq…ajnn经过奇数次变号,结果为正,故其原值为负,故τ(j1…jp…jq…jn)必为奇数。即τ(j1…jp…jq…jn)与τ(1)+τ(2)+…+τ(n)的奇偶性总是保持一致。故可设τ(j1…jp…jq…jn)=τ(1)+τ(2)+…+τ(n),并将其定义为排列j1…jp…jq…jn的逆序数,则每个乘积项及其符号可表示为(-1)τ(j1j2…jn),aj11aj22…ajnn,其中τ(j1j2…jn)为排列j1j2…jn的逆序数。

1.3.3n元线性方程组的解

通过确定每个方程所乘项的因子和符号,实现只保留其中一个未知数而整体消去其他所有的未知数。不失一般性,设保留未知数x1,而整体消去x2,x3,…,xn,由前述分析可知,此时未知数x1的系数为

即方程组系数矩阵中所有不同行不同列元素乘积的代数和,其中乘积项aj11aj22…ajnn的符号为(-1)τ(j1j2…jn)。而每个方程等号右边的常数经过上述消元操作后,常数项为

……

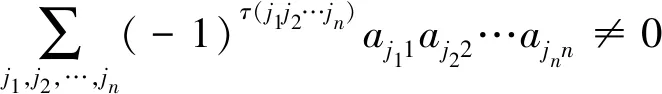
2 基于整体消元过程的行列式知识构建

上述n元线性方程组的整体消元过程,包含了行列式知识体系的主要疑难点,提供了这些概念产生的共同背景。基于该过程,可以较容易地理解这些疑难点的含义以及它们之间的内在联系。

2.1 行列式定义

此定义即线性代数教材中的代数和定义[7],从方程组整体消元过程可以很容易理解,为什么行列式要定义为不同行不同列的项的代数和。目前大多数教材按该方式定义行列式时,通常是在归纳二阶、三阶行列式为不同行不同列的乘积项代数和这一特点后,直接以一句话“将这一结果推广到n阶”,随后给出n阶行列式的上述定义,但这样引入的定义给学生留下诸多疑问,如二阶、三阶行列式为什么有这样的特点,是否可以推广到n阶,为什么要推广到n阶等,这些疑问在上述线性方程组整体消元过程中都可以得到清晰自然的解释。

2.2 逆序数

在行列式定义中,逆序数往往让学生感到突兀,学生不理解行列式与逆序数有什么联系,不理解为何会想到用逆序数来定义行列式。

由消元过程可以看到,若只保留未知数x1,而整体消去其他的未知数x2,x3,…,xn,乘积项(-1)τ(j1…jp…jq…jn)aj11…ajpq…ajqq…ajnn与(-1)τ(j1…jq…jp…jn)aj11…ajqq…ajpq…ajnn符号须相反,即τ(j1…jp…jq…jn)与τ(j1…jq…jp…jn)奇偶性不同。故若交换排列j1…jp…jq…jn中jp,jq的位置,得到新的排列j1…jq…jp…jn,则函数τ(j1…jp…jq…jn)与τ(j1…jq…jp…jn)的奇偶性将发生变化,另外假设τ(123…n)为偶数,由前述分析知可设τ(j1…jp…jq…jn)=τ(1)+τ(2)+…+τ(n),其中τ(i),i=1,2,…,n为排列中在i前面且比i大的数字的个数,此即为排列的逆序数定义。

即排列的逆序数是为消去未知数而设计的一种确定符号的方法。利用排列的逆序数的奇偶性对应每一个不同行不同列乘积项的正负,可以整体消去除保留的未知数外的其他所有未知数。事实上,由上述确定符号的过程可以知道,逆序数不是唯一的确定符号方法,只要满足交换排列中两个数的顺序,该排列对应的乘积项符号就能改变的任何函数都可以,但逆序数是一种规律简单使用方便的函数,于是通常用逆序数确定乘积项的符号。

有了上述行列式整体消元的背景,学生就不难理解为什么要学习逆序数以及行列式定义中为什么要使用逆序数了。

2.3 代数余子式

在保留x1消去其他未知数的整体消元过程中,将第i个方程所乘的项,即ai1所乘的项

定义为元素ai1的代数余子式。为形式上更直观清晰,可将该项变形为

其中Mi1为系数矩阵去掉第一列和第i行之后的元素组成的行列式,称为ai1的余子式。

同样,只保留xp消去其他未知数的整体消元过程中,第i个方程所乘的项,即aip所乘的项

称为aip的代数余子式,其中τ(j1…ji-1ji+1…i…jn)中的排列,i排在第p个位置。为形式上简单直观,可变形为

称为aip的代数余子式,其中Mip为系数矩阵去掉第p列和第i行之后的元素组成的行列式,称为aip的余子式。

可以看出,aip的代数余子式是在只保留xp而消去其他未知数的整体消元过程中,第i个方程所要乘的项,这样在线性方程组整体消元的背景中,很容易地理解了为什么要引入代数余子式这一概念。

2.4 行列式展开定理

在保留x1消去其他未知数的整体消元过程中,其他未知数的系数都将合并为零,如x2的系数

结果为零。由前面关于代数余子式的讨论可知,该式等于a12×A11+a22×A21+…+an2×An1,即系数矩阵中第二列的元素分别乘以同一行中第一列元素的代数余子式之和,结果为零。

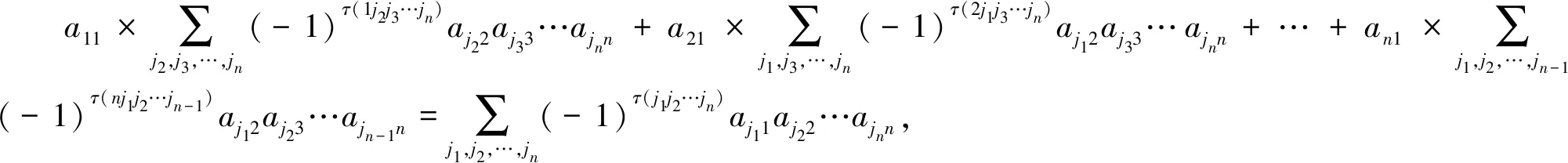
同样的分析可知,保留xp消去其他未知数的整体消元过程中,xi(i≠p)的系数a1i×A1p+a2i×A2p+…+ani×Anp=0,此即第i列的元素乘以第p列对应元素的代数余子式之和为零。xp的系数a1p×A1p+a2p×A2p+…+anp×Anp=D,即第p列的元素分别乘以该元素的代数余子式之和,为系数矩阵行列式的值,此即行列式按列展开的定理。

由上分析可知,行列式的展开定理,其实是在线性方程组整体消元中,保留的未知数的系数,按前述行列式定义,该系数自然为系数矩阵行列式的值。而其他消去的未知数的系数为零,其实是某一列乘以另外一列的代数余子式之和为零。这样在线性方程组整体消元背景下,行列式展开定理成了一个自然成立的结论,容易理解甚至无需证明。

2.5 克莱姆法则

在保留x1消去其他未知数的整体消元过程中,保留的未知数x1的系数,即行列式的值D,而方程组等号右边常数项进行相应的变形后,结果是

由上可知,线性方程组整体消元求解的结果即为克莱姆法则,故在此背景下,克莱姆法则也自然成立。

3 总结及结论

对n元线性方程组给出了一个整体消元求解的方法,基于该消元求解过程,展示了行列式定义、逆序数、代数余子式、行列式展开定理及克莱姆法则等行列式核心概念,从一个共同的背景中构建了行列式的主要知识,阐释了行列式的主要疑难点。

线性方程组整体消元过程表明,行列式主要知识和疑难点,都是在整体消元中某一步骤或操作中需要用到的对象,都是方程组消元求解中某一方面的结果呈现。该过程也揭示了这些概念之间内在的联系,它们存在于求解过程的不同阶段或不同角度,共同构成了线性方程组的整体消元求解场景。