扰动的Ostrowski型不等式的量子模拟

时统业

(海军指挥学院,江苏 南京 211800)

0 引言

著名的Ostrowski不等式[1]是

其中f是[a,b]上的可微函数,对任意x∈[a,b]有|f′(x)|≤M。

有关Ostrowski不等式的变式、推广和加强,可见文献[2-9]及其引证文献。针对二阶导数有界的二次可微函数,CERONE P等[3]利用恒等式

建立了带有扰动的Ostrowski型不等式,

(1)

DRAGOMIR S S等[4]利用恒等式

证明了带有扰动的Ostrowski型不等式,

(2)

其中f′在[a,b]上绝对连续且f″在(a,b)上有界。

TARIBOON J等[10]引入了q导数和q积分的概念,BERMUDO S等[11]引入qb导数和qb积分的概念。

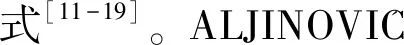
定义1[10,15]设f在[a,b]上连续,q∈(0,1),则定义f在点x∈(a,b]处的q导数为

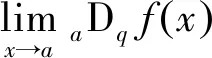
如果f在[a,b]上每个点处的q导数都存在,则称f是[a,b]上的q可微函数。

定义2[10,15]设f在[a,b]上连续,t∈[a,b],q∈(0,1),则定义f在[a,t]上的q积分为

定义1和定义2分别是[0,b]上的q-Jackson导数和q-Jackson积分[20]概念的推广。

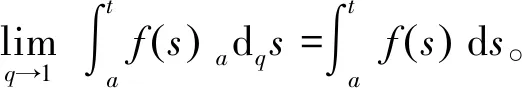
定义3[10]设f在[a,b]上连续,q∈(0,1),对于任意x∈(a,b],称

设f,g在[a,b]上q可微,x∈[a,b],则有q积分的分部积分公式[10]

定义4[11]设f在[a,b]上函数,q∈(0,1),则定义f在点x∈[a,b)处的qb导数为

如果f在[a,b]上每个点处的qb导数都存在,则称f是[a,b]上的qb可微函数。

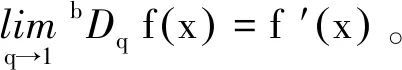
定义5设f在[a,b]上函数,q∈(0,1),对于任意x∈[a,b),称

定义6[11]设f在[a,b]上函数,t∈[a,b],q∈(0,1),则定义f在[t,b]上的qb积分为

设f和g是[a,b]上两个qb可微函数,x∈[a,b],则有qb积分的分部积分公式

为方便起见,记

引理1设f在[a,b]上q可微,则对任意x∈[a,b]有

(3)

证明由q积分的分部积分公式得

(4)

综合式(4)和式(5)得

(6)

类似地,利用qb积分的分部积分法可得

(7)

将式(6)与式(7)相加,则式(3)得证。

引理2设f在[a,b]上二阶q可微,则对任意x∈[a,b]有

证明利用q积分的分部积分公式和qb积分的分部积分公式可证(略)。

1 主要结果

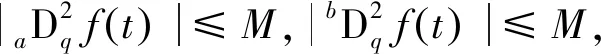
(8)

证明令

由引理1有

|I|≤MK。

(9)

先估计K1。由q积分的定义有

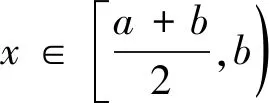
其中

下面估计K2。由q积分和qb积分的定义有

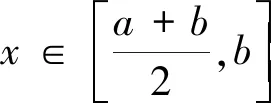
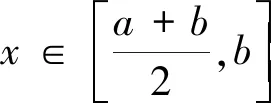
所以,对任意x∈[a,b],有

(10)

最后,综合式(9)和式(10)证得式(8)成立。

注1在定理1中令q→1,则由式(8)得到式(2)。

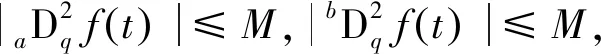
(11)

其中U=(x-a)2(aDqf(x)-aDqf(a))+(b-x)2(bDqf(b)-bDqf(x))。

证明对任意的常数ε∈[0,1],有

(12)

为求ψ(ε)的最小值,求导得ψ′(ε)=3ε(ε-ε1),因为

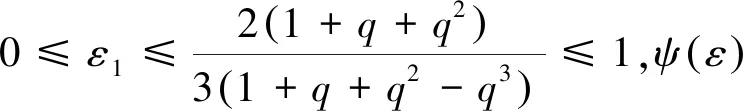
再利用引理2,则式(11)的右边不等式得证。对(-f)使用已证结果,则(11)的左边不等式得证。

推论1设条件同定理2,则对任意x∈[a,b],有

推论2设f在[a,b]上二次可微,且f″在(a,b)上有界,则对任意x∈[a,b]有

证明在推论1中令q→1,即可得证。

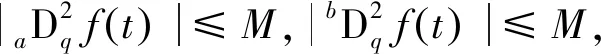
(13)

其中

证明对任意常数ε∈[0,1],有

(14)

其中

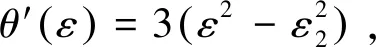
所以有

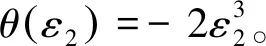
再利用引理2,则式(13)的右边不等式得证。对(-f)使用已证结果,则式(13)的左边不等式得证。

推论3设条件同定理3,则对任意x∈[a,b]有

推论4设f在[a,b]上二次可微,且f″在(a,b)上有界,则对任意x∈[a,b]有

证明在推论3中令q→1即可得证。