燃气涡轮发动机关键部件疲劳小裂纹研究进展
2023-02-24赵高乐齐红宇李少林杨晓光石多奇
赵高乐 齐红宇 李少林 杨晓光 石多奇
北京航空航天大学 能源与动力工程学院,北京 100191
航空发动机结构强度北京市重点实验室,北京 100191
1 引言
随着先进燃气涡轮发动机性能不断地提升,导致工作条件越来越恶劣和复杂,这对航空发动机部件结构强度提出了严峻挑战.其中,先进燃气涡轮发动机中的涡轮叶片和涡轮盘等关键部件所处服役环境最为苛刻.涡轮叶片和涡轮盘承受机械、气动等多场复杂交变载荷,这些载荷间存在强非线性,使得涡轮叶片和涡轮盘可能产生蠕变或持久、疲劳和蠕变-疲劳等机械损伤.其中,低周、高周、超高周和高低周复合等疲劳损伤模式显著地降低了涡轮叶片和涡轮盘的力学性能,制约了航空发动机安全运行和服役寿命.疲劳损伤过程主要由裂纹萌生和裂纹扩展两个独立的阶段组成,且裂纹萌生阶段占据了大部分的疲劳寿命.由于裂纹萌生过程基本处于微观尺度范围,故针对疲劳的研究主要集中在长裂纹的扩展方面.然而,随着检测手段的发展,人们在更加微观的尺度下发现了不同于长裂纹扩展规律的小裂纹效应.因此,为保障先进燃气涡轮发动机的安全运行,避免重大的事故发生和巨大的经济损失,复杂载荷作用下的疲劳小裂纹扩展问题研究也成为了前沿发展方向之一.
小裂纹的相关研究最早可追溯到20 世纪70 年代.Pearosn (1975)在1975 年首次提出“小裂纹”的概念,并指出疲劳小裂纹快速扩展的特性.在ASTM (E1823) 标准中描述了“短裂纹”和“小裂纹”两个术语: 当裂纹只有一个物理尺寸 (通常是贯穿裂纹的长度)且很小时,定义为“短裂纹”;而小裂纹被认为是与相关的微观结构尺度、连续介质力学尺度或物理尺寸尺度相比,在三维(长度和深度) 中都较小的裂纹.尽管定义上存在差别,但鉴于两者规律相似,许多研究中也没有严格区分,因此,在本文中都使用“小裂纹”一词来统一代表小裂纹和短裂纹.ASTM (E647 13a)从三个角度定义小裂纹效应: (1) 裂纹长度小于微观结构尺寸;(2) 与局部塑性尺度相比裂纹长度较小;(3) 物理尺寸较小,即裂纹长度小于0.5~ 1 mm.值得注意的是,定义小裂纹的具体物理尺寸随特定材料、几何结构和所需载荷的不同而不同.
疲劳小裂纹的形成和扩展是疲劳裂纹萌生阶段的重要部分.低周疲劳 (LCF) 和高周疲劳(HCF) 的裂纹倾向于在表面缺陷(Hu et al.2019)或持久滑移带(Zheng et al.2022)处萌生.对于超高周疲劳 (VHCF),裂纹更有可能从内部缺陷成核(Qin et al.2023b).在高温环境中,氧化和热腐蚀导致材料表面发生明显劣化,从而影响疲劳损伤演化过程.对于LCF 和HCF,试件表面形成的氧化膜呈脆性,在较大的循环载荷作用下容易开裂或脱落,导致多条新裂纹面的形成(Han et al.2020).而VHCF 过程中施加的应力相对较小,氧化膜不易发生破坏,从而起到了一定的保护作用(Li et al.2023),故材料的内部微观组织更容易受到温度的影响(Hu et al.2022).相对于氧化,热腐蚀造成合金表面更为严重的损伤,应力集中效应导致疲劳裂纹从表面腐蚀缺陷 (腐蚀层、腐蚀坑) 处引发并扩展(Mahobia et al.2014,Zhao et al.2021,Behvar &Haghshenas 2023).
国内外疲劳断裂界学者(Piascik &Willard 1996,Piascik et al.1994,El Haddad et al.1979,Haddad et al.1979)对小裂纹的扩展行为以及疲劳全寿命预测的可行性进行了系统且深入的研究,主要得出了以下结论: (1) 在相同的名义应力强度因子范围ΔK下小裂纹的扩展速率高于长裂纹,且在低于长裂纹扩展门槛值ΔKth的情况下小裂纹仍能扩展,即所谓的“小裂纹效应”;(2) 材料的微观特征成为小裂纹在扩展过程中的障碍,导致其速率发生波动;(3) 有研究指出铝合金的疲劳寿命绝大部分消耗在小裂纹阶段,故对小裂纹扩展规律的研究就显得十分必要;(4) 影响小裂纹行为的一个力学因素是塑性区尺寸可能与裂纹尺寸相当,这造成线弹性断裂力学理论的失效,故将长裂纹扩展分析方法直接向小裂纹阶段延伸将会导致错误的寿命估计.因此,将小裂纹定义为不满足线弹性断裂力学约束条件的裂纹(洪友士和方飚 1993).另外,也有学者以实际尺寸来区分小裂纹效应,如 Miller (1993a,1991)认为长度尺寸小于0.5 mm 的裂纹为小裂纹,大于0.5~ 1 mm 的裂纹为长裂纹.
此外,Kitagawa-Takahashi 图不仅可以体现疲劳小裂纹扩展行为,还可以利用裂纹或等效缺陷尺寸来估算疲劳强度.Kitagawa-Takahashi 图中,疲劳数据用两条线来描述,其中一条线代表无缺陷材料的疲劳极限,另一条线则代表长裂纹扩展门槛值范围ΔKth(Kitagawa &Takahashi 1976).当施加的应力范围Δσ低于无缺陷材料疲劳极限Δσe或满足应力低于含缺陷/裂纹合金的疲劳极限这一条件时,部件被视为安全.随后,El-Haddad 提出了这一概念的修正理论(El Haddad et al.1979),该模型显示了从长裂纹门槛值到疲劳强度的平滑过渡.因此,如果施加的应力范围Δσ并且相应的缺陷尺寸位于El-Haddad 修正曲线之下,代表部件安全.通常a0表示为El-Haddad 虚拟的固有裂纹长度.
当小裂纹扩展到一定长度时则进入了长裂纹的扩展阶段.由于在发现小裂纹之前已将断裂力学应用于裂纹扩展阶段且取得了较大的成功,故早期的学者试图在线弹性断裂力学的框架下采用适用于长裂纹扩展的K理论来描述裂纹尖端弹塑性应力应变场强度参量.当前,在工程上仍有许多模型直接采用线弹性断裂力学参数或通过某些修正来描述小裂纹的扩展,从而建立工程应用判据.另一方面,也有相关的疲劳设计是从避免裂纹萌生的观点出发来研究小裂纹扩展行为的.虽然将断裂力学应用于裂纹扩展阶段取得了较大的成功,但由于小裂纹相较于长裂纹扩展的差异性,使得基于线弹性断裂力学理论模型不能直接用于小裂纹扩展寿命的分析预测(Hudak Jr 1981).即使在裂纹扩展驱动力中考虑了塑性区效应,也无法完全适用于小裂纹扩展阶段.因此,需要在大范围屈服的条件下得到能定量描述裂纹尖端区域应力应变场强度的参量,以便能用理论建立小裂纹扩展参量与其几何尺寸特性、载荷之间的关系,最后建立适用于小裂纹扩展的工程应用判据.
由于断裂参量K不能直接有效地描述小裂纹和长裂纹之间裂纹尖端行为的差异,故当前的研究人员试图使用适用于弹塑性理论下的裂纹扩展驱动力参量,包括有效J 积分(Döring et al.2006)、应变能密度(Sih 2009)、剪切应变范围(Miller 1993b)以及循环CTOD (Shyam et al.2005)来替代线弹性断裂力学参量.然而,这些驱动力参量需要依靠相应的试验来确定,使得它们的应用受到了限制.虽然人们在发展疲劳寿命的计算方法上进行了大量的研究工作,在将断裂力学理论应用于疲劳寿命分析,建立适合于疲劳裂纹形成和扩展全过程的寿命计算模型中取得了一定的进展.但是疲劳寿命的预测问题并没有得到较好的处理办法,这方面的工作还有待于深入探讨.因此,对疲劳小裂纹的扩展特性进行深入的分析,在裂纹扩展模型中考虑到小裂纹的影响因素,将断裂力学理论用于疲劳全过程,发展疲劳全寿命模型是一项有着重要理论意义及工程应用价值的工作.
本文围绕疲劳断裂过程中小裂纹阶段的研究成果,论述了小裂纹扩展行为对燃气涡轮发动机关键部件服役寿命的重要性.首先,详细介绍了小裂纹的分类、特点并分析了其对整体寿命的影响;其次,基于燃气涡轮发动机热端部件常用的多晶和单晶合金阐述了疲劳小裂纹的萌生机制和扩展机理,并利用Kitagawa-Takahashi 图对疲劳小裂纹和腐蚀疲劳小裂纹行为进行了论述;再次,系统综述了当前的疲劳小裂纹扩展模型;最后,针对当前先进燃气涡轮发动机服役环境的恶劣性,描述了腐蚀环境下的疲劳小裂纹扩展行为以及相关模型.
2 疲劳小裂纹的重要性
2.1 小裂纹扩展的分类及其特点
当前研究(Tanaka 2003)认为疲劳载荷导致结构件的失效,包括裂纹萌生、微观小裂纹的扩展、力学/物理小裂纹的扩展、长裂纹的扩展和最终断裂五个阶段,如图1 所示.值得注意的是,图中的裂纹尺寸为近似值且随材料类型的不同而发生变化.另有学者根据小裂纹的扩展规律将其分为微观组织小裂纹和物理小裂纹两个阶段(Hou et al.2020).而Suresh 和Ritchie (1984)及Gangloff (1985)将疲劳小裂纹分为微观小裂纹、力学小裂纹、物理小裂纹以及化学小裂纹四类.表1 列出了其对小裂纹的划分依据和特点,其中,a为裂纹长度,d表示晶粒或第二相等材料的特征微观组织尺寸,rp表示塑性区的大小.

表1 小裂纹的分类及特点

图1 不同尺度下的裂纹划分
微观小裂纹 (microstructurally small crack,MSC) 的尺寸与材料的微观结构特征数量级相当,范围从几微米到数百微米之间.由于其尺寸小于微组织结构,微观小裂纹扩展行为受到材料微观组织结构的强烈影响.事实上,MSC 扩展路径和速率是随机的,取决于裂纹尖端的微观结构特征(Lankford 1977,Tokaji et al.1986a).一旦裂纹尺寸超过数倍的晶粒尺寸,则不再认为是微观小裂纹.材料的微观组织不连续性造成MSC 阶段不适用于连续介质力学.
力学小裂纹 (mechanically small crack,MenSC) 的长度a小于局部塑性尺寸 (例如,嵌入缺口塑性区的小裂纹或长度与自身裂纹尖端塑性区相当的裂纹,超高强度材料通常小于0.01 mm,低强度材料通常在0.1~ 1 mm 的尺寸范围内).由于其裂纹尺寸小于塑性区域尺寸,也就是说MenSC 可能大部分长度都位于塑性区内,故在其扩展过程中受塑性诱发的闭合行为影响.
物理小裂纹 (physically small crack,PSC) 的长度约为微观结构尺度的5~ 10 倍(Owolabi &Whitworth 2014).虽然其扩展行为 (扩展路径和速率) 对材料自身的微观特征并不敏感,但其依旧在长裂纹门槛值以下并以高于长裂纹的扩展速率沿垂直于应力加载方向扩展.根据经验PSC小于平均晶粒尺寸的10 倍,其裂纹扩展路径大致垂直于载荷方向(Taylor &Knott 1981).PSC阶段虽然在扩展机制上逐渐趋向于长裂纹特征,但仍然存在着一些扩展速率上的波动和其他小裂纹特征.其尺寸在0.5~ 1 mm 的范围内,并未达到传统长裂纹的物理尺寸,故PSC 通常被认为是微观小裂纹到长裂纹的过渡阶段.由于许多初始缺陷在尺寸范围上属于PSC,因此PSC 通常是整个疲劳寿命的起点.
由于裂纹尖端显著的化学驱动力,化学小裂纹的生长速度明显高于长裂纹.而长裂纹的尺寸是微结构尺寸的10~ 20 倍以上(Owolabi &Whitworth 2014).长裂纹扩展至最终失效是损伤累积阶段,使用线性弹性断裂力学 (LEFM) 或弹塑性断裂力学 (EPFM) 可以很好地描述该阶段.事实上表1 中小裂纹的分类并不存在严格的界限,即同一状态下的小裂纹既可以满足微观组织小裂纹的特征,也可以满足力学/物理小裂纹的分类要求.但长裂纹与小裂纹的区别却十分清晰,根据小裂纹与长裂纹的不同以及断裂力学相似性准则的局限性,可以清楚地识别疲劳裂纹扩展过程中的小裂纹效应.小裂纹中各个阶段也并不能简单地只根据裂纹长度进行判别,阶段之间也有相互交集,这些分类设立的初衷是为了便于开展裂纹分析.
2.2 小裂纹行为对疲劳寿命的影响
众所周知,结构件的疲劳寿命组成涉及到裂纹萌生和裂纹扩展阶段,故小裂纹扩展阶段对整体疲劳寿命的贡献直接关系着对其的研究价值.如Cini 等 (2017) 通过比较裂纹扩展的不同阶段发现,裂纹成核和长裂纹扩展都不会影响结构件的整体寿命,而小裂纹状态会影响部件的总体寿命.由于小裂纹具有复杂和难以观测的特性,对其研究还存在一定的困难,尤其是在高温环境下工作的燃气涡轮发动机热端部件.倘若其仅占疲劳寿命的一小部分,则忽略小裂纹扩展阶段并不会影响对整体疲劳寿命预测的准确性.那么小裂纹阶段究竟对疲劳寿命的贡献如何,本文尝试搜集相关文献和数据对此进行论述.
当前的部分研究指出疲劳小裂纹的扩展阶段消耗了整个疲劳断裂寿命的大部分.如文献(Tang et al.2020)中提到的研究(Miller 1987)表明小裂纹扩展阶段占疲劳总寿命的70%~ 80%;吴学仁和刘建中(2006)指出航空铝合金的相关试验结果证明疲劳寿命的绝大部分 (80%~ 90%)消耗在初始长度为10~ 20 μm 的小裂纹向长裂纹的扩展阶段;在文献(Newman et al.1992)中提到20 世纪80 年代的研究表明表面缺陷 (5~ 20 μm) 引起的小裂纹扩展占疲劳总寿命的50%~90%;文献(Gao &Wu 2011)中提到对铝合金疲劳的大量试验研究表明,从初始材料缺陷到长度约1 mm 的小裂纹生长通常占疲劳总寿命的80%以上.
为了澄清小裂纹阶段对疲劳寿命的影响,我们收集了相关研究数据(Miller 1982,Pearson 1975,Ye et al.2017a,Goto et al.2002,Tokaji et al.1988).如图2 所示,Pearson (1975)首次对铝合金的疲劳小裂纹研究结果表明,当疲劳裂纹生长至30~ 90 μm 之间的长度时消耗了整个寿命的45%~85%.通过统计裂纹首次扩展的循环次数,Ye 等 (2017a) 发现GH4169 的小裂纹阶段仅占总寿命的20%~ 30% (图3).当裂纹萌生尺寸被定义为20 μm 的长度时,从图4(a)和图4(b)中可以看出,裂纹萌生寿命分别在疲劳寿命的20%和3%以内,但超过80%的疲劳寿命用于约1 mm 的小裂纹生长.这表明对小裂纹扩展阶段的评估对于疲劳寿命的预测非常重要.
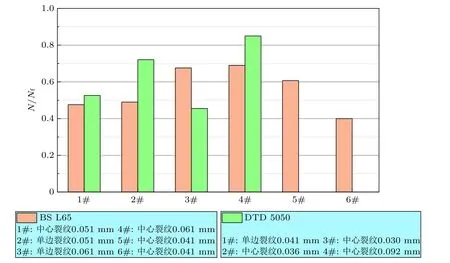
图2 Pearson (1975)的疲劳小裂纹扩展试验结果
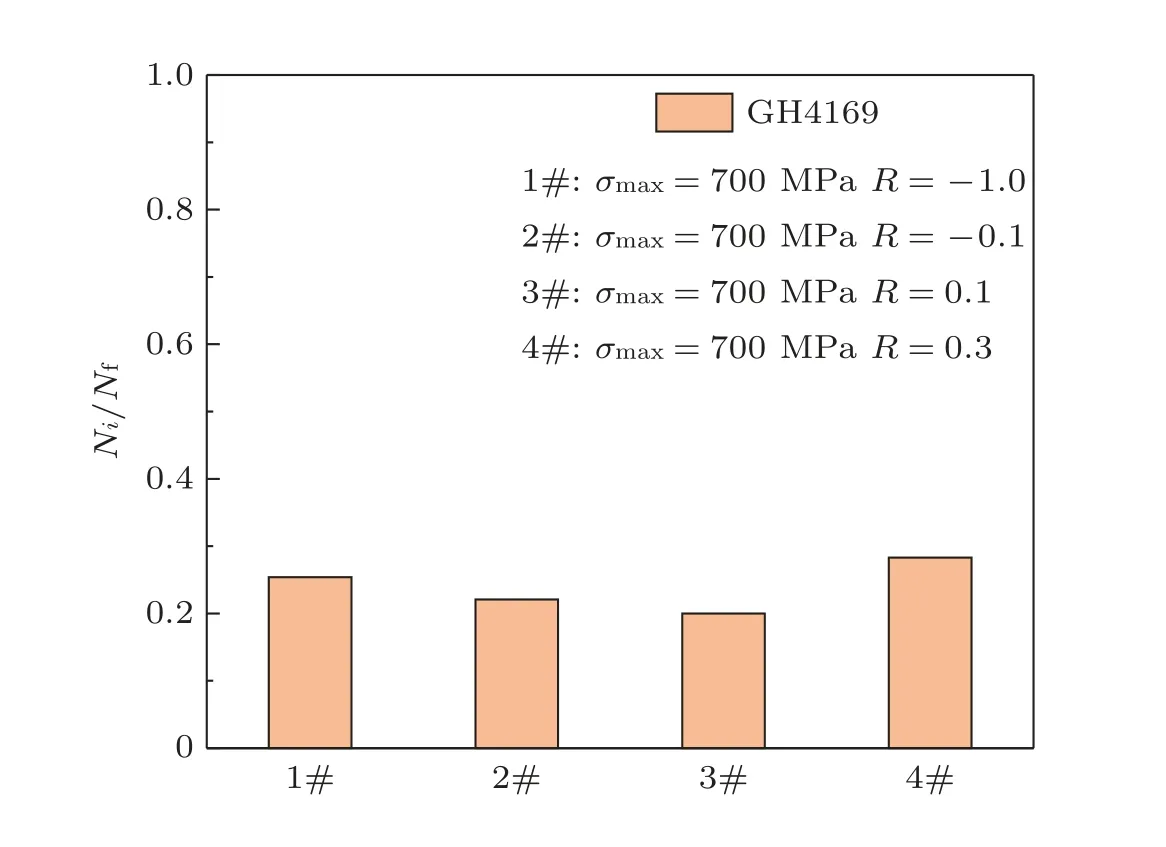
图3 Ye 等(2017a)的疲劳裂纹扩展数据 (其中Ni 是检测到裂纹尺寸首次扩展的循环次数)
图5 显示了疲劳小裂纹和长裂纹生长与寿命的关系.由于当前许多工程部件不包含大的固有缺陷,故失效通常始于表面裂纹,该裂纹尺寸包含在材料单个晶粒内.图5 显示裂纹在表面晶粒中生长时,寿命占比相当大.由此可见晶粒尺寸、缺陷等合金微观特征对裂纹扩展和疲劳寿命有显著影响,这些影响可能占主导地位.而一旦裂纹的长度超过两个晶粒直径尺寸,因其生长速度非常快,故对疲劳寿命的影响很小.

图5 预制裂纹和普通平板试样疲劳期间裂纹的生长(Miller 1982)
首先,上述疲劳小裂纹的相关数据主要出现于上个世纪80 年代左右,是小裂纹效应刚被发现之后一段时间的研究成果,进入21 世纪之后缺乏相关的数据验证;其次,关于小裂纹对整个疲劳寿命的占比结论主要是基于铝合金的研究结果,但具体其他类型的材料如何还需更强有力的数据支撑;最后,疲劳小裂纹尚无明确定义且尺寸划分不尽相同,其对整个疲劳寿命的消耗占比也存在一定的分散性,即从一小部分到绝大部分都有.故可以得出结论,小裂纹阶段对疲劳寿命的消耗要根据实际情况而定,即小裂纹扩展阶段的寿命占比受应力水平、试验环境、应力比以及材料种类等因素的影响.此外,通过对疲劳小裂纹扩展状态的观测表明在相同的驱动力下小裂纹扩展速率较长裂纹快,但有研究指出小裂纹扩展消耗了大部分疲劳寿命,这两点似乎是矛盾的.因此,小裂纹扩展阶段对疲劳总寿命的消耗需要视情况而定.
然而,在HCF 过程中几乎整个疲劳寿命都消耗在小裂纹的形成和扩展阶段(Santus &Taylor 2009).甚至在VHCF 状态下,寿命主要由裂纹萌生和小裂纹扩展决定,这在很大程度上取决于材料的微观结构(Caton et al.2001).另一方面,裂纹在萌生过程中尺寸较小(小于50 μm),尚属于微观小裂纹阶段,且疲劳裂纹萌生阶段占HCF 和VHCF 相当一部分,故微观小裂纹的扩展行为研究就显得很有必要.这是因为研究微观组织小裂纹生长规律可以(1) 得到提高疲劳抗力的微观结构条件;(2) 有助于预测和评估较小载荷条件下的疲劳寿命以及(3) 更好地理解疲劳裂纹产生的位置和原因.但微观小裂纹由于尺寸极其微小难以观测,且不适用于连续介质力学,因此当前的研究还主要集中于形貌观测以及规律探索阶段.另一方面,由上一节可知力学小裂纹和物理小裂纹对整个小裂纹阶段的贡献同样举足轻重,且受力学效应影响,故当前主要是在断裂力学理论框架下对其进行研究,而力学以及物理小裂纹占比究竟如何还不得而知.
疲劳裂纹扩展是一个受微观结构和力学效应影响的过程,这对建立统一的扩展规律模型是不易的.虽然对于力学小裂纹来说,通过修正其驱动力可以得到和长裂纹统一的扩展规律,但这一部分的工作对于裂纹扩展的实时观测和建模来说是具有挑战性的.因为该尺度下的裂纹尺寸较小,且当温度环境较高时 (600 ℃以上) 会严重影响小裂纹行为的观测精度.此外,由于裂纹尖端发生大范围屈服导致线弹性断裂力学理论的失效,故要使用弹塑性断裂力学对小裂纹行为进行分析.而代表弹塑性断裂力学的参量如J积分、COD 以及能量等较难获得,这对疲劳寿命预测模型的建立造成了困扰.因此,力学小裂纹扩展阶段的研究就显得愈发困难.力学小裂纹在整个疲劳裂纹扩展阶段的占比似乎还没有相关文献对此进行过讨论.可以通过对小裂纹扩展阶段的分析,除去微观组织小裂纹消耗的寿命并以此来代表力学小裂纹对疲劳寿命的影响效应,从而得到力学小裂纹的研究价值.如果力学小裂纹阶段对整个疲劳寿命阶段的影响可以忽略不计,则可以适当减少对力学小裂纹研究的投入,为疲劳裂纹扩展提供正确的研究方向.
总之,不论小裂纹在总的疲劳寿命占比如何,有一点已经达成了共识,即所有材料肯定都是有小裂纹阶段的且小裂纹扩展会对疲劳总寿命造成一定程度的消耗.故材料疲劳断裂过程包括裂纹萌生、小裂纹扩展、小裂纹向长裂纹的转变、长裂纹扩展以及最终的断裂阶段.
3 疲劳小裂纹扩展行为
3.1 疲劳小裂纹扩展规律
一般来说,都是针对裂纹扩展速率和扩展路径来表征小裂纹的扩展行为.其中远场载荷、材料微观组织以及加载环境显著影响疲劳小裂纹的扩展行为.
目前,强有力的证据表明在相同的应力比下,小裂纹扩展速率随着最大应力的增加而显著升高.如图6(a)所示,在相同的应力比下,随着最大应力增加到1200 MPa,小裂纹扩展速率增加.此外,还发现小裂纹在扩展过程中是曲折且不连续的.另一方面,在相同的最大应力加载下,应力比也会影响小裂纹的扩展行为.如图6(b)中的FGH96 合金,随着应力比的增加,小裂纹扩展速率逐渐降低.对于Ti-6Al-4V 合金来说,R=-1 时的小裂纹扩展速率整体最高,而R=0.5 状况下的小裂纹扩展速率最低.
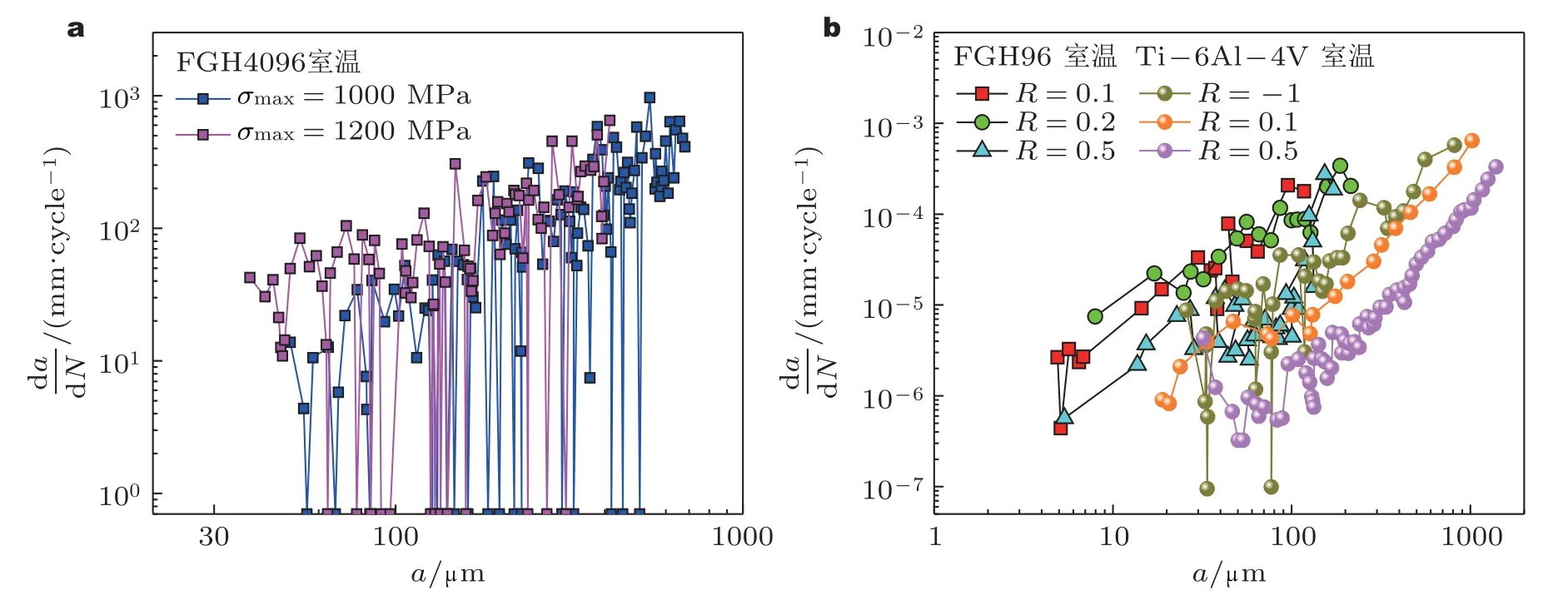
图6 (a)应力比R 为0.1 时,不同峰值应力对合金裂纹扩展速率的影响规律 (缺陷左侧裂纹)(Yang et al.2022),(b)FGH96 合金 (σmax=950 MPa) 和Ti-6Al-4V 合金 (σmax=690 MPa) 在不同应力比下裂纹长度a 和裂纹扩展速率的规律(Liu et al.2023,Caton et al.2012)
疲劳小裂纹的扩展行为首先受材料微观组织 (晶界、孔隙、夹杂等) 的显著影响.其次,外加载荷以及外部环境也会影响小裂纹的扩展行为.在同一载荷和外部环境中,具有平均晶粒尺寸差异的试验结果可以分析晶粒尺寸对疲劳小裂纹萌生和扩展的影响.显然,平均晶粒尺寸较大的试样具有较高的疲劳小裂纹扩展速率 (图7(a)),这表明具有大尺寸晶粒的合金不利于抵抗小裂纹.相反,具有小尺寸晶粒的合金会导致更强的抗疲劳小裂纹特性.因此,随着平均晶粒尺寸增加,小裂纹扩展速率增加.图7(b)中发现小裂纹的扩展速率并不随着裂纹长度的增加而增加,扩展速率发生明显波动,这是因为其扩展行为受微观结构的影响.除了合金固有的微观组织,铸造过程中的缺陷 (如气孔、夹杂等) 也会显著影响小裂纹的扩展速率.如图7(c)中含不同尺寸微孔隙的合金,在相同的应力强度因子范围下具有不同的扩展速率.同时,在所有微孔隙尺寸的试样中都观察到了裂纹停止的现象,尤其是在小裂纹扩展的早期.然而,随着小裂纹的不断向前扩展,具有不同微孔隙尺寸合金的小裂纹速率曲线逐渐接近且变成线性.这表明微组织的影响逐渐减弱,并转变为长裂纹扩展.其裂纹扩展速率开始由Paris 公式描述,不依赖于微孔隙尺寸.

图7 不同材料微观组织对疲劳小裂纹扩展规律的影响.(a) Inconel 617 晶粒尺寸对小裂纹扩展速率的影响(Liang et al.2022),(b) 650 ℃下GH4169 晶粒尺寸对小裂纹扩展速率的影响(Zhu et al.2019),(c) CP-Ti 合金中微孔隙尺寸对疲劳小裂纹扩展速率的影响(Tao et al.2023)
面对燃气涡轮发动机热端部件复杂的工作条件,不仅外加载荷和微观组织会主导疲劳小裂纹的扩展行为,外部环境也会严重影响小裂纹扩展行为.环境因素包括温度以及介质类型,其中腐蚀环境类型对小裂纹扩展行为的影响将在第5 节进行针对性的讨论.如图8,在相同的外加载荷条件下,小裂纹的扩展速率随温度的升高略有增加.这种现象是由于合金的强度变化引起的,例如弹性模量降低,晶界弱化以及滑移系统的激活.发现疲劳小裂纹扩展速率具有明显的温度依赖性,即小裂纹扩展速率随着温度的升高而增加.室温下合金的疲劳小裂纹扩展速率最低,而在980 ℃下测试的试样的疲劳裂纹扩展速率最高.
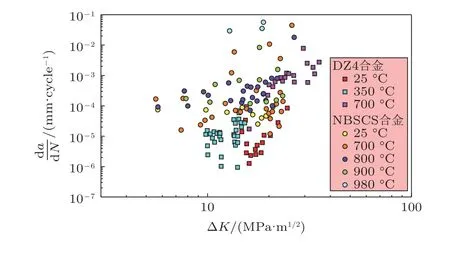
图8 定向凝固合金DZ4 和单晶合金NBSCS 在不同温度下的小裂纹扩展速率(Ma &Shi 2012,Liang et al.2019)
3.2 疲劳小裂纹萌生机制
通常在传统材料的S-N曲线图上可以发现随着外加应力水平的降低,疲劳寿命逐渐趋于无限大,即出现“阶梯”型曲线形状,通常将这一应力状态定义为材料的疲劳极限.在有关HCF、VHCF 的研究(Mughrabi 2002)中强调,疲劳小裂纹的产生过程在更长的疲劳寿命中开始变得重要,并成为决定寿命的关键因素.随着在更低载荷水平下进行疲劳试验,很多研究者开展了寿命远超过107数量级的疲劳试验,有的试验寿命甚至超过1010数量级(Wang et al.2012).结果发现传统的S-N曲线并不能很好的描述VHCF 寿命的分布,在传统的疲劳极限应力水平以下材料仍然可以发生疲劳破坏.即不存在真正意义上的疲劳极限,S-N曲线呈现出“多阶段”形状(Mughrabi 2006).图9 中的S-N曲线显示了两个疲劳极限,大约分别位于106~ 107循环和109~ 1010循环中.

图9 不含夹杂物材料的多阶段型S-N 曲线(Mughrabi 2006)
相关研究表明(洪友士 2022)疲劳极限的变化伴随着疲劳裂纹从材料表面向内部转移的萌生机制变化.疲劳裂纹萌生竞争机制的出现,突破了对传统应力与疲劳寿命关系的认识,即VHCF 寿命的分布呈现出多阶段特征,而传统的S-N曲线无法对此规律进行描述.对于LCF 和HCF,小裂纹往往以驻留滑移带机制起源于材料表面.而VHCF 的主要特点之一是裂纹萌生于材料内部,这是内部萌生竞争胜过表面萌生的结果(Hong et al.2012).VHCF 内部萌生的裂纹在断裂面上呈现“鱼眼”特征,在该范围内往往包含一个表面相对粗糙的独特微观结构形貌,被称为“光学暗区” (ODA) (Murakam et al.1999)、“粗糙颗粒区” (RGA) (Ochi et al.2002)、“粒状亮刻面” (GBF) (Shiozawa et al.2006)或“细颗粒区” (FGA) (Sakai et al.2006).这些名称虽有不同,但都指的是关键缺陷周围的断裂区域,最后裂纹跨过该区域并不断向前扩展直至断裂.图9 所示,对于包含VHCF 的S-N曲线主要呈现出四个阶段: (1) LCF 和HCF 范围,即应力幅值高于局部循环应变阈值,该范围内疲劳寿命是有限的,并遵循Coffin-Manson 定律;(2) HCF 范围内的疲劳极限,应力幅值约在局部循环应变阈值附近.该范围内仍符合Coffin-Manson 定律;(3) 从HCF 极限到VHCF 范围的过渡,载荷幅值低于局部循环应变阈值,在此范围内疲劳寿命很长但有限,这是由于轻微不可逆的随机滑移累积造成材料表面的劣化并引发裂纹(Mughrabi 1999);(4) 对应于VHCF 极限的不可逆阈值,是VHCF 非破坏性滑移和无限疲劳寿命的范围.
对于包含缺陷的材料,疲劳的裂纹萌生位置存在着更加复杂的竞争效应.广泛应用于燃气涡轮发动机材料的镍基高温合金和钛合金由于含有铸造缺陷 (如非金属夹杂、气孔以及疏松),其疲劳失效过程往往伴随着裂纹萌生竞争机制的发生.竞争失效机制在一定程度上会增大疲劳寿命的分散性,增加了寿命预测的难度.显然,疲劳裂纹萌生过程的复杂性在VHCF 状态下最为明显.
在传统的LCF 范围中,大多数情况下疲劳破坏都对材料的表面状态 (如粗糙、夹杂、划伤等) 及其敏感.对于经常在高温环境中工作的镍基高温合金来说,LCF 中的裂纹一般在合金的内部铸造缺陷 (气孔、夹杂) 处萌生.由于HCF 和VHCF 失效往往以裂纹萌生过程为主,而裂纹萌生过程受微观结构特征和缺陷的强烈影响,故疲劳寿命范围通常由受微观组织和缺陷影响的小裂纹生长所决定.在HCF 区 (106~ 107循环) 疲劳裂纹的萌生由表面滑移带、内部孔隙和非金属夹杂物等的竞争决定,但在VHCF 区 (109~ 1010循环) 向内部位置转移.Mughrabi (2002)指出,每个疲劳极限对应于单独的裂纹萌生机制存在于多阶段S-N曲线中,故疲劳机理和裂纹萌生部位的变化导致疲劳寿命的大幅度变化.
由于应力集中效应,合金缺陷位置处有较高的塑性应变,造成疲劳裂纹萌生时间缩短,导致较低的疲劳寿命.夹杂、孔隙等缺陷位置的疲劳裂纹萌生在高强度合金中相当常见.如图10 所示,可以看出存在表面和内部裂纹萌生的竞争失效机制,其中缺陷可能成为疲劳裂纹萌生源.在LCF 和HCF 区域内,疲劳裂纹的萌生是由沿表面滑移带或者缺陷而引发的,即疲劳裂纹既可以由表面夹杂或粗糙引发,也可以由内部非金属夹杂和孔隙等缺陷诱导萌生.然而,在VHCF 区域内,疲劳裂纹总是倾向于内部萌生.在大多数情况下,相对粗糙的独特微观结构形貌从内部缺陷发展并形成,即内部孔隙和非金属夹杂物是诱发内部破坏和VHCF 机制下该区域形成的最有利因素.但是,气孔和夹杂物不是内部失效的必要条件,如图10 所示多相钢和GH4169 合金的VHCF 断口,其内部裂纹并非由内部夹杂诱发.
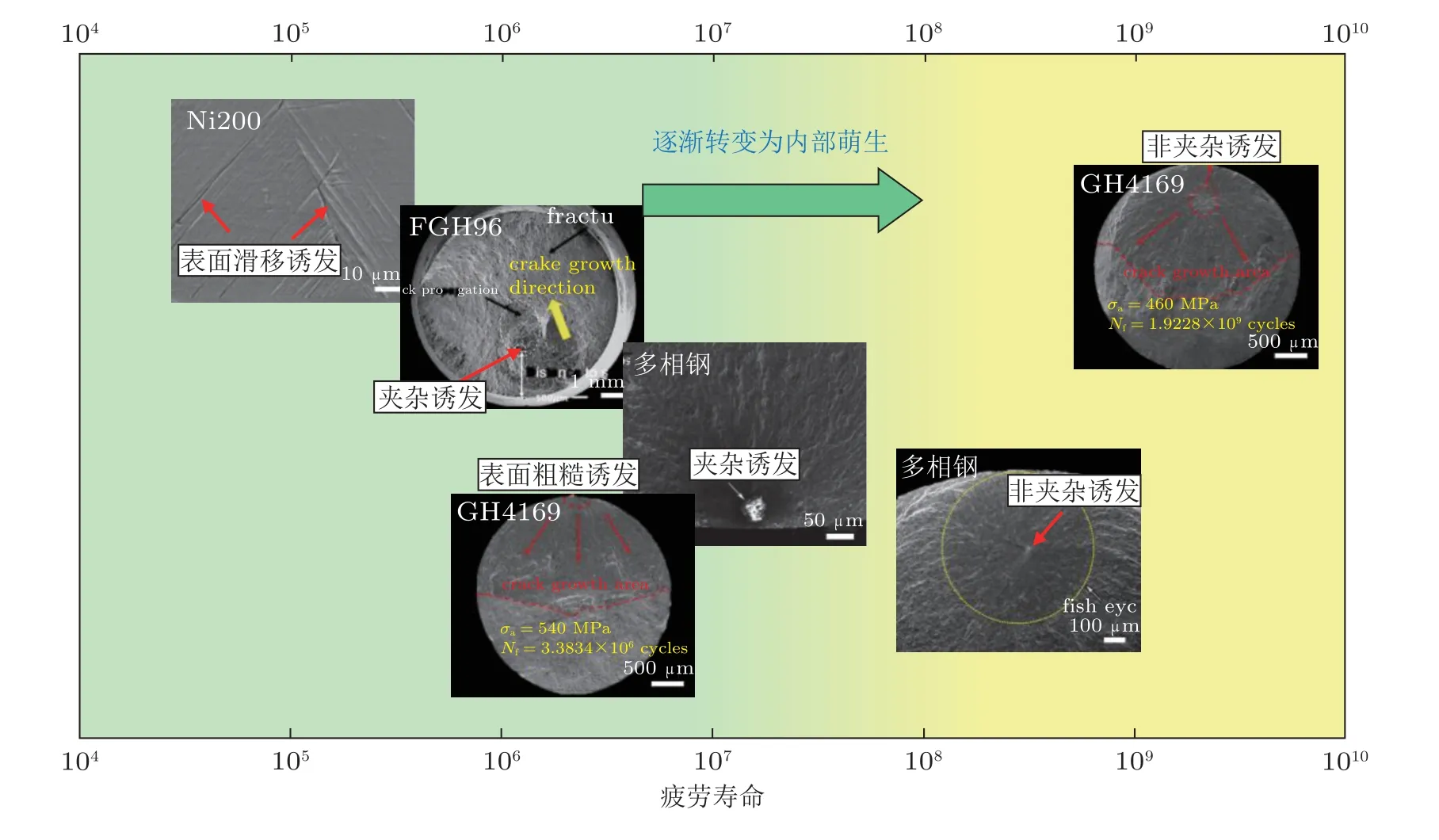
图10 从LCF 到VHCF 区域不同合金的疲劳裂纹萌生机制.Ni200 (Chan et al.2009);FGH96 (Shi et al.2020);贝氏体/马氏体多相钢(Gui et al.2021);GH4169 (Qin et al.2023a)
图11 分别显示了LCF、VHCF 区域中在表面滑移和内部缺陷处裂纹萌生到断裂的过程.在LCF、HCF 区域,小裂纹由表面滑移诱发,随后受到微观组织的影响发生曲折扩展.随着小裂纹生长至合适的尺寸,微观组织的影响减弱并开始受到长裂纹扩展主导,最后直至达到临界尺寸而发生断裂.另一方面,在VHCF 区域,小裂纹由内部缺陷引发并扩展,从而形成粒状亮刻面等典型微观结构区域,该区域属于小裂纹扩展范畴,其扩展受材料的微观组织制约.随着裂纹尺寸的不断增加,逐渐转变为长裂纹扩展最后直至断裂.
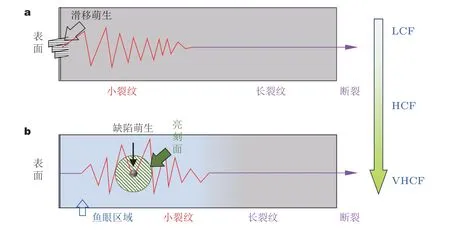
图11 从裂纹萌生到最终断裂的整个疲劳过程示意图.(a)表面滑移引起的裂纹萌生和(b)内部缺陷引起的裂纹萌生
总之,合金的疲劳小裂纹遵循以下萌生机制: (1) 在高应力水平 (LCF) 和中间应力水平(HCF) 下,裂纹萌生于表面滑移或缺陷;(2) 在低应力水平 (VHCF)下,裂纹一般在内部萌生并扩展;(3) VHCF 裂纹的内部萌生不完全是由缺陷主导的.Hyzak 和 Bernstein (1982)报道了两种镍基粉末冶金合金中由孔隙、夹杂物引发的疲劳裂纹,即LCF 范围内的疲劳裂纹有表面引发的趋势;而以裂纹萌生为主的VHCF 范围内疲劳裂纹有内部引发的趋势.总之,疲劳寿命的巨大差异表明从LCF 到VHCF 区域裂纹萌生寿命有显著变化.
3.3 疲劳小裂纹扩展机理
为了揭示造成小裂纹异常行为的潜在机制,近年来相关学者对疲劳小裂纹的扩展行为研究进行了大量的工作.结果发现除了外加应力和外部环境外,小裂纹效应主要是由材料的微观组织主导的,造成其扩展速率和扩展路径具有更高的随机可变性,故疲劳裂纹的扩展过程具有多尺度特征.
首先,应力范围的增加引起裂纹扩展加速,导致疲劳寿命的降低.故峰值载荷和应力比对小裂纹扩展速率的影响可以通过是否引起应力范围的增加而判断.由式(2)可知,当应力比不变时,应力范围随着峰值应力的增加而增加,小裂纹扩展速率显著升高.而在相同的最大应力下,随着应力比的减小,应力范围增加,较低的应力比产生较高的裂纹驱动力,导致小裂纹附近出现更显著的位错运动而产生应力集中效应,有利于疲劳小裂纹的形成和扩展
疲劳加载期间,由于持续的位错运动会形成持久滑移带并产生应力集中,导致疲劳裂纹的萌生.Mbuya 等(2017)证明了疲劳小裂纹扩展行为对合金的局部微观结构非常敏感,也就是说疲劳小裂纹的扩展速率和扩展路径都取决于材料的微观结构属性.通常,晶界被认为是裂纹扩展的主要障碍,即多晶合金小裂纹扩展过程中的波动效应通常归因于晶界的阻挡.当疲劳小裂纹扩展至晶界时,能够观察到小裂纹扩展的阻滞现象,甚至停止扩展(Panwar et al.2018).只有通过增加外应力或进行足够的疲劳循环以产生额外疲劳损伤,裂纹才能继续向前扩展.为了阐明微观结构的影响,Tokaji 等(1986b)对小裂纹的扩展进行了详细的观察,发现当裂纹尖端穿过晶界时,小裂纹扩展速率减小 (图12).但晶界的影响明显依赖于裂纹长度,即影响效应随着裂纹长度的增加明显降低,甚至当裂纹长度超过晶界尺寸的一定倍数时晶界效应消失.
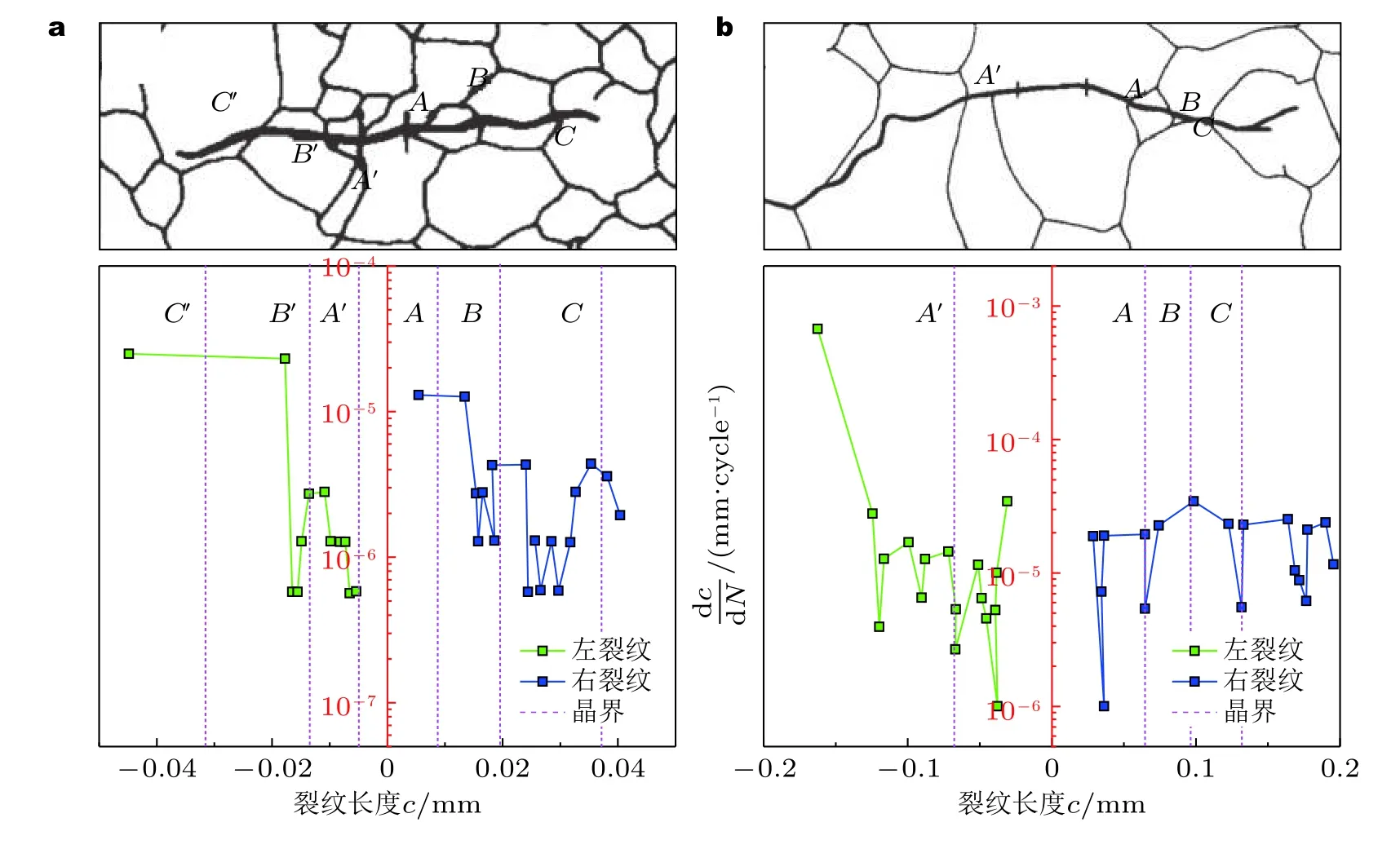
图12 高强度低合金钢SCM435 的奥氏体晶界对疲劳小裂纹扩展的影响(Tokaji et al.1986b).(a)小尺寸晶粒,(b)大尺寸晶粒
近年来,随着先进表征手段的出现和应用,晶界对疲劳小裂纹的影响效应得到了更为深入的理解.开始考虑诸如晶粒尺寸、倾斜、扭转角和裂纹离晶界的距离等特征来量化小裂纹扩展行为,从而揭示微观结构对小裂纹扩展行为的影响.晶粒尺寸的减小会导致晶界的增加,作为小裂纹扩展的微观结构障碍,晶界会多次阻滞小裂纹的扩展,导致更长的疲劳寿命.对于多晶镍基合金Waspaloy,疲劳小裂纹通常沿平面滑移带扩展,裂纹扩展速率有波动(Toh &Rainforth,1996).这与合金的晶粒等微观组织特征有关,晶粒在裂纹扩展的早期阶段都起到了阻碍作用.据报道,Ti-6Al-4V 合金平均晶粒尺寸的减小导致小裂纹扩展速率的减小(Przybyla &McDowell 2012,Lütjering 1998,Tokaji et al.1994).研究表明晶界对微观小裂纹的阻碍是由相邻晶粒的不同晶体取向引起的.当相邻晶粒之间的取向差较小时,裂纹扩展速率并没有减小,这表明相邻晶粒中滑移系统的不利取向是抑制裂纹生长的主要驱动力,而不是晶界本身(Lankford 1982).
Zhai 等(2005,2000)认为扭转角和倾斜角是控制疲劳小裂纹扩展速率和路径的关键因素.Panwar 等(2018)的研究结果表明,在穿越具有较低扭转角和倾斜角的晶界时,裂纹扩展几乎不受影响,而在穿越那些具有较高扭转角的晶界时裂纹扩展速率发生下降.如图13(a),裂纹从滑移面1 穿过晶界扩展到滑移面2.通过α和β两个参数定义了滑移面1 和滑移面2 之间的取向差.参数α是扭转角,即晶界平面上滑移面轨迹之间的角度.β称为倾斜角,它是样品表面滑移面轨迹之间的锐角.这两个参数是控制小裂纹扩展行为的关键参数,代表了裂纹从一个晶粒到另一个晶粒的扩展阻力.由图13(a)显示的abc 区域在晶界平面上必须断裂,裂纹才能穿过晶界,故α越大,来自晶界的阻力就越高.而样品表面上两个有利滑移面的交线之间的角度β,可以通过降低裂纹尖端的驱动力而有助于晶界对裂纹扩展的阻碍.图13(b) 表明,裂纹扩展模式是穿晶和沿晶扩展的组合,但穿晶扩展是主要的失效模式.很明显,对于从晶粒1 穿过晶界进入晶粒2 的小裂纹,它必须克服来自晶界的阻力.由于晶界的强烈阻碍作用,小裂纹通过激活另一种滑移系统改变了其扩展路径,如图13(b4)中裂纹尖端前方区域的滑移线.因此,在晶界处裂纹将选择最小的扭转角和倾斜角,从而使得晶界对小裂纹的阻力最小.当以大的取向差穿过晶界时,小裂纹扩展倾向于被阻止,或造成裂纹扩展路径发生偏转(Hassanipour et al.2019).
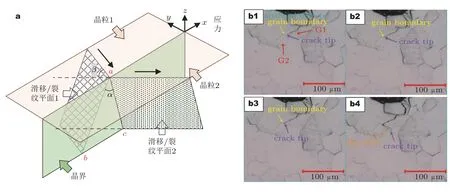
图13 多晶合金的疲劳小裂纹扩展机制.(a)晶界对小裂纹扩展的影响行为,(b1)-(b4)疲劳小裂纹扩展的原位显微图像(Tao et al.2023)
作为燃气涡轮发动机涡轮叶片常用材料,评估单晶镍基高温合金中的疲劳小裂纹生长行为更加具有挑战性,这是因为在小裂纹的扩展过程中不仅失去了晶界的阻挡效应,而且其扩展行为强烈依赖于晶体取向.
借助于显微观察手段,Zhang 等(2019)对镍基单晶高温合金MD2 的小裂纹扩展行为进行了深入的研究.总的来说,小裂纹的产生和扩展与疲劳加载过程中产生的滑移带密切相关.不同的滑移系统可能因不同的晶体取向和测试条件而被激活,从而强烈影响裂纹扩展行为.如图14(a)~图14(d)所示,裂纹都是从最初的滑移痕迹开始的,随着循环加载的继续 (5903 次循环时),这些滑移痕迹中只有一个发展成了裂纹,而其他仍是滑移痕迹.随着裂纹的扩展,在裂纹尖端区域形成了更多的滑移痕迹,裂纹扩展路径开始改变方向.随着加载循环次数的增加,裂纹沿其尖端前形成的滑移迹线扩展,形成锯齿型路径.一些次级裂纹从这些局部滑移痕迹开始萌生,并延缓了主裂纹的生长.总之,主裂纹由靠近其尖端的滑移轨迹所控制,最终形成锯齿型路径.在新裂纹萌生的过程中,主裂纹扩展速率将明显降低甚至发生停止.而在新裂纹合并的过程中,裂纹扩展速率将急剧增加(Zhang et al.2014).

图14 不同取向单晶合金的疲劳小裂纹萌生和扩展过程.(a)-(d)[001],(e)-(f)[111] (Zhang et al.2019);(i)-(k)固定循环数下源于孔隙处的疲劳小裂纹扩展行为(Gall et al.2004)
与[001]取向样品的小裂纹扩展结果相比,最初形成的滑移痕迹较少.然而,在这两种晶粒取向中裂纹都是从产生的滑移痕迹开始萌生的.如图14(e)~ 图14(f),随着加载循环次数的增加,裂纹沿其尖端前形成的滑移痕迹线扩展并形成锯齿型路径.对于[111]取向,锯齿形裂纹特征更明显,故在该取向合金中的断裂表面粗糙度增加.
另一方面,除了合金的晶界特征,其他微观组织,如孔隙、碳化物等对疲劳小裂纹的扩展也有显著影响.在循环载荷的作用下,含有大尺寸孔隙的材料首先在最大孔隙处快速萌生裂纹,随后疲劳裂纹不断生长直至失效.如图14(i)~ 图14(l)所示,裂纹可以在小的孤立孔隙处成核,随后会经历受微观结构特征影响的扩展阶段(Gall et al.2004).在金属间化合物颗粒处小裂纹的生长通常被延缓或被阻止.此外,也经常观察到碳化物处的裂纹分叉和偏转行为.小裂纹扩展早期主要受滑移痕迹的发展控制,当被碳化物阻挡时会发生分叉.此外,由于碳化物的强度和局部应力集中,裂纹可以改变其生长方向或通过颗粒扩展.从图14(g)~ 图14(h)中可以发现小裂纹的生长路径变化.这是由于局部应力集中效应,裂纹被碳化物和微孔所吸引.如果材料的孔隙尺寸大于数百微米,则可以完全绕过微观小裂纹扩展阶段.因此,合金的微观组织 (晶界、孔隙、碳化物等) 特征在决定疲劳小裂纹的扩展路径和扩展速率方面起着重要作用.
由于材料在微观结构上表现出明显的不均匀性或者是随机性,故小裂纹的扩展速率和扩展路径将不可避免地发生波动.小裂纹扩展一方面要依靠循环塑性,而另一方面循环载荷使晶粒内产生的位错塞积阻碍了裂纹的扩展,同时微观缺陷还会影响小裂纹的扩展行为.随着小裂纹的不断扩展,裂纹扩展逐渐受线弹性断裂力学主导但仍受材料微观组织的轻微影响.由于初始时刻裂纹尖端缺乏塑性导致实际驱动力较高,造成小裂纹扩展加速.而随着塑性区域尺寸的增加,裂纹有效驱动力由于闭合效应减小,裂纹扩展速率从而减小(Zerbst et al.2012).当裂纹的尺寸达到特征机械尺寸的量级时 (如裂纹尖端前的塑性区尺寸),将进入力学/物理小裂纹扩展阶段.当裂纹扩展进行到长裂纹阶段时,不再受到材料微观结构行为的影响,并继续扩展直到最终断裂.总之,疲劳裂纹扩展曲线的近门槛值区域 (小裂纹阶段) 偏离了Paris 定律 (出现小裂纹效应).同时,在应力范围门槛值ΔKth以下,这些小裂纹可以轻松地跨越微观结构障碍而发生扩展(Akid &Miller 1991).
3.4 Kitagawa-Takahashi 图
合金的制造缺陷和腐蚀缺陷都会降低燃气涡轮发动机关键部件的抗疲劳性能.因此,定量研究缺陷尺寸对高温合金疲劳强度的影响,对燃气涡轮发动机关键部件的安全寿命设计和缺陷评估具有重要意义.作为简单的抗疲劳工具,经典的Kitagawa-Takahashi 图被广泛地用于描述疲劳极限随缺陷尺寸的变化趋势.
如图15 所示,Kitagawa-Takahashi 图的横坐标为裂纹/缺陷尺寸a,纵坐标为应力水平Δσ.其可以分为两个区域,在缺陷/裂纹尺寸趋向于零的位置,有非扩展裂纹的区域;而在缺陷尺寸大于固有裂纹长度a0的位置,裂纹将扩展并导致疲劳断裂,当外加载荷小于该应力水平时裂纹扩展停止.因此,可以通过收集两个限制参数 (疲劳极限Δσe和疲劳裂纹扩展门槛值ΔKth) 来确定疲劳裂纹扩展的下限(Sadananda et al.2019).水平线AB 为表面光滑试样的疲劳极限范围Δσe,图中的斜线BC 代表了长裂纹应力强度因子范围ΔKth.El-Haddad 模型以Kitagawa-Takahashi模型为基础,考虑了小裂纹效应,在实际缺陷尺寸的基础上增加了一个固有裂纹长度.对于小裂纹效应占主导的数据,El-Haddad 模型相对来说更加接近.可以通过大量的试验来确定含缺陷或裂纹材料的疲劳极限.如果疲劳极限和长疲劳裂纹扩展门槛值具有合理的精度,也可以通过El Haddad 关系进行估算.对于给定的外加载荷和给定的缺陷或裂纹尺寸,它可用于确定裂纹止裂.
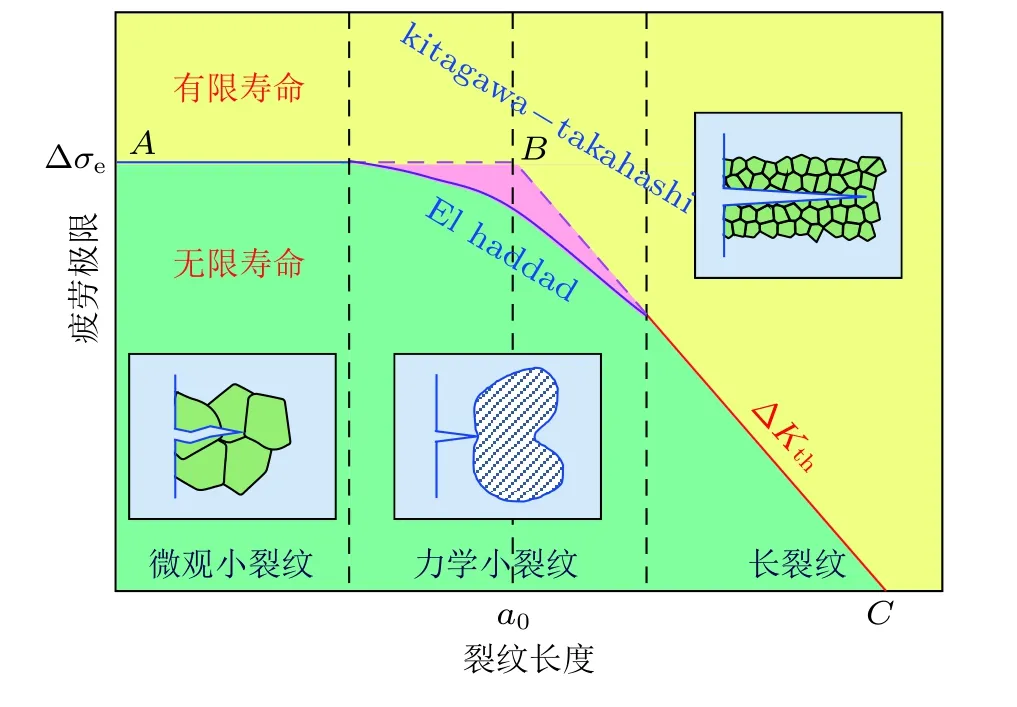
图15 区分了微观结构小裂纹、物理小裂纹和长裂纹三个区域的Kitagawa-Takahashi 示意图
由于Kitagawa-Takahashi 图能够将缺陷/裂纹和合金的疲劳行为联系起来,因此其也适用于含有腐蚀坑的腐蚀疲劳裂纹扩展行为.Chan 等(2013)基于ME3 合金的低温热腐蚀 (含有腐蚀坑) 疲劳数据,将腐蚀坑生长到裂纹扩展的转变过程用Kitagawa-Takahashi 图进行了关联.如图16(a)和图16(b)所示,分别显示了ME3 合金纯疲劳和腐蚀疲劳的Kitagawa-Takahashi 图.
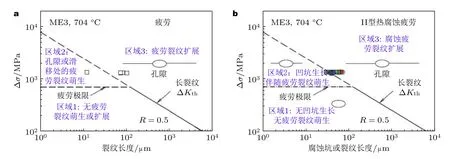
图16 Kitagawa-Takahashi 图中纯疲劳和热腐蚀疲劳的损伤机制比较.(a)纯疲劳和(b)热腐蚀疲劳(Chan et al.2013)
在没有腐蚀环境的情况下,ME3 合金的疲劳裂纹萌生发生在孔隙或滑移带处(Gabb et al.2010).当裂纹尺寸超过疲劳长裂纹扩展门槛值时,疲劳裂纹不断向前扩展到失效.图16(a)描述了代表三种不同疲劳损伤机制的三个区域: 区域1 位于疲劳极限以下,无疲劳裂纹萌生和扩展发生;区域2 位于疲劳极限以上的应力范围内,以滑移带或孔隙处的疲劳裂纹萌生为主,当裂纹尺寸超过虚线时生长至长裂纹;区域3 位于大于长裂纹门槛值 (实线或虚线) 的裂纹尺寸处,主要是在临界裂纹长度下长裂纹向断裂的扩展.另一方面,通过绘制应力范围作为腐蚀坑/裂纹尺寸的函数来表示腐蚀疲劳的Kitagawa-Takahashi 图.小裂纹始于腐蚀坑,并在热腐蚀环境的影响下扩展.作为比较,图16(b)描述了代表三种不同腐蚀疲劳损伤机制的三个区域: 区域1 位于疲劳极限和长裂纹门槛值之间,以无腐蚀坑生长为主;区域2 位于疲劳极限以上的应力范围内,也以腐蚀坑生长为主,且腐蚀坑处伴有疲劳裂纹萌生,当腐蚀坑或裂纹尺寸超过虚线时生长至长裂纹;区域3 位于大于长裂纹门槛值 (实线或虚线) 的腐蚀坑/裂纹尺寸处,主要是在临界裂纹长度下长裂纹向断裂的扩展.图16(b)中的数据为热腐蚀环境中ME3 合金的临界坑尺寸试验数据(Gabb et al.2010).所有临界腐蚀坑都聚集在长裂纹门槛值线上或右侧,这表明临界腐蚀坑尺寸受疲劳长裂纹扩展门槛值的控制.
此外,在Kitagawa-Takahashi 图中,由于长裂纹应力强度因子门槛值和疲劳极限相关,故该图能够预测含腐蚀坑部件的耐久应力,其中ΔK是使用半表面宽度c的值计算的.通过将固有裂纹长度c0加到实际长度c上,将El Haddad 等(1979)的表达式包括在小裂纹阶段中.Schönbauer等(2014)将腐蚀疲劳数据绘制在修正的Kitagawa-Takahashi 图中 (图17),横坐标为标准化裂纹尺寸c/c0,纵坐标为标准化应力强度因子范围ΔK/ΔKth,其中腐蚀坑的疲劳破坏门槛值和固有裂纹长度c0由下式给出式中,Y是几何因子,σe为疲劳极限.等式(3)用于评估小裂纹的应力强度因子门槛值,裂纹从凹坑位置处萌生并扩展而失效.如图17 所示,针对空气和腐蚀环境中测试条件构建的修正Kitagawa-Takahashi 图,得到小裂纹应力强度因子门槛值的估计,如图中的虚线所示,与试验数据相比获得了良好的估计.
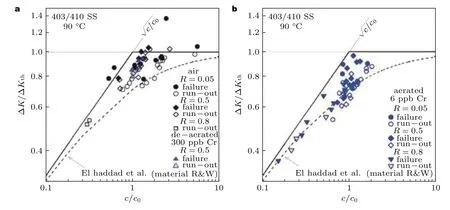
图17 预制坑试样疲劳试验的修正Kitagawa-Takahashi 图.(a)空气和300 × 10-6 Cl-溶液,(b) 6 × 10-6 Cl-溶液(Schönbauer et al.2014)
4 疲劳小裂纹扩展模型
燃气涡轮发动机热端部件的损伤演化是一个多尺度过程,在宏观尺度上表现为结构性能的下降,在微观尺度上表现为微裂纹的萌生与扩展.因此,正确捕捉小裂纹的扩展规律并建立小裂纹扩展模型是获得结构件精确寿命的关键.针对小裂纹问题,北京航空材料研究院与NASA 兰利研究中心曾针对高强度航空铝合金7075 和LC9cs 进行了合作研究,通过将ΔK与裂纹闭合概念相结合,提出了一种适用于小裂纹扩展分析的全寿命预测方法(Newman et al.2000).该项目的目标是研究小裂纹扩展的规律,在经典的S-N曲线和损伤容限方法之间建立联系,并利用断裂力学方法提高裂纹扩展和疲劳寿命预测能力,最终提高结构件的可靠性和安全性.这一方法已被不断改进并成功地推广应用到多种航空材料.
在该合作研究的模型中,首先采用三维有限元法和权函数法确定了表面裂纹和缺口处角裂纹的应力强度因子.随后,通过考虑塑性诱导的裂纹闭合效应并针对各种裂纹形态参数建立了有效应力强度因子方程,用于小裂纹数据的关联和寿命预测.该模型能够考虑小裂纹扩展中的闭合效应,故能够准确预测小裂纹的加速效应.但小裂纹扩展的驱动力还是基于线弹性断裂力学参量K,且没有考虑材料的微观组织对小裂纹扩展行为的影响,故无法捕捉小裂纹的波动效应.由于该模型无法将材料的微观组织与小裂纹的扩展行为联系起来,因而无法预测小裂纹扩展过程中的波动甚至停滞现象.
4.1 超高周疲劳寿命预测模型
对于HCF、VHCF 来说,总寿命的大部分被裂纹形成阶段所消耗.可以使用考虑裂纹萌生因素的模型估算HCF 和VHCF 寿命.由于裂纹的萌生存在表面和内部竞争机制,因此在寿命预测模型中必须考虑其萌生机制才能更加精确的描述S-N曲线的多阶段特征.当前,我们收集了三种针对VHCF 的研究模型,主要有: (1) Murakami 等提出的疲劳极限预测方法及其修正模型;(2) 基于疲劳指示参数 (FIP) 来预测疲劳寿命的方法以及(3) 半确定性的VHCF 裂纹萌生模型.
低疲劳强度归因于初始缺陷,这些缺陷往往在合金制造过程中形成,并从疲劳试验结果和断裂表面中暴露出来.Murakami 等(2002)首先提出参数来预测疲劳极限参数来预测疲劳极限,即通过考虑VHCF 典型区域 (FGA 等微观结构区域) 周围的面积,基于Murakami 模型预测的疲劳极限σw为
式中,A为常数系数,其值取决于缺陷的位置,R为应力比,α是一个常数系数.
Qian 等(2020)提出了一个新的材料常数Am,考虑到内部或表面裂纹萌生系数和材料硬度都是常数.此外,考虑到试样的几何形状对裂纹萌生的影响,引入了断裂面半径r并使用了distance 与r的比值.因此,提出了一个修正的Murakami 模型,以包括裂纹萌生效应
式中,Am、β1、β2、β3是可以使用最小二乘法通过线性回归确定的常数;r和distance 的值在图18中显示.提出的模型很好地预测了内部和表面裂纹萌生的疲劳强度.

图18 考虑裂纹萌生位置的疲劳强度预测结果(Qian et al.2020)
还有一种方法即使用疲劳指示参数FIP 来预测LCF、HCF 和VHCF 寿命,FIP 认为是疲劳裂纹萌生和扩展的驱动力.为了捕捉裂纹萌生尺寸的相关性,Cervellon 等(2017)基于CMSX-4采用了FIP 来预测疲劳寿命
式中,μ为Schmid 因子,Δσ为施加的应力范围,E杨氏模量,参数k等于1,以获得相似的机械和塑性贡献.ΔKth是应力强度因子门槛值范围,σ是施加的正应力,Adefect为用环绕圆法在断口上测得的孔隙面积,对于内部萌生Y等于0.5,而对于表面萌生为0.65.基于多晶镍基高温合金K418,Li 等(2021)在考虑了裂纹的萌生位置的基础之上提出了相应的FIP 疲劳寿命预测方法.对于HCF 和VHCF,变形主要由弹性应变控制,因此Coffin-Manson 方程的塑性阶段可以忽略.将FIP 带入Coffin-Manson 方程可得FIP 和循环数Ni之间的关系为
式中,b为材料常数,FIP 值可由式(6)得到.基于单晶CMSX-4 和多晶K418 合金,采用FIP 寿命预测结果在图19 中显示,表明该方法针对HCF 和VHCF 区域的寿命预测结果良好.
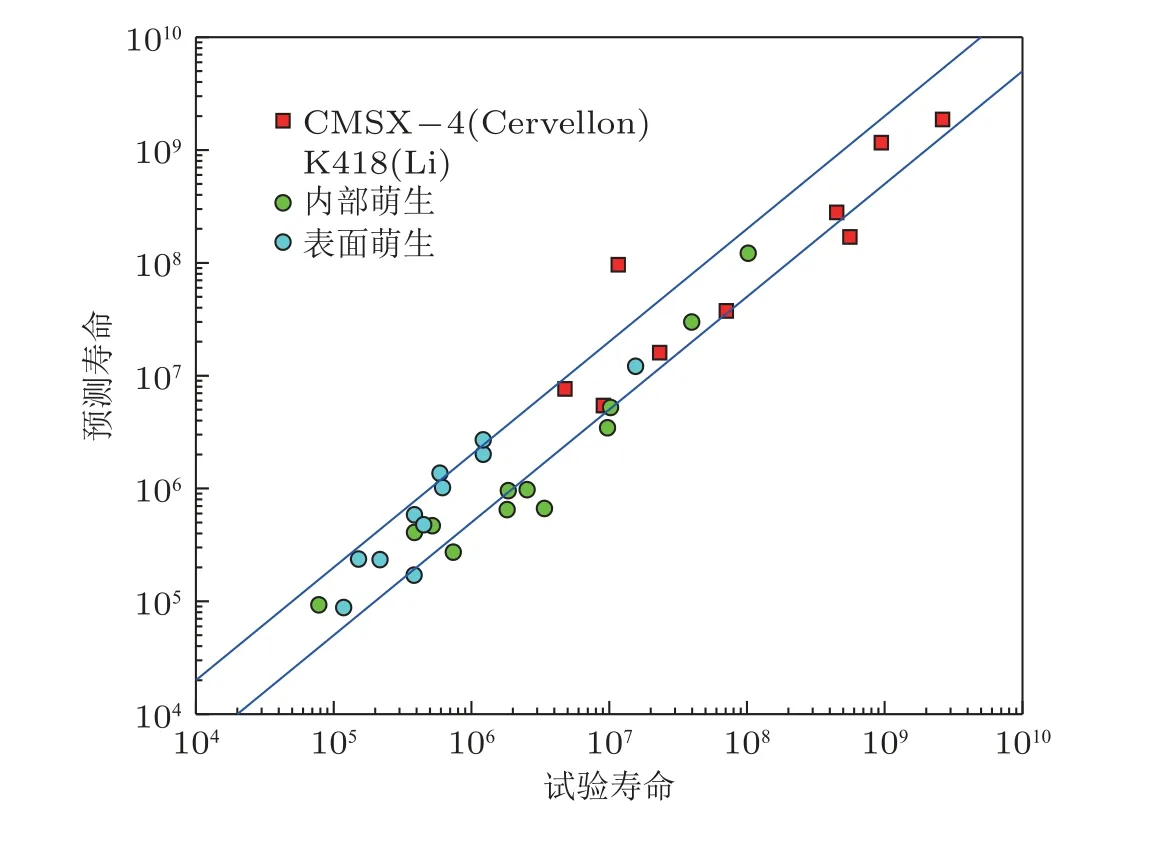
图19 使用FIP 方法预测的HCF 和VHCF 寿命与实际寿命的比较
另一方面,Mughrabi (2006)还提出了一个半确定性模型,可在低于持久滑移带 (PSB)阈值的载荷水平下 (图9 中的第3 阶段) 预测VHCF 裂纹的萌生寿命
式中,n是循环硬化指数,σs,th为饱和应力,σs,th=σPSB,σs,i是PSB 阈值应力以下的应力范围,pth/pi为滑动不可逆性的比率.模型假设在HCF 疲劳极限 (第2 阶段) 结束时,饱和应力值σs,th刚好低于PSB 阈值,在足够的应力集中下获得临界粗糙值以致在Nth个循环后引发疲劳裂纹.如果忽略滑移不可逆性对载荷幅值的依赖,可以得到相应的近似解
在较低的应力σs,i下将导致表面粗糙达到临界值,应力集中效应将增大局部应力水平,因此疲劳裂纹将在较低应力下萌生.随后,使用铜对两种近似进行定量评估,形成了具有疲劳裂纹萌生寿命的S-N曲线图 (图20) .在所考虑的非常低的振幅下,预计初始阶段将占据疲劳寿命的主要部分,因此Ni≈Nf.最后得出结论,根据Nth的实际值,应该可以在VHCF 试验中检测第3 阶段内的疲劳寿命曲线的预测过程.
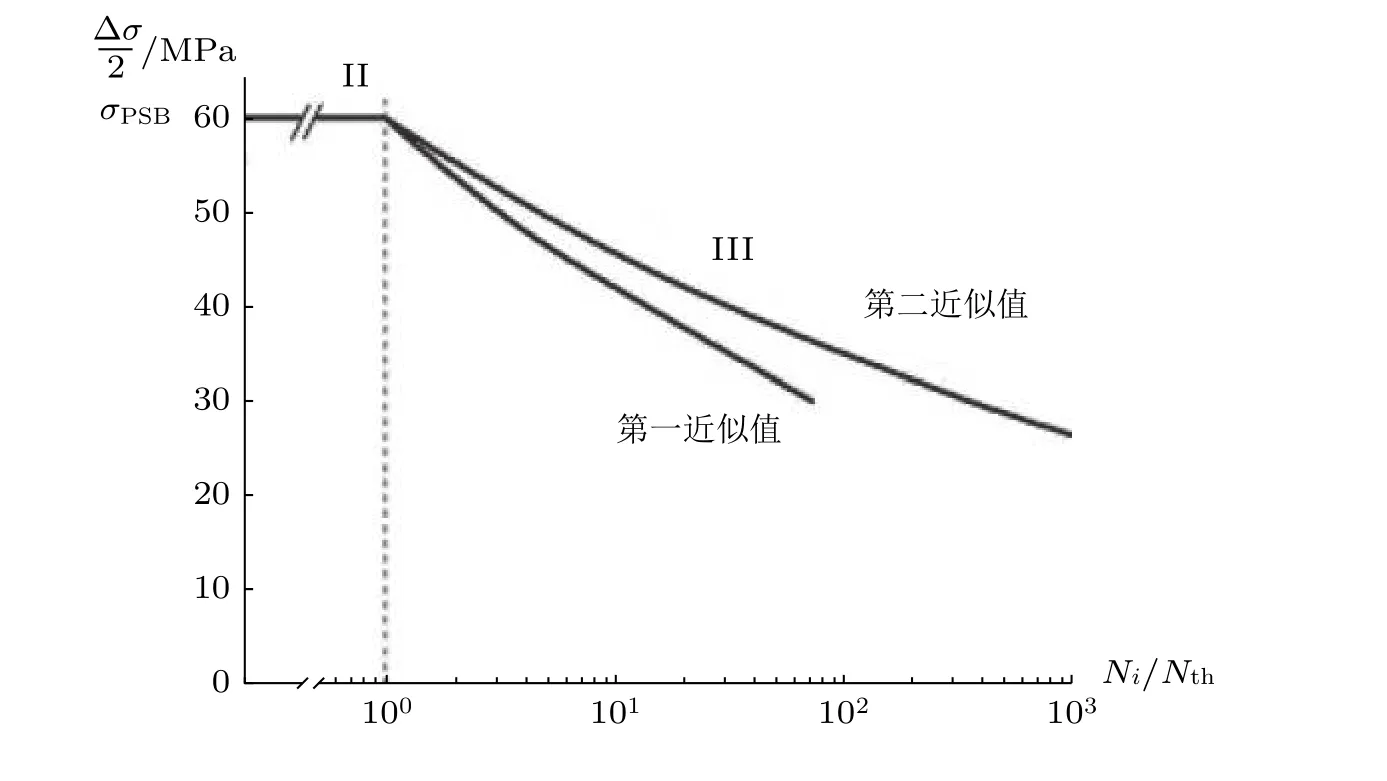
图20 VHCF 第3 阶段下疲劳裂纹萌生寿命的预测结果,根据方程(9)计算
由于裂纹的萌生存在复杂的竞争机制,当前的疲劳模型只考虑了缺陷的尺寸、位置,且都是基于单一机制下的预测,缺乏对缺陷竞争效应更为细致的描述.另一方面,在大多数情况下,内部孔隙和非金属夹杂物萌生是诱发内部破坏和VHCF 机制下FGA 形成的最有利因素,但气孔和夹杂物并不是内部失效的必要条件.根据试验观察,FGA 形成似乎是VHCF 区疲劳破坏的必要条件.因此,裂纹萌生和微观结构之间的相互作用对于完全理解FGA 形成和VHCF 破坏的潜在机制是一个关键问题.
4.2 基于材料微观组织结构小裂纹扩展模型
Hobson (1982)提出了一个尚未穿过第一个晶界的小裂纹扩展模型,用于描述第一晶粒内表面小裂纹扩展的方程为
式中,C和α为材料常数,d为晶粒尺寸.该方程假设小裂纹将在晶界处停止扩展,即当a=d时,da/dN=0.虽然该模型体现了剩余滑移带塑性区(d-a)和裂纹长度a,但无法考虑应力水平以及相关的小裂纹扩展机制,故并没有得到广泛的应用.之后,Brown-Hobson 模型(Miller 1989)通过引入应力描述疲劳小裂纹扩展状态,其方程表示为
式中,A和α是材料常数,Δγ表示所施加的剪切应变范围.在原始的Brown-Hobson 模型中,对于方程(11),分别使用应力范围Δσ和应变范围Δε.
早期的这些模型虽然可以描述小裂纹的扩展规律,但都是在假设小裂纹在达到第一个晶界时发生停止的基础之上的,故其仅仅局限于第一个晶粒内,并无法揭示晶界对小裂纹的阻滞效应.因此,Luster 和Morris (1995)使用几何相容性因子m'的值研究了穿过晶界的滑移转移,该因子定义为
式中,κ为相邻两个晶粒之间的滑移矢量角度,φ是垂直于这些晶粒的滑移面之间的角度,m'的值越低代表滑移转移越困难.该几何相容性因子虽然能够快速研究晶界对小裂纹的阻滞效应,但却无法考虑到晶粒取向对晶界强度的影响.随后,Wilkinson (2001)的模型纳入了相邻晶粒取向和扭转角的影响,使用滑移面1 的Sachs 因子(mcurrent)与滑移面2 的Sachs 因子(mnext)之比来考虑相邻晶粒的取向效应.临界应力S(r0)即裂纹穿过晶界所需的应力,为了防止应力奇异性,将其确定在相邻晶粒中离晶界的距离r0处,其表达式为
式中,α0是校准参数,而Sct是在裂纹路径方向不变的情况下,裂纹穿过晶界传播所需的临界应力.在此基础之上,Panwar 等(2018)考虑了倾斜和扭转角、取向差、Schmid 因子和临界裂纹扩展应力之间的耦合,并综合上述模型提出了一种新的裂纹-晶界相互作用模型来描述裂纹的延迟/止裂.假设当前晶粒和下一个晶粒的Schmid 因子之比、倾斜和扭转取向差以及临界裂纹扩展应力直接影响小裂纹扩展速率.因此,临界应力S(r0)由下式给出
式中,M是Schmid 因子,由于扭转角对小裂纹的扩展有更大的影响,导致函数的形式较为复杂,故用指数分布来表示.这三个函数关系如下所示
式中,kl是来自拉伸屈服强度的Hall-Petch 关系的参数,r0用于防止应力奇异,通常使用0.1 到1 μm 之间的值.图21 为基于该模型的预测结果,实心点表示裂纹在晶界处被阻止,而空心点表示裂纹扩展被延缓或不受晶界的影响.用红色显示的点表示模型预测和试验之间的不匹配.可以发现在低扭转角和倾斜角的情况下裂纹扩展不受晶界影响.
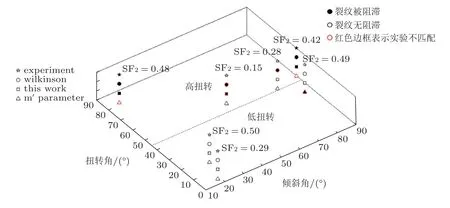
图21 含晶界特征的疲劳小裂纹模型 (不同扭转角和倾斜角) 预测结果对比(Panwar et al.2018)
4.3 基于修正的线弹性断裂力学小裂纹扩展模型
裂纹扩展速率的量化涉及两个方面: 第一个方面是明确定义和量化裂纹尖端驱动力,第二个方面是材料对裂纹扩展的阻力.因此,在确定裂纹尖端驱动力时,不仅需要考虑外部施加应力所产生的力,还需考虑内部应力所引起的力.
解决这一问题的一个关键方法是探索裂纹尖端驱动力的物理合理表达式.为了更好地描述小裂纹扩展行为,大多数研究人员试图通过修改应力强度因子范围将疲劳长裂纹扩展速率模型外推到小裂纹区域(Newman et al.1994,Chan &Lankford 1988,Vallellano et al.2009,Ye et al.2018,Tang et al.2020,Chapetti 2003,Wang et al.2014,Bang &Ince 2020,Maierhofer et al.2014).这些模型在物理参数的定义和理论基础上各不相同.一般来说,它们是基于Paris 定律的经验类型.为了描述小裂纹扩展的行为,先前的修正模型(Chowdhury &Sehitoglu 2016)基本上可以采用以下表达式
式中,a为半表面裂纹长度,N为疲劳循环数,参数C和m由长裂纹生长速率的拟合数据给出,ΔKeff为有效应力强度因子范围,即ΔKeff=Kmax-Kmin.由于疲劳裂纹不能在传统意义上的门槛值Kth以下扩展,故将Kmin替换为应力强度因子门槛值Kth.也就是说,ΔKeff应解释为有效应力强度因子范围,即ΔKeff=Kmax-Kth.由此得到以下裂纹扩展模型(Xiulin &Hirt 1983)
式中,σf和εf分别为材料断裂强度和断裂延性,其中
式中,R是应力比,ΔKth0是R为0 时的门槛值,γ是材料常数.虽然该模型具有良好的预测物理小裂纹扩展速率的能力,但在微观组织小裂纹阶段具有局限性.同时,模型中引入了如应力比R、材料断裂强度σf和断裂延性εf等物理参数,削弱了Paris 定律的经验性能.
Newman 等(1981,2000)及Zhao 等(1989)认为应力强度因子范围不足以代表裂纹尖端驱动力,故他们尝试从裂纹闭合效应的角度来解决这一问题.假设直到循环载荷足够大,使得裂纹可以完全张开,裂纹才会扩展.因此,有效应力强度因子范围ΔKeff的概念被引入并定义如下
式中,ΔKop是张开应力强度因子范围.它与应力有关,能使裂纹尖端完全打开.尽管该模型也是幂函数形式,但与先前模型的显著区别在于,门槛值ΔKth被张开应力强度因子范围ΔKop替代.通过引入裂纹闭合效应,Newman 将裂纹闭合视为裂纹长度的函数,这表明随着裂纹长度的增加,裂纹闭合效应将更加明显.
4.4 基于弹塑性断裂力学小裂纹扩展模型
寻找合适的裂纹尖端驱动力对于小裂纹扩展行为的预测是非常重要的.虽然之前的研究基于ΔK进行了一系列的修正工作,但这都是以线弹性断裂力学为基础的,由于线弹性断裂力学不再被认为能够关联小裂纹扩展速率,因此必须使用弹塑性裂纹驱动力参量来代替,如裂纹尖端塑性、J积分范围ΔJ、裂纹尖端张开位移范围ΔCTOD 和应变能强度因子范围ΔS.图22 表明合适的弹塑性驱动力能够较好地描述小裂纹扩展规律.例如,在小裂纹扩展阶段,裂纹尖端会出现大范围屈服,故循环塑性变形是疲劳小裂纹扩展的主要机械驱动力.塑性区大小rp等参数已经被证明是表征疲劳小裂纹扩展行为的合适参数(Ye et al.2017b).如图22(b)所示,不同温度下的裂纹扩展速率和塑性区大小rp呈现明显的线性关系.
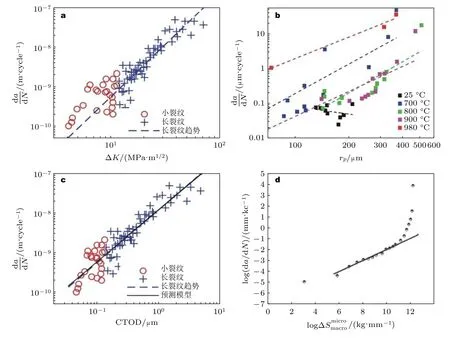
图22 不同裂纹扩展参量和小裂纹扩展速率之间的关系对比.(a) GH4169 合金的驱动力参数应力强度因子K 与裂纹扩展速率,(b)不同温度下的镍基单晶合金NBSCS 的驱动力参数塑性区尺寸rp 和小裂纹扩展速率,(c) GH4169 合金的驱动力参数裂纹张开位移CTOD 与裂纹扩展速率,(d) 2024-T3 铝合金的驱动力参数应变能强度因子范围ΔS 和小裂纹扩展速率(强度因子范围ΔS 和小裂纹扩展速率(Zhang et al.2022,Liang et al.2019,Sih &Tang 2014)
已经提出了许多基于不同塑性参数的模型,包括不可逆位错和塑性累积.Shyam 等(2005)提出了基于位错的模型
式中,κ是一个经验常数,与材料特性、温度和加载频率相关.刃位错(φc)分布引起的循环裂纹尖端位移由以下表达式给出
对于刃型位错,单调裂纹尖端位移(φm)为以下表达式
式中,ν为泊松比,E为杨氏模量,σys为单轴I 型加载的材料屈服强度,载荷比效应来自φc.通过Shyam 模型可以准确预测小裂纹扩展行为,但无法合理解释微观小裂纹的波动,并且裂纹扩展速率被认为与循环CTOD 的乘积线性相关,这可能在一定程度上导致该模型的应用受到限制.鉴于Shyam 模型在承受的应力大于材料屈服极限时无法使用,Deng 等(2015)将完全屈服理论引入φm和φc的修正中,并利用幂函数类型来拟合试验数据.然而,该模型仅反映了小裂纹阶段裂纹扩展的一般趋势而未考虑小裂纹扩展速率的波动效应.总之,基于裂纹尖端塑性模型的这种局限性仍然难以克服.
Polak 和Harkegard (2005)的试验结果指出相对于线弹性参量K,采用弹塑性断裂力学参量J积分范围,裂纹扩展速率曲线表现出更强的相关性,且可通过幂律相关性进行近似。故他们通过引入裂纹扩展速率定律ΔJ0的参数,对Dowling 和Begley 模型进行修正,模型如下
式中,v0=10-6m·cycle-1,参数γ和ΔJ0使用最小二乘法确定.模型的拟合结果表明,该模型能够描述MSC 的机制.然而,由于该模型中忽略了裂纹闭合效应,预测的疲劳寿命结果可能导致偏危险.疲劳寿命的计算是通过对Paris 定律裂纹扩展速率方程进行积分来完成的,Döring 等(2006)试图通过引入有效的J 积分给出了相应的疲劳裂纹扩展速率
这个模型的材料参数是用长裂纹扩展数据确定的.假设J积分和应变能密度贡献之间成比例,其中Y是应力强度因子的几何函数
式中,(虚拟) 应变能密度仅针对张开裂纹范围进行计算,有效J积分范围ΔJeff与使裂纹完全张开的有效应力σeff相关.值得注意的是,弹塑性变形、裂纹闭合效应、循环软化和硬化都包含在该模型中.
Zhang 等(2022)将CTOD 作为驱动力提出了相应的模型来计算小裂纹的扩展速率,即裂纹尖端张开位移是小裂纹扩展的驱动力参数.最后,小裂纹扩展阶段的CTOD 可以写成
式中,a为裂纹长度,σop,s和分别为小裂纹张开应力和局部屈服强度,表达式为
式中,σfl是疲劳极限,γ是微结构差异系数,控制从小裂纹扩展到长裂纹扩展阶段的转变速度,D是平均晶粒尺寸.从而小裂纹的扩展速率为
式中,C1,m1是拟合系数.考虑裂纹闭合演化和微观结构差异,对CTOD 进行了修正.图22(c)表明基于GH4169 合金,所提出的模型预测结果与试验数据一致.
应变能密度是指存储在裂纹尖端前方体积单元中的应变能,它是应力的二次形式.应变能存储在微观或宏观尺度上.故应变能密度因子S可被视为失稳起始时的释放能量,并在疲劳评估中用作裂纹扩展参量.应变能密度因子在不同尺度上的灵活性使其成为多尺度问题的良好候选.Sih 和Tang(2014)建立了多尺度疲劳裂纹扩展模型.尺度范围分为微纳米、纳米微、微宏观和宏观.随后他们将ΔS视为裂纹尖端驱动力以开发多尺度模型.载荷、材料和几何形状的影响都包含在模型中,其表达式如下
图22 对比总结了基于线弹性断裂力学小裂纹扩展参量和弹塑性断裂力学小裂纹扩展参量的对比结果.可以发现,无论是否考虑塑性,裂纹扩展参量都可以准确描述长裂纹的扩展行为.但相对于线弹性参量K,其它弹塑性断裂力学裂纹扩展参量明显能够更好的描述小裂纹的扩展趋势,其关系在对数坐标下呈现较好的线性关系.故基于弹塑性断裂力学建立的小裂纹扩展参量是最适合于描述小裂纹扩展行为的.
5 腐蚀环境中的疲劳小裂纹扩展行为
5.1 燃气涡轮发动机的环境损伤
由于现代高性能燃气涡轮发动机愈发恶劣和复杂的服役环境,其涡轮盘、叶片等关键部件因环境因素 (氧化、冲蚀及热腐蚀等) 的影响,从而呈现出复合疲劳破坏的多模式损伤.腐蚀环境将改变热端部件的表面形貌,使其更易于发生裂纹萌生并加速裂纹的扩展,降低部件的使用寿命,甚至导致灾难性事故的发生,成为影响燃气涡轮发动机安全运行的隐患之一.因此,为保障燃气涡轮发动机安全运行,亟需预测材料在腐蚀环境中的疲劳寿命以避免重大的事故发生和巨大的经济损失.
热腐蚀疲劳损伤演化过程可分为5 个阶段: 腐蚀缺陷生长阶段、热腐蚀缺陷-小裂纹转换阶段、小裂纹扩展阶段、长裂纹扩展阶段和断裂阶段.但是,对于热端部件材料来说,小裂纹扩展阶段至关重要.不仅因为小裂纹会影响疲劳寿命,更重要的是小裂纹阶段关联环境驱动的热腐蚀缺陷生长与力学驱动的裂纹扩展.另外,对于燃气涡轮发动机涡轮叶片等关键部件来说,一旦检测出宏观裂纹就意味着服役寿命的结束.因此,如何准确量化小裂纹扩展行为是正确预测疲劳寿命的前提.但是,在一定的小裂纹尺寸范围内,由于材料微观结构等因素影响,小裂纹的扩展速率要远远高于长裂纹.基于传统的长裂纹扩展模型进行寿命预测,将使得热端部件的实际寿命往往低于理论预估值.故深入研究材料在腐蚀和机械载荷耦合条件下的小裂纹扩展机理和模型,建立能够应用于燃气涡轮发动机热端部件的腐蚀疲劳寿命预测方法具有重要的理论意义和广阔的应用前景.
5.2 腐蚀疲劳小裂纹扩展规律
由于环境因素造成合金的表面损伤,因此小裂纹一般都是从腐蚀缺陷 (腐蚀坑或腐蚀层) 处萌生的.如Turnbull (2009)使用有限元模型描述了直径为100 μm 的腐蚀坑附近的应力和应变分布.研究发现最大应力位于腐蚀坑底部,但最大塑性变形位于腐蚀坑的开口附近.故在某些条件下,由于强烈塑性变形的存在,坑口附近也会发生裂纹的萌生.而腐蚀层由于造成合金表面的疏松而导致裂纹源于表面形成.有关燃气涡轮发动机热端部件的热腐蚀/氧化机理在我们之前的研究中(赵高乐等2022)进行了详细的解释.
如在铝合金等中所报道的那样(Shyam et al.2004),温度对小裂纹行为的影响是显著的.Stephens (1993)对Waspaloy 合金的研究表明,温度可以明显改变疲劳裂纹的形成、滑移特性以及裂纹的扩展速率.一般认为高温条件 (如燃气涡轮发动机热端部件的典型工作温度) 下,空气中的氧气导致的裂纹尖端状态的改变是控制裂纹扩展速率的主要因素之一,对应的机制为裂纹尖端材料的脆化和氧化诱发裂纹闭合(Chan et al.2014).此外,如前图8 中的小裂纹扩展结果所示,小裂纹扩展速率随温度升高而增加,这通常归因于材料强度的降低.
不同温度下,在镍基高温合金的疲劳小裂纹扩展过程中观察到不同的扩展模式.从室温到大约700 ℃的温度,镍基高温合金中的疲劳裂纹形成和早期生长往往是穿晶的.对于IN100 粉末合金,低于450 ℃的温度下,塑性变形主要通过沿八面体滑移面的平面滑移发生,导致{111}晶体学平面的裂纹生长(Li et al.2004).在中等温度下 (450℃~ 700 ℃),镍基高温合金中的两个{111}平面上可激活多个滑移系统,小裂纹倾向于沿垂直于加载轴的平面扩展(Bettge &Österle 1999,Phillips et al.2013).
针对单晶镍基高温合金,由于晶粒取向会引起小裂纹扩展行为的改变,故同一温度下合金可能会表现出不同的小裂纹扩展行为.Chen 等(2023)在高温环境下对CMSX-4 合金的裂纹扩展行为进行了系统的分析.如图23 所示,发现试样的取向和温度差异会引起裂纹扩展模式发生变化.高温下首先以垂直于加载方向扩展,随后转变为沿晶体学平面的扩展模式.Liang 等(2019)在NBSCS 的疲劳小裂纹扩展过程中观察到不同的扩展模式.室温下疲劳小裂纹以非结晶疲劳方式扩展.在700 ℃下,宏观观察时疲劳裂纹表现为晶体学扩展模式.随着温度上升到800 ℃和900 ℃,晶体扩展模式的比例逐渐从70%下降到37%.而随着温度达到980 ℃时扩展模式又增加到60%.
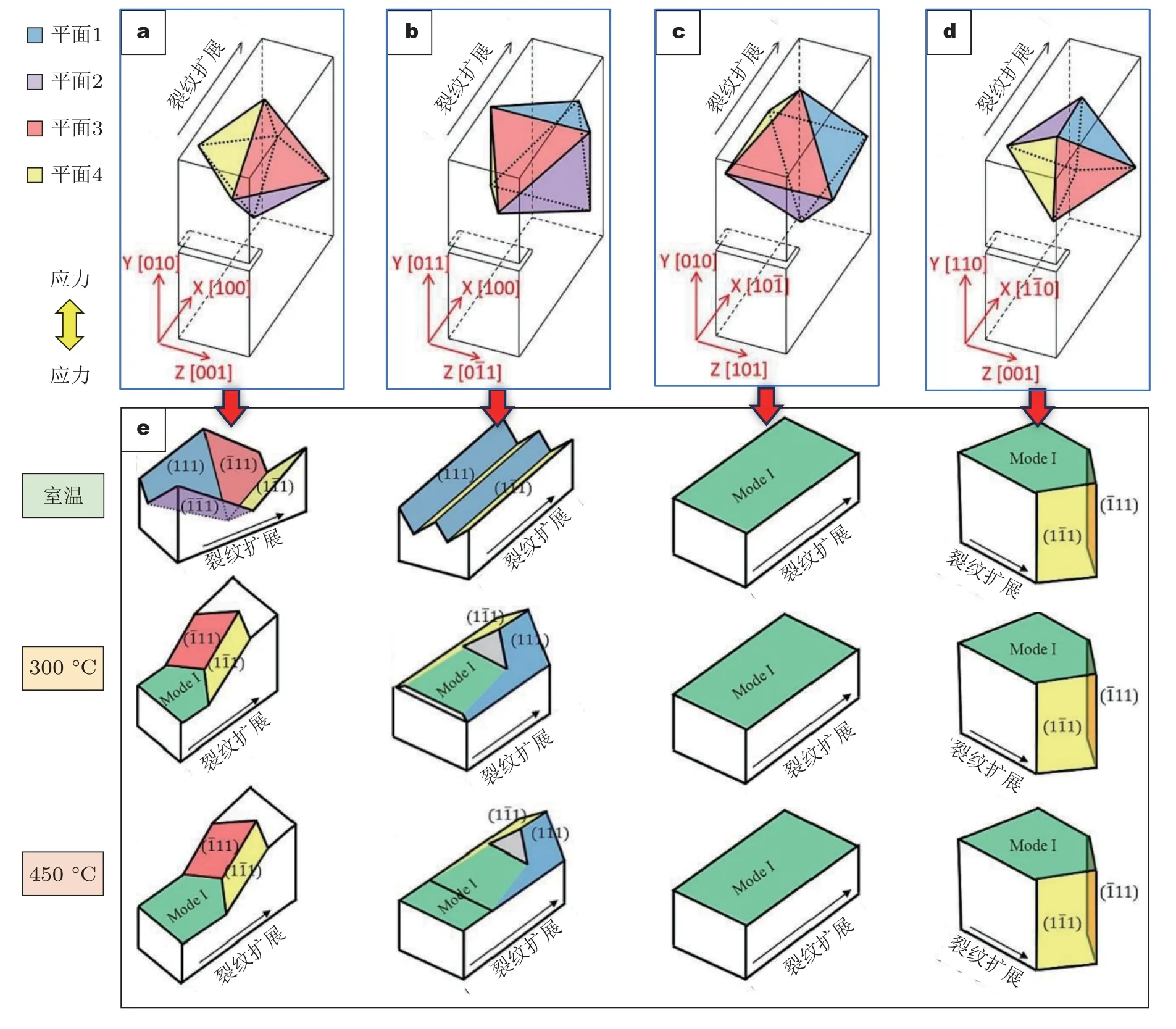
图23 不同取向的CMSX-4 合金在高温环境中的裂纹扩展模式(Chen et al.2023).(a)-(d)不同取向的试样,(e)不同温度下裂纹的扩展模式
腐蚀环境中的小裂纹扩展行为,除了受材料的化学成分、微观结构等影响之外,裂纹尖端腐蚀性元素的浓度同样是不可忽略的(Murtaza &Akid 1996).相关研究(Bache et al.1997,Ding et al.2009,Gaddam et al.2014,Sarrazin-Baudoux et al.2006)已经指出了气体环境种类对钛合金疲劳行为的影响.与空气相比,真空中的Ti-6Al-4V 和Ti-6246 合金疲劳裂纹萌生发生了延迟(Demulsant &Mendez 1996).
在腐蚀环境中合金表面形成的氧化物层性质严重影响疲劳裂纹扩展速率,如图24 所示.另一方面,在晶界处停止的裂纹会随着腐蚀环境的引入而立即重新开始扩展(Geathers et al.2022).这种增强的滑移活动,以及可能激活的多个滑移系统,造成相同长度的疲劳裂纹在惰性环境中比在腐蚀环境中能够承受更多的循环.对于给定的ΔK,氧化物碎屑通过提高裂纹闭合水平Kcl从而降低了有效裂纹扩展驱动力ΔKeff.同时,化学元素对裂纹尖端局部区域的扩散会严重损伤裂纹尖端附近的材料,受损材料不再代表原始材料.在循环应力作用下裂纹尖端的局部塑性变形暴露了基体金属,从而导致腐蚀产生额外的裂纹扩展增量.经过一段时间后,裂纹尖端随着膜的增厚而重新钝化,金属溶解得到缓解.随后,在膜厚度和累积应变的组合下这一过程重复进行.因此,腐蚀环境的中材料的裂纹扩展速度加快.

图24 腐蚀疲劳小裂纹及其腐蚀层形貌
在对铸造铝合金中小裂纹扩展行为的研究中,Zhu 等(2008)还发现湿度会显著增加疲劳裂纹扩展速率.腐蚀与空气条件下的小裂纹扩展速率如图25 所示.所示.相对于空气中的裂纹扩展速率,在相同的ΔK值范围腐蚀环境中的疲劳裂纹生长速率都增加了约10 倍.凹坑处的裂纹萌生也表现出对环境的强烈依赖性,观察到空气中的萌生寿命比真空中短.Piascik (1999)对7075铝合金表面腐蚀疲劳小裂纹扩展特性进行了系统的研究,结果发现暴露在NaCl 溶液中的小裂纹扩展速率约增加了3 倍.Chanyathunyaroj 等(2020)发现3.5%NaCl 溶液会在6061 铝合金表面产生腐蚀坑,在疲劳加载期间腐蚀坑的存在会迅速促进小裂纹的形核,是导致部件提前失效的重要因素.
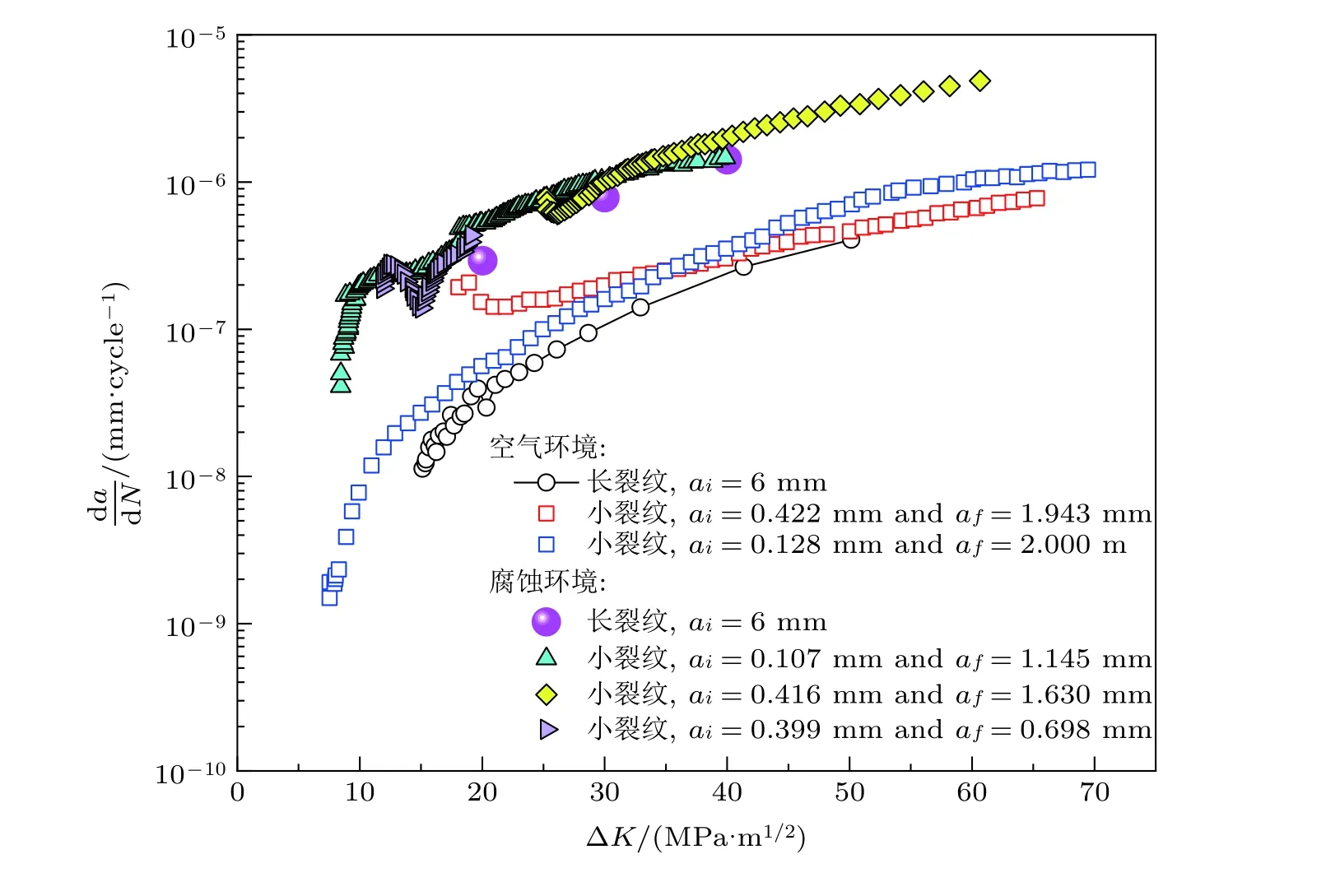
图25 汽轮机叶片钢FV566 在空气和腐蚀环境 (90 ℃: 300 × 10-9 Cl-+300 × 10-9 ) 中的小裂纹和长裂纹扩展速率(Turnbull &Zhou 2012)
图26 是恒幅应力范围下不同腐蚀坑深度的疲劳裂纹扩展速率.发现在裂纹扩展的早期阶段,裂纹扩展速率表现出加速和减速行为.此外,腐蚀坑尺寸对裂纹扩展的影响也很明显,即腐蚀坑越深,裂纹扩展速率越高.在裂纹扩展的后期阶段,无论试验条件如何,疲劳裂纹扩展很少发生波动甚至不会发生波动,疲劳裂纹扩展速率似乎随着裂纹长度的增加而线性增加 (遵循相似的斜率),直到发生破坏.进一步观察图26 表明疲劳裂纹扩展曲线在腐蚀坑尺寸达到一定程度后会发生收敛,故在此阶段开始腐蚀坑尺寸对疲劳裂纹扩展的影响可以忽略不计.
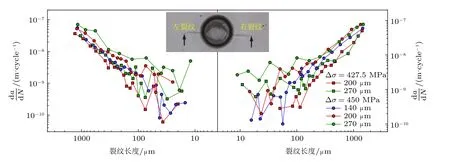
图26 不同腐蚀坑尺寸下,X65 钢的裂纹扩展速率与裂纹长度的关系图(Fatoba &Akid 2022)
在应用门槛值概念进行设计时必须非常谨慎,对于小裂纹来说尤其如此.这是因为对于疲劳小裂纹来说,虽然施加的K值可能非常低但还是可能会发生扩展.影响小裂纹行为的一个力学因素是塑性区尺寸可能与裂纹尺寸相当,这使得线弹性断裂力学失效.即使在裂纹驱动力中考虑了塑性区效应,断裂力学相似性也可能不适用于裂纹早期阶段的生长.对于给定的材料和环境,在小裂纹状态下力学和化学因素都会使裂纹在门槛值以下扩展.
Mille (1987)得到环境中的小裂纹扩展具有以下规律: (1) 腐蚀环境降低了线弹性断裂力学门槛值并增加了疲劳裂纹扩展速率;(2) 腐蚀环境中小裂纹扩展的障碍更容易被克服;(3) 在真空中因为更大的阻力,在产生主裂纹之前的时间间隔更大.即在固定表面面积内会产生更多的裂纹,且主要为深度仅为一个晶粒的晶间裂纹;(4) 点蚀对疲劳性能的影响还表现为对小裂纹扩展的加速效应,这些小裂纹的形核是由于腐蚀环境中的腐蚀坑而形成的.最后,当足够多的小裂纹形核生长至临界尺寸时便开始了长裂纹的扩展.然而,目前针对环境因素对小裂纹扩展行为影响的研究还相对较少.受限于高温环境中的试验方法,对热腐蚀环境中的小裂纹扩展研究还不够系统详细,特别是在氧化/热腐蚀对小裂纹扩展的作用机制方面研究还不够深入,多数研究仍只能回答环境因素对小裂纹扩展的影响结果.
5.3 腐蚀疲劳小裂纹萌生机制
由3.2 节可知,空气中VHCF 的裂纹通常遵循内部萌生机制.微观小裂纹在低应力幅下产生,通常很难用传统的无损检测方法检测出来.因此在循环应力作用下疲劳小裂纹可以缓慢发展直至达到临界尺寸,最终导致合金的断裂.然而,在腐蚀环境介质中,VHCF 裂纹萌生机制会有所不同.首先,腐蚀性介质的存在会加速材料表面微观小裂纹的形成.其次,由于机械载荷和材料表面化学侵蚀之间的相互作用,会发生腐蚀疲劳.腐蚀产物会累积并起到应力集中的作用,导致小裂纹快速产生.最后,腐蚀介质还会加速疲劳小裂纹的扩展.总之,VHCF 中的裂纹萌生机制受到材料的微观结构、化学成分和表面光洁度的显著影响.
在腐蚀性环境中,金属表面由于腐蚀或侵蚀而发生劣化,导致形成腐蚀坑或腐蚀层.由于应力集中效应,小裂纹可以从表面腐蚀层或腐蚀坑位置处开始,即使是一个极低的循环荷载也会导致金属表面小裂纹形成.故腐蚀环境的存在有助于小裂纹的形成.一旦小裂纹形成,它们可以在循环载荷下扩展,直到达到临界尺寸并扩展成长裂纹.同时,在腐蚀性环境中,腐蚀性物质的存在会弱化金属的性能从而加速裂纹扩展.当裂纹达到临界长度,材料不再能承受施加的循环载荷时,最终发生断裂.值得注意的是,腐蚀环境中VHCF 的裂纹萌生和扩展过程高度依赖于材料的微观结构和暴露环境的腐蚀性.在VHCF 区域,表面和内部缺陷对裂纹萌生的竞争是一个不变的因素.然而,腐蚀的表面导致疲劳裂纹优先萌生的位置数量显著增加,从而增加了表面裂纹产生的可能性.而高温环境形成的氧化层在低应力载荷下不易发生破坏,从而起到了一定的保护作用.这将导致VHCF 的裂纹依然在合金内部引发.
观察预腐蚀R5 钢样品的纵向截面,如图27(a)所示,经过4.37 × 108次循环后在腐蚀坑处有小裂纹形成,该初始疲劳裂纹从表面半球形腐蚀坑引发并沿垂直于加载方向扩展.而在图27(b)中,经过热腐蚀预处理后,IN718 合金的疲劳寿命为2.97 × 106.在断裂样品的纵向截面中很明显地看到,疲劳裂纹从劣化的表面开始并呈现出多源萌生模式.故预热腐蚀加速了IN718 合金的疲劳损伤过程,降低了其疲劳寿命.图27(c)和图27(d)表明即使在高温环境中有氧化层形成,仍然观察到疲劳裂纹于合金内部的缺陷处萌生.这是因为VHCF 下外加载荷较低,无法对氧化膜造成破坏,从而内部因素竞争超过表面因素,疲劳裂纹从合金内部萌生并发生扩展.

图27 (a)VHCF 下R5 钢腐蚀坑处的疲劳裂纹萌生(Pérez-Mora et al.2015),(b) HCF 下IN718 合金腐蚀层处的疲劳裂纹萌生(Pradhan et al.2018),(c) VHCF 下铸钢G42CrMo4 在500 ℃环境中的断裂表面和(d)裂纹萌生位置放大图(Schmiedel et al.2020)
总之,腐蚀环境会诱导合金表面形成腐蚀层和腐蚀坑,造成合金表面状态的劣化,对小裂纹的产生和扩展速率产生显著影响,从而影响材料的疲劳寿命.此外,材料表面的小裂纹萌生呈现出多源萌生模式,这些裂纹可以相互作用并合并成更大的裂纹,导致裂纹萌生过程变得更加复杂.
5.4 腐蚀疲劳小裂纹扩展模型
为有效避免腐蚀疲劳小裂纹扩展阶段的复杂和理论建模的困难,Zhang 等(2021)基于等效初始缺陷尺寸的概念将腐蚀坑的形成、生长以及小裂纹扩展过程囊括进长裂纹扩展过程提出了一种改进的疲劳寿命预测模型.Rémy 等(2013)用过程区理论描述小裂纹扩展并提出了耦合氧化影响的裂纹扩展速率方程.
这些缺陷或小裂纹尺寸依赖于应力强度因子门槛值水平,而对于较长的裂纹,ΔKth变成材料常数,它等于长裂纹的疲劳裂纹门槛值范围ΔKth,lc.通过将方程中的ΔKth等效为ΔKth,lc,可以如下估算到长裂纹的过渡尺寸.Turnbull (2013)在腐蚀环境中 (模拟冷凝水) 测量汽轮机材料的小裂纹扩展速率,其中概述了对小裂纹扩展行为的研究(Turnbull 2017),以表征环境辅助裂纹扩展的早期阶段,重点是裂纹萌生前的性质,坑到裂纹的转变,以及化学溶液对小裂纹和长裂纹范围内扩展速率的影响.Balbín 等(2021)通过微观力学模型研究了疲劳小裂纹从腐蚀坑扩展的能力 (坑到裂纹的转变).凹坑的几何形状、裂纹和微观结构障碍是用分布位错模拟的.该模型考虑了局部凹坑形状的影响,并通过特定环境中材料的Kitagawa-Takahashi 图考虑了环境对小裂纹和长裂纹扩展的影响.
Akid 和Miller (1991)对Brown-Hobson 模型(Hobson et al.1986)和Navarro-de los Rios 的理论模型(Navarro &de los Rios 1988)进行简单修改得到了腐蚀环境下小裂纹的扩展模型.包含一个表示金属溶解腐蚀过程.在小裂纹扩展方程中加入溶解项的主要效果是,由于引入了裂纹扩展增量 (作为金属溶解过程发生),小裂纹不会发生停止效应
Brown-Hobson 推导出的模型考虑了达到和超过主要微结构障碍两种基本状态下的小裂纹生长
式中,A、B、α和β表示材料常数;Δγ是剪切应变范围,a为裂纹长度,d为微结构障碍间距,而D代表应力相关的裂纹扩展速率阈值.另一方面,基于连续分布位错理论Navarro 和de los Rios 提出了相应的小裂纹扩展模型
式中,系数f与活动滑移带上的位错数量有关,而φ是裂纹尖端塑性位移的量度,n是裂纹长度与塑性区尺寸的比值.将腐蚀造成的溶解效应耦合进式(35)或式(36),如模型(34)就可以得到腐蚀环境中小裂纹的扩展速率模型,其中
式中,icorr是金属溶解的阳极电流密度,ω是频率,z、F、M和ρ为常数.
在线弹性断裂力学参量ΔK下小裂纹的生长速率显著高于长裂纹,故使用长裂纹模型来分析小裂纹扩展通常会导致非保守的寿命估计.上述第一个腐蚀疲劳小裂纹扩展模型是基于缺陷处的裂纹扩展研究,将腐蚀坑近似为一般缺陷,这忽略了扩展过程中腐蚀介质对裂纹尖端的影响,故会对腐蚀疲劳小裂纹扩展速率造成危险的估计.而第二个模型只是在数学表达式内将总的扩展速率拆分成了单纯由力学效应造成的裂纹扩展和腐蚀介质造成的额外扩展,其无法体现腐蚀疲劳小裂纹扩展过程中的复杂机制,如环境和力学之间的相互促进作用.此外,这两种模型都是基于室温环境中的一般腐蚀,尚未发现高温环境中的腐蚀疲劳小裂纹扩展模型研究,其对于燃气涡轮发动机热端部件热腐蚀疲劳的适用性有待于进一步验证.
同时,环境因素会加剧小裂纹效应.根据K方法建立的小裂纹扩展行为代表材料从长裂纹产生的稳态疲劳裂纹扩展速率响应,当应用于加载历史时,可能导致非保守的寿命估计.目前来说,针对镍基高温合金材料的腐蚀疲劳小裂纹扩展行为的研究较少,且存在许多尚待解决的问题.首先,对于腐蚀疲劳小裂纹扩展的力学机制尚未完全明白,如环境引起的裂尖微观形貌改变对裂纹扩展的作用等;其次,小裂纹的扩展严重依赖于初始缺陷形状、晶粒尺寸等材料微结构特征,具有很大的不确定性,使得寿命预测值具有很大的不确定性;最后,在高温环境和复杂机械载荷作用下,裂纹尖端的应力分布将出现复杂的变化,如应力松弛等.总之,当前对于空气中的疲劳小裂纹扩展寿命预测研究取得了较好的效果,但腐蚀环境下的小裂纹扩展机制尚不清楚,因此,需要借助先进手段并开发更加完备的研究方法进行腐蚀疲劳小裂纹研究以得到更加精确的小裂纹扩展模型,进而发展出适应于我国燃气涡轮发动机的热端部件抗腐蚀疲劳寿命设计方法.
6 小裂纹研究结论与展望
6.1 结论
本文围绕近年来对疲劳小裂纹的研究成果,系统综述了当前疲劳小裂纹的扩展规律、机理、对疲劳寿命的影响以及扩展模型.主要有以下结论.
(1) 虽然当前针对小裂纹的定义以及划分尺度存在争议,但基本达成了共识,即小裂纹由微观小裂纹、力学小裂纹以及物理小裂纹组成.根据不同材料类型微观组织的不同划分尺度略有差异,且一致认为在小于约1 mm 的尺寸范围内会出现小裂纹效应.
(2) 受应力水平、试验环境、应力比以及材料类型等因素的影响,疲劳小裂纹扩展阶段对总寿命的占比存在较大范围的分散 (20%~ 90%),说明在材料的疲劳损伤演化过程中疲劳小裂纹阶段是不可忽视的.
(3) 从LCF 到HCF、VHCF 寿命区域,裂纹逐渐倾向于内部萌生,同时,由于疲劳裂纹萌生机制不同,造成S-N 曲线呈现出多阶段特征.
(4) 疲劳小裂纹扩展行为受材料的微观结构、施加载荷以及外部环境共同主导.对于多晶合金,其波动效应主要是由于晶界、夹杂以及气孔等微观组织引起的;对于单晶合金,疲劳小裂纹扩展行为主要与加载过程中产生的滑移带密切相关.同时,由于塑性诱导的裂纹闭合效应导致实际的裂纹扩展驱动力升高,造成疲劳小裂纹扩展加速且在低于长裂纹扩展门槛值的情况下仍能扩展.
(5) 热腐蚀形成的腐蚀层和腐蚀坑诱导疲劳小裂纹的萌生;同时,在腐蚀环境和疲劳载荷共同作用下,外部环境的腐蚀元素会扩散至裂纹尖端,导致裂纹尖端区域的应力分布发生变化.因此,腐蚀介质会加快小裂纹的萌生和扩展.
6.2 展 望
为了更加准确地评估燃气涡轮发动机关键部件的耐久性,保障飞行安全需要对疲劳小裂纹问题进行更加深入的研究.对于未来相关研究,笔者提出了粗浅的看法.
(1) 一般来说,疲劳小裂纹的扩展严重依赖于初始缺陷、晶粒以及晶界等材料的微观组织,故可以用来描述导致小裂纹扩展波动的微观结构不均匀性.但燃气涡轮发动机涡轮叶片常用材料,如镍基单晶高温合金不存在晶界且存在力学各向异性,其他微观组织 (如孔隙、夹杂、碳化物等) 和取向如何共同主导小裂纹扩展行为,需要进一步的探究.
(2) 对于燃气涡轮发动机涡轮叶片、涡轮盘等关键部件来说,受到的疲劳载荷形式比较复杂,因此,小裂纹是否会影响关键部件HCF、VHCF 等性能,有待进一步研究.
(3) 当前对腐蚀疲劳小裂纹行为的研究仅仅局限于室温环境中,在高温条件下尚无法清晰地捕捉小裂纹扩展规律.甚至国内外构建的腐蚀疲劳小裂纹扩展模型均没有对其复杂力学的化学机制进行描述,这严重影响当前的研究成果在燃气涡轮发动机热端部件中的应用.故应进一步发展合适的热腐蚀疲劳小裂纹扩展试验方法.
(4) 如何准确量化腐蚀疲劳小裂纹扩展行为是正确预测腐蚀疲劳寿命的前提.因此,亟待从微观尺度弄清楚小裂纹扩展的控制参量 (能够同时兼顾力学和化学机制),进而建立符合腐蚀疲劳小裂纹扩展机制的描述模型.
致 谢国家自然科学基金资助项目(51975027).
