结构状态识别与评估的机器学习方法研究进展

2023-02-24鲍跃全

力学进展 2023年4期

黄永鲍跃全李惠

哈尔滨工业大学土木工程学院,150090 哈尔滨

1 引言

结构健康监测通过在大型基础设施上布置传感器,现场感知、识别和诊断结构的健康状态,已经成为保障基础设施服役安全的重要途经.结构健康监测多源异构数据蕴含着丰富的结构信息,如何挖掘这些信息,进行结构的状态识别、诊断与评估是结构健康监测的核心科学问题 (李惠等 2015).土木工程结构规模大、尺度大、构造复杂,通过监测数据识别和评估结构状态是具有挑战的难点问题.结构状态识别与评估本质是反问题,同时也是高维问题,国际上在该方向开展了三十余年的研究,取得了大量的研究成果 (Sohn et al.2003,Bao et al.2019).但结构状态识别和评估的准确性方面仍需进一步提升,近年来,随着人工智能、大数据与机器学习理论与技术的发展,结构健康监测从基于振动数据的范式转向基于机器学习的大数据范式 (Bao &Li 2021),机器学习能自动从海量监测数据中学习到隐含的结构健康特征实现状态识别与评估,在高维问题求解方面的能力引起国内外学者的关注,也在结构健康监测机器学习方面进行了大量的研究,建立的机器学习方法在准确性和抗噪性、智能化等方面均具有明显的优势.

本文聚焦近年来机器学习在结构模态识别、损伤识别及可靠性评估等方面的研究成果,首先介绍结构模态识别的机器学习方法,讨论稀疏贝叶斯学习与深度神经网络在结构损伤识别中的应用研究进展;然后,介绍基于监测数据的结构可靠性评估机器学习方法,主要包括基于机器学习的结构可靠度计算方法和结构系统失效模式搜索与识别;最后探讨结构状态识别与评估的未来发展趋势.

2 结构模态识别的机器学习方法

结构模态参数 (频率、振型、阻尼比) 是了解结构状态、识别和诊断结构健康的重要指标.结构线性模态的识别的发展相对比较成熟,形成了较为系统的理论和方法体系.在土木工程结构健康监测中,常用环境激励性的模态识别方法,如FDD、随机子空间方法、NExT-ERA 方法等.上述方法本质上是基于特征矩阵分解的思想,从构造的特征矩阵中分解得到特征值和特征向量.在实际应用中,由于测量噪声的存在,矩阵分解常存在虚假的特征值,也即虚假模态.为了剔除虚假模态的干扰,往往需要进行人为的参数设定或模型定阶,难以满足结构健康监测系统实时自动分析数据的需求.如何通过机器学习的方式,从监测数据中自动获取模态参数是值得研究的问题.目前基于机器学习的结构模态参数识别方法主要包括: 基于计算机视觉的方法、采用机器学习优化求解模态方程的方法、机器学习和随机子空间方法,以及基于机器学习的后处理方法等.

基于计算机视觉的结构模态参数识别方法,主要利用计算机视觉技术结合盲源分离方法从结构振动的视频图像中得到结构模态参数.Yang 等 (2017a,2017b) 研究利用欧拉影像放大法提取结构振动视频中每一帧的相位信息,通过相位信息得到结构振动的位移信息,然后结合盲源分离中的复杂度追踪算法得到结构的模态参数 (图1).随后,Yang 等 (2020a) 提出了一种基于卷积神经网络和长短期记忆网络的结构模态频率识别方法,该方法利用卷积神经网络提取视频中每一帧的振动特征,然后利用长短期记忆网络建立不同时刻振动特征与模态频率的映射关系.另外,Zhou 等 (2021) 引入全息视觉传感技术开发了一种基于视觉的结构模态参数识别方法,建立能描述结构几何形态的特征点集,获取结构的动力学行为特征,实现结构模态参数的定量分析.Lu 等 (2021) 建立了一个基于视觉模态分析的框架来识别结构模态参数,该方法在微幅振动和一定光滑性的假设下将结构模态参数与视觉数据直接关联,通过频域分解进行视觉模态分析并获取结构模态参数.

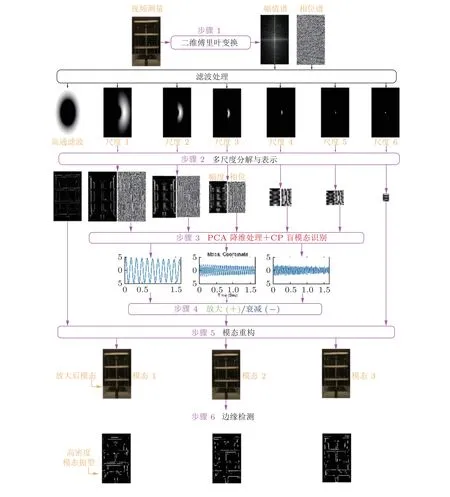
图1 基于计算机视觉的结构模态参数识别方法 (Yang et al.2017a)

采用机器学习优化求解模态方程的方法,将模态参数求解问题转化为机器学习中神经网络对目标函数的优化问题.将模态参数求解的数学原理嵌入到神经网络中,如图2 所示,Liu 等(2021) 提出了基于模态独立性的结构模态参数机器学习求解方法.该方法利用环境激励下结构模态响应相互独立的特点,将衡量独立性的指标嵌入到神经网络目标函数中,利用机器学习优化能力实现对模态响应和振型的求解.

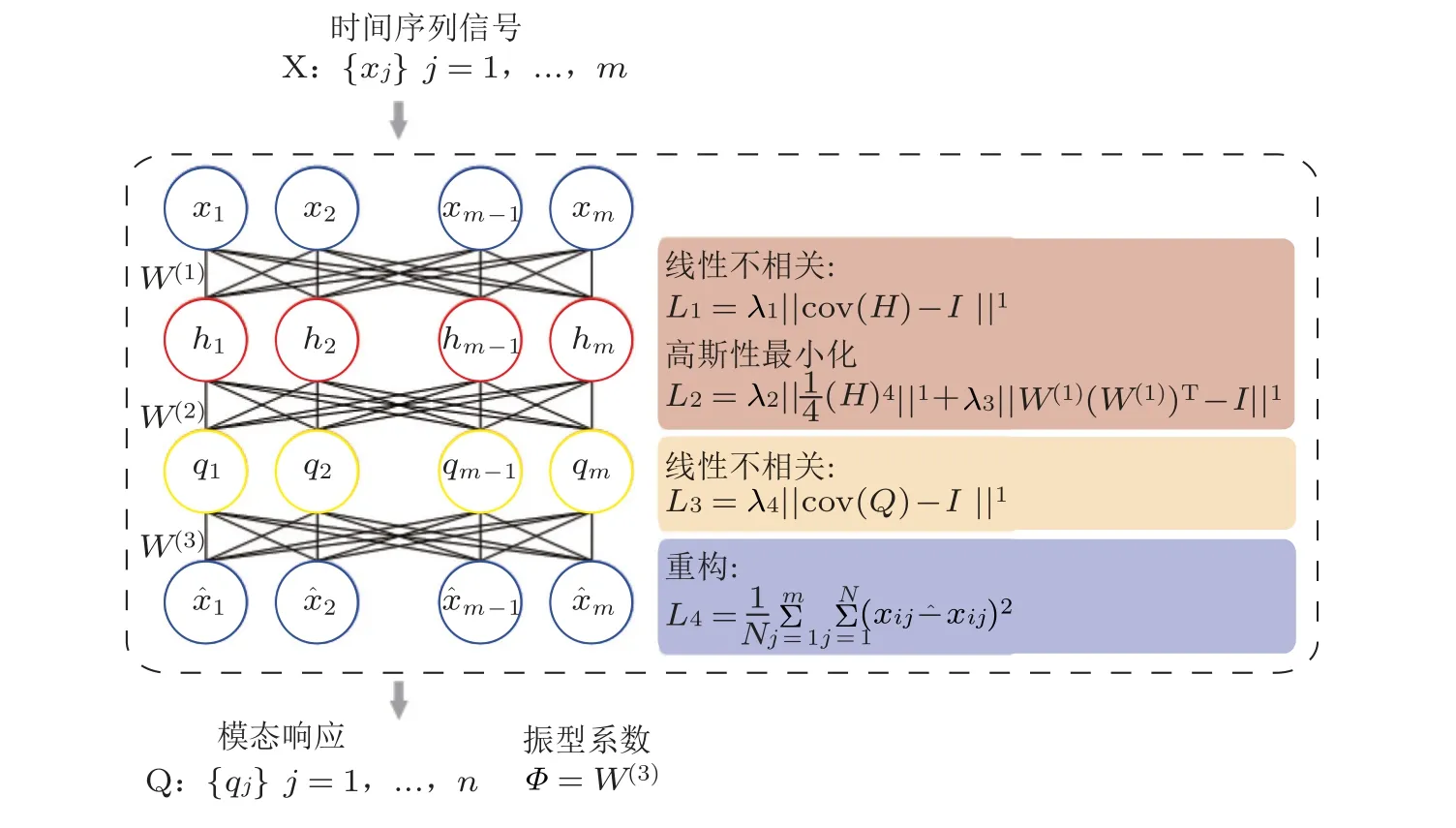
图2 基于模态独立性的结构模态参数机器学习求解方法 (Liu et al.2021)

在随机子空间和机器学习结合方面,Su 等 (2020) 通过融合随机子空间识别的不确定性量化和深度卷积神经网络,实现了结构模态参数的自动识别.利用虚假模态的不确定性明显大于真实物理模态的不确定性的特点,采用卷积神经网络 (CNN) 自动分析不确定性图,有效识别了结构物理模态.此外,Liu 等 (2023) 提出利用模型定阶网络和模态参数识别网络来求解模态参数,如图3 所示,所提出的模态参数识别网络包括两个子网络: 模型定阶网络和模态参数识别网络.在模型定阶网络中,将Toeplitz 矩阵 (由输出的协方差矩阵得到) 奇异值分解得到的奇异值作为网络的输入,利用设计的损失函数可以自动确定模型的阶次.在模态参数识别网络中,将随机子空间方法的原理嵌入到神经网络中,利用设计的损失函数可以得到系统矩阵和观测矩阵.

图3 基于机器学习和随机子空间的结构模态参数识别方法 (Liu et al.2023)

基于机器学习的传统模态参数识别的后处理方法,利用机器学习的聚类、主成分分析等方法对随机子空间方法得到的模态参数进行进一步处理,得到较为正确的模态参数作为最终的结果,减少虚假模态的影响.如图4 所示,Fan 等 (2019) 提出了基于随机子空间和聚类方法的结构模态参数自动识别方法,该方法对随机子空间方法求解得到的模态参数利用聚类进行进一步处理,去除其中虚假模态,实现模态参数的准确自动识别.Mao 等 (2019) 提出了基于主成分分析和聚类方法的结构模态参数自动识别方法,该方法对随机子空间方法等方法求解得到的模态参数利用主成分分析和聚类进行进一步处理,得到更加准确的模态参数,实现模态参数的准确识别.Demarie 和Sabia (2019) 提出了一个健康监测自动化的总框架,包括模型阶次选择与验证、系统识别、聚类和自动监测四个步骤.Facchini 等 (2014) 利用和结构频率相关的四个指标作为神经网络的输入来识别结构模态参数.

图4 结构模态参数聚类结果 (Fan et al.2019)

基于机器学习的结构模态识别方法相对于传统方法,解决了传统方法由于测量噪声的存在,难以准确自动定阶,导致识别结果中包含虚假模态,降低了识别的精度的问题.基于机器学习的结构模态识别方法将模态定阶和模态识别自动嵌入到机器学习中,实现网络的训练过程就是模态参数定阶求解过程,将模态参数的定阶求解问题转化为网络的优化问题,利用机器学习强大的优化能力,实现模态参数的自动定阶求解.在实际监测数据应用中具有避免过多人为参与,降低虚假模态干扰的优势,可集成到结构健康监测系统中实现自动识别.

3 基于监测数据的结构损伤识别的机器学习方法

结构模态识别为损伤识别提供了丰富的结构振动特征信息,这些模态信息与结构损伤相关的刚度、质量和阻尼等物理特性具有直接的联系.基于模态等监测数据信息进行结构损伤识别是结构健康监测的核心科学问题之一,近年来发展起来的基于机器学习的结构损伤识别方法主要包括: 基于稀疏贝叶斯学习的方法和基于深度卷积神经网络的方法.

3.1 基于稀疏贝叶斯学习的结构损伤识别方法

基于模型反演的结构损伤识别,主要通过结构模态参数反演结构刚度参数,实现结构损伤识别

式中,K和M分别对应结构刚度和质量矩阵,ε为测量误差.

在实际应用中,结构损伤识别反问题往往受到不同来源不确定性因素的影响,包括: 测量信息空间不完备、测量噪声、结构模型误差、环境干扰等.当采用含噪且不完备的健康监测数据时,损伤识别反问题往往存在病态和不适定性、解不唯一和结果不鲁棒等问题.因此,在计算过程中,描述模型参数基于观测数据的所有可能取值具有良好的意义,贝叶斯概率方法为解决此问题提供了强大的计算工具.此外,损伤识别中不可避免存在推断损伤位置的空间分辨率和损伤推断的可靠性之间存在的平衡,即结构局部布置的传感器网络提供的数据信息通常不足以支撑构件级别损伤识别,缓解这一问题的重要策略是尽可能多地纳入先验知识,以约束解空间;例如,损伤空间稀疏性的先验知识特别有效,即在结构没有倒塌的情况下,结构刚度因损伤而变化通常发生在结构中的有限位置.最近,利用此先验知识,发展了一系列基于模型稀疏反演的损伤识别方法,例如l 范数正则化最小二乘方法 (Hou et al.2019) 和稀疏贝叶斯学习方法 (Huang &Beck 2015,Huang et al.2017b,Huang et al.2020,Hou et al.2020),已被验证可以产生更鲁棒的结构损伤识别结果,也可实现更高分辨率的损伤定位.本节主要介绍稀疏贝叶斯学习的结构损伤识别研究进展.

为了进行基于稀疏贝叶斯学习的结构损伤识别,Huang 和Beck (2015) 建立了图5 所示的层次贝叶斯模型,其中箭头代表条件相关性.在图中,ω2和φ分别表示系统固有频率和振型,对应识别频率ωˆ2和振型ψˆ 数据.基于此模型可定义基于结构刚度参数θ、系统模态参数ω2和φ的联合先验概率密度函数

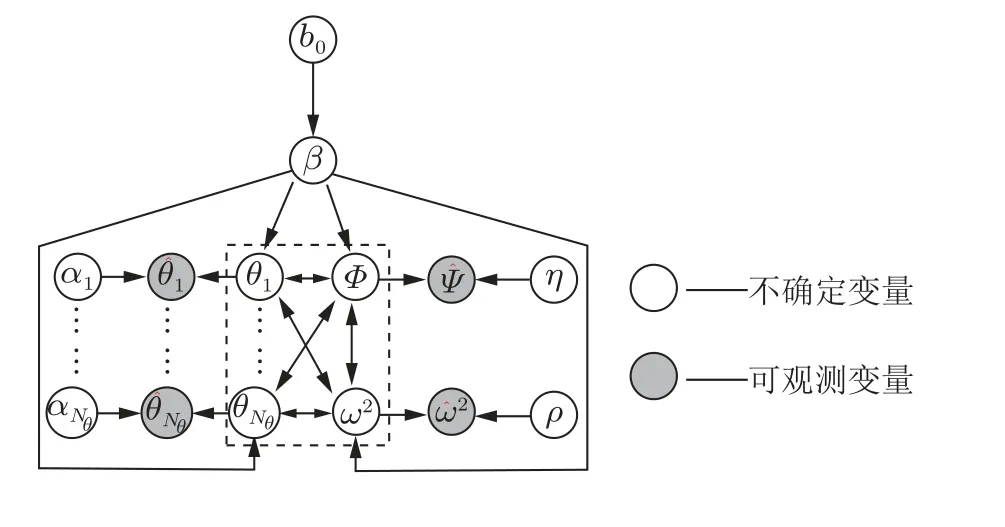
图5 结构损伤识别问题的层次贝叶斯模型

式中,β为方程误差精度参数,控制系统模态参数和模型模态参数的一致程度.为了嵌入刚度变化的空间稀疏性,选择结构基准状态刚度参数值作为θ的伪数据,定义刚度参数的似然函数如下

如果超参数αs→0,则θs→,即第s个子结构未受损伤.实际大部分子结构单元未损伤,因此对应的很多超参数αs→0 .

基于图5 所示的层次贝叶斯学习模型,Huang 等 (2017a) 提出了快速稀疏贝叶斯学习算法,该算法专注于刚度参数θ的后验概率密度函数的计算,并将所有其他不确定参数δ=视为“冗余”参数.采用拉普拉斯近似,刚度参数θ的后验概率密度可近似为

为了更全面地量化模型参数的后验不确定性,Huang 等 (2017b) 研究了基于吉布斯采样的稀疏贝叶斯学习结构损伤识别方法,通过将整个模型参数向量分解为四个参数组并基于其他三组参数和数据推导获得每一参数组的条件后验概率分布的解析解,对应超参数都基于数据直接学习得到.利用吉布斯采样对各个条件后验概率分布连续采样获得后验样本.整个方法有效维数为4,相对于模型参数的总维度要明显降低.图6 为刚度参数的后验分布样本,在θ1,-y对应的结构单元,刚度的概率分布分散在一个较大的范围内,且大部分概率密度对应的刚度系数小于1,表明此单元发生损伤;但在大部分单元,概率分布集中于1 附近,表明未发生损伤.此方法实现了较明确的损伤定位,减少了损伤误判.

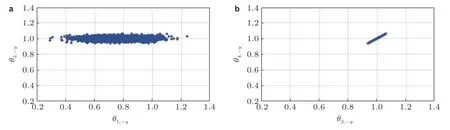
图6 结构损伤识别吉布斯采样的后验分布样本.(a)某损伤单元和未损伤单元刚度参数的联合后验分布样本,(b) 某两个未损伤单元刚度参数的联合后验分布样本

此外,Huang 等 (2020) 进一步研究了引入更多结构损伤先验物理信息来提升损伤识别的反演精度,例如结构损伤引起的刚度损失除了每一时刻具有空间稀疏性以外,其随着时间的变化也具有稀疏性的先验信息.将贝叶斯机器学习与双卡尔曼滤波器结合,建立了动态稀疏系统的双卡尔曼滤波方法,实现结构状态和刚度参数的联合在线估计.该方法具有卡尔曼滤波噪声参数自动学习的优点,提高了滤波结果的鲁棒性和准确性.近几年来,更多稀疏贝叶斯学习的结构损伤识别方法被相继提出: Hou 等 (2020) 在基于振动监测数据的稀疏贝叶斯学习损伤识别中融入了环境温度对结构振动特性的影响;Wang 等 (2022) 构建一个新的结构损伤指数,并以通过健康状态的结构数据建立稀疏贝叶斯学习回归模型作为基准,通过监测数据下的损伤指数的偏移作为识别结构损伤的依据;Xie 等 (2023) 将拉普拉斯先验概率模型引入到稀疏贝叶斯学习损伤识别和不确定性量化中,获得了更高的计算效率并降低了对数据集的限制.

相对于传统结构损伤识别,稀疏贝叶斯方法通过损伤模型的稀疏化可实现结构损伤位置的明确指引,而无需人为阈值的设定.且稀疏贝叶斯学习过程自动嵌入了贝叶斯剃刀原理 (Beck 2010),能在获得稀疏损伤模型的同时有效避免数据的过拟合问题,抑制损伤误判和漏判的发生.此外,损伤识别结果的后验不确定性也有效表征了识别的置信度.

3.2 基于深度神经网络的结构损伤识别方法

深度神经网络由于其优越的特征学习能力,在土木结构损伤识别方面取得了一定研究进展.Lin 等 (2017) 较早提出了基于深度卷积神经网络的结构损伤识别方法,从原始传感器监测数据中自动提取特征,在无噪声和有噪声的数据集上均实现了出色的损伤定位精度.此外,对深度卷积神经网络中隐藏层学习的特征进行可视化,一定程度实现了对深度网络工作方式的物理解释.Feng 等 (2019) 提出了一种具有迁移学习能力的深度卷积神经网络的结构损伤识别方法,通过对高清摄像机获取的结构图像进行预处理后,采用迁移学习来训练Inception-v3 神经网络以检测损伤.Yu 等 (2019) 研究了带有控制装置的建筑结构损伤检测.建立的深度卷积神经网络能够从原始信号或低层次特征中自动提取高层次特征,并优化选择提取特征的多层融合.李雪松等 (2019)采用卷积神经网络直接从加速度信号自动提取特征并进行分类,具有对损伤敏感、计算简单、有一定抗噪能力的优点.Oh 等 (2020) 通过卷积神经网络表征健康状态下建筑结构动态响应的相关性,通过受损状态对应的网络预测输出与健康状态下真实响应的残差定义了损伤指标,缓解了需要采用大量带有损伤信息的结构响应进行卷积神经网络训练的难题.Wang 等 (2021a) 引入稠密卷积网络 (DenseNets),在卷积神经网络架构中实现了稠密连接,用于基于振动的结构损伤识别 (图7).学习和重复利用了低层和高层特征,不仅简化了训练过程中的信息流,还保留了所有级别的特征.此外,密集连通性缓解了梯度消失问题,并加强了特征在网络中的传播,这些特点可更有效应用于结构损伤识别.Lieu (2022) 等采用卷积神经网络,结合逆有限元法训练基于应变模态差异的损伤识别模型,该方法在不同的损伤条件下,具有显著的损伤定位能力和有较高的损伤量化精度.Lei 等 (2021) 提出将基于小波变换的结构响应传递率数据作为深度卷积神经网络的输入,利用小波传递性消除不同地震激励的影响.Chen 等 (2021) 结合连续小波变换和深度卷积神经网络,建立了一种传感器数据驱动的结构损伤检测方法,深度卷积神经网络被用来挖掘在基于连续小波变换获得的传感器信号的时频图像中的结构损伤特征,并区分各类损伤情况.He 等 (2021) 利用快速傅里叶变换从结构振动数据中提取结构频率信息,并基于深度卷积神经网络识别结构损伤状态.Abdeljaber 等 (2017) 研究了具有固有的自适应设计的一维卷积神经网络,将特征提取和分类块融合到单个紧凑的学习体中,通过处理由加速度计采集的原始振动信号实现结构损伤识别和定位的实时处理.Sharma 和 Sen (2020) 也利用一维卷积神经网络来定位半刚性框架中的损伤节点,使损伤检测的实时性明显提高.Yang 等 (2020b) 建立了一个同时对空间关系和时间关系建模的层次深度卷积神经网络与GRU 框架来进行损伤检测,CNN 被用来建立传感器之间的空间关系及短期时间依赖关系,且其输出特征被作为GRU 的输入以学习长期时间依赖关系.

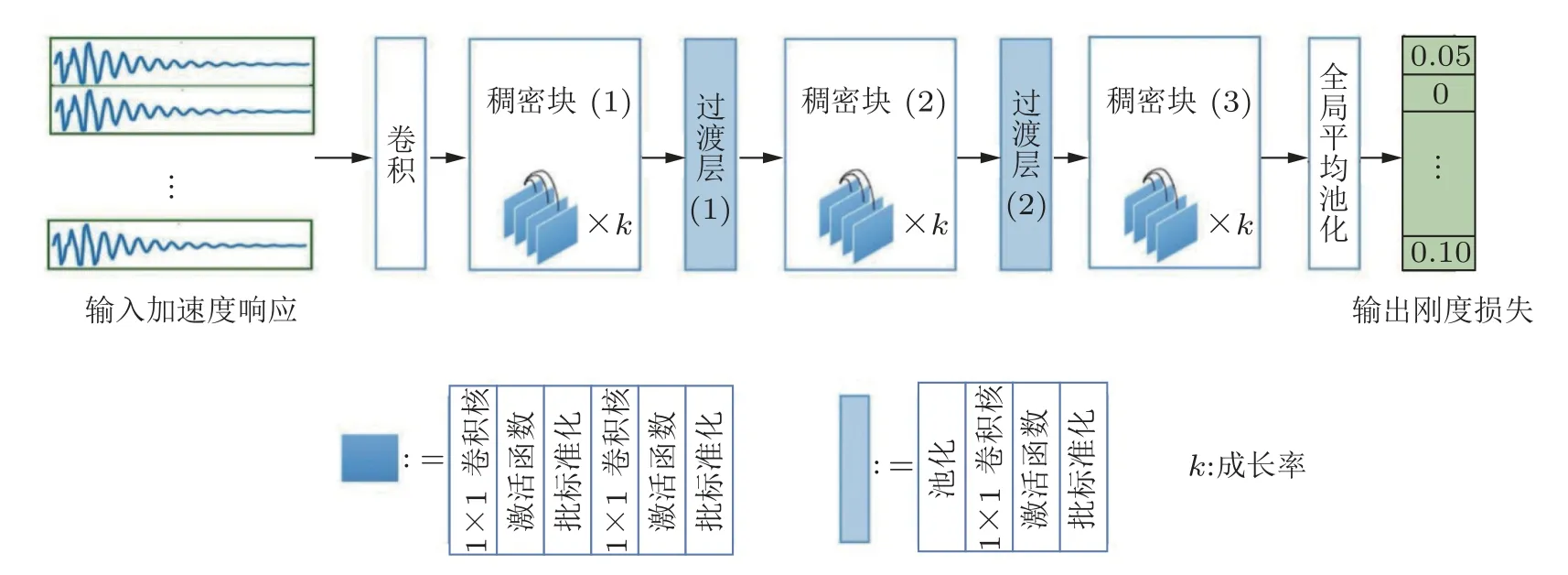
图7 结构损伤识别稠密卷积网络 (Wang et al.2021b)

虽然上述方法可以成功地识别结构损伤,但是这些研究的应用往往在较为理想的情况,未考虑实际应用不可避免的建模不确定性;此外,测试数据相对于待识别的损伤参数往往存在空间不完备性,且容易被噪声污染.这种情况下,网络参数的学习很难准确实现,严重影响损伤识别的效果.Ding 等 (2020) 提出了一种基于稀疏深度置信网络的结构损伤识别方法,结构固有频率和振型振动特征被提取作为深度置信网络的输入,结构的损伤位置和严重程度作为输出.引入稀疏约束有效提升了在空间不完备模态数据和模型不确定性下的网络性能.

此外,在相同外部载荷作用下,结构静态响应之间的相关性仅为结构参数的函数,并且与外部载荷无关,因此该相关性可以作为结构状态评估的指标.Xu 等 (2023) 提出了一种基于主梁挠度和索力之间时空概率分布相关性建模的斜拉桥状态评估方法(图8).相关性由无监督深度学习网络建模,该网络包括两个变分自动编码器 (AE) 和两个生成对抗性网络 (GANs).实际监测数据分析表明建立的索力的预测和真实的概率密度分布之间的Wasserstein 距离指标对损伤很敏感,当斜拉索发生损坏时会出现明显变化.

图8 结构损伤识别稠密卷积网络.(a) 主梁位移群和拉索索力群的时空概率分布相关深度学习模型,(b) 基于索力真实和预测分布Wasserstein 距离的斜拉索损伤识别 (Xu et al.2023)

相对于传统方法,基于深度神经网络的结构损伤识别方法能自动从数据中提取损伤特征,而无需特定的结构损伤指标的选取,避免了过多人为干扰的影响;同时,深度神经网络对于结构健康监测数据的实际噪声和环境干扰具有较强的鲁棒性.

4 基于监测数据的结构可靠性评估机器学习方法

在获取结构损伤状态信息的基础上,需要进一步对结构的服役可靠性进行评估,保证结构的服役安全.基于监测数据的结构可靠性评估包括荷载与环境及效应的建模、结构模型修正、可靠度计算等.对于基于监测数据的荷载、环境与效应等的统计分析与建模,以及结构模型修正方面的研究发展相对更早,并形成了诸多相对成熟的成果 (李惠等 2015).如何进行高效高精度的可靠度计算,仍是基于监测数据的结构可靠性评估亟须解决的关键问题之一.在过去的十年,机器学习技术得到了迅猛发展,促使传统土木工程步入人工智能时代 (鲍跃全和李惠 2019).在结构可靠度计算方法方面,国内外学者也开展了大量基于机器学习的结构可靠度计算方法研究,取得了一定的进展.

4.1 基于机器学习方法的结构系统失效模式搜索与识别

对于由数量巨大的构件组成且结构形式复杂的实际工程结构系统,其失效事件可由多种不同的失效模式引起,各个失效模式由多个不同失效构件按不同的失效顺序组成.因此,结构系统的失效概率可按下列公式计算

式中,Pf(t) 为结构系统的失效概率,P(FMi|t) 为失效模式i的概率,N结构系统的失效模式数量,Pf(ck|c1,c2,···,ck-1) 为构件ck在c1,c2,···,ck-1失效的条件下的失效概率.

在实际结构系统可靠度分析中,结构系统的失效模式数量巨大,在搜索过程中常常会遇到组合爆炸问题,难以根据以上公式对结构系统的所有失效模式进行失效概率计算.因此,根据结构受力状态,对结构系统的失效模式进行搜索与识别,并根据识别得到的主要失效模式对结构进行失效概率计算,是结构系统可靠度分析的常用手段.为应对主要失效模式搜索过程中的组合爆炸问题,Guan 等 (2022) 将基于失效概率的失效构件选择过程转化为序贯决策过程,提出了基于深度强化学习的主要失效模式搜索方法,应用于搜索过程中的失效构件选择,并通过算例验证了准确性与效率.随后,Guan 等 (2023) 将“自博弈”训练策略应用到该方法中,使深度强化学习的训练逻辑更切合主要失效模式搜索过程 (如图9 所示),在保证了计算精度的前提下,极大提高了深度神经网络的训练效率,降低了有限元计算成本.Huang 和Burton (2019) 提出了一种数据驱动的方法,通过采用机器学习方法来对填充框架的面内失效模式进行分类.并通过由114 个填充框架试件组成的实验数据库,对6 种机器学习方法进行了验证.为识别剪力墙的破坏模式,Mangalathu 等 (2020) 评估了8 种机器学习模型,并建立了一个包含393 个不同几何构型剪力墙的实验结果的综合数据库,提出了一种基于随机森林方法的机器学习模型.研究表明,纵横比、边界单元配筋指数和墙长与墙厚比是影响剪力墙破坏模式的关键参数.

图9 基于自博弈策略和深度强化学习的结构系统主要失效模式搜索方法.(a)方法流程,(b)桁架结构主要失效模式搜索结果

4.2 基于机器学习的结构可靠度计算方法

识别结构损伤后,可进一步更新结构有限元模型.通过监测数据建立的荷载、环境与效应概率模型,考虑结构抗力衰减与性能退化,可进一步采用可靠度分析方法评估结构的可靠性.结构可靠度是结构可靠性的一种度量,结构可靠度计算旨在确定结构发生失效的概率

式中,x是结构的随机变量,f(x) 是随机向量的联合概率密度函数,g(x) 是结构的极限状态函数.然而,对于许多实际工程结构,很难通过求解上述高维积分进行可靠度计算.模拟方法和代理模型方法是两种重要的结构可靠度计算方法.

随机模拟方法也称蒙特卡洛模拟,是一种最常见的结构可靠度数值模拟算法.蒙特卡洛模拟方法通过对结构进行随机抽样和极限状态函数模拟计算,根据失效样本比例估计结构失效概率.然而,传统模拟方法需要大量的模拟样本才能准确估计结构失效概率,在大型工程结构可靠度分析中的计算量难以接受.重要抽样和子集模拟等方差缩减技术是减少结构可靠度计算模拟方法中随机样本数、提高可靠度计算效率的主要手段.但传统的方差缩进技术在实际工程应用中仍存在许多不足,主要表现为对目标抽样密度的抽样效率较低.为此,Yin 和Kareem (2016) 提出了基于分层聚类的结构可靠度分析方法,采用无监督学习方式进行样本的聚类分析,有效降低结构可靠度数值模拟方法的计算量.Luo 等 (2022) 等提出了一种基于主动人工神经网络与传统蒙特卡洛采样结合的方法,实现了结构失效概率的高效近似.Xiang 等 (2023) 提出了基于可解释深度生成网络的结构可靠度重要抽样方法,利用深度生成网络可解释性实现结构重要抽样密度函数抽样,提高可靠度计算效率和精度 (如图10 所示).

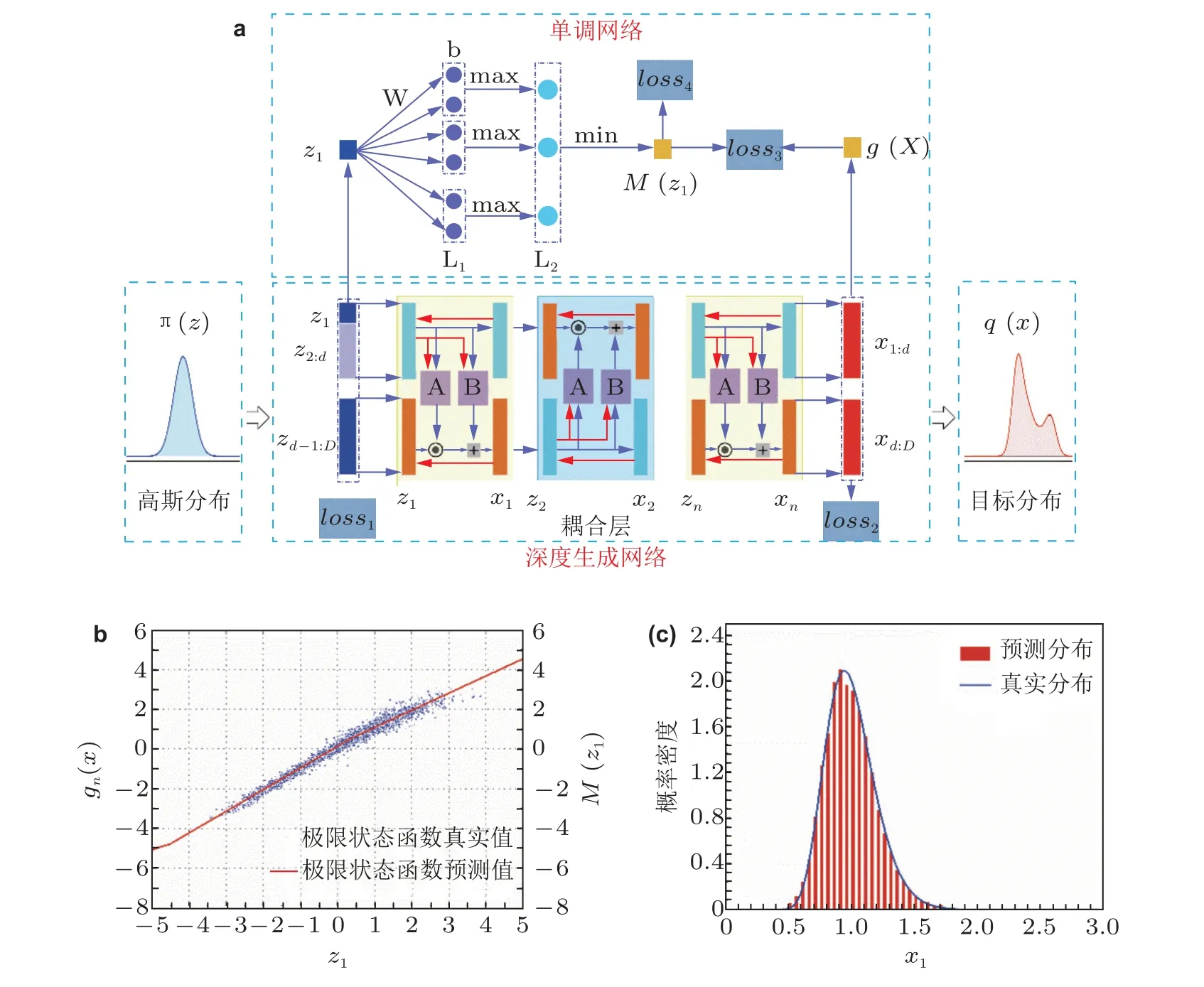
图10 基于可解释深度生成网络的结构可靠度重要抽样.(a)可解释深度生成网络重要抽样模型,(b)输出样本极限状态函数值,(c)输出样本概率分布 (Xiang et al.2023)

代理模型方法通常采用一个容易计算的近似模型替换结构真实模型,从而降低结构可靠度计算代价.然而,代理模型在进行可靠度分析之前需要足够的训练样本以保证模型的预测精度,传统代理模型在高维强非线性极限状态函数问题中训练样本选择效率较低、模型预测精度不足.随机变量的降维和代理模型的主动学习是解决上述传统代理模型问题的主要途径.Li 和Wang (2020) 提出了高维可靠度分析的深度学习方法,利用自编器的特征抽取能力,实现高维可靠度问题的降维.Wang 等 (2021a) 提出了基于自适应贝叶斯支持向量回归的高效结构可靠性分析方法,提出了新的学习函数以提高支持向量回归模型的主动学习效率.Xiang 等 (2020a) 提出了基于深度强化学习的结构可靠度分析抽样方法,进而建立高效的深度神经网络代理模型,提高强非线性极限状态函数问题的可靠度计算精度和效率 (如图11 所示).Lieu 等 (2022) 开发了一种基于深度神经网络的自适应代理模型,通过全局与局部预测,有效地提高了极限状态函数的计算效率和准确度.为了解决传统主动学习方法中训练样本选择的局部最优问题,Bao 等 (2021)和Xiang 等 (2020b) 提出了基于权重抽样和自适应子集搜索的结构可靠度计算深度神经网络方法,给出了用于不确定性样本选择的自适应子集搜索策略,同时建立了基于概率密度的权重系数以保证训练样本的均匀性.

此外,也有学者尝试将改进抽样和代理模型等方法与其他可靠度计算方法相结合,提升可靠度计算方法的性能.Ren 等 (2022) 提出了集合克里金和人工神经网络的可靠度分析方法,建立了局部最优代理模型和局部权重平均代理模型两种模型集合策略,有效提高了代理模型的预测精度.Zhou 和Peng (2022) 提出了基于深度学习和概率密度演化的可靠度分析方法,利用深度学习实现随机变量降维,采用概率密度演化确定样本的极限状态函数值,进而建立高斯过程回归模型.Cui 和Ghosn (2019) 提出了基于机器学习的结构可靠度计算子集模拟方法,将克里金模型和聚类算法与传统子集模拟方法融合,提高子集模拟计算效率.

相比传统方法,深度强化学习等机器学习方法具有较强的自学习和序贯决策能力,可以有效解决结构系统失效模式搜索与识别中的组合爆炸问题,实现复杂系统主要失效模式的准确识别;通过挖掘深度神经网络和深度生成网络等机器学习模型的高维非线性函数近似和表达能力,能够高效建立结构极限状态函数和响应概率密度函数等高维预测模型,实现结构可靠度高精度计算.