公共交通对健康城市医疗服务公平性影响研究

温旭丽，张志成

(东南大学成贤学院 土木与交通工程学院，江苏 南京 210088)

从既有文献看，国内外学者已经开展了公共交通公平性相关研究。LITMAN[1]指出交通决策往往对公平性具有重要影响，通过定义不同类型的交通公平，讨论了各种公平问题。THOMOPOULOS等[2]提出了一种基于MCA层次分析法将公平问题纳入交通基础设施项目评估的方法。DELBOSC等[3]认为公平性一直是公共交通服务的主要问题之一，提出了一种利用洛伦兹曲线来测量人口相对公共交通供给的新方法。WELCH等[4]提出一种基于综合路线、时间表、社会经济、人口和空间活动模式等因素的图论方法，以衡量公共交通服务公平性。GRIFFIN等[5]提出了一种基于收入的交通公平性分析方法。JEDDI YEGANEH等[6]认为获得高质量的公共交通对就业至关重要，利用回归分析方法探讨了按种族和收入划分的公共交通就业机会趋势。国内学者结合我国公共交通发展情况也开展了丰富研究。唐子来等[7]基于社会公平理念提出了用于轨道交通社会公平绩效评价方法。刘明辉[8]基于构建的公共交通供给指数综合评价指标，以武汉为例分析了公共交通设施空间分布公平性。潘亚伟[9]提出了我国健康城市的横向和纵向“多模式”公共交通体系结构模型。戢晓峰等[10]基于底线公平理论，采用主成分分析方法对城市公交的底线公平性进行了分析。戢晓峰等[11]设计了公交出行调查问卷，并运用结构方程模型分析了昆明公共交通系统公平性。王欢明等[12]对大连市公共交通服务公平性和影响因素进行了分析。杨庭[13]通过对比公共交通和小汽车交通的出行成本和可达性差异，评价分析了广州市交通出行公平性。侯松岩等[14]基于ArcGIS和网络分析法，以最短可达时间和公交服务频次为分析指标，研究了长春市医院可达性的时空分布特征。既有成果主要从公共交通作为城市公共服务资源的公平性角度来展开相关研究，尚未涉及针对公共交通对城市公共服务公平性影响的研究。对于健康城市来说，公平性是一个比贫困更广泛的概念。贫困主要是针对某个贫困线以下的人口，而公平性对整个人口范围而言。经济学中，通常运用基尼系数、泰尔系数和变异系数等指标来量化城市收入公平性，公平性衡量标准通常是根据支出以外的分配来计算，这些指标主要考虑人均收入的影响。而公共交通对健康城市服务公平性影响也可以选用人均收入指标来考量，因此本文将这种公平性概念引入城市公共交通对健康城市服务公平性影响研究当中，以此开展研究。

1 指标选取和数据来源

1.1 健康城市公共服务指标

根据《全国健康城市评价指标体系(2018版)》中提出的城市健康评价指标来设置和选取健康城市公共服务指标，结合数据可得性、可比性和科学性等原则，选用城市每万人口拥有公共卫生人员数作为健康城市公共医疗资源水平代理指标。

1.2 解释变量指标

从2个角度来设计和选取公共交通系统的解释变量指标。一是面向健康城市公共交通服务供给方面；二是面向公共交通服务需求方面。数据来源于2种方式，一种是居民出行调查统计数据，另一种是城市年鉴统计数据。指标选取见表1。

表1 公共交通面向健康城市服务公平性指标Table 1 Public transportation face to the fairness of urban medical public service indicators

以南京市公共交通和城市医疗公共服务为研究对象。根据中国社会科学院发布的《城市蓝皮书：中国城市发展报告No.11》，南京城市健康发展指数综合排名居全国第9位，江苏省第1位，故以南京作为健康城市样本具有较好的代表性。公共交通分担率指标的统计数据来源于《南京市交通年报(2001～2017)》，所涉及的城市医疗技术人员的样本数据来源于《南京统计年鉴(2001～2017)》，其中人均GDP数值统一换算成2000年可比价，以消除价格因素影响，满足不同历史数据对比需要。样本数据属于时间序列数据集，数据描述统计情况如表2所示。为消除异方差影响，同时便于拟合系数比较和结果分析，对样本原始数据采用Z-Score标准化方法进行标准化和无量纲化处理。计算公式为其中，x＇表示标准化之后的数据；x表示原始数据；xmean为样本均值；d为原始数据标准差。

表2 样本数据描述统计Table 2 Descriptive statistics of sample data

2 加权基尼系数取值和模型选择

2.1 加权基尼系数

基尼系数是研究经济分布不平等程度(公平性)的一个重要指标，用来衡量一个国家的财富或收入分配与完全平等的分配差距有多大，可以通过Lorenz曲线来实现。对于Lorenz曲线未知情况，可以采用公式(1)来计算加权基尼系数：

式中：ni=Ni/N表示第i个区域的人口权重；yi表示第i个区域的平均收入；yˉ(w)表示加权平均收入。

本文借鉴加权基尼系数指标公式来构造适合健康城市公共服务公平性评价的方法，分为2类，即按照人口和GDP为权重的加权基尼系数，通过替换公式(1)中对应参数从而计算得出2种形式的加权基尼系数具体数值。

2.2 普通线性回归分析(OLS模型)

该模型的表达式一般可以写成：

式 中：响 应 变 量Y=(y1，y2，…，yn)T；自 变 量X=(X(1)，X(2)，…，X(d))，对 于 每 一 个X(j)，有X(j)=假 设 每 个1，2，…，d)均已标准化，随机误差项εi～N(0，σ2)，(i=1,2,…,n)，ε=(ε1，ε2，…，εn)T， 回 归 系 数β=(β1，β2，…，βd)T。当X为列满秩设计矩阵时，回归系数β可由普通最小二乘估计(OLS)方法求得：

当设计矩阵X不满足列满秩时，将不能采用普通最小二乘法来求解回归系数β，此时引入惩罚方法，可同时满足变量选择和参数估计要求。在参数估计时，通过将部分参数压缩为0以达到变量选择的目的。

在多元回归中，被解释变量常受到很多因素共同影响，如何根据研究目标选择合适的被解释变量进入回归模型是首先需要考虑的问题。如果引入的解释变量较少，回归模型将不能对被解释变量变化规律做出较好解释，但解释变量个数也并非越多越好，由此可能引起变量间多重共线性问题，造成参数估计结果非有效和方差增大等问题。本文采用逐步筛选策略(Stepwise strategy)对回归模型的解释变量进行筛选。计算结果如表3所示。从表中可以看出，利用逐步筛选策略将公交客运量，人均GDP，公交标台车数以及城市道路里程等变量剔除在回归模型之外。影响最大的是绿色出行分担率，其系数为正，说明提高绿色出行分担率不利于医疗资源的公平性。在负向指标中，影响最大的公交指标为公交车公里分担率，为-4.310 6，即提升该指标有助于提升公共服务公平性。

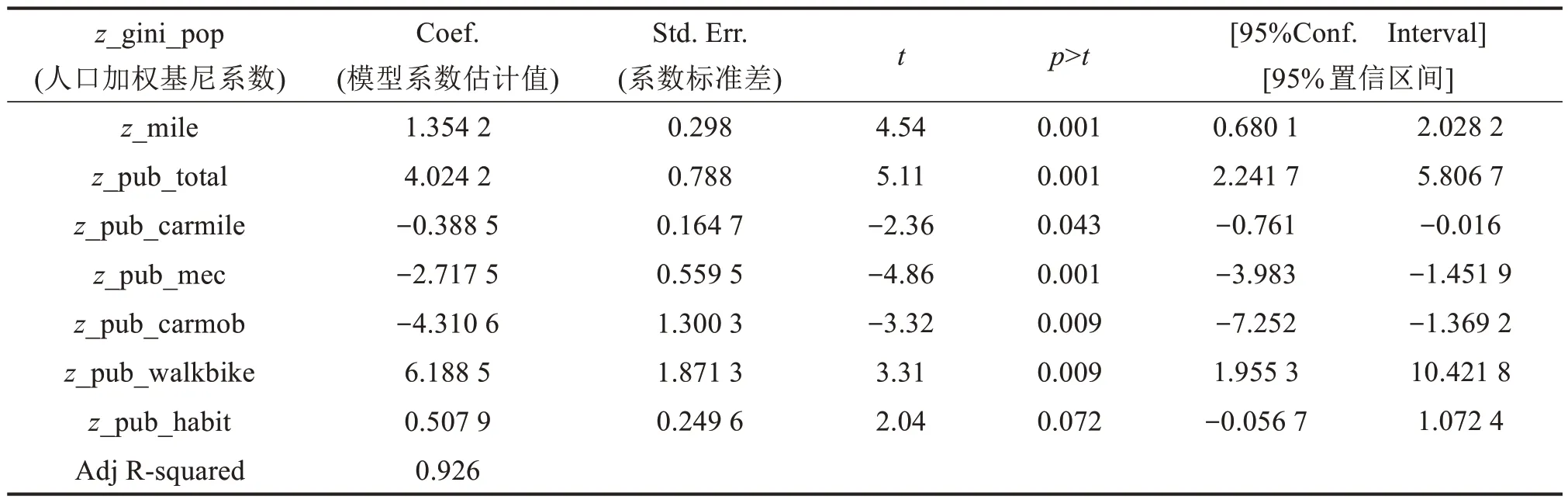
表3 最小二乘回归分析结果Table 3 Results of OLS regression analysis

以上回归结果的可靠性还需要从变量共线性、残差独立性和异方差等方面进行回归后检验分析。

1) 变量共线性检验。采用方差膨胀因子(VIF)来判断自变量间是否存在共线性问题。一般情况下，VIF值不大于10则说明变量间不存在共线性问题[15]。由表4可知，VIF的变量最小值为5.863，平均达到194.715，存在严重的共线性问题。

表4 变量膨胀因子Table 4 Variance inflation factor of variables

2) 异方差检验。分析结果见表5。根据怀特检验结果(p=0.385 6大于0.05显著水平)，说明样本数据异方差现象并不明显。

表5 怀特检验结果Table 5 White test results

2.3 岭回归分析(Ridge Regression)

Ridge方法中对于β的估计公式为：

也可以写成：

参数含义同LASSO回归模型，γ由λ或t决定。可以看出岭回归方法估计的是β的有偏估计，即且岭回归估计结果是将OLS估计以相同比例进行了压缩。岭回归和LASSO回归方法最大的区别在于后者采用的是L1penalty，岭回归是L2penalty。以二维数据空间为例，图1中左图对应于LASSO方法，右图对应于Ridge方法。

图1中，椭圆代表随着λ变化的残差平方和函数等高线，̂是椭圆中心点，对线性模型最优解。左右2个图的区别在于约束域分别对应图中原点区域。对于LASSO方法，将不显著的变量系数压缩至0以达到变量选择的目的。Ridge方法虽然也对原本的系数进行了一定程度的压缩，但是任一系数都不会压缩至0，最终模型保留了所有的变量。

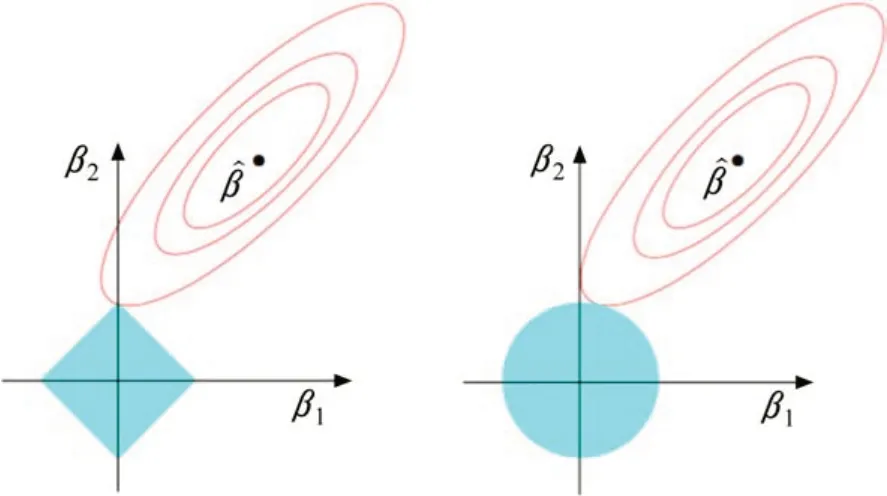
图1 LASSO(左)和岭回归(右)差异对比Fig. 1 Difference between LASSO (left) and Ridge Regression (right)

图2是岭回归模型求解路径，最优λ值为19.64。模型求解得出的各变量回归系数如表6所示。结合图2和表6可知，对加权基尼系数具有正向边际效应的变量指标包括人均GDP，城市道路里程，公交运营线路网长度，公交全方式分担率以及公交车车标台数，其余指标为负向指标，影响最大的2个指标为公共交通车公里分担率和公共交通机动化出行分担率，指标的提升可以促进健康城市医疗资源公平性。总体上，边际效应较小的2个公交指标为公交全方式分担率指标(0.004 7)和公共交通客运总量(-0.025 2)。

图2 Ridge回归模型求解路径(λopt=19.64)Fig. 2 Solution path of Ridge regression (λopt=19.64)

从表6中的Ridge回归系数一列中也可以看出，与岭回归相比，OLS回归方法对各解释变量的拟合估计值都变大。

2.4 LASSO回归分析

LASSO方法是在普通线性模型中增加L1惩罚项，对于普通线性模型的LASSO估计为：

式中：t与λ相对应，是一个决定规则化程度的预定的自由参数，为调节系数。令当t

图3给出了LASSO回归模型求解路径，最优λ值为2.48。该模型求解得出的各变量回归系数如表6中的LASSO拟合系数列所示。结合图3和表6可知，在最优调整系数下，仅有公交车公里分担率指标、公交机动化分担率指标以及城市道路里程3个指标进入最终回归模型。对加权基尼系数具有正向边际效应的为城市道路里程指标，其余2个指标为负向效应指标，进一步说明提升公共交通车公里分担率指标和公共交通机动化出行分担率指标将促进健康城市医疗资源公平性。但LASSO回归系数比Ridge回归系数略大一些，但仍然比OLS回归系数小(见表6)。

表6 3种回归分析结果汇总表Table 6 Regression results of the three models

图3 LASSO模型求解路径(λopt=2.48)Fig. 3 Solution path of LASSO regression (λopt=2.48)

2.5 弹性网回归分析(Elastic net)

弹性网回归分析是一种同时使用L1penalty和L2penalty为先验正则项的线性回归模型。它的计算公式为[16]：

易知，当α=1或者令α=0时，弹性网络模型可以分别简化成LASSO模型和Ridge模型，也就是说，后两者是弹性网络模型的特例。图4列出了3种模型拟合函数之间的差异性。

图4 LASSO，Ridge和Elastic Net回归拟合损失函数变化差异Fig. 4 Difference among the three regression models

图5为弹性网回归模型的求解路径分析。模型调整系数λ的最优值为4.96，与LASSO回归分析结果相同，仅有公交车公里分担率指标、公交机动化分担率指标以及城市道路里程3个指标进入最终回归模型。相比Ridge回归和LASSO回归模型，这3个公共交通指标同样保持了相同的变化方向，进一步验证了这3个指标对于城市医疗服务加权系数边际效应的一致性。从回归系数大小来看，与LASSO模型差别不大。

图5 弹性网模型求解路径(λopt=4.96)Fig. 5 Solution path of elastic net(λopt=4.96)

3 模型应用

综上，选择弹性网回归模型，由表7得出南京城市医疗公共服务水平加权基尼系数与公交分担率回归方程为：

表7 模型选择准则指标值Table 7 Model selection criteria index values

从回归模型可以分析得出：

1) 南京城市医疗公共服务加权基尼系数主要受到公交车公里分担率、公交车机动化分担率和城市道路里程3个指标影响。

2) 对城市医疗公共服务基尼系数产生负向边际效应最大的是公交车机动化分担率指标，其次为公交车公里分担率，故增加这2个指标有助于提升南京城市医疗公共服务公平性，这与目前大多数公交都市建设目标一致。

4 结论

1) 分析研究了基尼系数及加权基尼系数研究经济分布公平性方面的应用及计算方法，结果表明，将衡量城市收入公平性的量化指标基尼系数引入城市公共交通评价是合适的。

2) 设计提出了城市医疗公共服务的加权基尼系数公平性评价方法，梳理了岭回归、LASSO回归和弹性网回归方法以及相应的模型选择方法，在此基础上构建了公交分担率指标与城市医疗公共服务加权基尼系数的多元回归计量模型。结果表明，弹性网回归模型能够较好地描述公共交通担率指标对城市公共服务公平性影响关系。

3) 运用所构建模型对南京市医疗服务公平性进行分析评价。结果表明，影响南京城市医疗公共服务公平性的正向指标为公交车公里分担率、公交车机动化分担率和城市道路里程，增加这3个指标有助于提升南京城市医疗公共服务公平性。研究成果有助于为健康城市社会公平性建设目标实现提供理论基础和政策依据。

本文分析了公共交通分担率指标与城市医疗公共服务公平性之间的相关性和数量变化规律，重点考察了基于公交分担率的公共交通与医疗公共服务影响评价的方法构建和验证，研究方法可以用于除了医疗公共服务以外的教育资源、体育活动场地和公园绿地等服务公平性研究。需要指出的是，文中所讨论的公平性是指健康城市的医疗服务资源的公平性，不是公共交通本身的公平性。今后将进一步开展更具普遍性的研究，类推其他不同规模和不同层级的城市公平性问题。