高速铁路接触网系统维修决策优化

2023-02-24池瑞邱国龙曾庆森屈志坚池学鑫

铁道科学与工程学报 2023年1期

池瑞，邱国龙，曾庆森，屈志坚，池学鑫

(华东交通大学电气与自动化工程学院，江西南昌 330013)

铁路牵引接触网系统在铁路系统中占有极其重要的地位，其主要作用是把从牵引变电所获得的电能传输给在铁路上运行的机车，如果接触网系统发生故障将会使铁路运输中断产生巨大的损失。因此，针对接触网系统制定合理有效的维修策略对于电气化铁路安全高效地运行具有十分重要的意义[1]。随着铁路系统的高速发展，国内外已有许多关于接触网系统维修优化的研究成果。有学者就接触网系统的维修优化模型进行改进，陈绍宽等[2]考虑以可靠性为约束建立接触网最小维修优化模型通过案例研究证实了其正确性与可靠性。赵亚辰等[3]将更新收益定理和时间延迟理论运用在优化模型中以维修费用最低为优化目标求解得到了较为理想的结果。程志君等[4]运用机会维修思想建立了复杂条件下的视情维修决策模型，算例分析结果表示该模型具有较好的实用性。苏春等[5]以隐半马尔科夫模型进行动态建模以维修费用率最小化为目标来求解，为维修计划制定提供了理论基础。张友鹏等[6]采取基于嵌套粒子群结构的维修决策优化方法进行多目标的优化，通过验算证实了该方法可有效提高系统可靠度和可用度、降低维修成本。PANG等[7]采用改变模型目标值来提升解的可行性。何勇等[8]提出分阶段预防性维护优化模型，用案例表明了多目标优化的优越性。但总的来说，目前绝大多数的研究都是基于可靠性来建立维修优化模型。也有学者对接触网系统维修优化模型的算法进行改进，李雪等[9]建立了接触网系统可靠度和维修费用模型，提出一种改进的混沌自适应进化算法来对接触网维修策略进行优化，该算法的优点在于改进了NSGA2算法的初始种群、选择策略和遗传算子3个关键算子，增强了算法的局部和全局搜索能力。通过分析验证了多目标寻优的优越性。陈民武等[10]基于GO法对系统进行可靠性的评估，采用离散粒子群算法设计了维修优化策略，通过仿真分析证实了模型的实用性和可操作性。李耀华等[11]利用自适应变异粒子群算法对目标进行求最优解，通过模型验证分析表明该算法所得最优解能有效降低成本。刘琛等[1]在考虑接触网与供电设备的基础上，通过构建Petri网来进行分析计算。建立了风险相关的模型来对接触网系统因故障而导致的损失进行评估，并且将其与维修成本作为约束来制定维修成本最小的维修策略。在优化模型中还加入了役龄回退因子，运用混合PSO算法来得到能使系统安全可靠运行的优化方案。史振伟[12]提出以贝叶斯网络来进行策略优化在降低维修费用，提高维修效率等方面具有明显的优势。SUN等[13]提出了与混合插值算法结合的方法提升了解的精度。LI等[14]采用在算法中加入模糊综合评价法从非劣解中得到最佳解。GU等[15]引入差分进化算法的变异和交叉来代替遗传算法以提高解的收敛性。ZHANG等[16]通过在算法中加入γ向量使计算优化参数更加精确。目前关于维修优化模型的算法的研究主流是在NSGA2算法的基础上加以改进[17]。本文提出的多目标布谷鸟遗传算法主要是基于李雪和陈绍宽的研究上，创新性地提出了一种多目标布谷鸟-遗传算法。在算法中采用Tent混沌映射生成多样性较好的初始种群；同时加入布谷鸟搜索算法中的levy-flights算子，提高局部和全局搜索能力；引入优化选择因子Pr动态调整优化机制。综上所述，本文建立以系统可靠性为约束条件，维修成本最低为目标的维修优化模型，提出了改进后的多目标遗传算法寻找最优方案进行优化。

1 接触网系统的可靠性与费用模型

电气化铁路接触网系统由多个部件组成，如果对所有的组成部件都进行建模分析工作量太大，可行性不高。通过分析接触网系统相关的研究资料，可以对其中7个主要的组成部件进行建模分析。在综合考虑之后，以威布尔函数来对主要部件的可靠性进行建模，而由于其他部件对整个系统的影响相对较小，因此采用指数分布来表达其可靠性。

本文对考虑维护成本与系统可靠性的2个函数的优化问题进行研究，属于周期性的检修。主要部件的可靠性用威布尔函数[18]表示为：

其中：t表示时间；R0表示设备的初始可靠度；α和β分别表示威布尔函数中的尺度参数、形状参数。

除了这7个主要的部件，其余部件正常运行的概率用指数函数表示。指数分布[18]表示的可靠度函数为：

其中，γ表示指数函数的参数，γ>0，t>0。

接触网系统的主要部件的维护方式可以分为完全更换、大修、小修和不修4类。其中完全更换是指当前设备在进行了多次维修后依旧无法符合要求或者继续维修的成本要高于完全更换的成本时，在这些情况下就要对设备或局部子系统进行完全更换。完全更换能够较好地提高整个系统的可靠性，但缺点是维修费用相对较高。大修是指对设备进行机械性维修，改善设备的外部工作环境，同时对一些结构简单的部件进行及时地更新替换，比如对吊弦、定位器等较简单的部件加以调整与更换。小修是大修的一部分，仅指简单的机械性维修，外加改善设备的外部工作环境，例如对设备进行去锈、除污、润滑等简单的机械性维护。不修是指当前设备可靠度满足运行要求，可以使系统安全可靠地运行，那么该设备可以不维修而继续使用。在考虑经济性的前提下应以小修与大修来作为维持其能可靠运行的主要改善方式。对于一些运行后损耗较小的部件，其发生故障的概率较小且能够在较长时间下保持较高的可靠性，因此采取完全更换的维修方式概率更小，维修费用也较低。而一些部件由于其工作时损耗较大或者工作环境比较恶劣，那么其可靠性也较低，需要采取大修或完全更换的维修方式，因而维修费用较高。基于以上所述在综合考虑各个部分的维修费用与正常运行的概率之后来制定周期性维修计划是十分合理的。在建立的检修计划模型中，t，NP和tp等都是已知的常数来考虑的。各部件在第k次检修阶段能正常运行的概率函数如下：

其中，R0，k是相应设备在k个维修阶段的起始可靠度；m1是采用小修维修方式时对系统的改善因子。如果在k个阶段的起始采用小修的维修方式，则式(3)的R0，k可表示为：

其中，R0，k-1是第k-1次检修周期开始正常运行的概率，Rf，k-1是第k-1次检修周期最终能够正常运行的概率。如果在第k个阶段的起始采用大修的维修方式，则式(3)的R0，k可表示为：

其中，m2是大修维修方式时对系统的改善因子，R0是新元件的起始可靠度。如果第k个周期的起始采用完全更换的维修方式，则式(3)的R0，k可表示为：

接触网能够正常运行的概率应为各个部件能正常运行的概率的乘积。在建模中的7个主要部件是相互独立的，其与接触网系统的其它部分也是看作相互独立的。每个维护周期选择的检修方式是不同的，因而整个接触网系统的能正常运行的概率也随之发生改变，其能正常运行的概率可用式(7)表示：

其中，Rc(t)表示其他部件能正常运行的概率；σn表示当第n个部件不能正常运行使得整体不能正常运行的概率。系统能正常运行的平均概率可用式（8）求得：

总的维护成本函数如下：

其中，j代表维修方式，j=1, 2, 3, 4分别代表不修、小修、大修、完全更换；Cn，j代表研究的7个主要部件中第n个部件采取第j中检修方法的费用；pn，k，j代表第n个部件在第k次检修中是否采取第j种检修方式，其值为0或1；Cn，h代表第n个部件非正常运行时的抢修费用，hn，k(t)代表第n个部件在第k次检修的周期里不能正常运行的概率，NP代表检修次数。hn，k(t)可表示如下：

其中，Rn，k(t)代表第n个部件在第k次维护周期里能正常运行的概率。

综上所述，式(8)为接触网系统的可靠性模型，式(9)为接触网系统的维修费用模型。以这2个函数作为多目标优化的主函数，通过改进后的优化算法来对其进行优化，来得到一个可靠度较高且维修费用较低的维修策略。

2 布谷鸟搜索遗传算法

2.1 NSGA2算法

NSGA2算法是目前解决多目标优化问题中较为优秀的算法之一。NSGA2算法中引入了锦标赛选择算法和精英策略，同时采用快速非支配排序方法，并结合拥挤度比较算子来得到最优解。但NSGA2算法也存在收敛速度慢和解均匀分布性较差的问题。NSGA2算法的主要框架为，父代进行交叉、变异等操作形成子代，随后经过快速非支配排序和拥挤距离排序从父代和子代中选择优秀的个体保留，直到满足条件输出优化结果。

2.2 布谷鸟搜索遗传算法

NSGA2算法的全局优化性能较好，但是其局部优化性能差[19]。然而布谷鸟算法全局寻优效果与局部寻优效果都较好，由于其局部寻优是围绕最优解附近的，因此其局部寻优效果突出[20]。将NSGA2与CS混合可以得到一个更好的优化效果。布谷鸟搜索遗传算法就是将NSGA2与CS这2种算法进行结合，该算法可以有效改善局部搜索效果，同时增强它的全局范围的优化效果。

2.2.1 Tent混沌映射算法

在算法中加入Tent算法增加个体的多样性，使其优化效果更好。参考刘园园等[21-22]的研究，融合了Tent映射算法产生的序列更优，对于整个算法的优化效果更好。其数学模型如式（11）所示：

式中：xn是随机生成的小数。

2.2.2 布谷鸟搜索算子

在算法中加入了levy-flights算法，其作用是产生新的可以放置鸟蛋的位置，有效地改善了局部搜索效果，也改善了全局范围的优化效果。如式(12)～(14)所示：

2.2.3 优化选择因子Pr

在算法中加入了优化选择因子Pr[23-26]，更好地分配NSGA2的全局性寻优机制与CS的局部性优化机制。合理地分配选择全局寻优与局部寻优能使算法得到一个更好的优化效果。

3 仿真结果与分析

3.1 维修模型相关参数

为了验证改进算法的优化效果，以文献[27]中郑州供电段的某一段线路的接触网相关部件的数据进行仿真分析。接触网的有效时间是168月，检修间隔tp是12个月，次数Np是13，种群大小N是120，其他相关参数如表1所示。

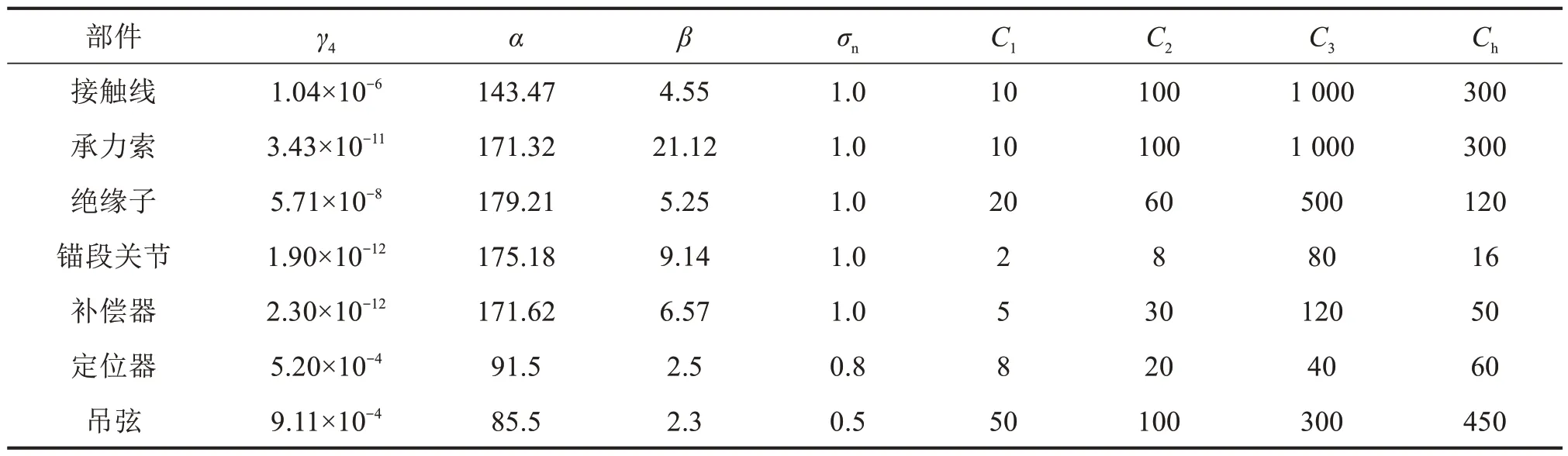
表1 各部件的相关参数和维修费用(维修费用/千元)Table 1 Related parameters and maintenance cost of each component (maintenance cost/thousand yuan)

其中，α为威布尔函数中的尺度参数，β为威布尔函数中的形状参数；σn为接触网系统中第n个设备发生故障致使整个系统发生故障的概率；C1表示小修所需维修费用，C2表示大修所需维修费用，C3表示完全更换所需维修费用，Ch表示事后抢修费用；m1=m2=0.8。

同时在验证中假设接触网各设备的转移概率符合公式[20]：γ1=0.8γ，γ2=0.8(γ-γ1)，γ3=0.8(γ-γ1-γ2)，γ4=γ-γ1-γ2-γ3，接触网系统其他部分的可靠度服从γc=10-6的指数函数分布。

3.2 初始种群比较

NSGA2算法由随机函数来生成初始种群，而CSGA算法采用的是Tent混沌映射算法来生成初始种群。图1(a)是NSGA2算法生成的初始种群的结果，图1(b)是CSGA算法生成的初始种群的结果，计算效果的比较如图1所示。

图1 初始种群的比较Fig. 1 Comparison of initial populations

通过比较中可以看出NSGA2算法生成的初始种群效果不如CSGA算法。图1(a)中的初始种群大部分都集中在一块，分布性远不如图1(b)中的好。而种群分布的均匀性直接与算法优化的效果相关，分布更加均匀的种群对算法的全局优化效果以及最终的寻优结果更加的有利。

3.3 不同改进下的优化效果

图2是在NSGA2算法中加入了不同的改进方式后迭代400次计算所得到的仿真结果。图2(a)是用NSGA2算法优化的仿真结果，图2(b)是在NSGA2算法中将初始种群生成方式改为Tent混沌映射算法时的仿真结果，图2(c)是基于图2(b)的基础之上加入了CS算法后的仿真结果，图2(d)又是在图2(c)基础上加入了优化选择因子Pr后的仿真结果。由图2所示的仿真结果可知，在NSGA2算法中通过Tent混沌映射算法来生成初始种群，同时加入CS算法和优化选择因子Pr后，算法的局部寻优性能与全局寻优性能都得到了有效的改善，该算法的优化性能相对于原始的算法有了很大的提升。

将图2(a)与图2(b)的进行对比可以看出把NSGA2生成初始种群的方式替换为Tent混沌映射时优化的最优解更好，即所得最优解可使接触网可靠性较高同时费用较低。图2(c)在加入CS算法后优化效果得到了进一步提升，同时最优解的数量更多。从图2(d)结果可以看出，在加入Pr选择因子后优化效果又有了更大的提升，其优质解多且集中。需要指出的是，在最优前端分布的解在理论上是最优的，在实际工程中选择怎样的维修方案主要取决于决策者的实际需要。与图2(c)相比图2(d)结果的可靠性已经达到了一个理想的水平，在满足高可靠性的要求下其维修费用进一步减少，所得优化效果明显更好。

3.4 采用CSGA算法的优化过程

图3为对比于NSGA2采用CSGA算法优化的过程图。其中Np=13。

图3(a)，3(c)，3(e)和3(g)是CSGA算法进行初次迭代、迭代100次、迭代200次、迭代400次的优化结果。图3(b)，3(d)，3(f)和3(h)是NSGA2算法进行初次迭代、迭代100次、迭代200次、迭代400次的优化结果。在图3的对比分析中可以看出优化次数越多，那么算法所得到的优化效果更好。同时经过对比分析可以看出CSGA算法的优化性能明显较NSGA2算法要好。其初代个体的分布性、最优解的品质更好。

图3 CSGA优化过程仿真结果Fig. 3 Simulation results of CSGA optimization process

3.5 维修次数Np为13的优化结果

CSGA算法用MATLAB编码来实现。实验是在Microsoft Windows10，Intel Core i7 8750@2.20 GHz和8GBRAM的配置下运行。设种群N=120，交叉概率pc=0.9，变异概率pm=0.1，模拟二进制交叉参数mu=20，多项式变异参数mum=20，迭代次数200代，优化过程时长为84.686 238 s，图4为维修次数Np为13时优化的仿真结果。

图4 优化结果Fig. 4 Optimization results

在图4中可以看出结果中有一部分优质解是品质较好的，在图4中左边部分的可靠度较低，而其右边部分可靠度相对左边增加不多但维修费用增加较快。在对应解品质较好的区间里，所对应是维修方案较好的优化结果，是可取的优化方案。在这里选取E点作为此次优化的结果，表2是对应E点的维修方案。

图5是在表2所述方案下几个维护量较大的部件与系统的可靠性动态分布图。

表2 维修点E方案Table 2 Maintenance plan E

图5 可靠度动态分布Fig. 5 Reliability dynamic distribution diagram

由图5可知，损耗较大的3个设备在维修方案下可靠度可达到0.97以上，且系统总体动态可靠度可达0.95以上，总的维修费用为371.2万元。如果假设接触网系统的可靠度达到0.95即满足运行安全性要求[2]，那么本次优化的结果很明显是符合要求的，达到了比较理想的效果。案例结果表明，吊弦和定位器在接触网中是损耗比较大的，需要进行的维修量因此较大，这与实际经验相符合。