横风作用下高铁全封闭矩形声屏障气动性能

2023-02-24黄永明何旭辉邓锷邹云峰

铁道科学与工程学报 2023年1期

黄永明，何旭辉，邓锷，邹云峰

(1. 中南大学土木工程学院，湖南长沙 410075；2. 中南大学高速铁路建造技术国家工程研究中心，湖南长沙 410075；3.香港理工大学国家轨道交通电气化与自动化工程技术研究中心香港分中心，香港 999077；4.香港理工大学土木与环境工程系，香港 999077)

目前，我国高速铁路建设已处于快速发展阶段，总里程已达3.5万km[1]，尤其在我国沿海地区已规划(有部分已建成)多条重要的高铁线路。随着高铁线路频繁穿越居民聚集区，由列车高速运行所引起的噪声污染问题也逐渐凸显[2]，多种型式的声屏障在该区域的高铁沿线得到大量推广运用。由于受东风气流、季风槽和西太平洋副热带高压的影响，在西太平洋上生成的台风有相当大一部分会移向我国，主要在我国东南沿海地区登陆[3]，从而导致该地区高铁桥上声屏障结构频繁遭遇强横风侵袭。高铁沿线上常用的声屏障型式有直立板式、半封闭式、全封闭整体弧形式以及全封闭矩形式等[4-5]。其中，全封闭矩形式声屏障已在部分工程中推广应用[6]，如：沪杭客专线闵行段经林水美地苑小区段、杭长线金华市东上小区附近段以及武汉市轨道交通1号线从宗关至黄浦路段等。针对高铁声屏障的研究，当前研究主要关注声屏障的材质以及外形等因素对其降噪性能的影响。LEE等[7]基于统计分析，对比金属声屏障与塑料声屏障的吸声效果差异；ZHANG等[6]对比研究了半封闭声屏障与直立板声屏障的隔音效果，结果表明：半封闭声屏障的隔音效果比直立板声屏障的隔音效果更佳，其中降噪量高达6 dB；LEE等[8]对新加坡和台湾的地铁声屏障降噪性能进行了对比研究，结果表明：悬臂声屏障比直立板声屏障的降噪效果更佳。有部分研究者关注到声屏障在列车风作用下的气动压力问题，并展开了一系列相关研究。例如：DU等[9]通过开展1:20的动列车模型试验，分析了由列车运行引起的高度分别为0.125 m和0.25 m的直立板声屏障气动压力分布特征；XIONG等[10-11]针对由列车通过所引起的直立板声屏障内侧气动压力的脉动特征展开了一系列现场实测研究；MENG等[12]采用STAR计算流体软件，基于延迟分离涡模拟方法(IDDES)建立1:16的列车-直立板声屏障模型，研究了车头鼻尖长度对声屏障的压力影响规律。上述研究表明：高速列车运行对直立板式声屏障的气动冲击作用不容忽视。事实上，声屏障在强横风作用下同样易产生剧烈振动，严重时甚至可能发生螺栓松动、断裂及声屏障组件板破坏等现象。相对于直立板式声屏障，全封闭矩形式声屏障具有更大的迎风面积；同时，为缓解高速列车进(出)声屏障时产生的微气压波效应，往往需要在其进、出口段的顶部进行开孔处理[13-15]，因此该类声屏障的抗风性能及其间的气动性能差异将成为高铁基础设施结构设计中务必考虑的问题。然而，鲜有研究者关注横风作用下全封闭矩形声屏障气动性能。本文参照中南大学轨道交通安全教育部重点实验室1:16.8的列车-声屏障动模型试验装置，建立相同比例的横风-列车-桥梁-声屏障三维精细化CFD数值仿真模型，采用大涡模拟(LES)方法分析横风作用下2种全封闭矩形式声屏障的气动压力以及流场结构；基于本征正交分解(POD)理论，采用Matlab软件分别对横风作用下2种声屏障的绕流流场进行分解，探讨各阶模态对湍动能的贡献，以期为全封闭矩形式声屏障的抗风设计提供理论依据。

1 CFD数值模拟

1.1 大涡模拟(LES)理论

大涡模拟(LES)方法[16]的基本思想是对Navier-Stokes方程进行某种过滤，对大尺度涡结构进行直接求解，而将小于过滤尺度的湍流采用现有模型加以刻画。其求解过程如下：

式中：G(r，xi)表示滤波函数；和分别表示过滤后分解得到的速度和压力；表示亚格子尺度应力张量(即残余应力)，

1.2 模型概况

数值模型计算域如图1(a)所示，以列车模型高度H(H=0.23 m)为度量单位，计算域宽43.5H，高17.8H，长386.9H。其中，全封闭矩形式声屏障位于计算域中部的桥梁上，其长(L)、宽和高分别为106.1H，3.1H和2.2H；声屏障底部的桥梁模型参照我国高铁线路上使用频率最高的32 m预应力混凝土简支箱梁按1:16.8比例进行缩尺(该缩尺比例已满足相关动模型试验规范[9]的规定)，宽和高分别为3.1H和0.8H，桥面距离地面高度为4.4H。对于工况2，声屏障每端顶部的开孔长度为13H，开孔宽度为1.5H。横风垂直于线路方向，风速为15 m/s，此时列车(CRH380B型)已停靠于声屏障的中部。气动压力监测点位于声屏障迎风面的内、外两侧，如图1(b)所示。

图1 几何模型及测点布置Fig. 1 Geometric model and arrangement of measuring points

模型中使用的边界条件主要有3类。其中No-slip Wall用于列车表面、声屏障表面、桥面以及试验室上下壁面等，Velocity-inlet被用于来流面，Pressure-outlet被用于计算域的前、后两端以及来流面的对立面。

网格模型如图2所示，计算域主要采用Poly-Hexcore类型的网格进行离散，其中声屏障的网格尺寸范围为0.02～0.03 m，设置5层附面层，第1层网格厚度为0.002 m，相应的y+值处于1～5的范围(此时可保证第1个内节点处于黏性底层的范围内，即配置到旺盛湍流区域)。网格单元总数量约为1 500万，并采用Fluent中的LES方法进行瞬态求解，时间步长设置为10-4s。

图2 网格模型Fig. 2 Geometric model

1.3 数据处理

为使压力结果具有可对比性，将数值计算所得的压力数据按式(4)进行无量纲化处理[17]。

式中：CP为压力系数；ρ为空气密度；Va为来流风速；Pi为计算得到的测点压力值；P0为环境的参考气压。

1.4 模型验证

为验证数值模型的可靠性，将动列车模型试验结果与相应的数值计算结果进行对比。在该试验中(如图3)，列车模型运行速度为350 km/h(经估算，相应的雷诺数不低于2.5×105，满足欧盟标准的相关规定[9])，无横风作用，采用Honeywell DC030NDC4微差压传感器获取声屏障内侧(近车侧)测点#1-2，#5-2以及#9-2的压力时程数据，并采用1阶低通巴特沃斯滤波器对原始数据进行滤波处理，滤波截止频率为20 Hz；数值计算仍采用LES湍流模拟方案，横风风速设置为0 m/s，声屏障尺寸和车速等其余条件均与试验保持一致，二者相应结果对比情况如图4所示。

图3 动模型试验装置Fig. 3 Device for moving train model test

由图4可知，数值模拟所获得的测点气动压力时程曲线的脉动规律与相应试验结果基本吻合，压力幅值相差在5%以内。因此，可认为该数值模型以及模拟方案是可靠的。

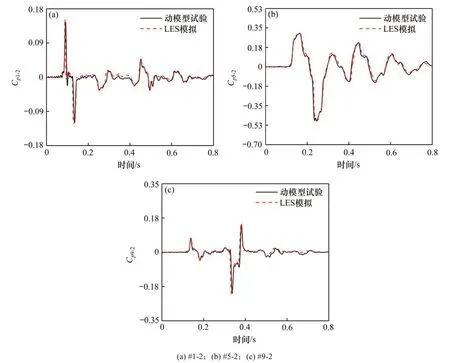
图4 结果对比Fig. 4 Comparison of results

为进一步验证横风作用下声屏障表面压力结果的可靠性，参照敬海泉等[17]中缩尺比为1:15的全封闭弧形声屏障风洞试验装置，基于本文的数值方法建立了一个与之对应的数值模型(如图5(b))，并取声屏障中部断面上外侧的压力系数作为验证指标。图5(c)为风洞试验结果与相应的数值模拟结果的对比，由图可知：二者结果最大差异处位于63°附近，相差仅为6.2%，可认为本文的横风作用下的数值模拟结果仍是可靠的。

图5 横风下声屏障外侧压力结果验证Fig. 5 Verification of the results of aerodynamic pressure outside the noise barrier under crosswind

2 本征正交分解(POD)方法

本征正交分解(POD)是一种识别湍流特征和关键事件的重要方法[18]。进行POD模态分解首先需要从各瞬态快照流场U(ξ，t)中分离出平均速度场U(ξ)，后续的流场分解主要针对流场脉动分量x(t)展开。流场脉动分量x(t)计算公式如下：

随后计算给定流场数据的特征值λj与特征向量ψj，计算公式如下：

式中：R为流场脉动分量x(t)的自相关矩阵，Rn为n维向量空间。可根据下式计算：

矩阵X表示m张快照数据的组成的合矩阵，如下式所示。

求取以上特征值与特征向量后，POD模态通过下式构建：

式中，特征值λj为每一阶POD模态的湍流动能，通过特征值大小可确定每一阶POD模态对湍流流场的贡献程度。通常，前r阶POD模态往往占据流场90%以上的湍流动能，因此仅需保留r(r

通过以上方法即可有效将高维(n维)流场转化为仅包含r阶模态的降阶流场。POD系数计算公式如下：

为获得可靠的POD模态，POD分解的采样频率为1 500 Hz，瞬时采样数为1 000帧。

3 结果分析

3.1 气动压力时程

图6为横风风速为15 m/s时，2种(工况1和2)全封闭矩形式声屏障在同一高度(H)上内侧与外侧各测点的压力时程曲线，表1给出了各测点处压力均值和相应湍流强度的统计情况。图7则进一步给出了2个工况中C1和C5截面上不同高度测点的压力时程曲线。

表1 2工况中各测点处的压力均值与湍流度统计Table 1 Mean pressure and turbulence intensity at each measuring point in the two cases

图6 各截面测点的气动压力时程曲线Fig. 6 Time-history curves of the aerodynamic pressure at the measuring points of each section

由图6和图7分析可知：

图7 C1和C5截面测点的气动压力时程曲线Fig. 7 Time-history curves of the aerodynamic pressure at the measuring points of C1 and C5 sections

全封闭式声屏障受横风作用时，尽管来流横风的风速恒定，内、外侧测点气动压力均出现剧烈波动，且内侧压力均值为负，外侧压力均值为正。2种全封闭式声屏障所受的气动压力均表现出剧烈的脉动特性，且湍流强度在纵向分布上均呈现出两端小、中间大的规律，内侧测点的湍流强度均高于外侧相应测点，该差异在C5截面上表现最为显著。同一截面上不同高度处测点的压力时程是几乎吻合的，说明在横风来流均匀恒定的条件下，全封闭矩形声屏障所受的气动压力分布具有显著的二维特性。

相对于工况1，在进、出口顶部开孔的全封闭矩形式声屏障内侧测点的负压值进一步降低，且湍流强度进一步升高。以C5截面为例(表1)，内侧测点压力均值降低82%，湍流强度升高114%。因此，全封闭矩形式声屏障在进、出口顶部开孔将导致横风风致振动加剧。

3.2 流场特性

图8分别为2种声屏障的横断面与水平面瞬态流场结构对比图。由图8分析可知：

在横断面上，2种工况中桥梁翼缘板下部以及声屏障顶部隅角处均出现了相似的涡量局部增大现象。这是因为上述位置的局部结构相同，流场经过这几个位置时受到阻碍，风速出现扭转应力增大现象，从而导致涡量增加。除S1和S5截面外，2种全封闭式声屏障的流场结构高度相似，即：顶板出现正涡量区，背风侧由于横风绕流出现1至2个主涡旋。2种工况的流场结构差异之处主要体现在进出口段(S1和S5截面)，即：工况1顶部出现与顶板宽度相当的大尺度涡旋结构，而工况2中由于声屏障两端结构未封闭，其顶部难以形成大尺度涡旋结构。此外，2种工况中，声屏障的内部流场均出现异于S2-S4截面的非源流性不规则流场，然而矩形进出口开孔式声屏障内部则呈现更为剧烈的湍流现象，这可能是进、出口开孔式声屏障内部测点压力均值与脉动程度均大于未开孔的全封闭矩形式声屏障相应值的原因。

在水平面上，2种声屏障绕流流场的相似之处表现在：迎风侧的都处于均匀流场中，背风侧流场紊乱无序，涡量分布也无规律可循。2种声屏障的两端均出现端部绕流现象，从而引起进出口段的涡量分布呈现无序性。2种声屏障流场的主要差异在于：相比于工况1，进、出口开孔式声屏障出现端部绕流现象的纵向区域更长，这是矩形进出口开口式声屏障压力两端小中间大的主要原因。

3.3 POD模态特征

图9给出了2种工况条件下对应于图8(a)中的声屏障S1和S3截面的前10阶模态能量占比图。由图9分析可知，对于2种全封闭矩形式声屏障，随POD模态阶数增加，其绕流的湍流能占比均呈急剧下降，且1阶和2阶湍流能占比之和均达到百分之95%以上。S1截面的2阶湍流能占比高于S3截面相应值，说明全封闭矩形式声屏障进、出口段横风绕流的2阶模态对湍流的贡献大于中间截面。