有源钳位四电平能馈变流器预测电流控制

2023-02-24向超群范子寅王成强席振周瑞睿成庶于天剑

铁道科学与工程学报 2023年1期

向超群，范子寅，王成强，席振，周瑞睿，成庶，于天剑

(1. 中南大学交通运输工程学院，湖南长沙 410075；2. 中车长春轨道客车股份有限公司，吉林长春 130062)

现今，我国的城轨交通建设得到快速推进，大批城轨线路投入运营，同时地铁也消耗了大量能源以维持运营。地铁在站间运行时，由于运行距离较短，需要频繁地启动和制动，导致大量的能量耗散[1]。其中，制动过程采用电制动的方式，耗散的再生制动能可达牵引能耗的40%[2]，该部分能量若直接接入电网，会在短时间之内抬高电网电压，对电网造成破坏。若能通过适当地处理回收这部分能量，则不仅保护了电网，还可以提高能量利用率，实现节能减排。一个可行的能量回收方案是通过变流器进行能量回馈[3]，要实现该方案，需设计相应的变流器逆变电路和控制算法。对于逆变电路，自1981年提出三电平中点钳位型逆变电路的拓扑模型[4]以来，多电平逆变电路在能馈领域得到了广泛应用[5-6]，其电平数多的特点，不但提高了输出电流的质量，还有效降低了电路中有源开关的断态电压上升率[7]，更好地保护了电路元件。学者们对多电平逆变电路在地铁能馈场景下的应用进行了深入研究。沈石秀等[8]提出了新的三电平中点钳位型逆变电路的控制算法与中点电压平衡方案。周湘杰等[9]设计了一套由8个三电平逆变模块并联的能馈装置。陈学农等[10]通过大量的仿真分析和实验验证，成功地将三电平中点钳位型逆变器的关键控制技术应用于地铁能馈系统中。但是，迄今为止的研究大多集中于三电平逆变电路，对于更多电平数逆变电路的研究较少。更多电平的逆变电路可进一步降低功率器件的耐压等级，增加开关组的冗余状态数，有利于提高输出电流的波形质量，提升电路稳定性。但是，电平数的增加也会带来中点电压平衡和元件热管理方面的困难[11]，相关的解决方案仍有待研究。对于控制算法，目前常用于多电平逆变电路的是脉冲宽度调制算法(pulse wide modulation, PWM)和模型预测控制算法(model predictive control, MPC)。PWM算法原理简单，但是运算复杂，脉冲信号的调制会产生较大的运算量，控制信号输出频率的上限较低[12]。另外，该算法较难适应复杂的电路拓扑结构，未被许多新提出的逆变拓扑采纳。目前，地铁能馈领域对逆变电路的研究重点是在三电平逆变电路，这类电路的拓扑模型提出时间较早，PWM算法具有良好的适应性[13]。但若应用于更高电平数的逆变电路中，该算法的适用性将下降。MPC算法在上世纪70年代被提出，随后在石油、电力和航空等工业领域创造了诸多成功案例。该算法原理复杂，但是运算简单，虽然为逆变电路建立数学模型的过程较为复杂，但是一旦完成建模，即可根据输入的参考波形快速得到输出结果，展现出良好的应用前景[14-15]。此外，得益于数学建模学科的发展，该算法适用于各种复杂拓扑结构，只需为拓扑结构建立正确的数学模型，就可实现电路输出的预测。目前，地铁能馈领域对该算法几乎没有研究。增加电平数可以提升逆变电路的性能，但同时也会增加控制的难度。在地铁能馈大功率中压工况下，与三电平相比，四电平拓扑输出谐波更低，同时电路元件的数量和控制复杂度小于五电平逆变电路[16]。由于有效降低了功率器件耐压等级和输出谐波，四电平拓扑可提高设备能量密度，并减小滤波器件的体积和重量。综合考虑性能、成本和可行性等因素，本文提出一种有源钳位四电平拓扑模型，弥补了地铁能馈领域四电平逆变电路的研究空白。对于电平数增加带来的电容电压平衡困难的问题，提出一种电流预测控制算法，通过分析电流流向和设计代价函数，解决电容电压平衡的问题。电流预测控制算法利用了预测控制多目标规划的优势[17]，既可保证输出电流的质量，又可平衡电容电压，应用于地铁能馈领域是一大创新。后续对电路拓扑的阻感负载模型和并网模型进行实验或simulink仿真，验证了拓扑模型和控制算法的有效性，以及在地铁能馈领域应用的可行性。

1 有源钳位四电平拓扑

1.1 传统的四电平中点钳位型逆变电路

传统的四电平中点钳位型逆变电路如图1所示，电路的直流母线包含3个相同的电容，电路的每个桥臂包含4个钳位二极管和6个有源开关。

图1 传统的四电平中点钳位型逆变电路Fig. 1 Traditional four-level neutral point clamped inverter circuit

电路中，3个直流母线电容将电源电压Vdc三等分，形成4个输出电平——Vdc，2/3Vdc，1/3Vdc和0。4个钳位二极管和6个有源开关相互配合，通过设定有源开关的通断状态，实现输出电压电平的调节。其中，当开关S2，S3和S4接通，S1，S5和S6断开时，钳位二极管将开关S1与S2或S4与S5之间的电势钳定在2/3Vdc；当开关S3，S4和S5接通，S1，S2和S6断开时，钳位二极管将开关S2与S3或S5与S6之间的电势钳定在1/3Vdc；其他时候，钳位二极管未起作用。由于数量众多的钳位二极管的存在，电路工作时热损耗过大，平衡二极管与开关之间的受压状况比较困难，造成电路工作成本上升，稳定性下降。同时，钳位二极管的作用又很有限。

1.2 有源钳位四电平逆变电路

1.2.1 电路拓扑模型

为解决大量钳位二极管所带来的麻烦，本文参考WANG等[18]提出的拓扑模型，采用如图2所示的新型有源钳位四电平逆变电路。新电路弃置了全部的钳位二极管，改为通过有源开关T型连接的方式实现电势的钳位，同时新电路未增加有源开关的数量。总体上说，新电路在保留全部变流功能的前提下，减少了元件总数，改善了元件的受压条件，并且降低了能耗。

1.2.2 输出电平的控制原理

在直流母线电容C1，C2和C3的两端标注O0～O3共4个点(如图2)，由于C1，C2和C3完全相同，O0～O3处的电势分别为0，1/3Vdc，2/3Vdc和Vdc。电路工作时，O0～O3之间相互不允许短路，故在同一时刻，直流母线与每个桥臂的输出端之间只能有唯一的通路。通路两端电势相等，故桥臂输出端的电势总是与O0～O3中的一处相等，换言之，桥臂可能输出4种电平的电势，并且它们有固定的值。桥臂具体输出哪一种电平的电势，则与桥臂上有源开关的通断状态组合有关。

图2 本文的有源钳位四电平逆变电路Fig. 2 Four-level active-clamped inverter circuit of this paper

开关状态组合决定了电流在桥臂中的流动路径，进而决定了输出端的电平等级。具体而言，开关状态组合与输出端的电平等级之间存在图3所示的关联。

当开关S1和S2接通，S3，S4，S5和S6断开时(如图3(a)所示)，桥臂输出端与O3处连通，输出端电势与O3处相等，为Vdc；当开关S2和S5接通，S1，S3，S4和S6断开时(如图3(b)所示)，桥臂输出端与O2处连通，输出端电势与O2处相等，为2/3Vdc；当开关S3和S6接通，S1，S2，S4和S5断开时(如图3(c)所示)，桥臂输出端与O1处连通，输出端电势与O1处相等，为1/3Vdc；当开关S3和S4接通，S1，S2，S5和S6断开时(如图3(d)所示)，桥臂输出端与O0处连通，输出端电势与O0处相等，为0。根据上述分析，可以列出开关状态组合与输出电平的关系如表1所示。

表1 开关状态组合与输出电平的关系Table 1 Relationship between switch state combination and output level

图3 电流在桥臂中的流动路径Fig. 3 Current flow path in the bridge arm

2 电容电压平衡分析

图2所示的电路拓扑模型中，在理想状况下，O3～O0点的电势应分别为Vdc，2/3Vdc，1/3Vdc和0，电容C1，C2和C3的电压降均是定值1/3Vdc。但在实际应用中，电容电压由电容两端携带的电荷量所决定。电路工作时，O3～O0点不断有电流流入或流出直流母线，C1，C2和C3总是处于充放电状态，其两端携带的电荷量会随时间改变，故C1，C2和C3的电压不是定值。

不同的开关状态组合会使C1，C2和C3处于不同的充放电状态，因而对3个电容电压造成的影响也不同。为了使电容电压尽可能地接近理想值(即电压平衡状态)，需分析各开关状态组合对电容电压平衡的破坏程度，并在控制算法中尽量采用破坏程度较小的开关状态组合。

电容电压相对于理想值的改变量是衡量破坏程度的指标，计算这一指标的关键是合理地预测每种开关状态组合运行一个单位时间后3个电容的电压值。设现在时刻为k时刻，则需要预测k+1时刻的电容电压值V(k+1)。

如图4所示，实际应用中，通过实测的方式可获得k时刻3个桥臂的输出电流值Ia(k)，Ib(k)和Ic(k)以及直流母线的电流值Idc(k)，在O3，O2和O13处应用基尔霍夫电流法则，可以求得k时刻通过3个电容的电流值IC1(k)，IC2(k)和IC3(k)分别为：

图4 电流流动情况示意图Fig. 4 Schematic diagram of current flow

其中，IO1(k)，IO2(k)和IO3(k)分别为：

式中：Ga，Gb和Gc分别为3个桥臂的输出电平。

计算出IC1(k)，IC2(k)和IC3(k)后，可以进一步计算V(k+1)。在一个理想电容中，其储电量Q与电压U的比值总是恒定为电容量C，即当电容储电量增加dQ时，电容电压相应地会增加以维持将dQ=Idt代入上式中进行变换，可得：

利用前向欧拉逼近将导数离散化，得到：

变换式(3)即可得到电容电压值的预测公式：

实际计算时，代入Cx电容k时刻的电压实测值VCx(k)以及算得的电流值ICx(k)，即可计算出k+1时刻Cx电容的电压预测值VCx(k+1)。

3 预测电流控制算法

本文提出的预测电流控制算法是模型预测控制算法中的一类，该算法基于以下原理。

1) 电路中开关的数量有限，这些开关的状态组合也是有限的。

2) 每一种开关的状态组合作用于电路中，电路的3个桥臂输出端都会输出特定的电压，而这3个输出电压作用于与3个桥臂相连的负载上，则会相应地得到3个负载电流。

3) 在同一时刻，使用不同的开关状态组合，电路的负载电流可能不相同。而把所有x种开关状态组合分别作用于该时刻电路中，将会得到不超过x种情况的负载电流。在这些情况中，有一种情况的负载电流最接近期望。

4) 将最接近期望的情况对应的开关状态组合输出，即得到上述时刻的算法结果，输出的信号即开关控制信号。

算法通过使用的开关状态组合和电路当前时刻的情况，预测电路下一时刻的负载电流，并通过比较选出最接近期望的负载电流。预测和比较是本文所提算法的重要部分，在预测负载电流时，需要考虑输出电压矢量和负载模型，而在比较最优情况时，则引入了代价函数的概念。此外，还应考虑电流对直流母线电容电压的影响。

3.1 代价函数设计

预测电流控制的目标是使下一时刻(k+1时刻)电路输出的负载电流尽可能地接近参考电流。为量化k+1时刻负载电流与参考电流的接近程度，现设立代价函数g。代价函数g通过衡量不同开关状态组合对电流接近程度的影响，找出最佳的一组开关状态组合，作用于逆变电路。

设k+1时刻负载电流的预测值为Ip(k+1)，参考电流为Ir(k+1)，则Ip(k+1)与Ir(k+1)的差值是衡量负载电流与参考电流接近程度的最主要因素。Ir(k+1)来自控制系统的给定，通过将3个桥臂预设的参考电流值和进行Clark变换，可算出复数矢量Ir(k+1)。Ip(k+1)则需根据选定的开关状态组合，通过下列计算得出。

设k时刻负载电流的实测值为I(k)，选取的电压矢量为V(k)，负载反电动势为e(k)，则有：

式中：I(k)，V(k)和e(k)均为复数矢量，是3个桥臂的标量数值通过Clark变换的结果，其中，V(k)根据选定的开关状态组合查表得出，e(k)则需经以下计算求出。

对于阻感负载模型，有：

对于并网模型，有：

式中：e(k-1)，e(k-2)和e(k-3)分别为此前3个时刻的负载反电动势值。

得到Ir(k+1)和Ip(k+1)后，令

式中：Dis是表示Ir(k+1)和Ip(k+1)接近程度的指标，是代价函数g的主要组成部分。现实中，如前文所述，直流母线电容电压不是一个固定的理想值，通过上述方法计算出的Ip(k+1)并非精确值，故在设计代价函数g时，还需考虑电容电压的平衡问题。

根据式(4)，算出k+1时刻电容电压的预测值并令

式中：Dif即衡量开关状态组合对电容电压平衡的破坏程度的指标；为电容Cx的理想电压值。

Dis的结果越小，说明负载电流预测值越接近参考电流值；Dif的结果越小，说明电容电压平衡的破坏程度越轻。为综合考虑2式的结果，将代价函数g表示为：

式中：λ为电容电压平衡因素的权重。

3.2 算法流程图

如图5所示，本文提出的预测电流控制算法流程如下。

图5 预测电流控制算法流程图Fig. 5 Predictive current control algorithm flowchart

1) 测取k时刻直流母线电流、三相输出电流和3个电容电压的值。

2) 估算k时刻的负载反电动势。

3) 分别预测64种开关状态组合在k+1时刻的输出电流和电容电压，并计算代价函数。

4) 比较64种开关状态组合的代价函数计算结果，找到结果最小的开关状态组合，该组合即为k+1时刻算法的输出。

4 仿真与实验验证

对所提出的有源钳位四电平拓扑分别进行并网模型的仿真测试和阻感负载模型的实验验证。需要说明的是，实际实验中并网电流的幅值高达数十乃至上百安培，超出实验设备可承受的负载范围，故采用小电流阻感负载实验代替并网仿真的验证。

4.1 并网模型的仿真验证

如图6所示，并网时，逆变电路的参考并网电流的周期、幅值和相位与电网电流一致，其中电网电流的相位可利用锁相环获取。在仿真验证时，设RL滤波电路的参数为R=1 Ω，L=5 mH，直流母线电容C=3 mF，直流母线电压Vdc=1 700 V，电网电压幅值为850 V。该设定与地铁能馈装置的实际工况较接近。图7～图13为并网模型的仿真结果。

图6 并网仿真原理图Fig. 6 Grid-connected simulation schematic

图7 并网仿真的电容电压图(Im=100 A)Fig. 7 Capacitor-voltage plot for grid-connected simulation

图7～图9展示了电网电流幅值为100 A时的仿真结果。在此工况下，直流母线电容电压平衡良好，并网电流与电网电流波形相近。通过对并网电流进行FFT分析，发现其总谐波畸变率(THD值)为3.87%，低于5%，达到并网要求，说明逆变电路具有应用于实际的可行性。

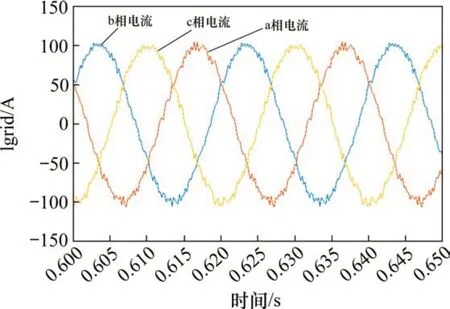
图8 并网仿真的负载电流图(Im=100 A)Fig. 8 Load Current plot for grid-connected simulation(Im=100 A)

图9 FFT分析结果(Im=100 A)Fig. 9 FFT analysis results (Im=100 A)

为探究逆变电路在更多工况下的并网工作情况，对电网电流幅值为75 A和150 A的情况进行仿真。从图10～图13可发现，在2种不同电流设定下，直流母线电容电压均较稳定，本文提出的控制方法在并网时具有出色的电容电压平衡能力。并网电流具有较好的跟踪特性，但在幅值为150 A时，并网电流的波形质量明显得到提高，反映出逆变电路在调制度较高的工况时，输出效果更佳。

图10 并网仿真的电容电压图(Im=75 A)Fig. 10 Capacitor-voltage plot for grid-connected simulation(Im=75 A)

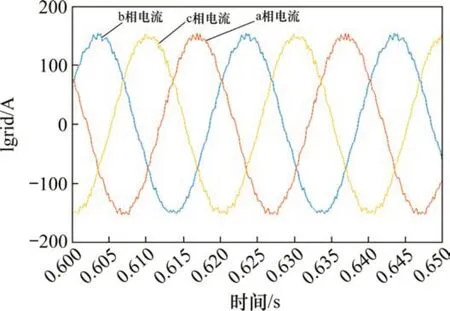
图13 并网仿真的负载电流图(Im=150 A)Fig. 13 Load Current plot for grid-connected simulation(Im=150 A)

图14显示了并网负载突变时电容电压的平衡结果。在第0.5 s时，电网电流突然从75 A上升至100 A(如图14(b)所示)，电容电压的变化轨迹也随之改变(如图14(a)所示)。电容电压的变化与代价函数权重的值有关，若权重设置合理，则电容电压可在负载突变一段时间后逐渐趋于平稳，反映出电路具有抵御突变的能力。

图14 并网仿真的变负载响应Fig. 14 Variable load response of grid-connected simulation

4.2 阻感负载模型的实验验证

搭建图15所示的实验平台，取负载电阻R=10 Ω，负载电感L=10 mH，开关频率10 kHz，得到图16～20所示的实验结果。

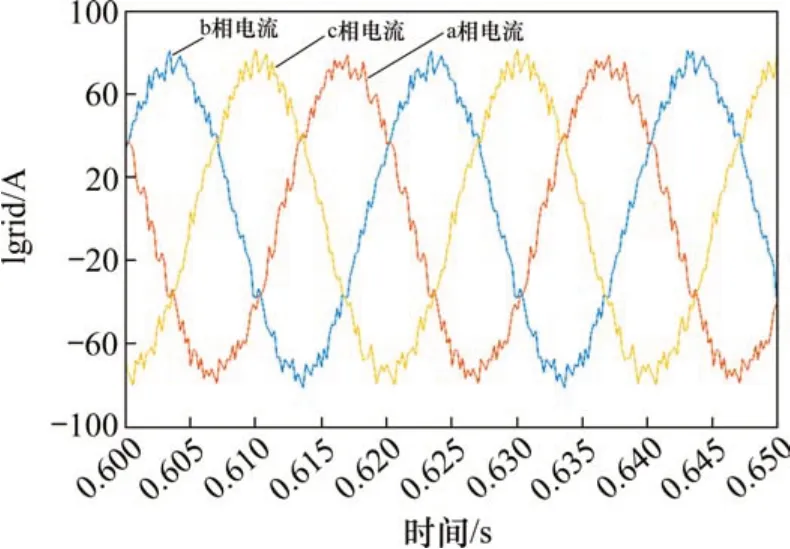
图11 并网仿真的负载电流图(Im=75 A)Fig. 11 Load Current plot for grid-connected simulation(Im=75 A)

图12 并网仿真的电容电压图(Im=150 A)Fig. 12 Capacitor-voltage plot (Im=150 A)

图15 实验平台Fig. 15 Experiment platform

图16设直流母线电压为120 V，负载电流幅值2 A。在此设定下，直流母线电容电压较稳定，电压平衡效果良好。负载线电压波形呈现出明显梯度，可看出用到了2/3Vdc，1/3Vdc和0这3个电平等级。负载电流的幅值与预设值基本相等，波形抖动较小，体现出逆变电路对输出电流优秀的调制能力。

图16 120 V-2 A实验结果Fig. 16 120 V-2 A experimental results

图17和图18设直流母线电压为150 V，负载电流幅值分别为2 A和7 A，测试逆变电路在更高的电压和更大的电流工况下的工作情况。在以上2种设定下，直流母线电容电压的波动均未超过2 V，电容分压稳定。当负载电流幅值为7 A时，负载线电压显示出4个电平梯度，分别为Vdc，2/3Vdc，1/3Vdc和0，负载电流依然得到良好调制，波形质量高，此时THD值为4.74%，反映出逆变电路处于较好的工作状态。