基于BP神经网络的机电产品清单数据智能补全算法研究*

丁永新，李 涛，郭志威，张洪潮

（1.大连理工大学机械工程学院，辽宁大连 116081；2.大连理工大学重大装备设计研究所，辽宁大连 116081；3.德克萨斯理工大学工业工程系，美国德州 TX76001）

0 引言

近些年，机械制造业在迅速地发展，与此同时造成了非常严重的环境问题，如全球变暖、生态恶化、水体污染、水体富营养化等，严重阻碍了可持续发展的进程[1-2]。经研究表明，机电产品在制造和使用阶段是影响全球环境生态的最重要因素之一，据统计，机电产品的生产制造过程产生污染物占到了全球污染物排放量的73%以上[3]。而生命周期评价（Life cycle assessment）是可以从产品的全生命周期角度量化潜在环境影响的方法，可以用来评价产品设计方案中表达的产品生命周期内经历的环境影响，是一个有效的方案决策支持方法[4]。但是由于生命周期评价所需的清单数据繁多，并且追逐源头所需的物力和精力巨大，因此进行生命周期周期评价的最难的问题就是清单数据中缺失数据的填充。

刘云等[5]利用对称加权算法对数据分析中数据集缺失矩阵进行补全，通过正则化方法进行低秩矩阵的分解补全结合块坐标下降和交替最小二乘法进行数据补全。杨亚洲等[6]基于k-means聚类方法的曲线按比例伸缩置换法提出了一种缺失数据的补全算法用于填充历史电力负荷缺失的数据，与传统的插值法和平均日负荷曲线补全法相比，预测的准确性提高了很多。刘琚等[7]提出了一种基于多向延迟嵌入的平滑张量补全算法分类框架用于补全BraTS脑胶质瘤影像数据，并于7种基线模型进行了比较，得到最后的准确率高达91.31%。

本文通过分析机电产品物料清单的数据类型，借助莱温斯坦距离和神经网络提出了一种清单数据智能补全方法，可用于LCA软件在评价过程中自动补全缺失的数据。

1 生命周期评价

生命周期评价可以对机电产品的全生命周期阶段所造成得影响进行定量分析。经过很多年的发展己经在产品的生产制造中发挥作用[4]。其过程主要包括4个步骤：目的与范围的确定、清单分析、影响评价和结果解释。

（1）目的和范围的确定

确定评价的LCA评价目的，根据评价的机电产品的特点和目的划分评价范围。

（2）清单分析

清单分析是最浪费时间和精力的阶段，即对机电产品整个生命周期中的输入输出进行统计和量化，如果清单数据存在数据缺失则需要对评价范围进行修改。

（3）影响评价

影响评价指根据清单分析的结果，对机电产品生命周期中潜在的环境影响进行量化、分析和评价。

（4）结果解释

结果解释是对机电产品进行分析后得到结论和建议的阶段，在这一阶段中对重要的输入、输出、评价方法进行不确定性检查以及选择性评价，并对结论和建议予以说明。

然而以上步骤的顺利执行都依赖于清单数据的完整性和准确性，如果存在清单数据缺失，那么LCA分析的结果会存在一定准确性的问题。因此本文根据机电产品物料清单的特征，基于莱温斯坦距离和神经网络提出一种清单自动补全算法，可以实现案例的重复利用，减少清单数据收集的准备工作。

2 基于BP神经网络的补全算法

2.1 物料清单

机电产品的物料清单指进行生命周期评价的数据清单，其中包括了机电产品的生命周期信息，比如：零件名称、重量、产地、零件型号、材料、运输距离、运输方式、工艺、回收等信息。加上和这些信息相关的其他信息一共11项，如表1所示。

表1 影响相似度的11项参数信息

2.2 BP神经网络及数据补全

BP神经网络是由科学家Rumelhart和McClelland提出的概念，是一种根据误差反向传播进行训练的多层前馈网络[8]，主要思想是梯度下降，利用梯度搜索技术使得神经网络的输出期望值和输出真实值的差值的均方差最小。

BP神经网络结构包含一个输入层、一个或多个隐含层和一个输出层（如图1所示），通过权值和阀值将相邻层的神经元连接起来。其中隐含层所包含的神经元数量需要通过公式计算得到。

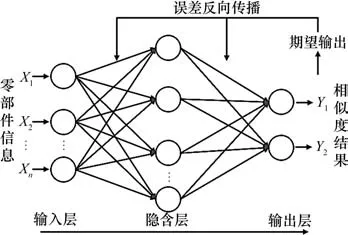
图1 BP神经网络三层结构图

结合2.1节，一个零部件的信息一种由11种，但是因为每一种信息在相似度计算时所占的权重不同，所以并不能直接加和，同时因为BP神经网络天生就可以用于计算输入参数的权重信息，因此本文采用BP神经网络来进行相似度结果的计算。

因为三层的神经网络有较好的函数逼近的作用，并且网络结构简单，因此本文采用三层BP神经网络结构，其计算相似度补全数据的流程如图2所示。

图2 清单数据补全流程

2.3 BP神经网络设计

2.3.1 训练样本选择

训练样本来自零件库。每条样本包含3大部分，当前零件的11项参数信息、比较对象的11项信息以及两个零件是否一致，共计220条数据。

2.3.2 输入参数处理

因为输入的参数含有文本类型（如材料、运输方式、工艺方式等），也有含有数字类型的数据（如运输距离、回收百分比等），因此这11项参数并不能直接输入神经网络，需要先进行文本类数据处理，数值类数据处理。

（1）文本类数据相似度计算

文本数据相似度的计算，常用的计算文本相似度的方法包括欧氏距离、曼哈顿距离、闵科夫斯基距离、余弦夹角相似度以及切比雪夫距离等[9]，但是大多都针对复杂文本，本文所使用的文本多是单个词语不包含主谓宾等句子结构以及不需要进行分词处理，因此本文计算文本的相似距离采用基于字符的编辑距离的一种莱文斯坦距离。

莱文斯坦距离即由一个字符串变成另一个字符所需的最少操作次数。允许的操作包括删除字符、替换字符、插入字符[10]。在数学上，如式（1）所示，leva,b(i,j)是字符串a的前i个字符和字符串b的前j个字符之间的距离。

输入层的参数可能受文本类数据长度的影响，编辑距离会大小不一，而变化幅度大的输入值会增加权重和阈值的调节难度，因此需要将样本数据归一化到[0，1]之间。本文所采用的归一化方法如式（2）所示。Xmin代表字符串A和B之间最少字符个数，Xmax代表字符串A和B之间最多字符个数，X′代表归一化结果。

（2）数值型数据相似度计算

对于数值型数据，计算当前值和目标值之间的相对误差，然后1减去相对误差即为该参数的相似度[11]，即式（3）所示，其中A代表当前值，B代表目标值，Dnum表示A和B之间的相似度。

2.3.3 激活函数、损失函数选择

激活函数（Activation Function）是运行在人工神经网络的神经元上的数学函数，它负责把输入端映射到输出端。本文的算法所采用的激活函数为Sigmoid函数[12]，该函数是生物学中常见的S型函数，也称逻辑斯谛回归函数。如式（4）所示：

损失函数是用来评价算法模型的真实值和预测值之间的差异程度，损失函数选择的越好，算法模型的性能也就越好。不同的模型采用的损失函数也不是固定不变的，根据实际应用场景，本文的损失函数选择交叉熵损失函数，如式（5）所示：

2.3.4 输入层、输出层、隐含层数量

输出层对应着输入参数的个数，有几个参数，输入层的结点个数就设置几个，根据对输入样本的分析，输入层神经元的数量设置为11个，分别对应11项参数信息。

输出层对应着预测的结果，因为该神经网络预测的模型的结果只有两个，一致和不一致，因此输出层的神经元的数量设置为2个，分别对应一致和不一致两个结果。

隐含层的设计是训练神经网络的最为重要的一环，隐含层最主要的就是用来确定神经元的数量。隐含层神经元数量太多会使神经的网络学习时间变长，太少会使非线性网络逼近的精度降低，与此同时也会使模型的容错性误差增大。一般通过式（6）来确定神经元的结点的数量，即：

式中：n为输入层神经元数量；l为输出层神经元数量；m为隐含层神经元数量；a通常取[1，10]之间的常数。

计算时，m的值可以用四舍五入法进行相应的调整。分别测试在达到98%的准确率条件下隐含层不同神经元数量的训练次数和训练时间，训练结果如图3所示。因此隐含层神经元数量确定为10个。

图3 不同隐含层神经元数量达到阙值的迭代次数和时间

2.4 实验验证

原始数据集即表3（测试数据和补全数据一致），手动删掉一些信息（文本类数据填null，数值型数据填0），测试数据如表2所示。将表2的信息输入神经网络进行补全测试。

表2 缺少信息的清单数据

补全后的数据如表3所示，所有空缺数据均已补全，补全零部件的信息在备注里会提示*，没有缺失数据备注就为空。和原始完整的数据进行对比，发现该相似度计算模型补全了所有相似信息并且正确率达100%。

3 结束语

本文通过分析机电产品的数据清单的特征，将缺失数据分为文本型数据和数值型数据，针对不同类型的数据分别采用不同的相似度就算方法，通过一个设计好的三层的BP神经网络，将一个零部件的11项相似度信息输入到神经网络中，从而计算出与之最为相似的零部件，从而智能补全缺失数据。经过实验验证，本文所提出的缺失数据智能补全算法可以有效地利用已有的数据案例并填充缺失数据，极大地简化了生命周期评价过程中清单数据的收集工作，加快了机电产品LCA分析的速度。