BDS-2/BDS-3组合长基线三频RTK算法

蔡 巍，陈明剑，王 洋，邓 垦，施星宇，吕 葳

BDS-2/BDS-3组合长基线三频RTK算法

蔡 巍1,2，陈明剑1，王 洋2，邓 垦1，施星宇1，吕 葳1

（1. 信息工程大学 地理空间信息学院，郑州 450001；2. 西安测绘总站，西安 710054）

针对在长基线动态实时差分定位技术（RTK）中，由于整周模糊度容易受到大气延迟误差的影响，导致其固定率偏低，从而影响定位精度的问题，提出一种基于北斗卫星导航（区域）系统即北斗二号（BDS-2）和北斗三号全球卫星导航系统（BDS-3）组合的长基线定位方法：组合方法中BDS-2采用B1I、B2I和B3I 3种信号，BDS-3采用B1I、B2b和B3I 3种信号，充分利用三频中存在电离层延迟极小且具有整数特性的组合，同时考虑对流层延迟的影响，建立基于弱电离层组合的几何相关中长基线解算模型，并利用卡尔曼（Kalman）模型对天顶对流层延迟误差、三维坐标和弱电离层组合模糊度进行参数估计；再结合部分模糊度固定方法加快模糊度搜索效率，最终实现长基线RTK定位。实验结果表明，该方法能够在长基线下基本实现单历元模糊度固定，定位结果与流动站真值之间的定位偏差可达到厘米级。

动态实时差分定位技术（RTK）；北斗卫星导航系统（BDS）；三频观测值；整周模糊度；卡尔曼滤波；最小二乘模糊度降相关平差（LAMBDA）

0 引言

北斗卫星导航系统（BeiDou navigation satellite system，BDS）具有播发2个频率以上的观测值功能，将多个频率观测值进行组合得到具有波长较长、电离层影响较弱，以及低噪声等特性的组合观测值，可显著提高定位解算效率和模糊度固定率。往往在基线较长的条件下，大气延迟误差和观测噪声导致定位误差收敛速度变慢，整周模糊度求解变得困难，多频组合观测值的出现为卫星导航系统在长基线条件下的定位提供了更广阔的发展空间。

近几年研究者对利用BDS的多频组合观测值在中长基线条件下定位进行了大量的研究。李迪针对中长基线限制模糊度固定因素，提出先依次固定超宽巷和宽巷模糊度，然后利用模糊度固定后的组合观测值反算双差电离层延迟残差，将所得结果代入原始观测方程求解基础模糊度[1]。艾力·库尔班针对北斗三号全球卫星导航系统（BeiDou-3 global navigation satellite system，BDS-3）新的三频观测值，通过分析BDS-3三频线性组合观测值特性，选取高质量组合观测值，采用无几何无电离层模型（geometry-ionospheric-free，GIF）对实测BDS-3卫星数据进行超宽巷、宽巷和基础模糊度逐级固定[2]。但以上所提到的算法都是基于传统的三频模糊度算法（three carrier ambiguity resolution，TCAR）[3-5]，四舍五入固定各级模糊度；而由于观测噪声的影响，导致模糊度直接取整固定成功率较低，影响了定位精度[6-8]。张海平针对BDS中长基线实时动态定位，提出了以组合观测值的双差模糊度作为状态向量进行卡尔曼滤波的算法，并采用最小二乘模糊度降相关平差（least-squares ambiguity decorrelation adjustment，LAMBDA）方法搜索固定模糊度，对35～65 km基线数据的测试结果表明，模糊度单历元固定率达99.2%以上，定位精度达到厘米级[9]。随着基线长度的增加，大气延迟误差之间的空间相关性降低，导致全模糊度难以固定；如果采用北斗卫星导航（区域）系统即北斗二号（BeiDou navigation satellite (regional) system，BDS-2）/BDS-3组合定位和部分模糊度固定方法，模糊度固定率和定位精度将进一步提高。

针对上述问题，本文提出采用BDS-2/BDS-3系统组合进行定位，首先利用BDS三频线性组合的特性，选取最佳线性组合，采用无几何模型（geometry-free，GF）单历元解算超宽巷模糊度，再将超宽巷模糊度已固定的超宽巷组合联立伪距和窄巷组合，利用卡尔曼滤波和部分模糊度固定方法进行定位解算。

1 BDS三频线性组合

1.1 组合观测量

对BDS三频观测值进行线性组合，组合后的频率、波长和模糊度为

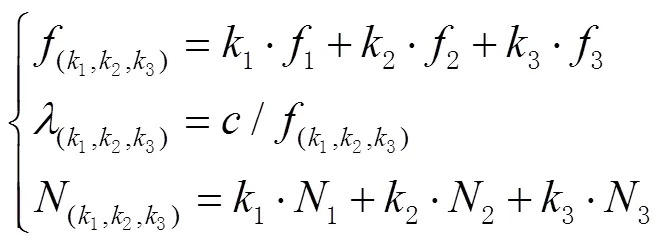
以“米”为单位的组合后的载波相位观测值可以表示为：

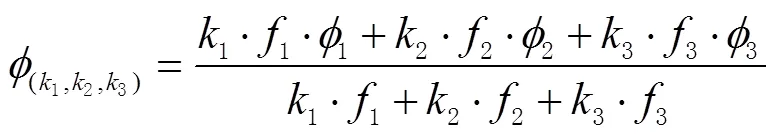
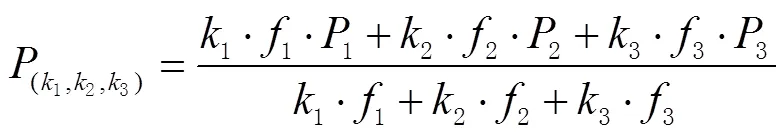
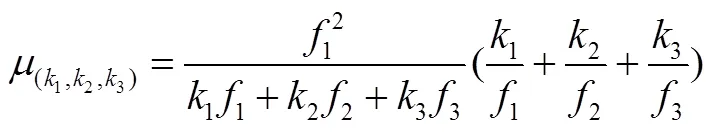
由式（4）减去式（5），可以得到多频无几何观测方程，即有

利用该方程可解算超宽巷模糊度。

1.2 BDS三频常用组合

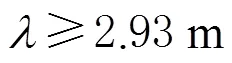
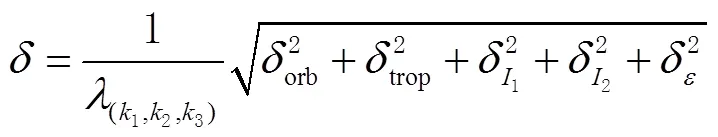
表1 BDS三频高质量超宽巷组合 m

顾及（1, －4, 3）组合观测噪声放大因子和电离层延迟系数较大的影响，超宽巷组合选取（0, 1, －1）和（1, －5, 4）2个组合。综合考虑BDS-2和BDS-3窄巷组合系数特性，窄巷组合中（3, 0, －2）的组合观测噪声放大因子和电离层延迟系数均较小，因此被选为最优窄巷组合。

2 BDS-2/BDS-3组合中长基线相对定位算法

2.1 基于GF模型单历元固定超宽巷模糊度

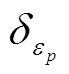
表2 最优超宽巷与不同伪距组合的GF组合 m

通过表2可以看出，伪距组合（1, 1, 1）与 2个最优超宽巷组合的GF组合精度最高，其组合观测精度约为0.1周，远远小于0.5周；理论上利用GF组合模型求出的超宽巷模糊度通过四舍五入直接取整就可以进行单历元固定。在超宽巷组合观测值波长和精度已知的情况下，利用式（9）从正态分布的表中可查到成功率，其公式为

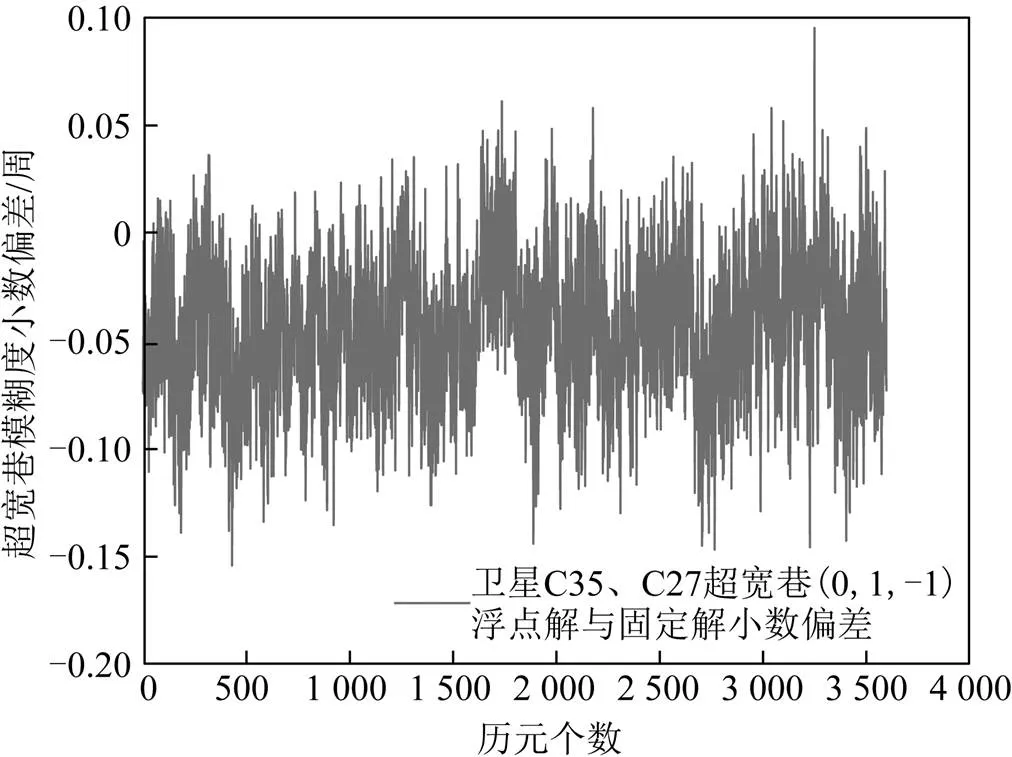
图1 卫星C35、C27超宽巷（0,1,-1）每个历元浮点解与固定解的偏差结果

图2 卫星C35、C27超宽巷（1,-5,4）每个历元浮点解与固定解的偏差结果

通过图1、图2可知，以卫星C35、C272组为例，超宽巷（0, 1, －1）和（1, －5, 4）每个历元浮点解与固定解的偏差值均远远小于±0.5周，可直接采用四舍五入单历元取整的方法固定超宽巷模糊度。

2.2 基于模糊度固定的超宽巷观测值卡尔曼滤波模型

将模糊度固定的超宽巷组合观测值和3个频率信号的伪距双差值作为约束条件，通过卡尔曼滤波（Kalman filter）固定弱电离层组合模糊度，以弱电离层组合模糊度、位置参数和相对天顶对流层延迟误差参数为状态向量进行实时卡尔曼滤波。

卡尔曼滤波的状态及量测方程的表达式为

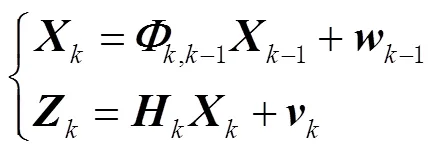
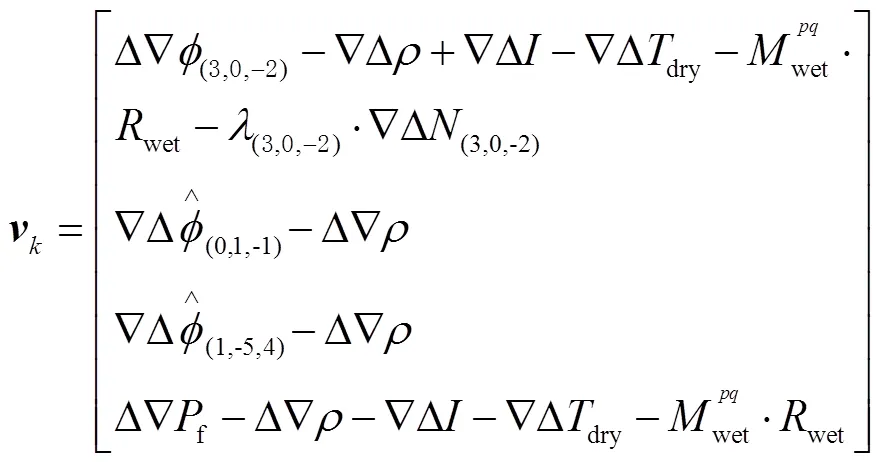
状态向量表达式为

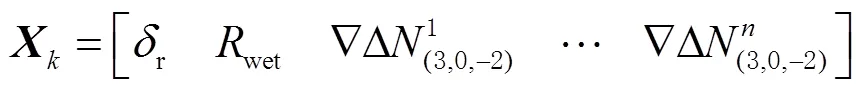
每个历元通过卡尔曼滤波得到坐标参数和模糊度的浮点解，之后利用部分模糊度固定算法得到弱电离层组合模糊度的固定解，将其回代到弱电离层组合观测方程中即可算出坐标参数的固定解[11]。

2.3 部分模糊度固定算法

部分模糊度固定算法主要分为以下几个步骤：

1）将卡尔曼滤波后得到的模糊度浮点解和方差-协方差阵输入到LAMBDA算法中去，首先按照预先设定的高度角剔除不满足条件的非参考星，经过LAMBDA算法得到模糊度新的方差并按从小到大的顺序排列。

2）利用自助法（bootstrapping）计算模糊度成功率[19-21]，如果大于成功率阀门值和满足条件的模糊度个数大于等于设置的最少卫星数，则进入比率（Ratio）值检测阶段，否则当前历元模糊度为浮点解。一般成功率阀门值设定为0.999，最少卫星数为5颗。

3）经过成功率检测后的模糊度还需要经过LAMBDA算法搜索和固定整数模糊度，主要方法是Ratio值检测（搜索后得到的整数解中次小与最小验后方差相除，如果比值大于Ratio阀门值3，则得到整周模糊度固定解），如果检测不通过则循环剔除最大方差模糊度，进入步骤2）。

3 实验与结果分析

为验证上述模型的可行性，本文采用河南省内的3组基线数据进行验证。1）基线1。观测日期为2022年7月8日（1 h），基线长度为74.9 km，采样间隔为1 s。解算过程中，设定卫星截止高度角为20°。2）基线2。观测日期为2022年9月23日0:00—5:00（5 h），基线长度为134.1 km，采样间隔为1 s。解算过程中，设定卫星截止高度角为20°。3）基线3。观测日期为2022年9月23日0:00—5:00（5 h），基线长度为84.4 km，采样间隔为1 s。解算过程中，设定卫星截止高度角为20°。3条基线均采用的3种频率分别为BDS-2的B1I、B2I、B3I，BDS-3的B1I、B2b、B3I，模糊度固定方式采用连续静态整数模糊度估计和解算模式（fix and hold），Ratio阀值采用3.0。同时采用相同的数据处理方式对BDS-2信号进行处理，其结果作为比较对象。如图3、图4和图5分别为基线1～基线3的2个测站之间有效共视卫星数、窄巷组合定位结果与真值之间的偏差与部分模糊度固定方法的Ratio变化情况，图中E表示东、N表示北，U表示天顶。从图中可以看出基线1～基线3的2个测站之间满足解算条件的BDS共视卫星数量，所有历元卫星可视数量均在15颗以上，相对于单系统卫星数，BDS-2/BDS-3组合卫星数量更多，其定位性能更优越。

图3 基线1 BDS的共视卫星数/窄巷定位偏差/窄巷模糊度Ratio变化

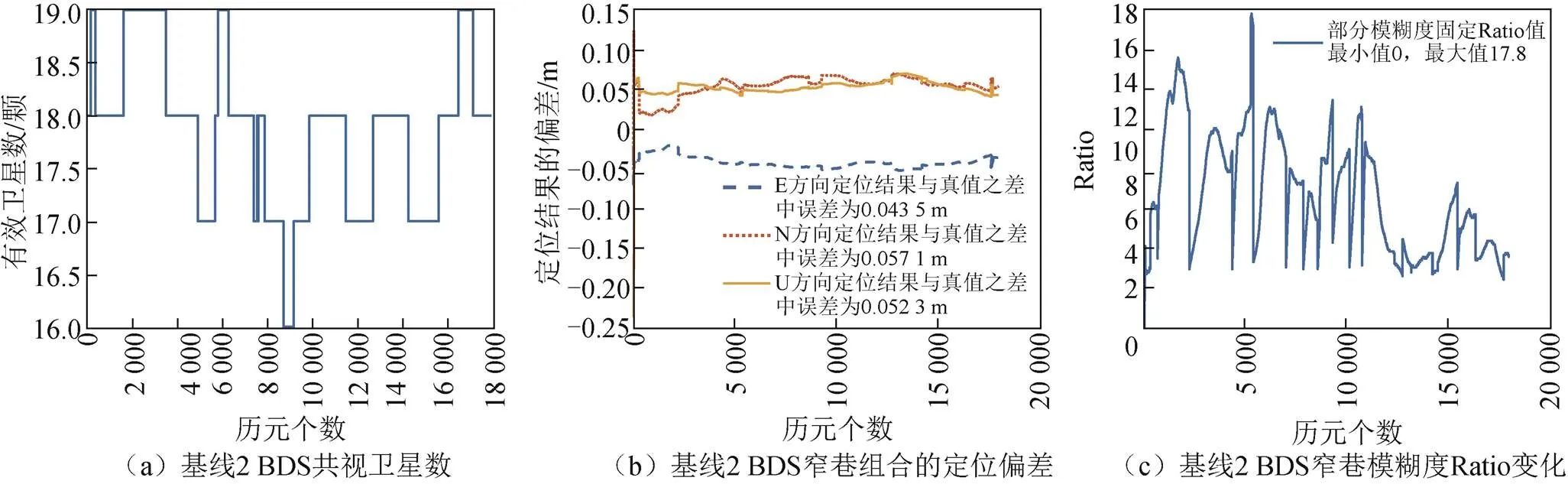
图4 基线2 BDS的共视卫星数/窄巷定位偏差/窄巷模糊度Ratio变化

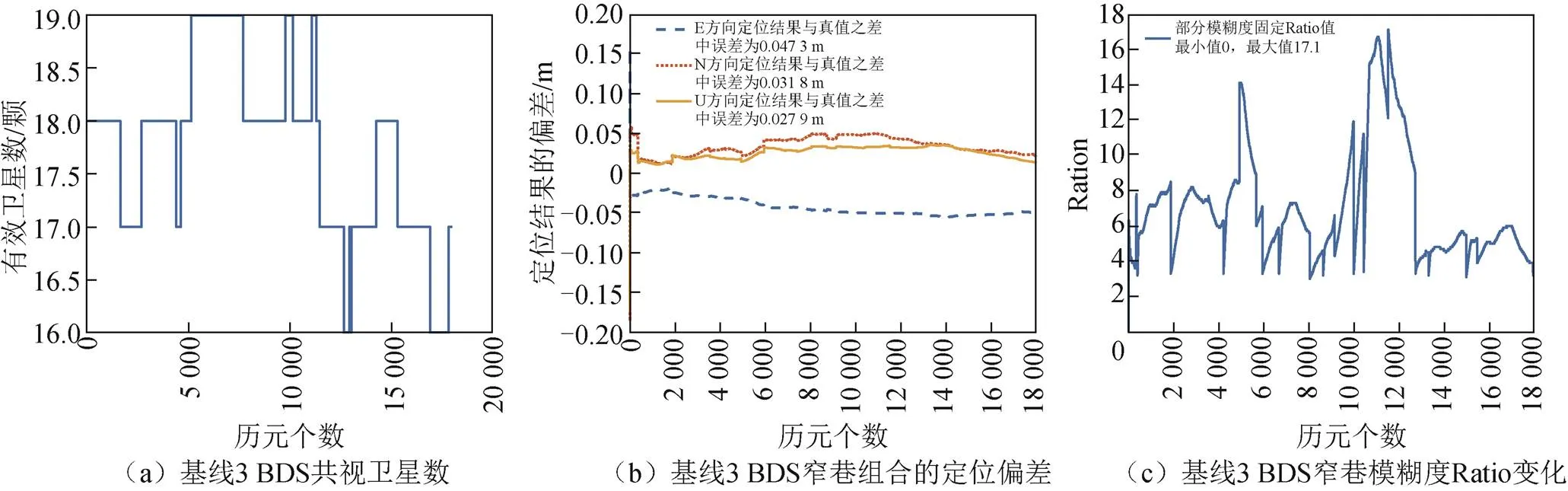
图5 基线3 BDS的共视卫星数/窄巷定位偏差/窄巷模糊度Ratio变化

从图3～图5可以看出，3条基线采用BDS基于弱电离层组合的几何相关（geometry-based）中长基线解算模型，E、N和U 3个方向的定位结果偏差均为厘米级。如图6所示为采用相同的方法处理单系统BDS-2数据，E、N和U 3个方向的定位结果偏差均大于组合系统的偏差值，其模糊度初始化时间均比组合系统的初始化时间长，并且BDS-2有效的共视卫星数大部分维持在9颗，卫星数量少于组合系统的卫星数，从而导致参与解算的数据要少于组合系统。这些原因均导致定位结果偏差增大和模糊度搜索效率降低。BDS/BDS-2的具体定位结果如表3所示，模糊度初始化时间（以历元个数计）如表4所示。

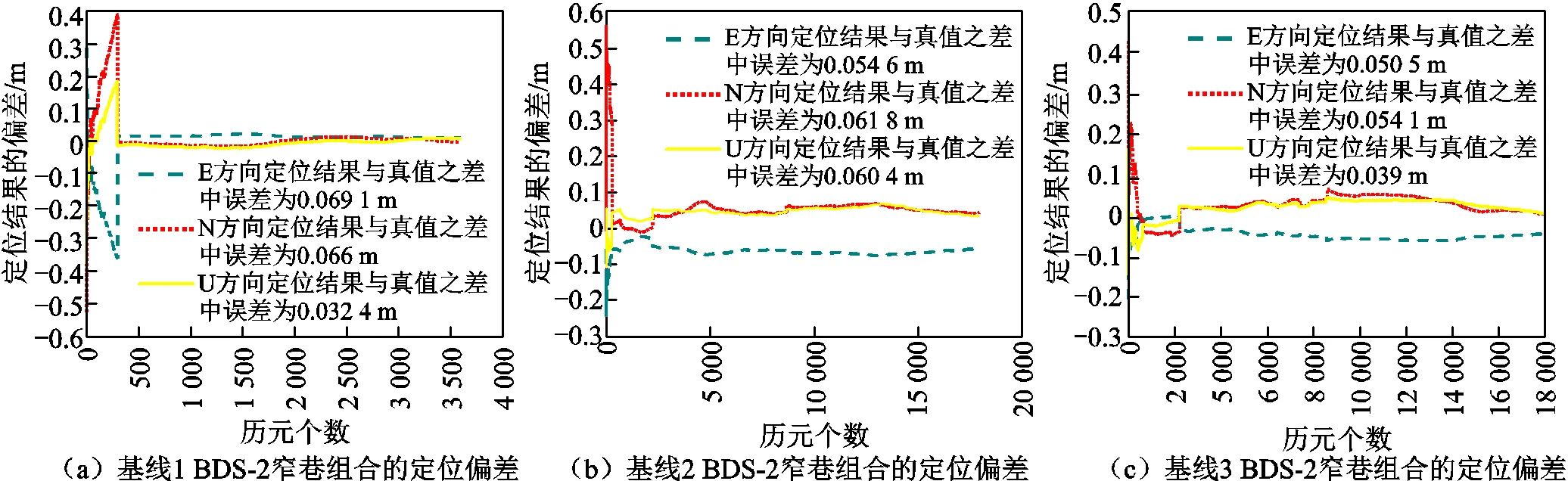
图6 基线1/基线2/基线3 BDS-2窄巷组合的定位偏差

表3 BDS/BDS-2的3条基线定位结果偏差统计 m

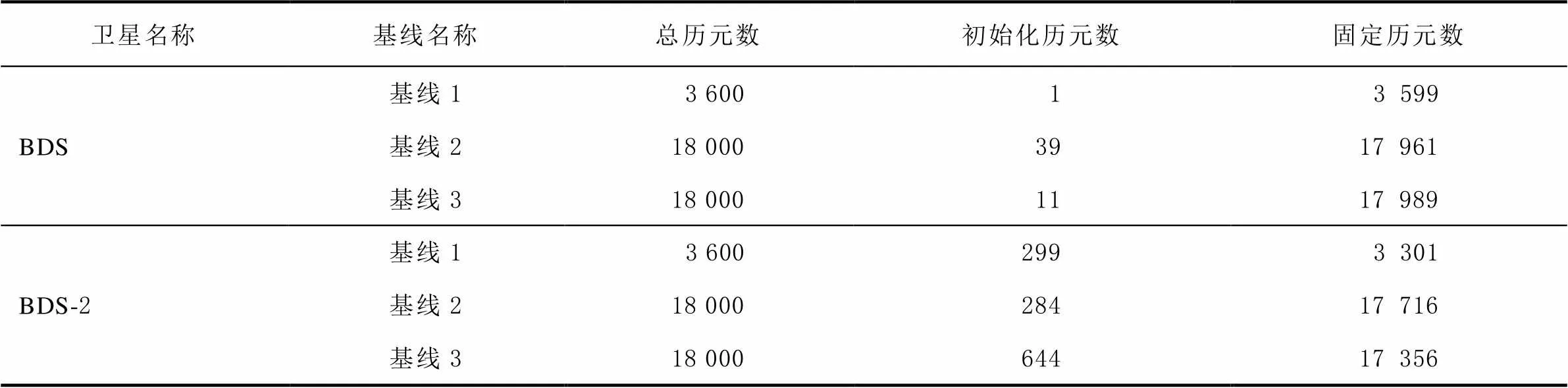
表4 BDS/BDS-2模糊度初始化时间 s

4 结束语

本文基于74.9、134.1和84.4 km的3组中长基线数据，利用BDS-2/BDS-3的B1I、B2I/B2b、B3I 3种频率进行线性组合，通过基于弱电离层组合的Geometry-based中长基线解算模型结合卡尔曼滤波和LAMBDA算法实时定位解算。经过实验解算结果分析，得出该方法可以在中长基线下基本实现单历元模糊度固定，定位偏差达到厘米级高精度相对定位标准，精度要高于单BDS-2系统。由于基线的距离导致大气延迟之间的相关性降低，因而难以实现全模糊度固定，通过部分模糊度固定方法可以有效提高模糊度固定率。基线1～基线3中长基线下，固定历元数与总的历元数相比，模糊度固定率均达到99%以上。部分模糊度固定方法具有明显的优势，在保证整周模糊度固定可靠性的同时，可以提高定位的精度、稳定性和可靠性。

综上所述，BDS-2/BDS-3组合三频在中长基线的条件下定位性能较优，可为今后的中长基线快速高精度定位提供参考。

[1] 李迪.北斗三频模糊度固定算法研究[D].郑州:信息工程大学,2017.

[2] 艾力·库尔班,章浙涛,何秀凤.北斗三号新三频相位模糊度固定方法[J].测绘科学技术学报,2021,38(1):21-27,32.

[3] 刘炎炎,叶世榕,江鹏,等.基于北斗三频的短基线单历元模糊度固定[J].武汉大学学报(信息科学版),2015,40(2):209-213.

[4] FENG Y, RIZOS C. Geometry-Based TCAR models and performance analysis[J]. Observing Our Changing Earth, 2009, 133: 645-653.

[5] 于文浩,张云,韩彦岭,等.北斗三频中长基线差分定位性能研究[J].全球定位系统,2018,43(4):102-109.

[6] 金俭俭.多频多系统GNSS中长基线解算技术及其应用开发研究[D].南京:东南大学,2020.

[7] LIU L, PAN S, GAO W, et al. Assessment of quad-frequency long-baseline positioning with BeiDou-3 and Galileo observations. [J]. Remote Sensing, 2021, 13(8): 1551.

[8] ZHANG R, GAO C, WANG Z, et al. Ambiguity resolution for long baseline in a network with BDS-3 quad-frequency ionosphere-weighted model[J]. Remote Sensing, 2022, 14(7): 1654.

[9] 张海平.北斗三号中长基线RTK卡尔曼滤波算法[J].测绘科学,2020,45(12):28-33,61.

[10] 许扬胤.北斗动对动高精度相对定位技术研究[D].郑州:信息工程大学,2017.

[11] 李毓照. 多频GNSS单历元模糊度解算方法[D].兰州:兰州交通大学,2022.

[12] 张浙涛,李博峰,何秀凤,等.北斗三号多频相位模糊度无几何单历元固定方法[J].测绘学报,2020,49(9):1139-1148.

[13] YAO Y, ZHANG X, CAO X, et al. An efficient cycle-slip repair model with high success rate for BDS triple- frequency observations[J]. IEEE Access, 2019, 7: 142750-142761.

[14] ZHANG Z, LI B, HE X, et al. Models, methods and assessment of four-frequency carrier ambiguity resolution for BeiDou-3 observations[J]. GPS Solutions, 2020, 24(4): 96.

[15] 李毓照, 杨维芳, 闫浩文, 等. BDS-3多频信号最优线性组合及特性分析[J]. 大地测量与地球动力学, 2022, 42(6): 612-615.

[16] 吕震, 王振杰, 刘金萍, 等. 顾及电离层延迟的BDS-3四频长基线定位算法[J]. 测绘通报, 2023(4): 71-78.

[17] 高猛,徐爱功,祝会忠,等.BDS网络RTK参考站三频整周模糊度解算方法[J].测绘学报,2017,46(4):442-452.

[18] 高猛, 王顺顺, 王操, 等. BDS中长基线三频RTK算法研究[J]. 大地测量与地球动力学, 2022, 42(1): 5-8, 20.

[19] 王建敏,马天明,祝会忠.BDS/GPS整周模糊度实时快速解算[J].中国矿业大学学报,2017,46(3):672-678.

[20] 金俭俭, 高成发, 张瑞成, 等. GPS与BDS-2、BDS-3融合数据短基线解算精度分析[J]. 测绘通报, 2020(3): 83-86,95.

[21] 储超. 基于部分模糊度固定的RTK/INS紧组合算法研究[D].武汉: 武汉大学, 2020.

Algorithm of three-frequency RTK at long baseline for BDS-2/BDS-3 combination

CAI Wei1,2, CHEN Mingjian1, WANG Yang2, DENG Ken1, SHI Xingyu1, LYU Wei1

（1. Institute of Geospatial Information, Information Engineering University, Zhengzhou 450001, China; 2. Xi′an Mapping Terminus, Xi′an 710054, China）

Aiming at the problem that because it is susceptible to atmospheric delay error for the integer ambiguity, the fixed rate is low, which affects the positioning accuracy, the paper proposed a long baseline positioning method based on the combination of BeiDou navigation satellite (regional) system (BDS-2) and BeiDou-3 global navigation satellite system (BDS-3): in the combination method, BDS-2 adopted B1I, B2I and B3I signals, while BDS-3 adopted B1I, B2b and B3I signals, making full use of the combination with minimal ionospheric delay and integer characteristics in the three-frequency; at the same time, considering the influence of tropospheric delay, a geometry-based middle-long baseline solution model based on weak ionospheric combination was established, and Kalman model was used to estimate the parameters of zenith tropospheric delay error, three-dimensional coordinates and fuzzy degree of weak ionosphere combination; then combined with partial ambiguity fixed method,the efficiency of ambiguity search was accelerated; finally, the long-baseline RTK positioning was realized. Experimental result showed that the proposed method could basically achieve the fixed ambiguity of single epoch under long baseline, and the positioning deviation between the positioning result and the true value of the rover station could be up to centimeter level.

real-time kinematic (RTK); BeiDou navigation satellite system (BDS); three-frequency observations; integer ambiguity; Kalman filter; least-squares ambiguity decorrelation adjustment (LAMBDA)

蔡巍，陈明剑，王洋, 等. BDS-2/BDS-3组合长基线三频RTK算法[J]. 导航定位学报, 2023, 11(6): 142-149.（CAI Wei, CHEN Mingjian, WANG Yang, et al. Algorithm of three-frequency RTK at long baseline for BDS-2/BDS-3 combination[J]. Journal of Navigation and Positioning, 2023, 11(6): 142-149.）DOI:10.16547/j.cnki.10-1096.20230617.

P228

A

2095-4999(2023)06-0142-08

2023-11-23

蔡巍（1987—），男，湖北宜昌人，硕士，工程师，研究方向为卫星导航与定位。