顾及气候类型的区域加权平均温度模型

刘金涛，吕伟才，肖星星，卢福康

顾及气候类型的区域加权平均温度模型

刘金涛，吕伟才，肖星星，卢福康

（安徽理工大学 空间信息与测绘工程学院/矿区环境与灾害协同监测煤炭行业工程研究中心/矿山采动灾害空天地协同监测与预警安徽普通高校重点实验室，安徽 淮南 232001）

针对由于中国土地面积广阔，气候类型复杂，大气加权平均温度（m）易受气候类型、纬度和海拔影响的问题，提出一种顾及气候类型的区域加权平均温度模型：根据中国区域内分布广泛的5种气候类型，利用中国境内73个探空站2007—2015年的探空数据，分区域建立顾及气候类型及地面气温（s）、饱和水汽压（s）的大气加权平均温度模型ET-TM模型；并用2016年的探空数据结合贝维斯（Bevis）模型和GPT-3模型共同验证ET-TM模型的精度。结果表明：ET-TM模型整体精度高于Bevis模型和GPT-3模型；分区域建立大气加权平均温度模型有利于减少纬度和高程对大气加权平均温度的影响；对比Bevis模型和GPT-3模型，ET-TM模型更适用于中国区域内的大气可降水量反演。

大气可降水量（PWV）；大气加权平均温度（m）；气候类型；水汽反演；残差拟合

0 引言

全球卫星导航系统（global navigation satellite system，GNSS）是20世纪对人类影响最大的空间信息技术。近年来，利用GNSS导航卫星进行水汽反演有了巨大的进步[1]。大气加权平均温度（atmosphericweighted mean temperature，m）是湿延迟向大气可降水量（precipitable water vapor，PWV）转换的重要参数，其m精度的高低将直接影响到GNSS水汽反演的精度[2-3]。目前常用的m计算方法主要有2种[4]：一种是利用探空站的水汽压和气温数据积分得到，该方法精度较高[5]；另一种是利用经验模型计算，如全球压力和温度模型（global pressure and temperature model，GPT）GPT-2模型[6]、GPT-3模型[7]等。

文献[8]首次提出了m的概念，并认为北美地区的m和地面气温（s）具有很强的相关性。该模型是基于美国探空站建立的适合中纬度地区的模型；但由于对流层的区域不确定性，该模型应用于其他地区势必会产生较大的偏差。此后，诸多学者开始分析研究局地m变化规律。文献[9]利用2015—2018年的探空数据建立了顾及s、饱和水汽压（s）、海拔、纬度及残差的BET模型，其精度优于贝维斯（Bevis）模型、GPT3w-1模型和GPT3w-5模型。该模型的偏差（ias）和均方根误差（ms）抗高程和纬度的能力优于上述3种模型。文献[10]利用2007—2014年的全球大地测量观测系统（global geodetic observing system，GGOS）数据建立了一种顾及季节变化以及垂直递减率的CTm格网模型，且该模型无需气象因子的输入。相较于GPT2w模型，该模型在我国地区表现出良好的精度和稳定性。文献[11]利用2014—2016年的探空数据，在Bevis模型的基础上加入了高程和季节变化，建立了中国西部地区的新m模型，其在中国西部地区表现出了良好的适用性，受到高程和四季变化的影响较小。文献[12]利用2015—2017年的中国南部地区的探空数据分别建立了顾及s的m-SC1模型以及顾及s、高程、季节变化和纬度的m-SC2模型，在中国南部地区未表现出明显的季节性变化，在空间域上有更好的适用性，有效提高了中国南部地区的GNSS水汽反演精度。因此利用长时间序列的气象资料建立了局地m模型，在提升局地GNSS-PWV反演方面有着重要意义。

中国土地面积广阔，气候类型复杂，地势整体表现为西高东低，依据气候类型进行m建模不仅仅可以降低气候对m的影响，还可相应地降低纬度和海拔对m的影响。因此本文顾及气候类型对m的影响，构建多因子m模型，并对其进行精度评定。

1 数据来源及原理

选择中国境内的73个探空站（如图1所示），从2007—2016共10 a的探空数据，采样时间分别为协调世界时（universal time coordinated，UTC）的0点和12点，探空数据来自美国怀俄明大学。为证明探空数据的完整性，从73个探空站点中随机选取8个站点计算其数据完整性，结果如表1所示。

图1 中国部分探空站点分布

表1 部分站点每年的数据完整率 %

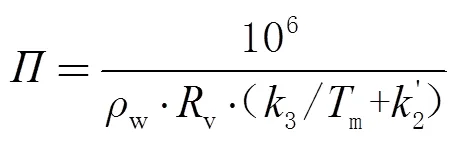
2 大气加权温度（Tm）模型的建立

2.1 相关性分析

中国陆地面积广袤，地形气候复杂，影响m的因素较多。研究表明，大气加权平均温度与地面气温[14]和水汽压[15-16]均具有一定的相关性。选取全国73个探空站利用积分法计算出相应的m。以北京探空站为例，探究m与s、s之间的相关性（如图2所示）。

图2 Tm与Ts、Es相关性分析

从图2中可以看出：m与s之间具有线性关系，且随着s的增加，m也随之增加，二者呈正相关关系，相关系数为0.838，相关性较高；m与s存在幂关系，相关系数为0.855。因此在m建模的过程中，在Bevis模型的基础上考虑了s因素。

2.2 Tm模型的建立

热带季风气候、亚热带季风气候、温带季风气候、温带大陆性气候和高山高原气候是我国主要的5种气候类型。按照各探空站所属的气候类型，将73个探空站进行分类[17]，分类结果如表2所示。利用2007—2015年共9 a的探空数据进行建模，并用2016年的探空数据验证所建立模型的精度。

表2 各气候区域内探空站数量

利用73个探空站9 a的数据，采用多元非线性拟合的方法，建立s、s-m多因子的大气加权温度模型。

设m函数方程为

式中、、、为待拟合参数。

拟合出的m模型如表3所示。

表3 各气候区域内的多因子Tm模型

（续）

由表3可知，5种气候区域的m模型中，m-s、s模型计算的m与探空站积分计算的m相关系数均在0.8以上，拟合效果较好，其中温带季风气候区域内m模型相关系数达到了0.92。

2.3 残差分析

研究表明，实测获取的m与m模型之间的残差具有一定周期性[18]，因此提升m模型的精度不能只考虑气象因素，还应当考虑到s、s-m模型随时间的变化关系[19]。如图3所示，利用快速傅里叶变换（fast Fourier transform，FFT）分析m的周期特性，其能量级数的峰值出现在181和362 d附近。

本文使用具有年周期、半年周期的三角函数来拟合s、s-m模型产生的残差，将三角函数的值视为季节性修正，避免了计算不同季节的模型参数，并将最终的模型命名为ET-TM模型。

图3 探空站点时间序列残差与FFT下的周期特性

设m残差模型为

式中：oy为年积日；(1)为残差年均值；(2)、(3)为年周期系数；(4)、(5)为半年周期系数。

具体结果如表4所示。

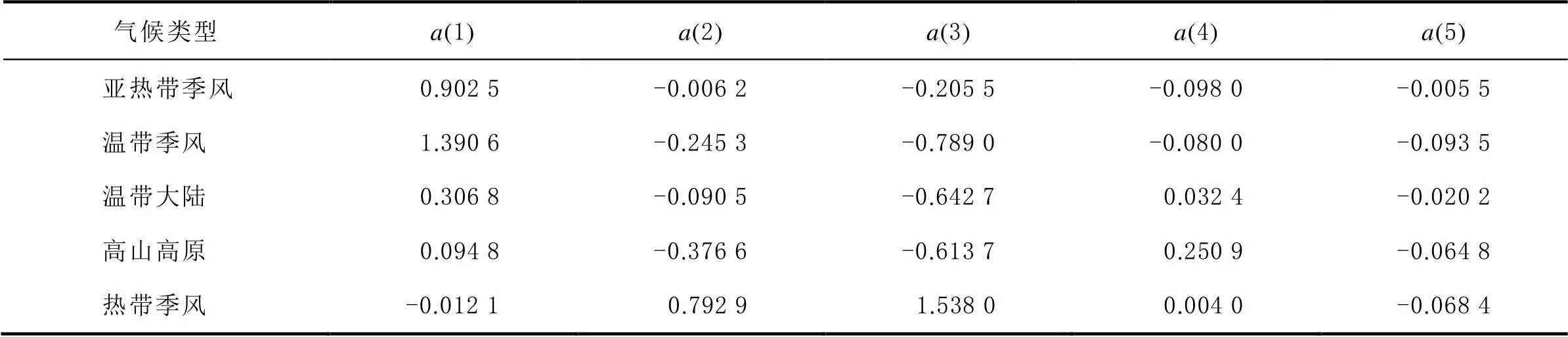
表4 各气候类型下的Tm残差模型系数

最终m模型为

式中m0为s、s-m模型。在利用该模型计算m时，只须输入s、s和oy，即可得到相应的大气加权平均温度。

3 实验与结果分析

为验证该模型计算m的精度，将2016年的探空数据积分得到的m作为真实值，验证该模型的精度。利用平均偏差ias和均方根误差ms作为精度评价指标，有：

3.1 基于探空数据的模型精度分析

利用73个探空站2016年的探空数据来验证ET-TM模型的精度，并结合Bevis模型和GPT-3模型进行对比，综合分析ET-TM模型计算m的性能，并计算各个模型的ias和ms。具体结果如表5所示。

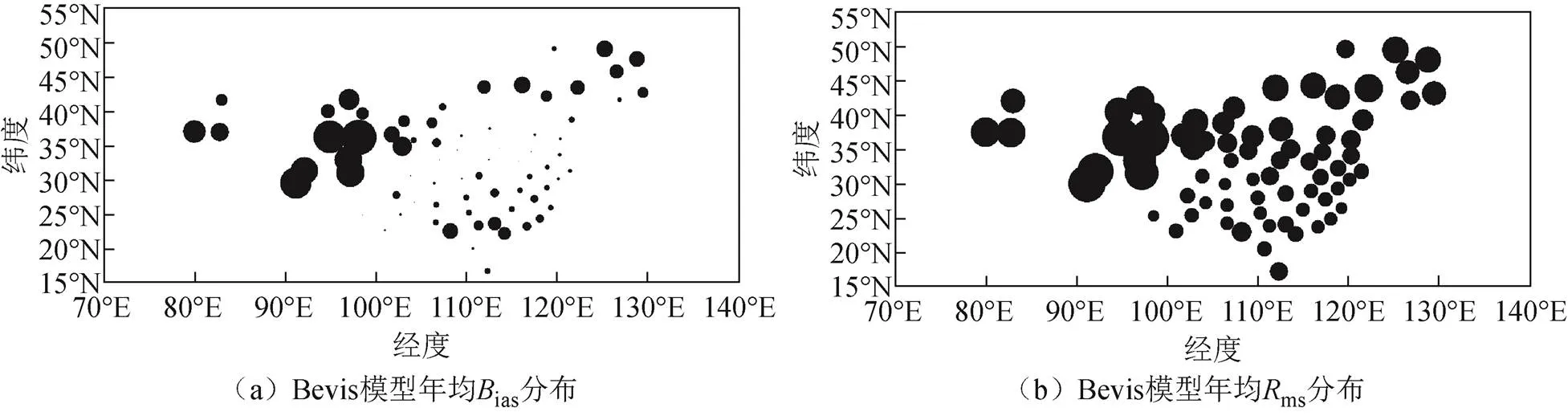
由表5可知：除热带季风气候区和亚热带季风气候区外，Bevis模型年均ias均表现为负偏差，其年均ias分别为1.28、－1.26、－2.32、－5.64、1.22 K；GPT-3模型在5种气候区域内均表现为正偏差，年平均偏差分别为0.90、0.38、1.54、3.65、0.20 K。因此，Bevis模型和GPT-3模型计算的m在中国区域内存在一定的系统误差，同时Bevis模型和GPT-3模型在高海拔地区的高山高原气候区偏差最大。ET-TM模型在中国5种气候区域的偏差最小为－2.16 K，最大为2.19 K，年平均偏差分别为－0.04、0.03、0.11、0.13、0.35 K，波动较小。Bevis模型的ms在5种气候区域内分别为3.12、4.32、4.81、6.80、2.98 K；GPT-3模型在5种气候区域内的ms分别为3.82、4.77、4.99、5.07、2.70 K；ET-TM模型的ms分别为2.67、3.33、3.44、2.68、2.26 K，相对于Bevis模型分别提高了0.45 K(14.4%)、0.99 K(22.9%)、1.37 K(28.5%)、4.12 K(60.6%)、0.72 K（24.16%），相对于GPT-3分别提高了1.15 K (30.1%)、1.44 K(30.2%)、1.55 K(30.1%)、2.39 K (47.1%)、0.44 K（16.30%）。由此可以说明，ET-TM模型在中国5种气候区域内的精度均优于Bevis模型和GPT-3模型，且涵盖因素更多、偏差更小。如图4所示为Bevis模型、GPT-3模型、ET-TM模型的年均ias、ms分布情况，图中黑点的面积代表其数值大小。

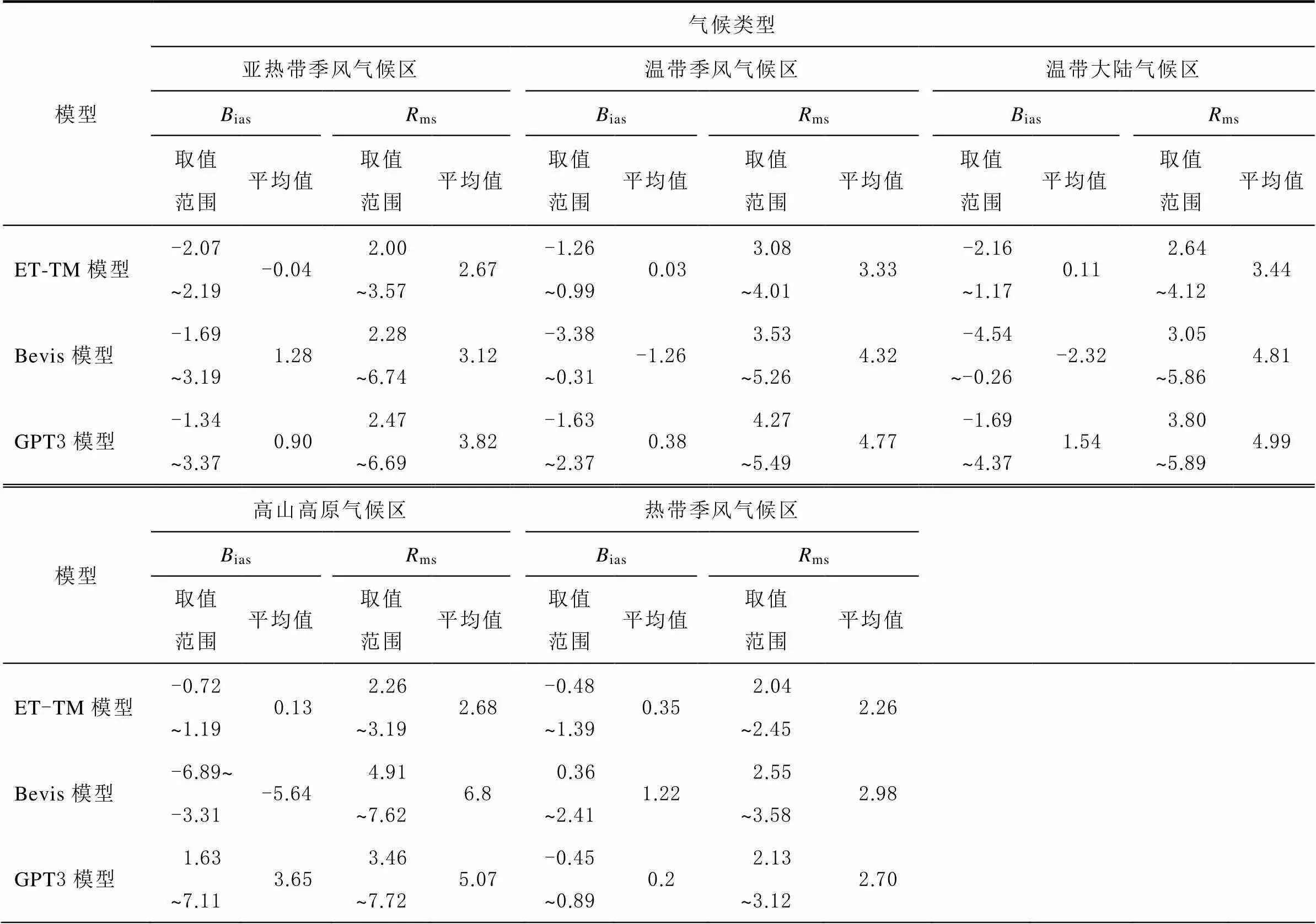
表5 4种气候区域内3种模型精度对比 K

由图4可知：在热带季风区域，虽然探空站点较少，但仍能看出ET-TM模型要优于Bevis模型和GPT-3模型；Bevis模型在亚热带季风区域和温带季风区域的南部适用性较好，年均ias在5种气候区域内较小，在海拔较高的高山高原气候区域内系统误差最大，同时在温带季风气候区的北部年均ias较大，由此可见Bevis模型易受到海拔和纬度的影响；GPT-3模型在亚热带季风、温带季风气候区域内年均ias较小，在高山高原气候区域内偏差较大，同样受到纬度和海拔的影响，且海拔造成的影响明显大于纬度因素；ET-TM模型考虑到气候类型对m的影响，按照气候类型对中国区域进行m建模，这既减小了气候的影响，又减小了纬度和海拔2种因素的影响，其年均ias在3种模型中最小。从年均ms来看，Bevis模型为单因子模型，仅使用s进行了建模，在中国亚热带季风区域内年均ms较小，但在高海拔地区青藏高原区域，年均ms较大，最大为7.62 K，在温带季风区域北端，其年均偏差ms部分超过5 K；GPT-3模型在建模时考虑了残差的季节性变化，其年均ms整体小于Bevis模型，年均ms较大值也出现在高海拔和高纬度地区；ET-TM模型年均ms在3种模型中最小，与Bevis模型相比，最大优势在于青藏高原地区，ET-TM模型年均ms在青藏高原地区最大值为2.68 K，与GPT-3模型相比，ET-TM模型年均ms相对稳定，波动较小。总体来说，ET-TM模型要优于Bevis模型、GPT-3模型。

为了更好地检验ET-TM模型的精度及适用性，绘制热带季风气候、亚热带季风气候、温带季风气候、温带大陆气候和高山高原气候区域内的不同模型的日均ias和日均ms散点图并进行统计分析，结果如图5、图6所示。

由图5可以看出：ET-TM模型ias在5种气候类型区域内变化较为平缓，相对稳定，ias总体较小；Bevis模型和GPT-3模型在我国亚热带季风区域内适应性较高，但其在建模过程当中未顾及高程因素，造成在青藏高原等高海拔地区产生了较大的偏差。Bevis模型在温带季风、温带大陆和高山高原气候区内日均ias表现为春夏季节偏差小，秋冬季节偏差大的特点，存在一定的季节性变化，在3个气候区域内整体表现为负偏差，而在热带季风气候区域内，其偏差在春冬季节偏差较大，其他时间偏差相对较小；GPT-3和ET-TM模型均考虑了残差的季节性变化，因此GPT-3模型和ET-TM模型受季节的影响较小，二者日均ias变化趋势基本相同，但GPT-3模型计算得出的m整体上高于积分法计算的m，在5种气候区域内均表现为正偏差。

由图6可知：从ms角度来说，在亚热带季风区域内3种模型均未表现出明显的季节性变化，但在温带季风区域内，3种模型的日均ms在夏季偏小，其余时间段较大；在热带季风气候、温带大陆性气候和高山高原气候区域内，Bevis模型表现出一定的季节性差异，在热带季风气候区域和高山高原气候区域内较为明显，全年表现为夏季ms较小，春秋季节ms较大；GPT-3模型的日均ms在热带季风区域和温带季风区域显示出一定的季节性变化，在其他3个区域均未出现明显的季节性变化，但GPT-3模型的日均ms波动较大且不稳定；ET-TM模型日均ms均小于Bevis模型和GPT-3模型，波动范围小，相对稳定。综合图5和图6可知：从亚热带季风气候到温带季风区域，随着纬度的增加，Bevis模型和GPT-3模型的ias和ms逐渐增大；同时，由亚热带季风到高山高原气候区，随着海拔的增加，Bevis模型和GPT-3模型的ias和ms也逐渐变大。由此可见，纬度和高程对m模型有着极大的影响，但海拔因素的影响要远大于纬度因素的影响。ET-TM模型虽未考虑高程和纬度因素的影响，但按照气候类型划分区域建模的方法总体上减小了高程和纬度的变化。因此ET-TM模型在全年当中受到季节性影响较小，全年相对平稳，同时受纬度和高程的影响也相对较小。

3.2 Tm对GNSS-PWV反演的精度分析

m模型构建的目的在于应用于GNSS-PWV反演，但在多数情况下，GNSS观测站与探空站并不共址，因此很难全面可靠地研究m模型对GNSS-PWV反演的影响。目前已有文献从理论上研究了m对GNSS-PWV反演的影响[20]，本文利用该方法评估ET-TM模型对GNSS-PWV反演的影响，即

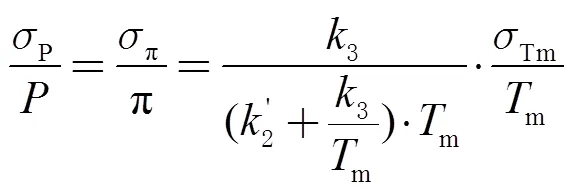
式中：p为大气可降水量PWV的ms；为该区域的大气可降水量PWV；π为水汽转换系数的ms；Tm为大气加权平均温度的年均ms。利用p/作为表征m对GNSS-PWV反演的影响。

如表6所示为3种模型计算PWV的理论ms和相对误差。

表6 ET-TM模型、Bevis模型和GPT-3模型计算PWV的理论Rms和相对误差 mm

（续）

依据表6可知，ET-TM模型的PWV在5种气候区域内的最大值、最小值分别为0.423、0.086 mm，小于Bevis模型和GPT-3模型，整体上优于Bevis模型和GPT-3模型；从PWV/的结果来看，ET-TM模型在5个区域内的平均值分别为0.009、0.012、0.013、0.01、0.008 mm，相比于Bevis模型和GPT3模型波动更小，展现了ET-TM模型的稳定性。因此该模型可以为中国区域的GNSS-PWV反演提供高精度的m值。

4 结束语

1）本文利用2007—2015年共9 a的探空数据，采用回归分析方法，建立了适用于中国热带季风气候、亚热带季风气候、温带季风气候、温带大陆性气候和高山高原气候5种气候区域下的ET-TM模型；并使用2016年的数据对建立的模型进行了精度分析，得到5种气候类型下的年均ias和年均ms。

2）ET-TM模型考虑到气候因素，同时利用与m相关性较高的s和s2个因子对m进行建模，并对残差序列进行分析。利用该方法进行建模，不仅减小了气候条件和季节的影响，还在一定程度上减少了纬度和海拔2种因素的影响。

3）通过对PWV、PWV/的分析，ET-TM模型的PWV在5种气候区域内最大为0.325 mm，最小为0.086 mm，PWV/在5种气候区域内最大为0.013，最小为0.008，均优于Bevis模型和GPT-3模型。

总体来看，ET-TM模型计算的m精度更高且更可靠，可以更好地满足中国区域内的GNSS-PWV反演需要，更好地服务于中国GNSS气象学的研究工作。

[1] 姚欢欢, 党亚民, 许长辉, 等. 不同气候类型北斗反演大气可降水量性能分析[J]. 测绘科学, 2022, 47(10): 21-28.

[2] 黄良珂, 吴丕团, 王浩宇, 等. 中国西南地区GPS大气水汽转换系数模型精化研究[J]. 大地测量与地球动力学, 2019, 39(3): 256-261.

[3] 侯晓玲, 熊永良. 川渝地区大气加权平均温度模型优化[J]. 导航定位学报, 2023, 11(4): 63-69.

[4] 谢劭峰, 张继洪, 王义杰, 等. 大气加权平均温度垂直递减率时空特性分析[J]. 大地测量与地球动力学, 2023, 43(6): 593-599.

[5] 郑磊. 顾及季节变化的西南地区大气加权平均温度模型[J]. 导航定位学报, 2021, 9(4): 98-103.

[6] LAGLER K, SCHINDELEGGER M, BÖHM J, et al. Gpt2: Empirical slant delay model for radio space geodetic techniques[J]. Geophysical Research Letters, 2013, 40(6): 1069-1073.

[7] Landskron Daniel, Bohm Johannes. Vmf3/gpt3: Refined discrete and empirical troposphere mapping functions[J]. Journal of Geodesy, 2018, 92(4): 349-360.

[8] BEVIS M, BUSINGER S, HERRING T A, et al. GPS meteorology: Mapping zenith wet delays onto precipitable water[J]. Journal of Applied Meteorology, 1994, 33(3): 379-386.

[9] 李浩杰, 刘立龙, 黄良珂, 等. 顾及多因子影响的中国区域T_m模型精化研究[J]. 大地测量与地球动力学, 2022, 42(4): 393-397.

[10] 黄良珂, 彭华, 刘立龙, 等. 顾及垂直递减率函数的中国区域大气加权平均温度模型[J]. 测绘学报, 2020, 49(4): 432-442.

[11] 莫智翔, 黎杏, 黄良珂, 等. 顾及多因子影响的中国西部地区大气加权平均温度模型精化研究[J]. 大地测量与地球动力学, 2021, 41(2): 145-151.

[12] 廖发圣, 黄良珂, 刘立龙, 等. 中国南部地区大气加权平均温度模型精化研究[J]. 大地测量与地球动力学, 2022, 42(1): 41-47.

[13] 罗宇, 罗林艳, 吕冠儒. 加权平均温度模型对GPS水汽反演的影响[J]. 测绘科学, 2018, 43(9): 6-9, 15.

[14] Ding M. A neural network model for predicting weighted mean temperature[J]. Journal of Geodesy, 2018, 92(10): 1187-1198.

[15] 王皓, 赵兴旺. 香港地区大气加权平均温度建模与研究[J]. 全球定位系统, 2019, 44(1): 119-124.

[16] 王瀚弘, 魏冠军, 张幸, 等. 兰州地区区域加权平均温度模型构建方法研究[J]. 导航定位学报, 2022, 10(1): 90-96, 129.

[17] 中华人民共和国气候图集编委会. 中华人民共和国气候图集[M]. 第1版. 北京: 气象出版社, 2002.

[18] Yao Y, Zhang B, Xu C, et al. Improved one/multi-parameter models that consider seasonal and geographic variations for estimating weighted mean temperature in ground-based gps meteorology[J]. Journal of Geodesy, 2014, 88(3): 273-282.

[19] 张迪, 袁林果, 黄良珂, 等. 澳大利亚区域大气加权平均温度建模[J]. 武汉大学学报（信息科学版）, 2022, 47(7): 1146-1153.

[20] Huang Liangke, Jiang Weiping, Liu Lilong, et al. A new global grid model for the determination of atmospheric weighted mean temperature in gps precipitable water vapor[J]. Journal of Geodesy, 2019, 93(2): 159-176.

Regional weighted average temperature model considering climate types

LIU Jintao, LYU Weicai, XIAO Xingxing, LU Fukang

（School of Geomatics/Coal Industry Engineering Research Center of Mining Area Environmental and Disaster Cooperative Monitoring/Key Laboratory of Aviation-Aerospace-Ground Cooperative Monitoring and Early Warning of Coal Mining-Induced Disasters of Anhui Higher Education Institutes, Anhui University of Science and Technology, Huainan, AnHui 232001, China）

Aiming at the problem that the atmospheric weighted mean temperature (m) is susceptible to the influence of climate type, latitude and altitude due to the vast land area and complex climate types in China, the paper proposed a regional weighted average temperature model considering climate types: according to the five climate types widely distributed in China, based on the sounding data of 73 sounding stations in China from the year of 2007 to 2015, an atmospheric weighted average temperature model ET-TM model considering climate types, surface air temperature (s) and saturation water vapor pressure (s) was established in different regions; and the accuracy of the ET-TM model was verified by the sounding data of 2016 combined with Bevis model and GPT-3 model. Results showed that the overall accuracy of ET-TM model would be higher than that of Bevis model and GPT-3 model; and the establishment of atmospheric weighted average temperature model by region would be helpful to reduce the influence of latitude and elevation on atmospheric weighted average temperature; furthermore, compared with Bevis model and GPT-3 model, the ET-TM model could be more suitable for the retrieval of atmospheric precipitable water in China.

precipitable water vapor (PWV); atmospheric weighted mean temperature (m); climate type; water vapor retrieval; residual fitting

刘金涛，吕伟才，肖星星，等. 顾及气候类型的区域加权平均温度模型[J]. 导航定位学报, 2023, 11(6): 119-128.（LIU Jintao, LYU Weicai, XIAO Xingxing, et al. Regional weighted average temperature model considering climate types[J]. Journal of Navigation and Positioning, 2023, 11(6): 119-128.）DOI:10.16547/j.cnki.10-1096.20230615.

P228

A

2095-4999(2023)06-0119-10

2023-03-02

2021年度安徽省重大科技专项（202103a05020026）；2021年度安徽省重点研究与开发计划项目（202104a 07020014）；安徽省自然科学基金项目（2008085MD114）。

刘金涛（1998—），男，山东青岛人，硕士研究生，研究方向为GNSS数据处理。

吕伟才（1965—），女，山东青岛人，博士，教授，研究方向为现代测量数据处理、GNSS测量与数据处理。