潮汐对BDS精密单点定位的影响

孟子恒，高 猛，谭春波，曹志华

潮汐对BDS精密单点定位的影响

孟子恒，高 猛，谭春波，曹志华

（辽宁工程技术大学 测绘与地理科学学院，辽宁 阜新 123000）

为了进一步提升精密单点定位（PPP）的精度，研究分析潮汐对北斗卫星导航系统（BDS）精密单点定位的影响：给出固体潮、海潮和极潮改正模型；然后选取全球范围内24个测站，对比分析固体潮、海潮和极潮对BDS精密单点定位的影响。结果表明：1）固体潮对BDS精密单点定位结果影响最大，特别是加入固体潮改正后对高程方向有明显提升。BDS-2在高程方向有45%的测站达到厘米级改正，BDS-3和BDS-2/BDS-3分别有68%的测站和82%的测站达到厘米级改正。2）海潮对沿海测站BDS精密单点定位影响显著，加入海潮改正后沿海测站BDS-2、BDS-3和BDS-2/BDS-3改正量达到毫米级比例数量分别为77%、54%和23%，内陆测站改正量达到毫米级比例的数量分别为27%、9%和9%。3）极潮对BDS精密单点定位影响较小，大部分测站加入极潮改正后在高程方向的改正量为毫米级。

精密单点定位（PPP）；北斗卫星导航系统（BDS）；固体潮；海潮；极潮

0 引言

精密单点定位（precise point positioning，PPP）是一种无需基准站、作业模式灵活、成本低、精度高的定位技术，可为用户提供厘米级甚至毫米级的定位服务[1-4]。2020年北斗卫星导航系统（BeiDou navigation satellite system，BDS）全球组网工作完成，在轨工作卫星包括8颗地球静止轨道（geostationary Earth orbit，GEO）卫星、 10颗倾斜轨道（inclined geosynchronous orbit，IGSO）卫星和27颗中圆地球轨道（medium Earth orbit，MEO）卫星，可为全球用户提供高精度定位、导航和授时服务[5]。目前BDS PPP平面方向的收敛时间和收敛精度约为20 min和1 cm，高程方向的收敛时间和收敛精度约为22 min和3 cm[6]。在PPP中，地球潮汐引起测站坐标随时间的变化是重要的误差源之一[7-8]。随着对BDS应用的精度要求越来越高，研究潮汐对BDS的影响是十分必要的。

目前国内外学者对潮汐进行了相应的研究。文献[9-11]研究了在全球卫星导航系统（global navigation satellite system，GNSS）高精度数据处理中必须消除海潮负荷位移的影响。文献[12]分析了极移对测站的垂向位移有1～2 cm的影响。文献[13]研究了海潮负荷效应在垂直方向上引起的测站位移可达数厘米，此误差在高精度GNSS数据处理中不可忽略。文献[14]基于相关软件分析了固体潮在高程方向对地面测站引起的形变可以达到40 cm。文献[15]研究了在使用GNSS数据进行天顶对流层延迟估计等地球物理反演研究时，必须考虑固体潮的影响。文献[16]分析了海潮负荷的精度主要取决于海潮模型的精度。文献[17-18]分析了不同模型的海潮负荷改正对精密定位影响。文献[19-20]分析了不同海潮模型引起的测站海潮负荷位移差异。文献[21]分析了在中纬度地区，地球固体潮中的长周期项对径向测距的影响可达12.5 cm，造成北方向5 cm的定位系统误差。文献[8]研究了固体潮对BDS PPP的影响，结果表明固体潮是必须考虑的误差改正。

以上研究主要是针对潮汐对全球定位系统（global positioning system，GPS）的影响，目前对BDS影响的研究较少。本文在全球范围内选取内陆和沿海共计24个国际GNSS服务组织（International GNSS Service，IGS）测站，对其2022年第53—59天的数据进行了处理，分别研究了固体潮、海潮和极潮对北斗卫星导航（区域）系统即北斗二号（BeiDou navigation satellite (regional) system，BDS-2）、北斗三号全球卫星导航系统（BeiDou-3 global navigation satellite system，BDS-3）和BDS-2/BDS-3精密单点定位的影响。

1 潮汐改正模型

1.1 固体潮改正模型

太阳和月球对地球的引力产生潮汐现象，潮汐导致整个固体地球产生周期性的形变现象称为固体潮[22]。在相对定位中，利用差分观测值即可消除或削弱其影响。但对于PPP，必须利用模型对固体潮进行改正。固体潮主要考虑二阶潮和三阶潮的影响，其数学改正模型为[23-25]：

1.2 海潮改正模型

海潮是由于太阳和月亮对地球的引力作用使实际的海平面相对于平均海平面产生周期性涨落旳现象。海潮引起海水质量重新分布，从而导致地壳承受荷载，这种负载弹性形变称为海潮负荷。在精密单点定位中，可以采用模型消除海潮的影响。海潮负荷改正模型是通过全球海潮模型提供的海水瞬时潮高与Green函数（地球对单位质量点的负荷函数）的褶积积分求得，因此测站位移的海潮负荷效应公式为[26-27]

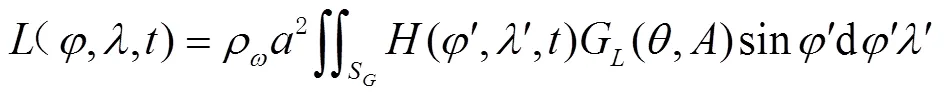
1.3 极潮改正模型

极潮是由地壳对地球自转轴指向极移的弹性响应所引起的地球形变现象。极潮对测站位移影响取决于观测瞬间自转轴与地壳的交点位置，因为极移使地球自转轴指向不断变化，所以交点位置也随时间而变化。因此，在PPP中需要考虑地球极潮的影响。极潮改正的数学模型为[25]

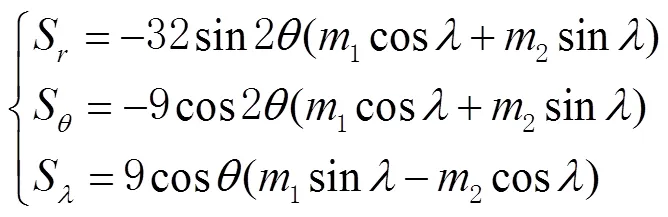
其中

2 实验与结果分析

2.1 数据介绍及处理策略

为分析潮汐对BDS PPP的影响，同时防止测站均处于内陆或沿海导致结果不具有普遍性，分别选取内陆、沿海共计24个IGS测站，测站的位置信息如表1所示。

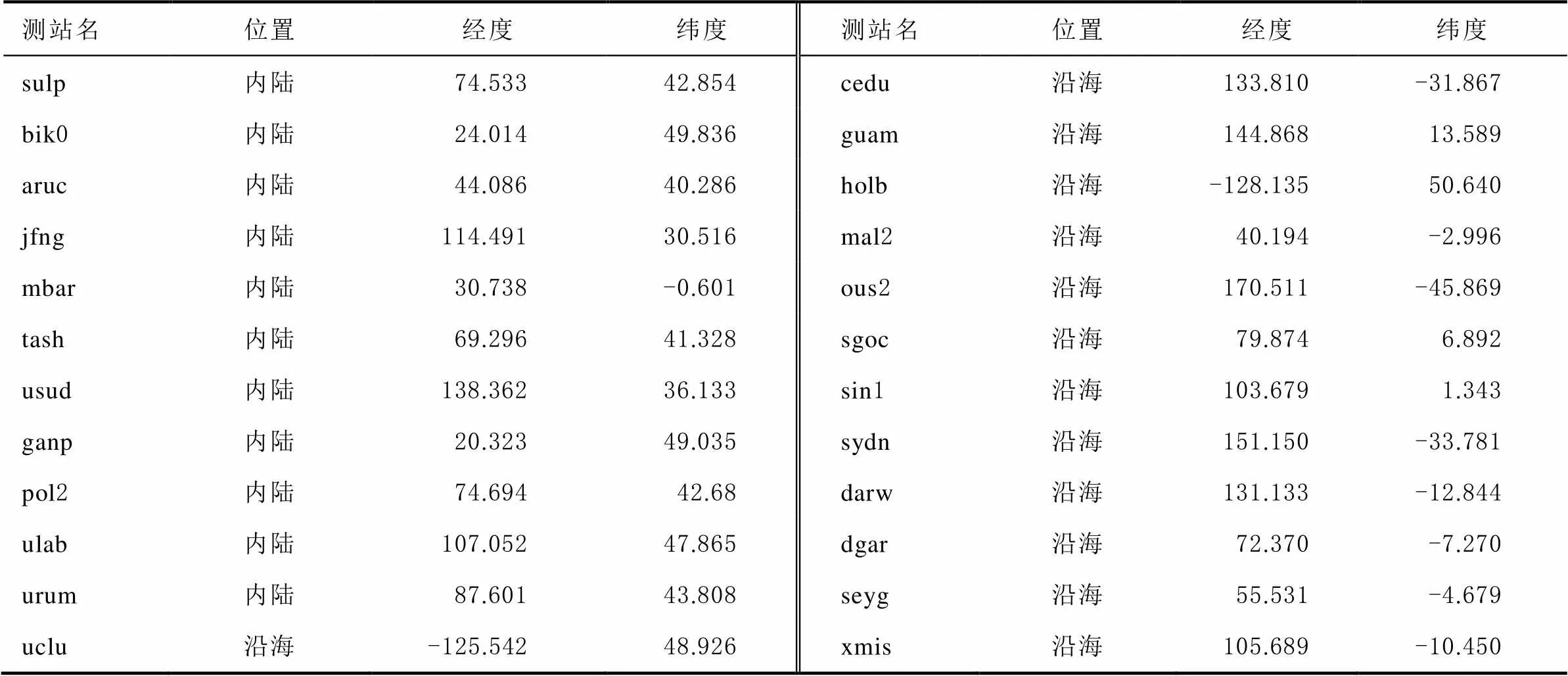
表1 IGS测站具体信息 （°）

对所选取的24个IGS测站进行了BDS-2、BDS-3和BDS-2/BDS-3 PPP处理，实验数据的观测时段选择2022年第53—59天，截止高度角为7°，精密轨道和精密钟差产品选择武汉大学（Wuhan University，WHU）分析中心提供的事后产品，固体潮和极潮采用国际地球自转服务组织（International Earth Rotation Service，IERS）IERS2010协议进行改正，海潮采用法国潮汐小组（French Tidal Group，FTG）提出的有限元解（finite element solution，FES）的FES2004模型进行改正。为了使实验结果更加可靠，对BDS-2、BDS-3以及BDS-2/BDS-3的数据均采用相同的处理策略，具体的PPP处理策略如表2所示。

共设计3组实验方案，分别对BDS-2、BDS-3以及BDS-2/BDS-3加入固体潮、海潮以及极潮改正，并将加入固体潮、海潮以及极潮后得到的定位结果与未进行固体潮、海潮和极潮改正得到的结果进行对比。具体方案如表3所示。

表2 PPP数据处理策略

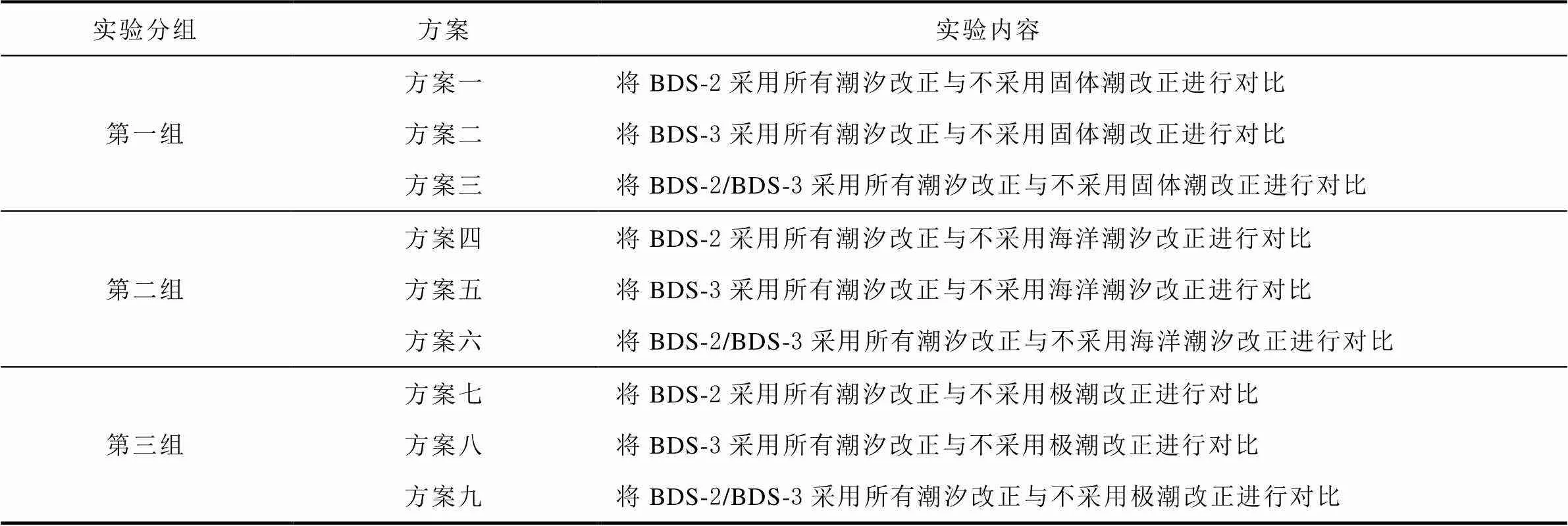
表3 实验设计方案

2.2 固体潮对PPP的影响

针对固体潮对BDS PPP影响的研究，采用方案一、方案二和方案三分别对BDS-2、BDS-3、BDS-2/BDS-3进行固体潮改正，在E（东）、N（北）、U（天顶）方向上的定位结果如图1所示。

由图1可以看出，对于BDS-2，3个方向在加入固体潮误差改正后，定位精度均有明显的提升。24个测站中PPP定位误差最大的是U方向，除了sydn测站的误差在50 cm以上，其他大部分测站的误差在10 cm；其次是E方向；N方向的定位误差最小，其中加入改正后sydn测站的误差增加，是因为在当地连续多天暴雨，导致经验对流层改正模型存在较大误差。对于BDS-3，在未加入固体潮之前U方向的定位误差最大，有41%的测站在未改正之前的误差达到了5 cm以上；其次是E方向，未改正之前的定位误差最大达到6.8 cm；最后是N方向，最大误差达到3.6 cm。对于BDS-2/BDS-3，在未加入固体潮之前U方向的定位误差最大，有14个测站的定位误差在4 cm以上；N方向有9个测站的定位误差在2 cm；对于E方向，sulp测站在未加入固体潮前的定位误差达到了5.5647 cm，xmis测站在未加入固体潮前定位误差为1.1045 cm，其余所有测站的定位结果均在1 cm以下。

将实验所得到的数据做统计分析，如表4所示为对BDS-2、BDS-3和BDS-2/BDS-3加入固体潮改正后，测站在平面和高程方向上的改正量。

从表4可以看出，对于BDS-2，所有测站在加入固体潮改正后定位精度均有提高，其中任一方向达到厘米级改正量的测站达到了86%。U方向在加入固体潮前后的改正量最小值为0.2817 cm，最大值为11.2011 cm；E方向在加入固体潮前后的改正量最小值为0.1156 cm，最大值为9.2287 cm；N方向在加入固体潮前后的改正量最小值为 0.0657 cm，最大值为4.7952 cm。对于BDS-3，有86%的测站在2个及以上方向再加入固体潮改正后定位精度有提高，并且有67%的测站在U方向有厘米级改进，有54%的测站在N方向有厘米级改正，E方向的改正量均在厘米级以下。对于BDS-2/BDS-3，在U方向除usud以及bik0测站，其余测站固体潮均对结果有提升，并且92%的测站有厘米级改正；在N方向有63%的测站有厘米级改正；E方向sulp测站的改正量在5.3111 cm，其余测站的改正量均在毫米级以下。

选取guam（内陆）和sulp（沿海）2个测站，对2个测站2022年第53—59天的数据进行BDS PPP，固体潮对2个测站影响的时间序列如图2所示。

从图2可以看出，固体潮对U方向影响最大。加入固体潮改正后，在U方向改正较明显，这与表4所得结论一致。对于guam测站，除第57天以外，其余6 d在U方向均有明显改正，E方向改正要略优于N方向，但改正量非常小。对于sulp测站，在2022年第53—55天期间，固体潮对U方向的改正不如N方向。总体来看，加入固体潮改正后对测站定位精度有显著提高。

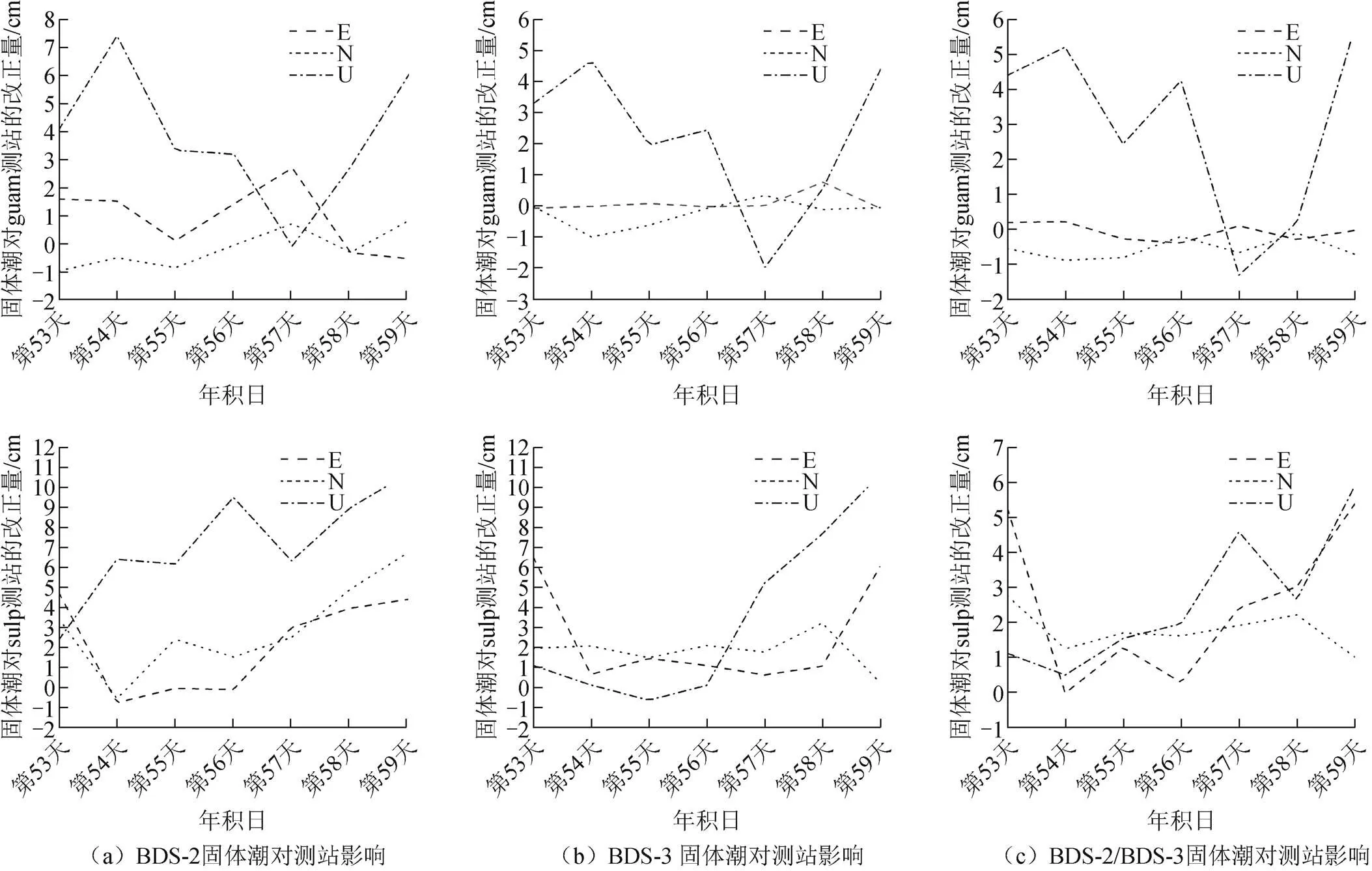
图2 BDS PPP中固体潮对测站影响的时间序列

2.3 海潮对PPP的影响

针对海潮对BDS PPP影响的研究，采用方案四、方案五和方案六分别对BDS-2、BDS-3、BDS-2/BDS-3进行海潮改正，在E、N、U方向上的定位结果如图3所示。

由图3可看出，对于BDS-2，在U方向，sydn测站的定位误差最大，可达46 cm。该测站位于澳大利亚的悉尼，通过查询悉尼天气预报可知，在数据采集时段该地已连续多天暴雨，接收到的BDS-2卫星信号较差，导致高程方向误差很大。其余测站的定位误差均在0.008～0.951 cm。对于BDS-3，U方向的定位误差在0.081～5.087 cm。E方向与N方向相比，N方向定位误差在0.002～0.837 cm，其中误差在0.4 cm以上的测站有8个，E方向定位误差在0.028～1.046 cm，但是E方向误差大于0.4 cm的测站只有6个。对于BDS-2/BDS-3，定位误差最大的是U方向，在0.002～4.423 cm。E方向与N方向相比，N方向定位误差在0.008～0.839 cm，其中误差在0.4 cm以上的测站有6个。E方向定位误差在0.001～0.968 cm，但是E方向误差大于0.4 cm的测站只有5个。

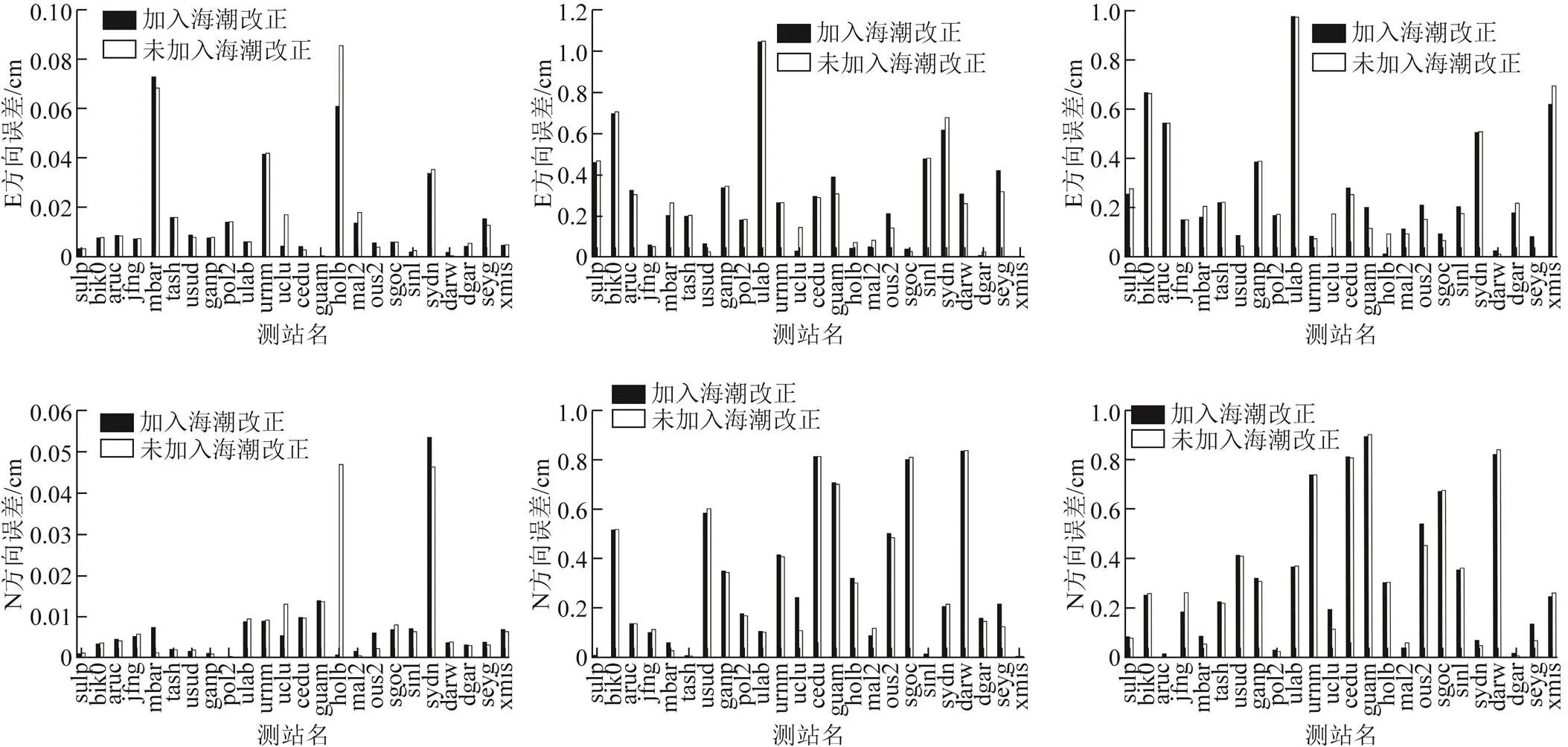
将实验所得到的数据做统计分析，如表5所示为对BDS-2、BDS-3和BDS-2/BDS-3加入海潮改正后，测站在平面和高程方向上的改正量。

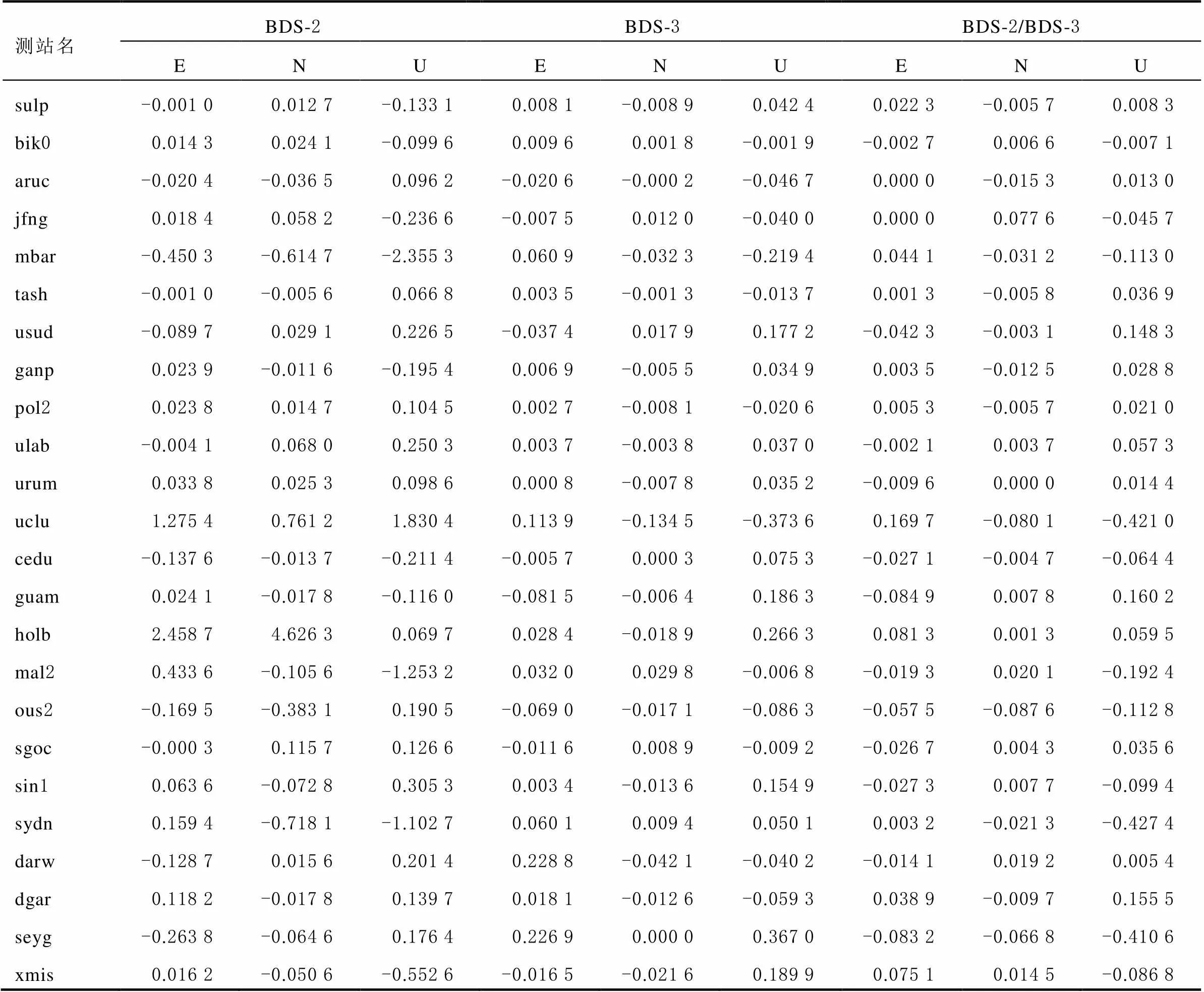
表5 BDS静态PPP海潮对24个测站定位的改正量 cm

由表5可得，对于BDS-2，加入海潮改正后改正量达到厘米级的测站为holb和uclu测站，大部分测站在加入海潮改正后提高精度均在厘米级以下。加入改正后，在E、N、U中1个和2个方向上沿海和内陆测站改正量达到毫米级的比例分别为77%和27%。但是有3个测站在加入改正后反而出现误差有厘米级的提高，出现这种情况的原因有可能是每日海水高潮和低潮的不同导致每日的海潮负荷改正值不同。测站在每个方向上的改正与它相邻海水的高低潮有关系，在高潮时改正效果要优于低潮；也与周边地形有关系，本文所采用的海潮模型在某些测站的相邻海域区域不够精确，所以导致使用该海潮模型解算的海潮负荷并不能改善该测站精度。对于BDS-3，U方向在加入海潮改正后的改正量在0.0349～0.2663 cm，加入海潮改正后在E、N、U中1个和2个方向上改正量达到毫米级的比例分别为54%和9%。对于BDS-2/BDS-3，U方向在加入海洋潮汐改正后的改正量在0.013～0.16 cm，加入海潮改正后在E、N、U中1个或2个方向上改正量达到毫米级的比例分别为23%和9%。

选取guam（内陆）和sulp（沿海）2个测站，对2个测站2022年第53—59天的数据进行BDS精密单点定位，海潮对2个测站影响的时间序列如图4所示。由图可知，海潮对沿海测站的影响要大于内陆测站。在BDS-2精密单点定位中，加入海潮改正后在U方向改正量达到毫米级的天数均为4 d，但是沿海测站的改正量要明显高于内陆测站，并且E方向以及U方向加入海潮改正后有改正的天数也多余内陆测站。在BDS-3精密单点定位中，在加入海潮改正后，guam测站的U方向最大改正量达到0.8 cm，而sulp测站仅有0.1 cm；同样guam测站E方向以及N方向有改正的天数要多于sulp测站。在BDS-2/BDS-3精密单点定位中，加入海潮改正后guam测站U方向最大改正量达到0.5 cm，而sulp站只有0.1 cm；对于E方向和N方向，guam测站有改正的天数也要多于sulp测站。整体上海潮对于沿海测站影响较大，沿海测站应当加入海潮改正，内陆测站可以不用加入海潮改正。

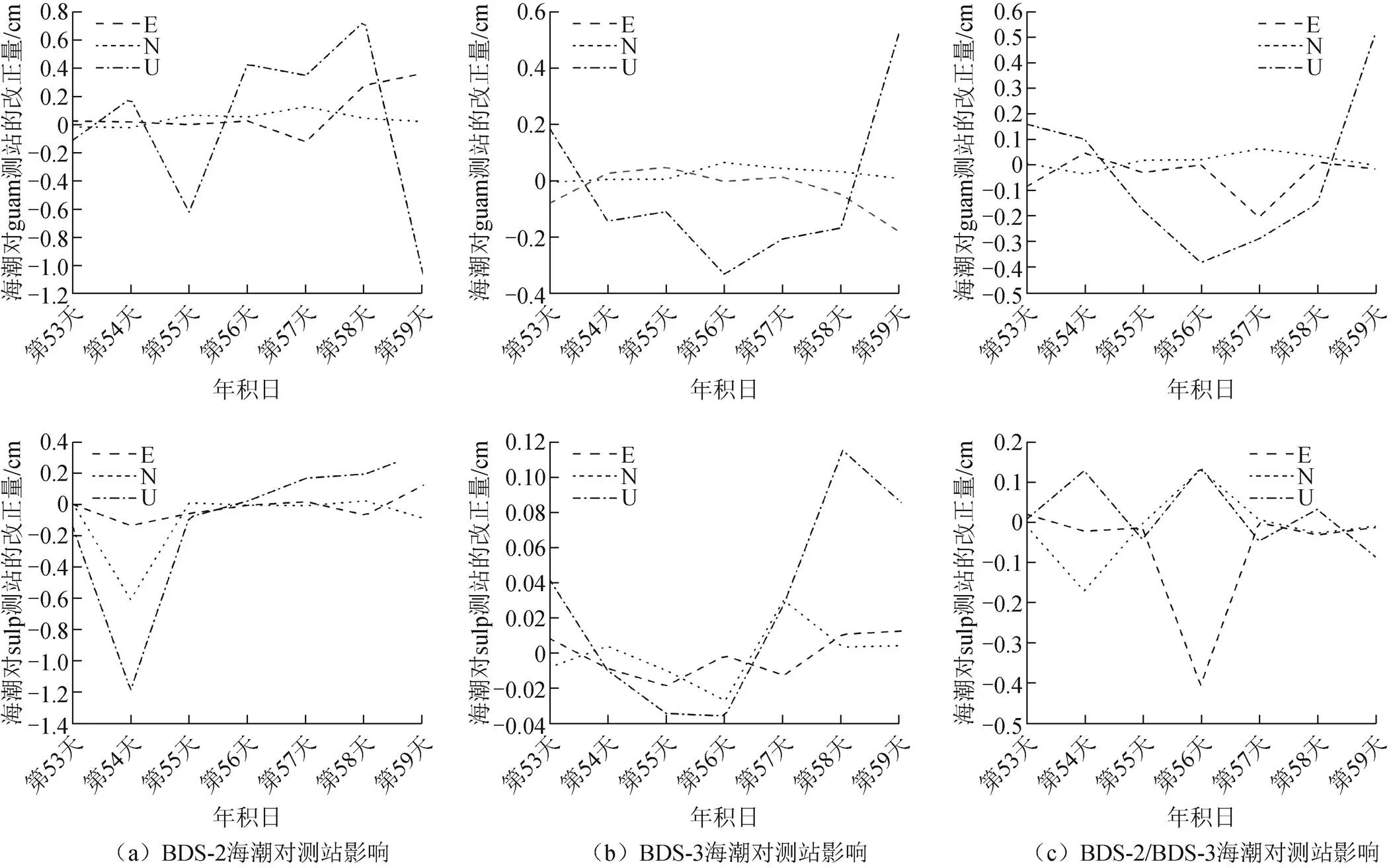
图4 BDS PPP中海潮对测站影响的时间序列

2.4 极潮对PPP的影响

针对极潮对BDS PPP影响的研究，采用方案七、方案八和方案九分别对BDS-2、BDS-3、BDS-2/BDS-3进行极潮改正，在E、N、U方向上的定位结果如图5所示。

由图5可看出，对于BDS-2，在U方向的sydn测站定位误差最大达到47 cm，并且误差整体超过10 cm的测站还有mbar和urum；E方向整体定位结果要优于U方向；N方向定位结果最好，除sydn测站外，其余测站误差均在2cm内。对于BDS-3，U方向的定位误差最大在0.078～4.979 cm；N方向的定位误差在0.011～0.903 cm；E方向的定位误差在0.010～1.143 cm。对于BDS-2/BDS-3，U方向的定位误差最大，在0.035～4.389 cm；N方向的定位误差在0.009～0.879 cm，并且有46%的测站定位误差在0.3 cm以上；E方向的定位误差在0.041～0.932 cm，然而只有21%的测站定位误差在0.3 cm以上，总体来说定位精度要优于N方向。

图5 BDS静态PPP中极潮对E、N、U 3个方向的误差对比

将实验得到的数据做统计分析，如表6所示为对BDS-2、BDS-3和BDS-2/BDS-3加入极潮改正后，测站在平面和高程方向上的改正量。对于BDS-2，加入极潮改正前后对E、N、U方向定位误差改进比较微小，均在亚毫米级以下。对于BDS-3，所有测站都在1个及以上方向在加入极潮后有改正，并且有33%的测站有毫米级改正，改正量最大的是seyg测站的U方向，达到0.7027 cm。对于BDS-2/BDS-3，有79%的测站在加入极潮改正后在1个及以上方向有改正，并且改正量最大的是sydn的U方向，改正量达到0.2529 cm；N方向以及E方向改正量均在亚毫米级及以下。

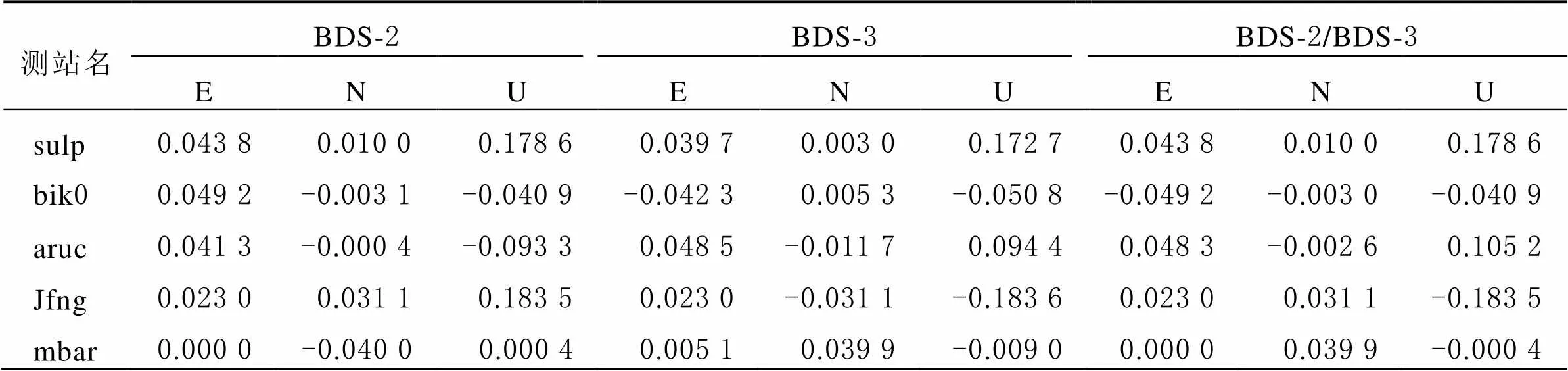
表6 BDS静态PPP极潮对24个测站定位的改正量 cm

（续）

选取guam（内陆）和sulp（沿海）2个测站，对2个测站2022年第53—59天的数据进行BDS PPP，极潮对2个测站影响的时间序列如图6所示。

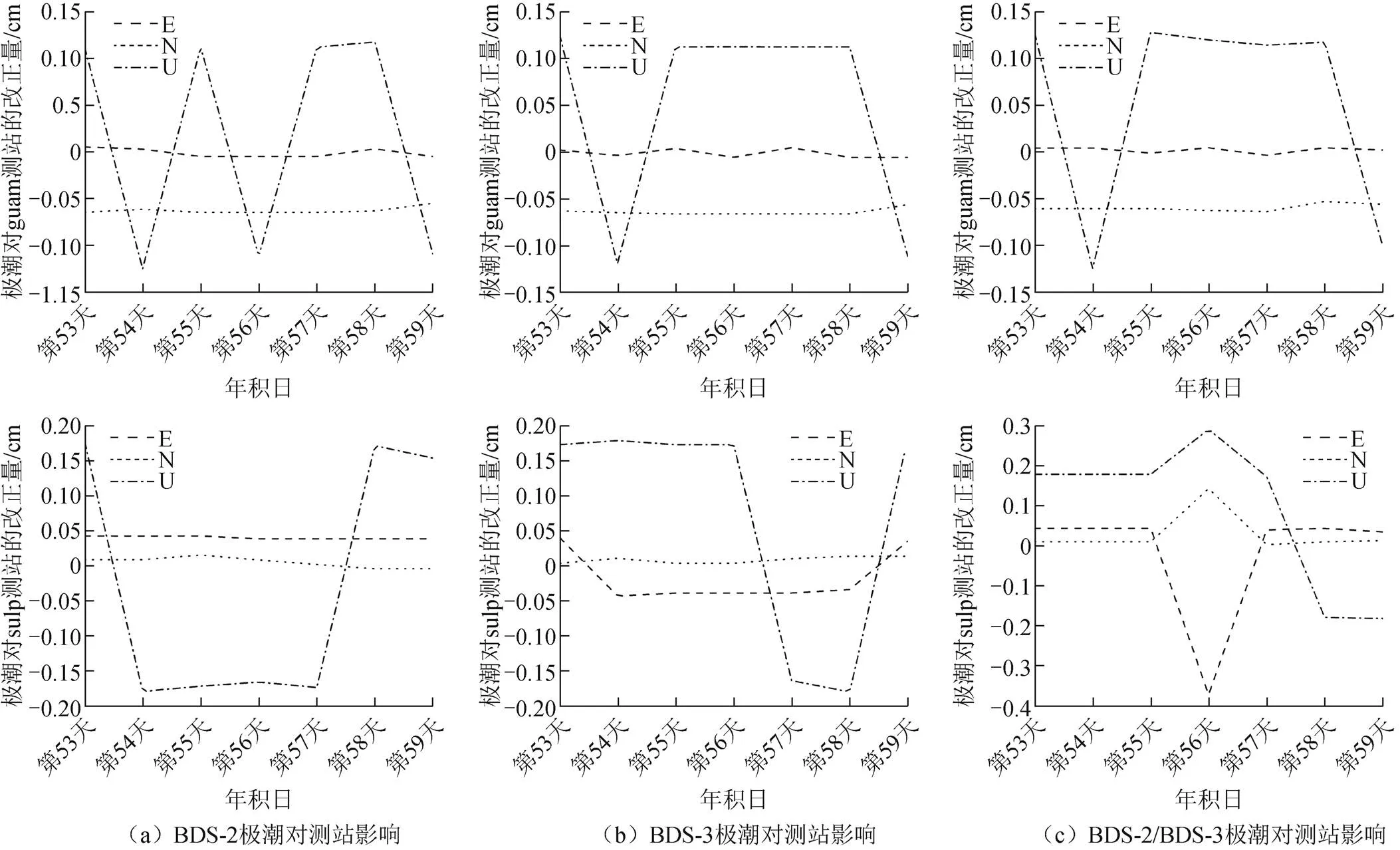
图6 BDS PPP中极潮对测站影响的时间序列

由图6可知，除BDS-2/BDS-3中sulp测站的E方向在2022年第56天改正较差，其余所有时间极潮对2个测站的E方向以及N方向影响非常小，加入改正后定位精度在毫米级以下；对U方向的改正要好于E方向和N方向，改正量可以达到毫米级。整体上极潮对测站的影响最小，E方向和N方向几乎没有影响，在U方向上有2～3 mm波动，对于高精度的BDS PPP应当考虑极潮改正。

2.5 潮汐对GPS PPP的影响

为了验证结论的可靠性，限于篇幅，本文仅选取4个测站进行GPS实验。其中usud和sulp为内陆测站，holb和guam为沿海测站。固体潮、海潮以及极潮对GPS的影响如表7所示。

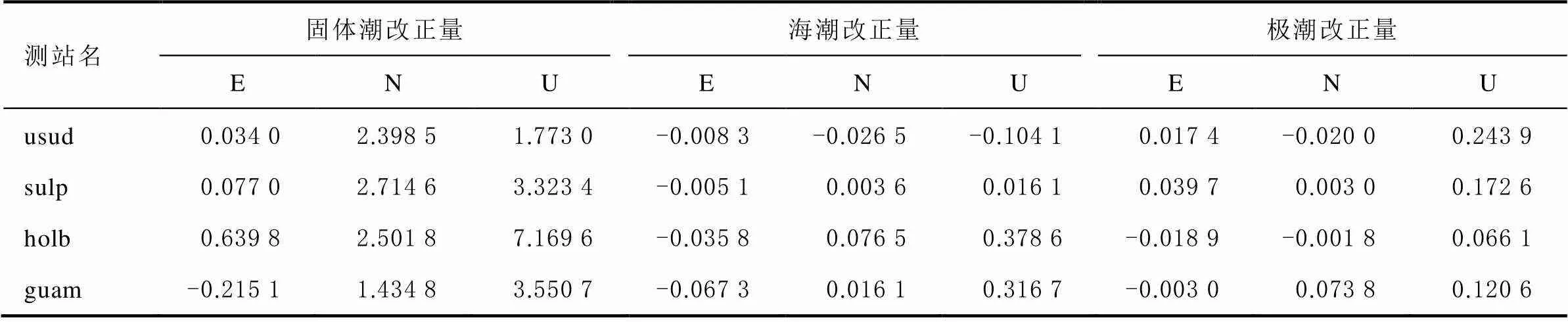
表7 GPS静态PPP潮汐对4个测站定位的改正量 cm

由表7可得，对于GPS系统，在加入固体潮改正后，U方向改正最明显，N方向其次，E方向最少；在加入海潮改正后，对于沿海测站的改正要明显优于内陆测站；极潮对GPS的影响是最小的，在U方向上改正最好的usud测站仅达到0.2439 cm。潮汐改正实际上是潮汐引起测站位置变化进而带来测站位置不一致的问题，因此理论上GPS与BDS的潮汐改正应相同，通过GPS实验与BDS实验验证了2个导航系统改正会略有差异，但大致相同。

3 结束语

本文分析了固体潮、海潮、极潮对BDS-2、BDS-3、BDS-2/BDS-3 PPP的精度影响并得出结论：

1）固体潮对BDS PPP结果有显著影响，在加入固体潮改正后均有明显改善，并且在U方向的改善效果最为明显。BDS-2在U方向有71%的测站有厘米级以上改正；BDS-3在U方向有67%的测站达到厘米级以上改善；BDS-2/BDS-3有79%的测站在U方向达到厘米级改正，在N方向有63%的测站达到厘米级改正，在E方向大部分测站的改正效果在毫米级。

2）海潮对BDS PPP精度的影响较小，但是对于沿海测站影响要明显大于内陆测站，沿海测站必须加入海潮改正。在加入海潮改正后BDS-2沿海和内陆测站达到毫米级改正的测站比例分别为77%和27%；BDS-3加入海潮改正后达到毫米级改正的测站的比例分别为54%和9%；BDS-2/BDS-3加入海潮改正后改正量达到毫米级改正的测站比例分别为23%和9%。

3）极潮对BDS PPP的影响非常小。在BDS-2中，加入极潮后达到毫米级改正的测站仅占37%，其余测站的改正量均在亚毫米级及以下；在BDS-3中有33%的测站在加入改正后改正量达到毫米级；在BDS-2/BDS-3中仅有30%的测站改正量达到毫米级。

本文进行的是潮汐对BDS系统的影响分析，在今后的研究中还将针对潮汐对GPS/格洛纳斯全球卫星导航系统（global navigation satellite system，GLONASS）/伽利略卫星导航系统（Galileo satellite navigation system，Galileo）/BDS等4个系统的影响进行细致的分析。

[1] 屈利忠, 赵齐乐, 郭靖, 等. GNSS融合动态精密单点定位性能分析[J]. 大地测量与地球动力学, 2016, 36(4): 298-302.

[2] 张小红, 李星星, 李盼. GNSS精密单点定位技术及应用进展[J]. 测绘学报, 2017, 46(10): 1399-1407.

[3] ZUMBERGE J F, HEELIN M B, JEFFERSON D C, et al. Precise point positioning for the efficient and robust analysis of GPS data from large networks[J]. Journal of Geophysical Research, 1997, 102(B3): 5005-5017.

[4] KOUBA J, HéROUS P. Precise point positioning using IGS orbit and clock products[J]. GPS Solutions, 2001, 5(2): 12-28.

[5] 李星星, 张伟, 袁勇强, 等. GNSS卫星精密定轨综述:现状、挑战与机遇[J]. 测绘学报, 2022, 51(7): 1271-1293.

[6] 朱少林, 岳东杰, 何丽娜, 等. BDS-2/BDS-3融合三频精密单点定位模型及偏差特性分析[J/OL]. 武汉大学学报(信息科学版): 1-15[2022-11-20].

[7] 赵红, 张勤, 徐超, 等. 潮汐效应对香港地区GPS PPP的影响[J]. 大地测量与地球动力学, 2016, 36(1): 6-10.

[8] 李艳红, 成芳, 沈朋礼, 等. 固体潮对BDS精密单点定位的影响研究[J]. 测绘科学, 2022, 47(1): 66-75.

[9] DZIEWONSKI A M, ANDERSON D L. Preliminary reference Earth model [J]. Physics of the Earth and Planetary Interiors, 1981, 25 (4): 297-356.

[10] DEHANT V, DEFRAIGNE P, WAHR J. Tidess for a connective Earth [J]. Journal of Geophysical Research: Solid Earth, 1999, 104 (B1): 1035-1058.

[11] BLEWITT G, LAVALL E D, CLARKE P, et al. A newglobal mode of Earth deformation: Seasonal cycle detected [J]. Science, 2001, 294 (5550): 2342-2345.

[12] 王解先. GPS精密定轨定位[M]. 上海: 同济大学出版社, 1997.

[13] VEY S, CALAIS E, LLUBES M, et al. GPS measurements of ocean loading and its impact on zenith tropospheric delay estimates:A case study in Brittany,France[J]. Journal of Geodesy, 2002, 76(8): 419-427.

[14] MCCARTHY D D, PETIT G. IERS conventions(2003): No.IERS-TN-32[S]. Frankfurt am Main, Germany, 2004.

[15] 刘根友. 高精度GPS测量中的潮汐改正[C]// 2004年重力学与固体潮学术研讨会暨祝贺许厚泽院士70寿辰研讨会. 武汉: 湖北科学技术出版社, 2004: 398-406.

[16] 袁林果, 丁晓利, 孙和平, 等. 利用GPS技术精密测定香港海潮负荷位移[J]. 中国科学:地球科学, 2010, 40(6): 699-714.

[17] 赵红, 张勤, 黄观文, 等. 基于不同海潮模型研究海潮负荷对GPS精密定位的影响[J]. 大地测量与地球动力学, 2012, 32(5): 108-112.

[18] 何金鑫, 章浙涛, 何秀凤. FES2004和GOT4.7海潮模型改正对全球PPP的影响特征及差异分析[J]. 大地测量与地球动力学, 2021, 41(6): 612-617.

[19] 赵大江, 郭春喜, 程传录, 等. 不同海潮模型对GNSS站负荷位移计算的影响[J]. 大地测量与地球动力学, 2016, 36(7): 654-658.

[20] 范文蓝, 姜卫平, 袁林果, 等. 不同海潮模型对中国沿海区域海潮负荷位移改正影响分析[J]. 大地测量与地球动力学, 2018, 38(6): 598-602.

[21] 戴志强. GNSS实时精密定位服务系统若干关键技术研究[D]. 武汉大学, 2016.

[22] AGNEW D. Earth tidess[J]. Treatise On Geophysics, 2007, 3(6): 163-195.

[23] 殷海涛, 李杰, 马丕峰, 等. 固体潮模型对GPS时间序列的影响研究[J]. 大地测量与地球动力学, 2009, 29(2): 48-52.

[24] MCCARTHY D D, PETIT G. IERS conventions(2003)[R]// IERS Technical Note32,Verlag des Budesamts fur Kartographie and Geodasie. Frankfurt, 2004.

[25] 赵红. 海潮负荷效应及利用GPS技术建立海潮负荷位移模型研究[D]. 长安大学, 2016.

[26] FARRELL W E. Deformation of Earth by surface loads[J]. Rev Geophys SpacePhys, 1972, 10(3): 761-797.

[27] 张化疑. 基于GNSS的海潮负荷位移研究[D]. 武汉大学, 2020.

Effect of tidal correction on BDS precise point positioning

MENG Ziheng, GAO Meng, TAN Chunbo, CAO Zhihua

（School of Geomatics, Liaoning Technical University, Fuxin, Liaoning 123000, China）

In order to further improve the accuracy of precise point positioning (PPP), the paper studied the effect of tidal correction on BeiDou navigation satellite system (BDS) PPP: the correction models of Earth solid tide, ocean tide and polar tide were given, and 24 stations around the world were selected to comparatively analyze the impact of solid tide, ocean tide and polar tide on BDS PPP. Results showed that: 1) the solid tide would have the greatest influence on the BDS PPP, especially the elevation direction could be obviously corrected after adding the solid tide correction, among which for BDS-2, 45% of the stations in the elevation direction would achieve centimeter level correction, and for BDS-3 and BDS-2/BDS-3, 68% and 82% of the stations would reach centimeter level correction, respectively; 2) the ocean tide would have a significant impact on BDS PPP of the coastal survey stations, that is, after adding the ocean tide correction, the percentage of corrections of the coastal stations of BDS-2, BDS-3 and BDS-2/BDS-3 reaching the millimeter level would be 77%, 54% and 23%, respectively, and the percentage of corrections of inland stations reaching millimeter level would be 27%, 9% and 9%, respectively; 3) pole tide would have little impact on BDS PPP, and most stations could have millimeter level correction in elevation direction after adding pole tide correction.

precise point positioning (PPP); BeiDou navigation satellite system (BDS); solid tide; ocean tide; pole tide

孟子恒, 高猛, 谭春波, 等. 潮汐对BDS精密单点定位的影响[J]. 导航定位学报, 2023, 11(6): 64-75.（MENG Ziheng, GAO Meng, TAN Chunbo, et al. Effect of tidal correction on BDS precise point positioning[J]. Journal of Navigation and Positioning, 2023, 11(6): 64-75.）DOI:10.16547/j.cnki.10-1096.20230609.

P228

A

2095-4999(2023)06-0064-12

2023-03-13

国家自然科学基金项目（41904037）。

孟子恒（2000—），男，辽宁鞍山人，硕士研究生，研究方向为BDS/GNSS精密单点定位算法。

高猛（1988—），男，辽宁康平人，博士，副教授，研究方向为GNSS高精度定位算法。