虚拟养老服务人员调度多目标优化研究＊

廖 阳，孟豪南，李迎峰

(西安建筑科技大学管理学院，陕西 西安 710055)

0 引言

虚拟养老是在传统居家养老的基础上采用信息化、智能化的设备快速、精准地把握老人的服务需求。近些年，虚拟养老院在我国多个城市落地，其市场需求扩大的同时也对服务质量提出了更高的要求。更好的服务、更低的成本是虚拟养老院能够长期健康发展的关键。这其中，服务人员的调度问题是控制成本，提高服务质量的关键一环。

虚拟养老具有服务的属性，这就要求不能仅以成本大小作为评判调度方案优劣的唯一标准。由于老人和服务人员都是重要的参与主体，对虚拟养老事业发展起到关键作用。因此在制定调度方案时，需要明确这两者的利益追求，在控制成本的同时兼顾这两者的利益。当前针对虚拟养老问题的研究，学术界普遍是定性研究，其研究内容主要包括对发展路径[1]和存在问题[2]的总结。

本文研究的虚拟养老服务人员调度问题从属于养老护工调度问题(home health care routing problem，HHCRP)[3]。当前学术界已取得了一定的研究成果。从研究目标来看，各研究的立足角度有所不同，包括但不限于立足服务机构的成本优化[4-6]和立足客户的满意度优化[7-9]，无论是单目标的成本优化或是多目标优化都有较为丰富的研究成果值得借鉴。从求解算法来看，本问题同属于NP-hard，当前学者较多采用精确式算法[10-11]和元启发式算法[12-17]。但随着约束条件和问题研究的复杂化，精确式算法难以有效求解，相比之下，元启发式算法更加适合本问题的求解，主要包括：蚁群算法[12]、遗传算法[13]、布谷鸟算法[14]、萤火虫算法[15]、模拟退火算法[16]和memetic 算法[17]等。此外，机器学习[18]也可用于问题求解。本文的研究从老人、服务中心和服务人员的角度出发，通过分析三者的利益追求，并以成本最优、老人和服务人员满意度最大为优化目标，建立多目标优化模型。

本文首先针对调度问题制定决策依据；其次把握老人服务需求信息，设计求解算法，提高算法的运行效率。本文的第一部分是对研究问题进行数学建模，第二部分提出了求解本问题的优化算法。第三部分通过求解算例来验证算法的性能，第四部分总结本文的研究工作并提出研究展望。

1 优化模型

1.1 满意度函数

⑴老人的满意度函数

由于老年人的身体和感情等原因，部分老人特别是需要医疗服务的老人会对服务开始的时间更加关注，因此能否在老人理想的时间段内提供服务尤为重要。此外，对服务人员偏好也是影响老人满意度的重要因素，一般来说，有的老人会对某一位或某几位服务人员有特殊的情感，更乐于接受其服务。基于以上讨论，本文构建老人服务满意度函数其中α1 和α2 为权重参数分别为老人的时间满意度函数和对服务人员偏好的满意度函数。

①时间满意度函数：

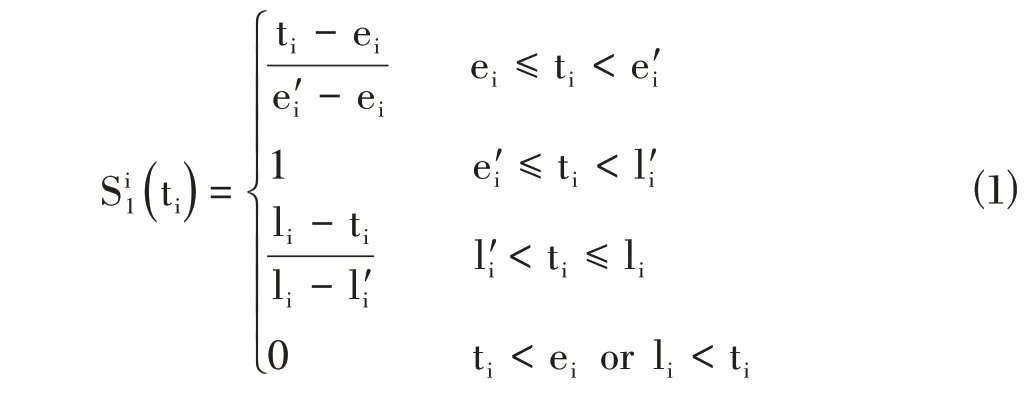
其中，ti为老人i 接受服务的时间，同时采用混合时间窗，其中e'i和l'i为老人i 理想的服务时间段，在此期间老人接受服务满意度为1，ei和li为老人能够容忍的时间段，在此期间老人的服务满意度会有所下降，当开始服务时间超出这段范围后，老人的满意度为0，并将产生高额的惩罚成本。时间满意度函数如图1所示。

图1 时间满意度函数

②对服务人员偏好的满意度函数：

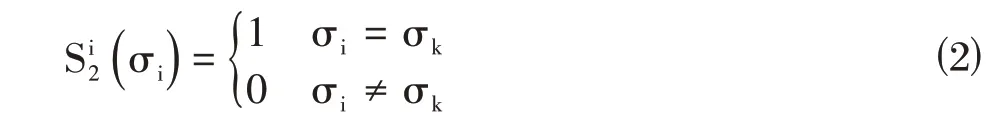
其中，σi为老人i 偏好的服务人员集合，σk为服务中心安排给老人i 的服务人员。当该服务人员属于能够满足老人对服务人员的偏好时，老人的满意度为1，当不满足时，老人的满意度为0。

⑵服务人员的满意度函数

从服务人员的角度来看，任务量分配是影响满意度的重要因素。服务中心需合理的安排各服务人员的任务量，避免各服务人员之间任务量相差过大产生不满情绪，进而会影响服务质量，因此，合理安排任务也是制定调度方案时必须考虑的重要因素。

本文构建如下的服务人员满意度函数如下：

当服务人员k 的任务量未超出a 时，其满意度为1；当任务量超过a 而未超过b 时，此时其满意度时其满意度会降低；当任务量超过b时，此时服务人员的满意度为0，降为最低。服务人员满意度图像见图2。

图2 服务人员满意度函数

1.2 模型构建

式⑷为服务中心的总成本最低，其中的cf为惩罚成本。TD为当前调度方案的总距离，cd为单位距离成本，α为单位等待成本，β为单位迟到成本。式⑸为所有老人的满意度最大；式⑹为所有服务人员满意度最大；式⑺和式⑻为服务人员从服务中心出发完成服务后回到服务中心式⑼为每位老人只接受一个服务服务；式⑽为服务时间窗约束，其取值范围为老人所容忍的时间范围，并将其设置软约束；式⑾为0-1 决策变量表示服务人员k完成老人i服务后服务老人j。

2 多目标鲸鱼优化算法

鲸鱼优化算法是Mirjalili 和Lewis 在2016 年提出的群体智能优化算法[19]，具有操作简单，调整的参数少以及跳出具有最优等优点。其思想是模拟自然界中鲸鱼的捕食行为。在鲸鱼群觅食过程中，通常会有一条或多条鲸鱼率先发现猎物，此时其他鲸鱼就会向该鲸鱼靠近，从而完成捕食行为。传统的鲸鱼优化算法一般用于连续性寻优问题，而求解本文的离散化多目标优化问题需要加以改进，具体的步骤如下。

⑴编码与解码

编码和解码是算法设计的前提工作，本文的研究是优化目标中求解服务人员的调度方案，属于离散化问题求解，因此本文采用自然数编码的形式，以代表老人的编号。以6 名老人和2 名服务人员为例，编码方案如图3所示。

图3 编码方案

图4 中，服务人员1 的服务路线为0→1→4→5→6→0，服务人员2 的路线为：0→2→3→0，不同路径中用101,102，……，用于分隔，其中分隔数的第三位数对应着服务人员的编号，方便用于老人对服务人员偏好满意度的求解。

⑵鲸鱼群位置更新

传统鲸鱼优化算法中，鲸鱼群固定公式进行位置更新，并根据A1的取值范围来决定鲸鱼i 靠近选择。由于本文求解的连续性问题难以直接应用本节研究，因此需要对鲸鱼优化算法的位置更新公式进行改进。在传统鲸鱼优化算法中，优化过程的前中期，鲸鱼种群会更多的选择随机鲸鱼个体靠近，以增加算法的全局搜索能力，而当优化过程进入中后期，鲸鱼种群会更多的向最优鲸鱼个体靠近，避免种群中优良解遭到破坏。综合以上考量，本文采用遗传算法中的交叉算子来替代鲸鱼的位置更新公式，通过设置动态概率为鲸鱼个体选择待交叉个体。

⑶局部搜索算子

本文采用4种局部搜索算子(insert,swap,inverse,2-opt),来提高算法的局部搜索能力，下面介绍这4 种搜索算子。

①insert算子：随机选择两个节点i，j，并将i插入j之后。

②swap 算子：随机选择两个节点i，j，并交换i 和j的位置。

③inverse 算子：随机选择两个节点i，j，并将i 与j之间的节点进行反转。

④2-opt 算子：随机选择两个节点i，j，并将包括两个节点在内的节点进行反转。

⑷非支配排序

不同于单一目标优化问题，多目标优化问题求解过程中其各个目标往往会产生矛盾，导致难以衡量解的优劣，通常情况下可以通过求解该问题的非支配解构成的Pareto最优解集来达到目标。第三代非支配排序遗传算法(NSGA-III)是Deb[20]在NSGA-II 算法的基础上做出改进。两种算法都是针对多目标优化问题，其算法流程大致相同，但两种算法的选择机制有所不同，NSGA-II 利用拥挤距离来选择相同等级个体,而NSGA-III 利用分布良好的参考点来维持种群的多样性。已有的研究佐证，NSGA-III 相较于NSGA-II 在求解多目标优化问题能够取得更好的结果[21]。考虑到本文求解的三目标优化问题，我们采用NSGA-III 算法中的快速非支配排序和选择机制。因受限于篇幅，具体的步骤可见文献[22]，本文在此不再赘述。

3 仿真分析

3.1 算例求解

本文通过求解算例来验证设计算例的有效性。由于没有测试的标准例题库，故本文选择标准例题中C101中35个客户点作为本文的求解算例[23]，并在原算例的基础上对所有老人添加了服务人员的偏好集合以及老人可容忍的时间窗。在某市的二维平面内，有一处虚拟养老服务中心位于(40,50)，该服务中心共有6 名服务人员，共有35 个老人分布在该平面上。本文在Windows10 操作系统，内存为8G，处理器为英特尔Core i7-6700HQ 的计算机上采用Matlab R2016a 来编程。文中设置的参数见表2。

表2 模型和算法参数设置

经过求解，共求得23 个Pareto 最优解，由于篇幅限制，本文从中选择出成本最优的调度路线图解用于展示，其服务路线图如图4所示。

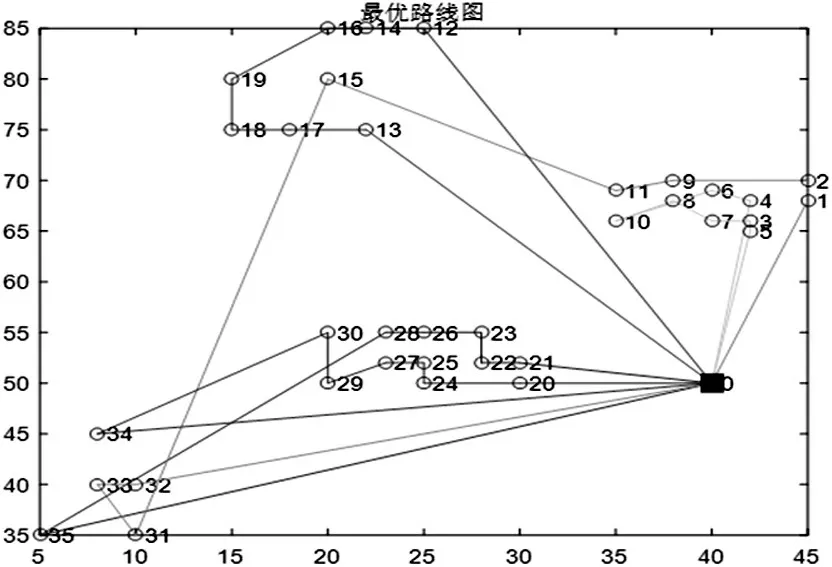
图4 成本最优的服务路线图

3.2 算法性能对比

为了验证本文构建的DMO-WOA 算法的优越性，本文同时采用NSGA-II 和NSGA-III 算法作为参照，并采用Spacing和C两个指标评价算法的性能。其中Spacing指标表示解集分布的均匀性，指标值越小则说明得到的解集分布越均匀,C 指标计算的是一个解集中的解至少被另一个参照解集中的一个解弱支配的比例，用于衡量的是两个解集之间的重合程度，结果如表3所示。

表3 算法性能对照

从表3 能够看出，无论是最优解的数量或是接解得空间的分布，本文设计的DMO-WOA 算法相较于NSGA-II 和NSGA-III 具有良好的性能，为了更直观地对比这三种算法的性能，本文绘制了三种算法求解的箱型图如图5所示。

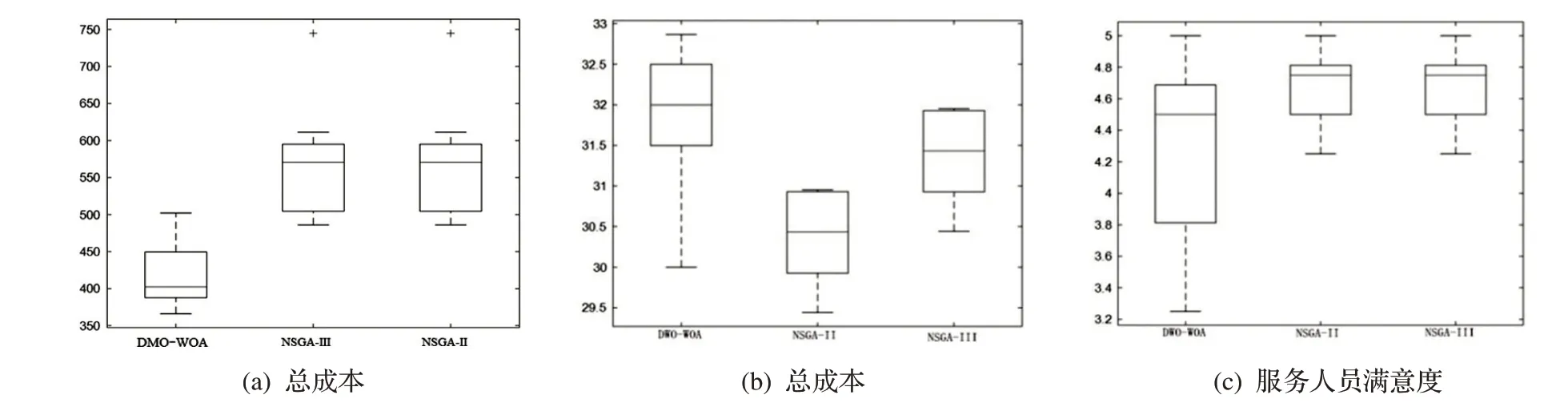
图5 箱型图

从结果来看，相较于对照的NSGA-II 和NSGAIII 算法，本文DMO-WOA 算法在控制服务中心成本、提升老人满意度上有显著效果。由于服务人员满意度目标取值空间较前两者更紧凑些，所以，箱形图并未表现出明显优势。总体来看，本文的DMO-WOA算法对于求解本文问题具有显著优势。

4 结论与展望

本文针对虚拟养老服务人员调度问题，通过分析老人、虚拟养老服务中心和服务人员的利益追求，并以成本最优、老人满意度最大和服务人员满意度最大构建多目标优化模型；设计了离散化多目标鲸鱼优化算法，同时利用NSGA-II 算法和NSGA-III 算法进行对比分析，并通过求解算例验证了本文算法的优越性。本文的研究是针对老人需求确定情况下的服务人员调度问题，未来将从动态视角对服务人员实时调度问题展开研究。