基于IPSO-SVM的大气候室相对湿度预测＊

丁瑞成，刘 斌，郑焕祺，周玉成,

(1.山东建筑大学信息与电气工程学院，山东 济南 250101；2.山东省产品质量检验研究院；3.山东建筑大学建筑城规学院)

0 引言

大室法检测人造板及其制品释放的甲醛，需要模拟出一个具有恒定温湿度的室内环境。由于甲醛检测用大气候室容积较大，影响温湿度的因素较多且具有强耦合、时变和非线性等特性，此类控制系统温湿度控制效果滞后现象明显[1]，相对湿度这一问题尤为突出。若能基于影响因素来预测大气候室相对湿度的变化，对于控制策略设计具有一定的参考意义。

随着机器学习的兴起，一些学者通过智能算法来建立温湿度预测模型，并基于模型设计相应的控制策略。Attoue 等人[2]提出了一种基于人工神经网络的室内温度预测模型，并以此设计控制策略来优化调节建筑能源设备。Moon 等人[3]设计了一种基于人工神经网络的室内温度预测控制算法，通过预测不同空闲时间段的冷却能耗与温度恢复至设定值的响应时间来优化控制策略，仿真结果表明该控制算法能提供更舒适、节能的室内环境。在国内，张永芳等人[4]建立了基于径向基网络的日光温室温湿度预测模型，并采用麻雀搜索算法优化参数，取得了较高的预测精度。倪凡等人[5]分别运用网格搜索法、遗传算法和粒子群算法三种智能优化算法进行SVM 参数寻优，预测储粮横向通风过程中的粮堆温度场，结果表明PSO-SVM 模型的预测误差最小。

虽然标准的PSO 算法具有早期收敛速度快，寻优精度高等优点，但是容易过早收敛，陷入局部最优解[6-8]。针对这些不足，刘文贞等人[9]引入一种基于适应度的粒子变异机制，当粒子过于聚集时，对最优值施加随机扰动。柴文光[10]通过混沌序列初始化粒子的位置与速度，并在原本全局最优值的基础上引入混沌搜索半径。王宏伟等人[11]提出一种动态感知双子群PSO算法，两个子群采取相反的搜索方向，并保留适应度更优的粒子。这些改进策略扩展了种群的搜索空间，提高了算法跳出局部最优的概率。

基于此，本文提出IPSO算法三种改进策略如下：

⑴ 采用Tent 混沌映射初始化种群，增加种群多样性；

⑵采用新的惯性权重更新策略，有效平衡算法的全局搜索与局部搜索能力；

⑶引入SFLA 算法的跳跃机制，增强算法的全局搜索能力，避免种群陷入局部最优值。

基于IPSO 算法优化SVM 参数，应用于大气候室相对湿度预测，并与PSO-SVM、GA-SVM 进行预测效果对比，采用大气候室真实运行时记录的温湿度数据，实验结果验证了IPSO-SVM 模型拥有最优秀的泛化性能与预测精度。

1 IPSO算法

粒子群优化算法原理：在粒子探索过程中，种群中各个粒子不断交流个体认知与群体认知，前者代表了当前粒子的个体最优值，后者代表了当前种群最优值。粒子依据这两个极值在下一次迭代时更新速度与位置，直至满足迭代终止条件。粒子更新速度和位置的公式如下：

1.1 Tent映射初始化种群

标准PSO 算法是采用随机方式初始化种群，存在降低种群多样性，陷入局部最优的风险，而混沌运动具有随机性、规律性和遍历性的特征，利用其初始化种群，有利于维持种群多样性，增强全局搜索能力[12]。具有代表性的混沌映射有Logistic 映射，Tent 映射等，而Tent 映射在规律性、均匀性和迭代速度等方面优势更加突出[13]。因此本文采用Tent 映射，将得到的混沌序列zk代替随机数初始化种群，并映射至搜索空间，其数学公式为：

生成的混沌序列zk∈[0,1]，用于初始化种群位置Xk，如下式所示：

其中，ub与lb为搜索空间的上界与下界。

1.2 非线性惯性权重策略

ω很大程度上影响着种群的全局搜索与局部搜索能力，对于算法性能的提高至关重要[14-16]。本文引入一种新的ω非线性递减策略为：

其中，ωi为初始值；ωe为最终惯性权重；k为当前迭代步数；T为最终迭代步数。

本文对ω的仿真如图1 所示。由图1 可以看出，ω衰减速度随迭代步数逐渐加快，在粒子迭代前期，ω取值较大且衰减速度较慢，粒子全局搜索能力较强，有利于维护种群的多样性。在迭代后期，ω取值较小且衰减速度加快，粒子局部搜索能力较强，有利于加速种群收敛。本文提出的ω自适应非线性递减策略可以很好的平衡种群的全局搜索与局部搜索能力。

图1 非线性ω变化曲线

1.3 引入SFLA跳跃机制

Eusuff 等人与2003 年提出了SFLA 算法，该算法具有鲁棒性强，拥有较好的全局搜索能力和较快的收敛速度等优点[17]。SFLA 蛙群种群数为N，依照适应度优劣排列后平均分为k组子群，每组最差蛙的跳跃机制如下：

其中，i∈[1,2…d]表示搜索空间的维度；Di为跳跃步长；Xib为适应度最优的个体位置；Xiw为适应度最差的个体位置；rand()为0到1之间的随机数。

SFLA 中Xib首先为该组最优个体的位置，最差蛙向其方向跳跃，当适应度未改善时，Xib为整个蛙群适应度最优个体位置，若适应度仍未改善，最差蛙随机跳向搜索空间内一个位置。由于SFLA 跳跃机制中Xib与PSO 算法的Pibest、Pgbest类似，均是由适应度最优个体引导种群的进化方向，种群跳出局部最优的能力较弱。本文在此基础上，参考SFLA 第三次随机跳跃，定义跳跃因子Lm如式⑻所示，将粒子的收敛程度与当前迭代步数作为是否触发跳跃机制的依据，当满足判定条件Lm＜rand(0,1)时，对于粒子的位置更新施加随机扰动，如式⑼若粒子跳跃后位置Xi'适应度值优于跳跃前Xi，则更新粒子位置，否则保持位置不变。

其中，k是当前迭代步数；davg是所有粒子距离全局最优粒子δ的平均距离为粒子搜索范围内的随机位置。α是调节因子，用于平衡k与davg对于Lm的影响能力，经实验表明α取值[0.015,0.035]效果较好，本文取值0.02。

1.4 IPSO-SVM参数寻优

本研究SVM 采用径向基核函数，利用IPSO 算法对SVM 的惩罚系数C和核参数g进行优化，选用最小化均方误差Fmse作为目标函数，有：

其中，n为样本个数；f(xi,c,g)为气候室温湿度预测模型输出；yi为真实温湿度。

选择适应度函数：

IPSO算法寻优SVM具体步骤如下：

步骤1初始化粒子的速度Vi与位置Xi和IPSO 算法参数，包括：种群规模N，最大迭代步长T，惯性权重ω极值，学习因子c1、c2，粒子搜索范围与速度范围。依据式(10)计算粒子的适应度值，更新初始个体最优值Pibest与全局最优值Pgbest。

步骤2使用式⑻计算跳跃因子Lm，生成随机数β∈[0,1]，如果Lm＜β，使用式⑼更新粒子位置计算新的适应度值Ff'itness。

步骤3使用式(1-2)更新粒子的速度V ik+1与位置，计算适应度值Ffitness。

步骤4如果＜Ffitness，粒子跳跃至新的位置，否则不触发跳跃机制。

步骤5更新当前第迭代步数的个体最优值Pibest与全局最优值Pgbest。

步骤6使用式⑸更新惯性权重ω。

步骤7更新迭代步数，判断是否达到最大迭代步长T 或满足预设误差条件，满足条件则输出全局最优粒子位置，即最优惩罚系数C和核参数g的值。未满足返回步骤2。

2 实验与分析

2.1 实验数据处理

实验数据来源于某大气候室运行时的温湿度采集，气候室容积30m3，温度可调范围5～35℃，相对湿度可调范围30%～75%。选取控温水箱、控制露点水箱、露点发生器和外部环境四个数据采集点[19]。如表1，以某一时刻的六个影响因素和历史相对湿度作为模型输入，20 分钟后的气候室相对湿度作为输出，进行模型训练。传感器每秒传输一次数据，气候室开始运行后每分钟选取一组数据作为样本，共采集数据1333组，选取数据的前60%作为训练集，后40%作为测试集来验证预测模型性能。表1 列举了2019 年5 月3 日部分数据资料。

表1 气候室采集温湿度数据

2.2 预测模型构建

采用IPSO-SVM 算法对气候室温湿度数据进行建模预测。算法参数设置如下：种群规模为20，最大迭代步数tmax=200，学习因子c1=0.8，c2=0.7，惩罚系数C∈[0.1,100]，核参数g∈[0.01,10]，IPSO 惯性权重ω∈[0.5,0.9]，PSO 惯性权重ω=1.4。为了进一步体现IPSO 算法在SVM 参数寻优的优势，图2 给出了标准PSO与IPSO算法的适应度曲线对比。

图2 适应度曲线对比

相较于标准PSO 算法，IPSO 算法的适应度在更短的迭代步数达到了稳定，且最优适应度为0.0022，优于标准PSO 的0.0027。可见IPSO 的三种改进策略提高了算法的寻优精度与收敛速度，引入SFLA 跳跃机制提供了算法跳出局部最优的能力，非线性惯性权重ω有效平衡了寻优全期全局搜索与局部搜索能力，基于Tent 混沌映射的初始化种群策略，一定程度上提高了种群的多样性，提高了算法的搜索效率。

2.3 实验结果分析

将IPSO 算法寻优的最优参数组合[C,g]应用于基于SVM 的气候室相对湿度预测建模，GA-SVM 与PSO-SVM 作为对比，测试集533组数据的相对湿度预测效果如图3所示。

图3 相对湿度预测效果对比

本文采用平均绝对误差MAE，均方根误差RMSE和决定系数R2作为模型评价的标准。为了进一步验证本文提出的模型泛化性能，将IPSO-SVM 湿度预测模型与PSO-SVM、GA-SVM 运用于2019 年5 月2 日与5月5日的数据集，图4、图5分别给出这两天的预测的效果图。为了保证实验对比公平性，IPSO与PSO算法参数设置同上，GA 算法种群规模为20，最大迭代步数tmax=200，交叉概率为0.9，采用二进制形式编码。表2给出了三种模型在所有数据集的性能对比。

图4 2019.5.2预测效果对比

图5 2019.5.5预测效果对比

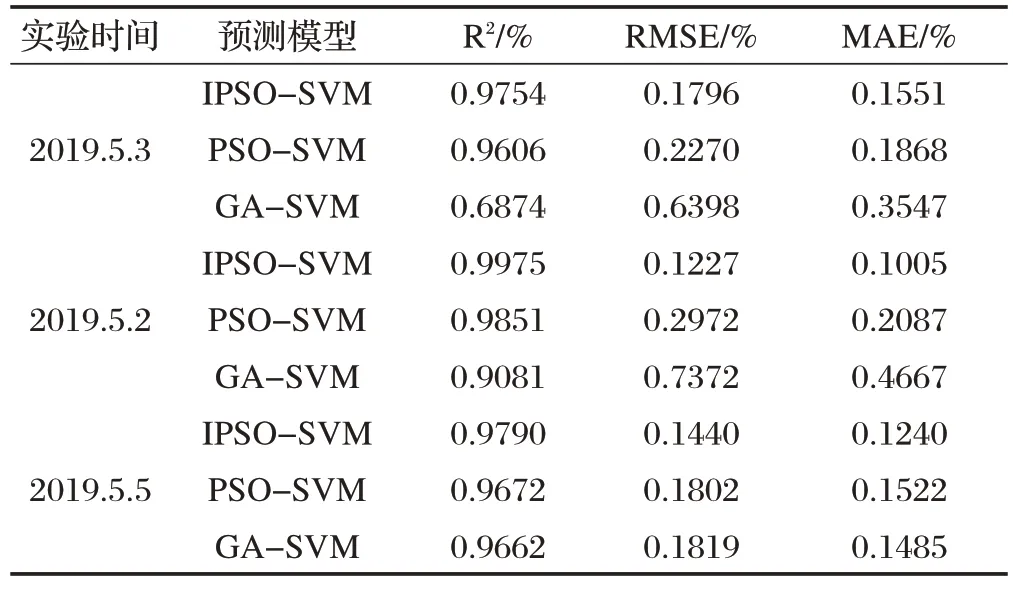
表2 模型性能对比

由表2 可以看出，本文提出的IPSO-SVM 模型在所有数据集中均取得了最优的预测结果，最优的数据拟合度达到了0.9975。对于5 月3 日数据集，IPSOSVM 模型相对于PSO-SVM 和GA-SVM，R2 分别提高 了0.0148、0.2880%，RMSE 分别降低了0.0474、0.4602%，MAE分别降低了0.0317、0.1996%。对于5月2 日数据集，R2 分别提高了0.0124、0.0894%，RMSE分别降低了0.1745、0.6145%，MAE分别降低了0.1092、0.3662%。对于5 月5 日数据集，R2 分别提高了0.0118、0.0128%，RMSE 分别降低了0.0362、0.0379%，MAE分别降低了0.0282、0.0245%。

IPSO-SVM 模型在所有数据集RMSE 的总和为0.4463%，相对于PSO-SVM 和GA-SVM，分别提高了36.64%、71.37%。MAE 的总和为0.3796%，相对于PSO-SVM 和GA-SVM，分别提高了30.69%、61.14%。实验结果表明，针对影响大气候室相对湿度的各个变量之间的强耦合、非线性现状，IPSO-SVM 模型可以精准地预测未来20min的相对湿度，为更及时、精准地控制策略设计提供了有效的参考依据。

3 结论

⑴提出了一种改进的PSO 算法对SVM 进行参数寻优，本文通过采用Tent 映射，初始种群分布更加均匀，引入自适应调节惯性权重，适应度在短时间内达到稳定，并借鉴了SFLA 算法的跳跃机制，取得了比标准PSO 算法更优的适应度值，有效的避免了陷入局部最优的问题。利用IPSO 算法优化SVM 参数，能够更精准的搜寻最优参数组合，提升模型的准确性与稳定性。

⑵将IPSO-SVM 算法应用于大气候室相对湿度的预测。实验结果表明，相较于标准PSO-SVM 和GA-SVM 算法，IPSO-SVM 相对湿度预测模型，拥有最高的预测精度，所有数据集的拟合度均达到了0.97以上，且拥有最小的预测误差。本模型对于大气候室相对湿度控制效果滞后问题具有一定的指导意义。