基于自适应深度神经网络的永磁同步直线电机定位力计算模型*
2023-02-23饶章宇刘春元孙浩宸
饶章宇,刘春元,彭 珍,孙浩宸
(1.浙江理工大学信息学院,浙江 杭州 310018;2.嘉兴学院信息科学与工程学院)
0 引言
永磁同步直线电机(Permanent Magnet Synchronous Linear Motor,PMSLM)具有动态响应快、推力大、效率高等特点,在工业领域[1,2]得到了广泛的应用。但由于PMSLM 的定位力波动降低了系统的可靠性和控制精度,特别是在电机处于低速运行时,还会引起整个装置的共振,危害系统运行的稳定性[3]。
定位力是永磁同步直线电机的一项重要性能指标和固有的特性,其大小和方向与电机运行状态无关[4],准确和快速计算定位力对优化PMSLM 结构和电磁性能具有重要意义。目前计算定位力主要有解析法、有限元法和非参数建模法。解析法[5]是利用已有的电机结构参数和电磁公式计算推导PMSLM 的定位力,解析法为了简化计算,通常都会假设理想的前提条件,结果存在一定误差,计算精度不高;有限元法[6]虽然计算精度高,但计算耗时比较长,效率低;非参数建模法[7-9]通过电机结构参数-定位力的样本库,对样本数据进行回归建模,拟合出电机结构参数和定位力的回归计算模型,常用建模方法有K 最近邻(KNearest Neighbour,KNN)[7]、随机森林(RandomForest,RF)[8]、神经网络[9]等,神经网络建模方法通常有更高的精度,但神经网络结构参数的调整往往需要依赖经验信息和先验知识,建模时需要消耗更多时间成本。
基于上述方法的优缺点,本文提出了一种基于自适应深度神经网络(AdaptiveDeep NeuralNetwork,ADNN)的PMSLM 定位力非参数建模方法。深度神经网络具有更强的泛化能力,其多层网络的特点使其对高维数据具有更好的表达能力,本文在深度神经网络模型的基础上,采用神经网络结构搜索算法搜索最佳模型结构,使神经网络的结构进行自适应,相较于传统的人工调参训练,可以节省大量用于调整深度神经网络结构参数的时间;同时结合一种k折训练方式,能全面利用所有样本,使模型结构更合理。训练ADNN所使用的数据来自有限元分析软件的仿真数据,以确保PMSLM定位力计算模型的高精度和高效率。
1 建立PMSLM定位力样本库
1.1 有限元建模
为了简化计算和提高计算效率,本文利用敏感参数法,重点研究对定位力影响较大的几个参数,包括极弧系数(a)、气隙(g)、背铁厚度(Hb)、永磁体厚度(Hpm)、槽宽(Wslot),PMLSM 的其他主要参数如表1 所示,根据上述参数建立PMLSM 有限元分析模型,其中极弧系数a=τpm/τp。

表1 电机的主要尺寸参数
1.2 获取样本库
根据已建立的有限元分析模型,利用参数化分析,计算得到不同参数的定位力数据,本文的参数范围和步长如表2所示。

表2 研究的结构参数范围和步长
按表2 中的数据,设定求解器时间步长为2ms,按正交组合的方式输出0-200ms 中每组结构参数每个时刻的定位力大小,总共有1200 组实时定位力数据,每组数据有101个定位力数据。
1.3 数据预处理
对于上述原始数据的输入特征,存在特征之间相差过大的情况,由于深度学习模型会在所有样本分布中寻找一个平衡点,这就会导致过小的数据被忽略,难以学习到所有样本特征,所以,需要对数据放缩到相同的分布空间中,本文采用归一化的方法,将样本特征放缩到[0,1]的范围内,对样本标签不做处理。
其中,xi为某一样本的第i个特征为所有样本的第i个特征中的最大值为所有样本的第i个特征中的最小值为该样本归一化处理后的第i个特征。
从归一化处理后的样本数据中去掉与样机实验平台最相近的一组数据,如表3所示,确保模型不会学习到该组数据,用于后续测试,剩余1199 组数据组成样本库。

表3 模型测试使用的电机结构参数
另外,样本库中相邻样本之间仅有一个特征不同,存在特征相似的问题,神经网络是按批进行训练的,当每批的样本特征过于相似时,会使神经网络将相邻的样本之间特征是相似的这一错误信息更新到网络模型中,导致模型收敛速度慢、精度低,所以需要将样本库中的样本顺序随机打乱,确保训练时每批样本特征之间不存在过多联系。
2 定位力计算模型
2.1 ADNN模型原理
深度神经网络是一种模拟人脑神经元进行信息处理的计算系统,其模型构建往往需要依赖经验信息和先验知识,在深度神经网络的基础上使用结构搜索算法构建ADNN 模型,模型由输入层、隐藏层、输出层组成,本文使用全连接网络结构,提前终止法终止训练,验证集误差和决定系数反馈调整模型结构,如图1所示,其中结构搜索算法可以分为搜索空间、搜索策略和性能评估三个维度[10,11]。

图1 ADNN模型结构图
其工作流程如下:
⑴ 给定搜索空间,模型参数初始化。给定ADNN 模型结构的搜索空间,在搜索空间内选定某一结构建立ADNN 模型,并初始化各层的权重参数W和偏置参数b。
⑵正向传播,计算输出结果。选取一定批量的数据作为输入层数据,权重参数Wi与上一层的输出数据yi-1相乘加上偏置量bi得到当前层的输入数据xi,为了使模型能计算非线性问题,输入数据xi需要经过激活函数σ得到当前层的输出数据yi,由此正向传播计算得到最后输出结果y,也即预测结果,其中i为当前神经元所在层数。

⑶反向传播,更新参数。计算预测结果和真实结果的之间的损失LOSS,采用梯度下降法反向传播,更新权重参数Wi和偏置量bi。

其中,ε为学习率。
⑷提前终止法停止学习。选取下一批量的数据重复步骤⑵和⑶,完整训练一遍样本数据算作一次迭代,经过若干次的学习迭代,当满足提前终止法的条件后,完成模型的训练。
⑸反馈调整模型结构。完成模型训练后,评估模型误差和精度,并使用一种搜索策略反馈调整模型结构,寻找搜索空间内性能最优的模型结构。
2.2 模型精度评估
本文使用决定系数R2评估模型的精确性,R2的计算公式如下:

其中,m为样本个数,yi为样本真实结果,yi为模型预测结果为所有样本真实结果的平均值。
当R2越接近1时,则预测值越接近于真实值,模型拟合度越高;当R2越接近0时,则预测值越接近于平均值,说明模型几乎没有预测作用,模型拟合度越低;当R2为负数时,则表明模型预测值的误差比直接使用平均值作为预测值的误差还大,这种情况一般为非线性问题使用了线性模型进行预测会出现,若出现这种情况则说明模型结构存在较大问题。
2.3 定位力计算模型构建
本文ADNN 模型输入层数据为电机结构参数,即输入层节点数为5,输出层数据为电机的一组定位力,即输出层节点数为101,确定搜索空间的隐层数范围为[1,+∞),隐层节点数范围为[5,101];由于模型计算规模较小,可使用顺序搜索策略,算法过程见算法1;在训练ADNN 时使用提前终止法提前停止训练,算法过程见算法2。此外,本文使用一种k 折的训练方式,可以有效利用所有样本,搜索得到最佳模型结构,最后使用所有样本训练最佳模型得到定位力快速计算模型,其构建流程如图2所示。

图2 定位力快速计算模型构建流程图
算法1 顺序搜索算法

算法2 提前终止法

3 模型训练与预测
3.1 传统机器学习预测
本文与两种传统的机器学习算法进行对比,包括KNN算法、RF算法。将预处理后的样本按8:2划分训练集与测试集,各算法主要参数设定如下:
⑴KNN算法中k值设定为5;
⑵RF算法中最大深度设定为不限。
使用训练集数据训练各模型,完成训练后计算测试集均方误差和决定系数。使用三个模型对表3中的结构参数进行定位力预测,与有限元分析软件的输出结果对比分别如图3、图4所示。

图3 KNN模型预测图

图4 RF模型预测图
3.2 ADNN模型预测
3.2.1 模型参数初始化
本文选择LeakyReLU 作为模型的激活函数,解决了ReLU 死神经元的问题,模型的初始学习率设定为0.001,损失函数选择更适合回归任务的均方误差(Mean Square Error,MSE)函数,优化器选择自适应矩 估 计(Adaptive moment estimation,Adam),Adam优化器可动态调整模型学习率,能自然地实现步长退火过程,由于其优秀的性能和精度,被各领域广泛使用[12]。
3.2.2 训练ADNN定位力快速计算模型
将样本库平均分成10 份,按2.3 节中的训练步骤训练ADNN 模型。训练结束后得到10个模型,计算平均隐层数和隐层节点数,得3 个隐层、24 个隐层节点,则最佳模型结构为3 个隐层、24 个隐层节点。用样本库中所有数据训练最佳结构的ADNN 模型即可得到定位力计算模型,该模型的误差和精度可采用k 折交叉验证法进行验证。使用定位力计算模型对表3中的结构参数进行定位力预测,与有限元分析软件的输出结果对比如图5所示。

图5 ADNN模型预测图
3.2.3 k折交叉验证
上一节中使用10折训练方式,直接使用该节的样本分组,进行10 折交叉验证,不同的是不需要再将除测试集外的数据分为训练集和验证集,而是整体作为k 折交叉验证法的训练集。由于上一节所使用的验证集数据为k 折交叉验证法的训练集中的一部分,故不存在数据泄露的问题。训练完成后得到10 个模型的误差和决定系数如图6 所示,计算它们的平均误差和决定系数即为ADNN 定位力快速计算模型的误差和精度。

图6 k折交叉验证法的误差与决定系数
3.3 结果与分析
由3.1 节与3.2 节得到KNN、RF 和ADNN 的误差与精度如图7所示。

图7 KNN、RF、ADNN模型误差和精度对比
ADNN模型精度为99.86%,与KNN、RF的75.15%、97.10%相比,精度分别提高32.88%和2.84%。人工调参时,逐一对模型分析、调整与训练,建立高精度模型大约需耗费100min;ADNN 完整自适应调整过程仅耗费14min50s,时间消耗减少85.17%。
4 实验验证
为了验证ADNN 定位力快速计算模型能有效计算永磁直线电机的定位力,用MTS100kN 万能试验机进行试验。样机实验平台所使用的永磁直线电机结构参数如表6 所示,使用MTS100kN 万能试验机以0.001m/s 的速度带动永磁直线电机工作,如图8 所示。电机初级的质量为M,向上移动时读取力传感器的数据FU(t),向下移动时读取力传感器的数据FD(t),经过计算得到其定位力Fd(t)。


表6 实验平台使用的电机结构参数

图8 样机实验平台示意图
使用ADNN 定位力快速计算模型计算表6参数的定位力,与样机实验平台测量的数据对比如图9所示。ADNN 模型计算结果与实验结果基本一致,说明ADNN 定位力快速计算模型是有效的,其中存在一些偏差的主要原因是训练模型的样本数据由软件仿真得到,没有考虑损耗和摩擦等因素。
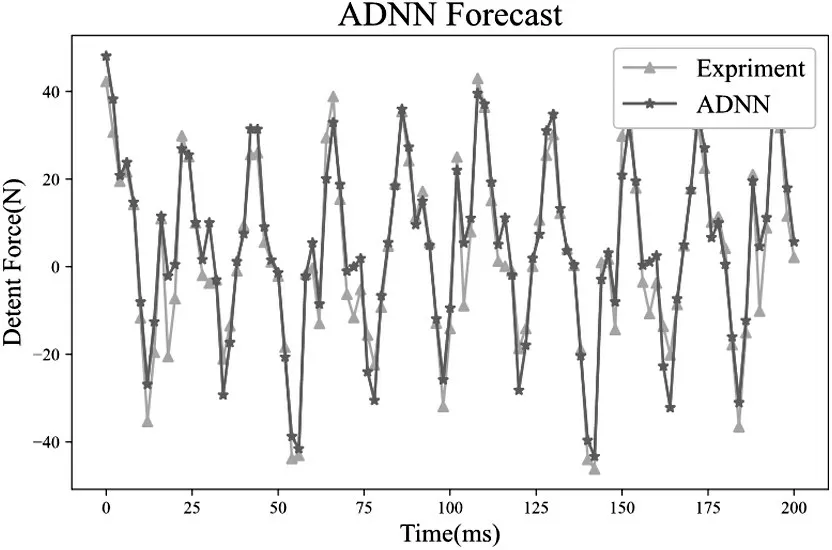
图9 ADNN预测数据与实验数据对比
5 结束语
本文提出了一种结构自适应的ADNN 模型,通过提前终止法和结构搜索算法能快速找到最佳模型,k折训练方式能有效利用所有样本,然后使用k 折交叉验证法计算其精度,并和K最近邻、随机森林的精度进行对比,最后使用样机平台验证模型的有效性。实验结果表明,基于ADNN 的定位力计算模型具有良好的精度和性能,解决了传统机器学习算法精度不足的问题,且ADNN 的结构自适应特性相比人工调参的深度神经网络模型,建模效率显著提高。未来考虑引入智能算法改进本文的神经网络结构搜索策略,诸如遗传算法、粒子群优化算法等,进一步提高效率和准确性。
