亚临界雷诺数圆柱涡致振动的实验研究
2023-02-22张伟伟寇家庆
吕 振,张伟伟,寇家庆
(西北工业大学 航空学院,西安 710072)
0 引 言
圆柱绕流是一个经典的流体力学问题。众所周知,静止圆柱绕流在雷诺数Recr≈ 47时开始变得不稳定,出现周期性的旋涡脱落[1-2]。但是当圆柱处于强迫运动或弹性支撑状态时,其临界雷诺数可能会进一步降低[3-4]。其中,弹性支撑的圆柱在一定来流条件下会发生振动,且其尾迹中会产生周期性涡脱,这一现象被称为涡致振动[3,5-6]。
Bufoni[7]在风洞实验中研究了强迫运动圆柱在低雷诺数下的尾涡演化规律,发现圆柱最低涡脱雷诺数可以降低至25。Cossu和Morino[4]通过全局线性稳定性分析方法对亚临界雷诺数下的涡致振动开展了研究,发现在高质量比时,弹性支撑圆柱的临界雷诺数可以降低到静止圆柱的一半。随后,Mittal和Singh[8]在数值仿真环境下,也采用全局稳定性分析方法研究了不同亚临界雷诺数下圆柱发生涡致振动的折减速度范围,发现圆柱涡致振动存在的最低雷诺数为20。同时,他们在发生亚临界雷诺数涡致振动的所有状态下都观测到了“锁频”现象。进一步地,Zhang等[9-10]基于线性稳定性分析方法研究了亚临界雷诺数时圆柱在横向和流向自由度上的涡致振动特性,发现当同时释放这两个自由度时,圆柱发生涡致振动的雷诺数可进一步降低到18。Kou等[11]采用动态模态分解(DMD)获取了不同亚临界雷诺数下圆柱绕流的流动模态。他们发现,与超临界雷诺数圆柱绕流不同,亚临界雷诺数圆柱绕流的流动模态是稳定,且其强度随着雷诺数降低而降低,并最终在雷诺数小于18时消失。这一雷诺数与圆柱涡致振动存在的最低雷诺数相一致,因而Kou等认为亚稳定流动模态的消失是涡致振动无法在Re<18时存在的直接原因。最近,Bourguet[12]通过直接数值模拟的方法研究了三维柔性柱体在亚临界雷诺数下的涡致振动特性,发现其发生涡致振动的最低雷诺数为20,与二维圆柱一致。另外,他们发现柔性柱体的高阶结构模态也会与流动发生耦合,诱发高频的涡致振动。
虽然上述的数值模拟工作对亚临界雷诺数涡致振动问题展开了较为全面和深入的研究,但是到目前为止研究者还未能在实验中证实亚临界雷诺数涡致振动的存在。在公开发表的文献中,所有涡致振动实验[3,13-15]的雷诺数都大于100。其主要有以下两个原因:1)在一般的风洞和水洞中很难实现很低流速的流动;2)亚临界雷诺数实验的实验模型尺寸小,弹性支撑机构的设计难度大。针对以上问题,本文设计并开展了低雷诺数实验,研究了结构支撑频率和雷诺数对圆柱涡致振动的影响,分析了亚临界雷诺数涡致振动的存在性。
1 实验设计
1.1 旋转水槽
本文试验所需的雷诺数很低,如何实现足够低速(几厘米每秒量级)的稳定流动是本文研究的重点和难点。因传统循环水槽/水洞中几乎不可能实现如此低速的流动,本文借鉴地球物理学研究中的圆形水槽[16-17]研发了如图1所示的旋转水槽[18]。该旋转水槽由两个一端粘贴在圆形底板上的同心圆筒所组成,两个圆筒的直径分别为500 mm和380 mm。圆形底板在其圆心处与一个步进电机的轴相连,因而整个水槽可以在步进电机的驱动下在0到0.306 rad/s(对应水槽中央处速度为0~7.0 cm/s)的角速度范围内转动。实验中所采用的步进电机转速控制精度很高,从而保证了水槽可以按设定的角速度平稳转动。在开展实验前,首先需要在两个圆筒围成的水槽中注入一定高度的水;然后,启动步进电机使旋转水槽以一定的转速转动。约10 min后,在黏性力的作用下,水槽中水的流速就会和水槽转动速度保持一致,形成稳定的低速流动。在本文实验中,为了消除温度对水黏性系数的影响,将水槽中水的温度严格控制在20±0.1℃。

图1 实验装置Fig. 1 Setup of experiments
为了评估旋转水槽中流场的品质,本文采用2DPIV测量了不同水平截面处的流场速度分布。图1(c)给出了水槽中坐标系的定义,其中坐标系原点位于水槽中央,水流方向为x轴,垂直于水流方向的横向为y轴。图2给出了转速Ω =0.102 rad/s时,水槽中间区域在典型水平截面上的瞬时速度分布,可以看出其流场的均匀性较好。需要注意的是,图2中不同y轴占位处到水槽旋转轴的距离不同,因而流速会沿着y轴正方向逐渐增加。进一步地,图3给出了该状态下的湍流度分布云图,可以看出水槽中区域整体湍流度水平在1%左右,与一些低速水洞的湍流度相当[19],满足本文实验需求。另外,还需要考察旋转效应对流动的影响。在地球物理学中,一般用Rossy数[20-21]来度量旋转效应对流动的影响,其定义式为Ro = U/(2ωL)= R/(4d),其中R为模型到水槽旋转轴的距离,d为模型特征长度。Ro数越小,旋转效应对流动的影响就越显著。一般地,当Ro大于1时,可以忽略旋转效应对流动的影响。在本文实验中,Ro为58.75,远大于1,说明旋转效应对流动的影响很弱,可以将其忽略。
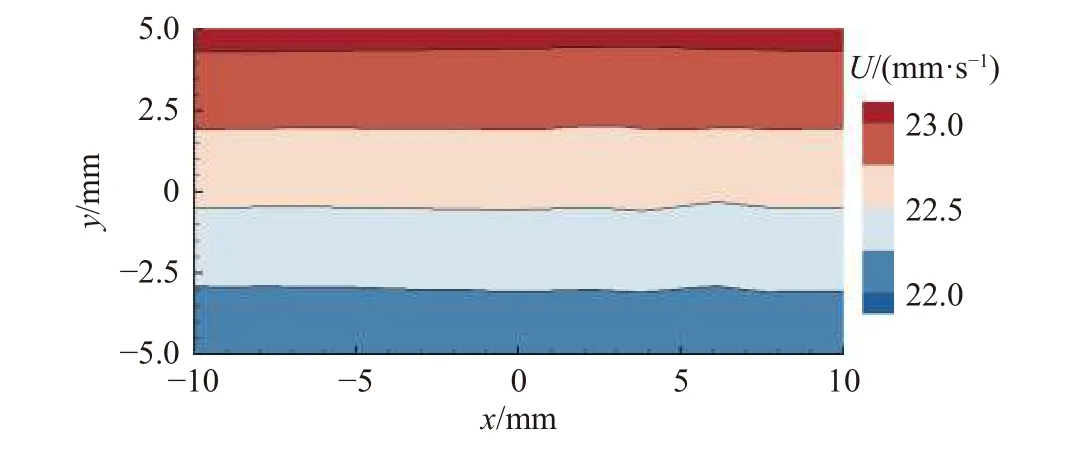
图2 转速Ω = 0.102 rad/s 时,水槽横截面速度云图Fig. 2 Velocity contours in a cross-section of the channel rotating at a speed Ω = 0.102 rad/s
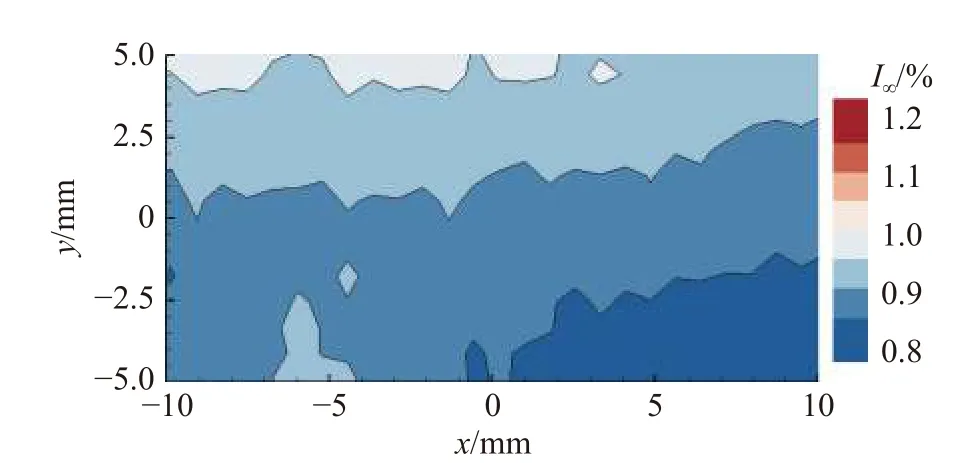
图3 转速Ω = 0.102 rad/s 时,水槽横截面湍流度分布Fig. 3 Turbulence intensity in a cross-section of the channel rotating at a speed Ω = 0.102 rad/s
1.2 实验模型及测量方法
实验中使用的模型为直径d= 1 mm、长度L=100 mm的铝质圆柱。如图1所示,圆柱的顶端由两个平行的弹性PVC片支撑,使得圆柱只能沿垂直于来流方向做横向振动,消除了圆柱在其他方向的自由度。实验中通过调节PVC片的长度和宽度来改变圆柱的支撑频率。为了消除重力对圆柱涡致振动响应的影响,实验中将圆柱竖直地安装于水槽中,其末端距离水槽底面高度为2 mm,浸水高度l =90 mm。
如图1所示,在实验中使用布置于圆柱正下方的高速相机测量圆柱振动位移,其拍摄帧率为100帧/s,对振动位移测量的分辨率为1.4 μm。同时,采用2维时间解析的PIV测量圆柱尾迹区流场。在水槽中布撒密度为1.03 g/mm3、直径约20 μm的聚酰胺树脂颗粒作为示踪粒子;而后,采用一台功率为5 W的连续式半导体激光器在距离水槽底面45 mm的平面上产生厚度约1 mm的片光照亮待测流场区域。最后,使用Pointgrey GS3-U3-23S6M-C型高速相机采集粒子流动的图像,其分辨率为1 920×1 200。 每个实验状态下,PIV系统以100 Hz的频率连续记录了9 000张流场快照。基于开源的PIVlab v2.31软件对粒子图像进行后处理,采用的询问窗口大小为24 pixel×24 pixel,重叠率为50%,空间矢量分辨率为0.385 mm,对速度场测量的不确定度小于2%。
在地面实验中,给圆柱施加横向的脉冲激励并测量其在空气中的位移衰减响应。通过对位移衰减响应进行频谱分析和时域减幅率计算,分别得到圆柱的支撑频率fn和系统的阻尼比ζ。地面实验中测得不同支撑频率下系统的阻尼比在0.006至0.008之间变化。2021年1月份,在旋转水槽分别开展了固定支撑频率变来流速度和固定来流速度变支撑频率的两组实验[18],研究了雷诺数和支撑频率对圆柱涡致振动特性的影响。
2 实验结果及分析
2.1 静止圆柱
为了验证实验设计的可靠性,本文首先研究了静止圆柱临界雷诺数的大小。图4给出了不同雷诺数下圆柱尾迹的涡量云图。如图4(a、b)所示,当雷诺数小于47时,可以清晰地看出圆柱后有两条互不交叉的剪切层,这说明此时圆柱后没有产生涡脱,流动没有发生失稳。而当雷诺数大于47时,如图4(c、d)所示,圆柱后开始产生交替脱落的旋涡,说明流动发生了失稳。由此可见,本实验中圆柱的临界雷诺数是47,与经典实验和直接数值模拟结果[1-2,22]一致。进一步地,图5给出了不同雷诺数下圆柱绕流的斯特劳哈尔数。可以看出,本文实验结果与均匀流中经典实验结果[23-24]吻合很好,这充分说明了本文实验平台的可靠性和测试精度。
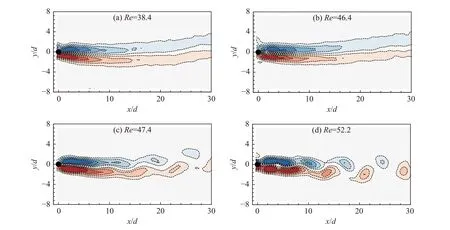
图4 不同雷诺数下静止圆柱的尾涡云图Fig. 4 Wakes of a fixed cylinder at various Reynolds numbers

图5 不同雷诺数下圆柱绕流的斯特劳哈尔数Fig. 5 Strouhal number for flow around a cylinder at various Reynolds numbers
2.2 弹性支撑圆柱
第一组实验研究了支撑频率fn =1.92 Hz的圆柱在不同来流速度下的涡致振动响应。该组实验中支撑系统的阻尼比为ζ =0.006 6,质量比为m*= 4.87,其中质量比的定义式为:m* =4m/(πρld2)。式中,m为包含模型和支撑系统在内所有运动部件的等效质量,ρ为水的密度,l为圆柱浸没在水中的长度,d为圆柱的直径。
一般采用无量纲位移和无量纲振动频率来描述涡致振动的响应,其定义式分别为:h* = h/d和F* = f/fn。其中,h为圆柱的有量纲位移,f为圆柱的有量纲振动频率。另外,还需要对来流速度予以无量纲化得到折减速度,其定义式为:U* = U/(fnd),其中U为来流速度。需要注意的是,在本组实验中,改变来流速度会同时改变雷诺数和折减速度。
图6(a)展示了弹性支撑圆柱的无量纲位移和振动频率随折减速度的变化曲线。从图中可以看出U*<6.06时,圆柱振动的振幅基本为0;而在U*=6.06时,圆柱突然开始大幅振动,且随着U*的增加,振幅急剧增加,并在U*= 6.76时达到峰值;当U*>6.76时,振幅随着折减风速增加而逐渐减小。图6(b)给出了圆柱发生涡致振动时,其无量纲振动频率随折减风速变化的曲线。可以看出,无量纲振动频率始终在1附近。这种结构振动频率跟随结构固有频率的现象被称为“锁频”,其存在于整个低雷诺数圆柱涡致振动过程中。这一发现与Mittal、Singh等[8]的数值仿真结果相一致。

图6 不同折减速度下的涡致振动振幅和频率Fig. 6 Amplitude and frequency responses of VIV at various reduced velocities
进一步地,图7给出了四个典型折减速度下弹性支撑圆柱的尾涡云图。当U*= 6.06 (Re= 37.6)时,圆柱没有发生振动,在尾迹中也没有发现涡脱。当U*= 6.12(Re= 38.0)和U*= 6.76(Re= 41.9)时,圆柱发生了周期性振动。虽然此时圆柱的雷诺数小于47,但仍然可以在其尾迹中观测到卡门涡街。当U*=10.23时,圆柱振动的振幅变得很小,在尾迹中仍然观测到了清晰的卡门涡街。这是因为此时圆柱的雷诺数Re= 72.1,大于静止圆柱的临界涡脱雷诺数。另外,圆柱发生涡致振动时,其尾涡脱落频率始终与圆柱振动频率保持一致,且都在圆柱支撑频率附近。这些实验观测到的“锁频”特性与数值模拟得出的结论完全相同。

图7 典型折减速度下,圆柱的尾涡云图(左)及时域位移响应(右)Fig. 7 Wake (left) and displacement responses (right) of the elastically supported cylinder at typical reduced speeds
值得注意的是,U*<7.58时,圆柱的雷诺数小于47,但是涡致振动现象仍然存在,证明了Mittal[8]和Zhang[9]在数值仿真环境下发现的亚临界雷诺数涡致振动现象是真实存在的。另外,在亚临界雷诺数涡致振动的过程中伴随着周期性的旋涡脱落,说明弹性支撑会降低圆柱绕流的稳定性,使得流动在低于47的雷诺数下提前失稳。该结论与我们先前采用线性稳定性分析方法得出的结果[9-10]一致。
2.3 圆柱涡致振动的最低雷诺数
为了进一步研究圆柱涡致振动存在的最低雷诺数,本文分别在Re= 20、23、30和40四个不同的亚临界雷诺数下开展实验。每个雷诺数下,来流速度是恒定的,通过改变圆柱的支撑频率来改变折减速度。因支撑频率的改变是通过改变PVC片长度来实现的,故PVC片的附加质量会随着支撑频率的增加而降低,使得模型的质量比在7.73~9.19范围内变化。另外,PVC片长度增加时,支撑系统的阻尼比也会变小,使得实验中系统阻尼比在0.006~0.008范围内变化。
图8(a)给出了四个不同雷诺数下圆柱涡致振动无量纲振幅随折减速度的变化。可以看出,Re= 20时圆柱在各个折减速度下的振动振幅都基本为0,说明此时并没有发生涡致振动;而当Re>20时,在一定的折减速度范围内圆柱会发生极限环振动,说明此时发生了涡致振动。另外,随着雷诺数的增加,发生涡致振动的折减速度范围和涡致振动最大振幅会逐渐增大。以上实验结果表明,亚临界雷诺数下,圆柱横向涡致振动存在的最低雷诺数为23,与Mittal等在数值模拟中得出的Recr= 20接近。
另外,图8中黑色实线给出了李新涛[22]在Re=40、m*= 10状态下通过直接数值模拟方法得出的圆柱涡致振动振幅及频率响应。数值仿真得出的涡致振动退出边界和本文在Re= 40时的实验结果吻合较好,而涡致振动始发边界及最大振幅与本文实验结果有一定差别。李新涛[22]和Blevins[25]在超临界雷诺数下的圆柱涡致振动中发现结构阻尼会显著影响涡致振动发生的折减速度区间及其振动幅值。而本文实验存在一定的结构阻尼,但李新涛的数值模拟中结构阻尼为0。这种结构阻尼的不同可能直接导致了实验结果与直接数值模拟结果的差别。
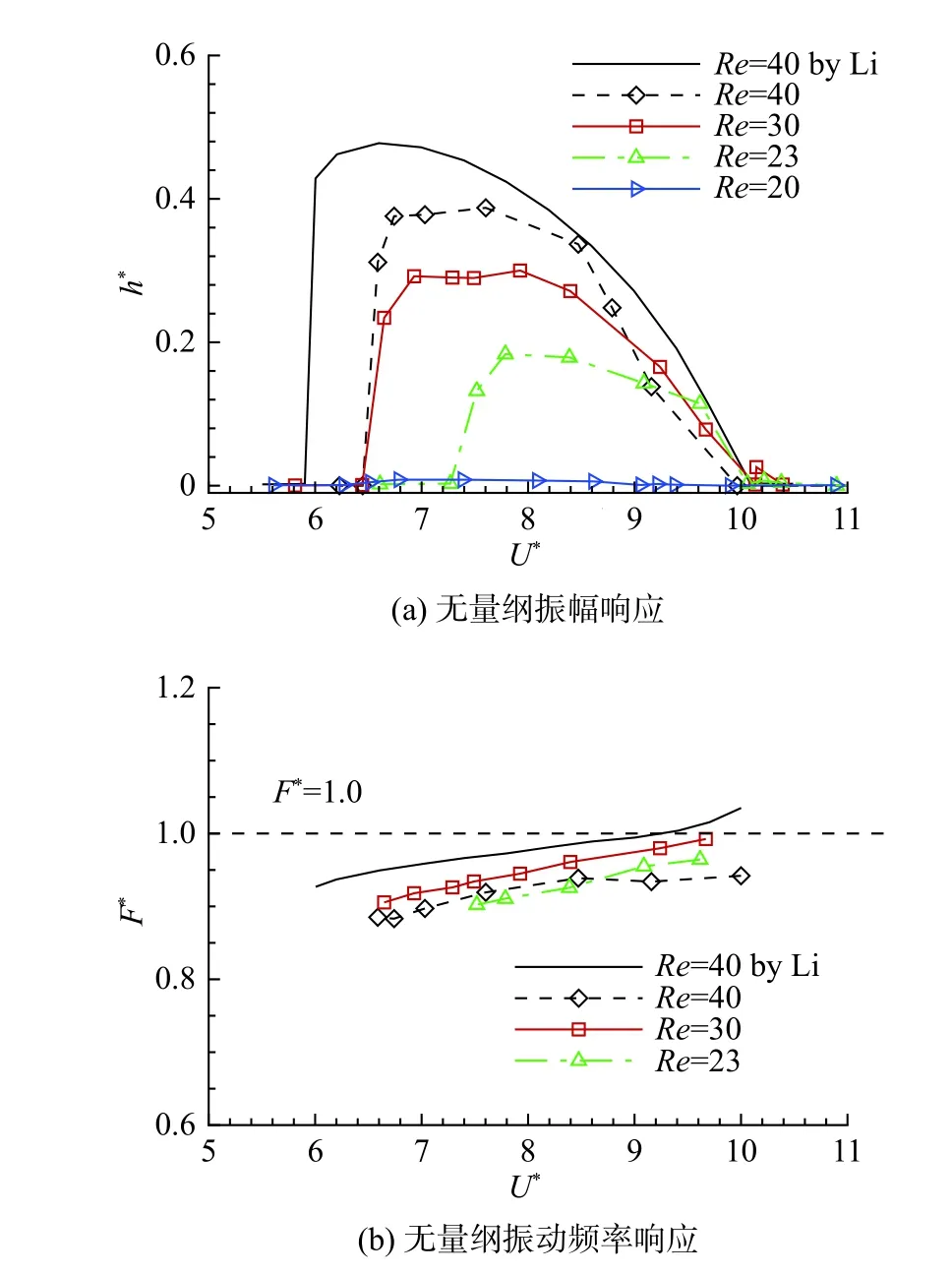
图8 不同雷诺数下,涡致振动振幅和频率响应的对比Fig. 8 Comparison of amplitude and frequency responses of VIV at different Reynolds numbers
图8(b)给出了四个不同雷诺数下无量纲结构振动频率随折减风速的变化曲线。值得注意的是:不同雷诺数下,发生涡致振动时的无量纲结构振动频率都在1附近。这说明“锁频”现象在亚临界涡致振动中持续存在,与Mittal[8]和李新涛[22]的数值仿真结果一致。
3 结 论
本文针对数值模拟中所发现的亚临界雷诺数涡致振动问题开展了水槽实验,分别研究了不同结构支撑频率和雷诺数下圆柱涡致振动的响应,在实验中证实了亚临界雷诺数涡致振动现象的存在。研究的主要结论如下:
1)为了实现实验所需的低雷诺数流动,本文研发了旋转水槽,其可产生流速范围为0~7.0 cm/s的稳定流动,且湍流度水平在1%左右,其对低雷诺数下的相关实验研究有重要的参考价值。
2)实验发现圆柱涡致振动可在雷诺数低于47的亚临界雷诺数下存在,且其发生的折减速度区间和最大振幅会随着雷诺数的降低而减小。另外,实验中圆柱涡致振动存在的最低雷诺数为23,与Mittal等[8]数值仿真结果接近。
3)发生亚临界雷诺数涡致振动时,圆柱下游会产生频率与圆柱振动频率相一致的周期性涡脱。这说明弹性支撑会使得流动的稳定性降低,从而使得流动在雷诺数小于47时提前失稳,证实了我们先前采用线性稳定性分析方法得出的结论[9-10]。
本研究通过实验证实了亚临界雷诺数涡致振动的存在,并获取了其存在的最低雷诺数,但并未能解释其诱发机理。故后续工作将基于实验数据构建涡致振动的物理模型,对其诱发机理进行剖析。
