华中科技大学Φ 0.5 m马赫6 Ludwieg管风洞设计与流场初步校测
2023-02-22黄冉冉张成键李创创徐冰慧许多龙袁先旭
黄冉冉,张成键,李创创,徐冰慧,许多龙,袁先旭,吴 杰,*
(1. 华中科技大学 航空航天学院,武汉 430074;2. 中国空气动力研究与发展中心,绵阳 621000)
0 引 言
2022年2月,美国国家科学技术委员会(NSTC)发布了新一版《关键和新兴技术清单》(critical and emerging technologies,CETs)[1]。该 清 单 以 美 国2020年《关键和新兴技术国家战略》为基础,对其中的关键和新兴技术领域列表作了更新和调整,并具体列出了各领域内的核心技术子领域清单。在高超声速技术领域,空气动力学和控制、推进、材料、探测/追踪/识别、防御5个方向被定义为了关键和新兴技术。其中,高超声速空气动力学研究与控制技术的发展水平直接决定了下一代先进高超声速飞行器精细化设计能力,但是目前在高超声速空气动力学方向还存在诸多难题,如高超声速边界层转捩[2]、激波/边界层干扰[3]、高超声速湍流[4]等。
为了深入认识以上关键高超声速气动问题,为高超声速飞行器精细化设计提供理论支撑,需要持续强化高超声速空气动力学机理研究。目前开展高超声速空气动力学的常用手段包括飞行试验、数值模拟和地面风洞实验。其中飞行试验的结果最为准确,但试验成本高,且测量流场物理量有限;数值模拟所需成本相对较低,且可获取全局物理场,但对部分物理机理尚不清晰的流动现象缺少可靠的模型;相比之下,风洞实验可以以较低的成本直观反映高超声速流动的物理机理。但是,常规高超声速风洞为维持较长的运行时间,需要较大的储气罐和真空罐,这大大提高平台的建设和运行成本,运行效率也相对较低。在不同类型高超声速风洞中,Ludwieg管风洞设计[5]近些年在欧美得到了广泛应用。根据美国空军研究院Cummings等2012年的统计,全世界在使用的Ludwieg管风洞大概有18座[6]。近期,美国圣母大学、美国空军研究院分别建成了Φ0.6米级和Φ0.5 m Ludwieg管风洞[7-8],我国华中科技大学建成了基于快开阀主控的Φ0.25 m马赫数6 Ludwieg管风洞[9]。与此同时,美国普渡大学以及圣母大学正在研发基于Ludwieg管风洞设计的静音风洞,国内部分科研机构和院校也在发展基于Ludwieg管的先进风洞。相比常规高超声速风洞,Ludwieg管式高超声速风洞具备以下几个优点:1)基于中心膨胀波原理产生来流的总温和总压确保了风洞运行过程中的雷诺数处于定常状态,流场稳定性与重复性好;2)Ludwieg管风洞构成部件少,沿程总压损失低,可模拟更高的来流雷诺数;3)在相同雷诺数下,Ludwieg管风洞建设成本更低,一座实验段口径为0.5 m的Ludwieg管高超声速风洞的建造成本约为1百万美元,其每车次运行费用也仅需数美元[10];4)运行Ludwieg管风洞仅需1名实验人员即可,操作简单,每天运行车次可高达60车次。得益于上述优点,Ludwieg管风洞极其适合用于高超声速空气动力学基础实验研究,如边界层转捩、湍流等问题。然而,我国目前Ludwieg管式高超声速风洞并不多见,对该风洞的运行原理也缺乏深入认识。此外,虽然大口径Ludwieg管风洞与小口径Ludwieg管运行原理相同,但是由于其实验段口径更大,在设计和运行过程中存在更多问题,如:快开阀门尺寸增加进而影响下游流场,快开阀门重量增加导致短时启闭困难,储气段直径增加导致加热不均匀等。如若上述问题得以解决,更大口径的路德维希管风洞可容纳更大比例的模型,且自由来流流场质量也会有所提升,可更好地服务于高超声速空气动力学关键气动问题的实验研究。
针对国内低成本、大口径科研型高超声速风洞短缺现状,本研究团队基于前期自主设计Φ0.25 m快开阀主控式高超声速Ludwieg管风洞的经验和技术储备(图1)[11-12],开展了马赫数6Φ0.5 m口径Ludwieg管风洞气动设计与流场的初步校测。本文的内容组织如下:第一部分介绍基于Ludwieg管式高超声速风洞设计的气动原理;第二部分对Φ0.5 m快开阀式高超声速Ludwieg管风洞开展了关键指标的总体设计;第三部分,基于开源CFD程序SU2对兼顾最优Laval喷管流场品质和结构设计成本的Ludwieg管风洞喷管段进行了数值优化;之后,对该新建的高超声速风洞进行了静态和动态流场的初步校测;最后,对该风洞的设计进行总结,并对其潜在的应用进行展望。相比于之前的Φ0.25 m Ludwieg管风洞设计与校测[9],本文在数值方面重点放在膨胀波系在整个风洞运行过程中的强度以及位置变化,并评估了膨胀波的非定常特征,在实验方面还进一步采用了多种方法对风洞的流场品质进行了校测,验证了对于大口径德维希管风洞,采用弯折长直储气段设计的快开阀主控型Ludwieg管设计依旧可行,研究方式更加完善。

图1 华中科技大学Φ 0.25 m快开阀主控式马赫6高超声速Ludwieg管风洞Fig. 1 HUST Φ 0.25 m Mach 6 hypersonic Ludwieg tube windtunnel controlled by fast-opening valves
1 Ludwieg管运行原理
高超声速Ludwieg管风洞通常由储气段、快开阀、Laval喷管、实验段、扩张段和真空罐构成[5],其运行原理如图2所示。风洞启动前快开阀关闭,阀门上游为高压储气段,下游均为真空状态。快开阀开启后风洞启动,位于储气段的高压气流会向低压区流动,储气段的右端与快开阀连接处将产生一系列膨胀波(图2 CD段),并以当地声速向储气段上游传播;膨胀波到达储气段尾端后发生反射(AB段)并返回下游,当反射波到达阀门附近时(EF段),阀门关闭,风洞结束运行。在膨胀波系向左行进与反射过程中,Laval喷管入口处可产生稳定的来流总温和总压,气流在Laval喷管内加速到设计马赫数,并维持高超声速流动,直至反射膨胀波到达阀门附近。
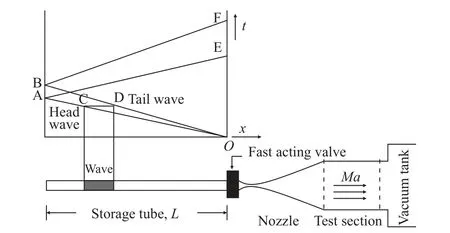
图2 Ludwieg管风洞的运行原理图[5]Fig. 2 Schematic diagram of the operation of Ludwieg tube wind tunnel[5]
风洞启动前后储气段内的流场状态可以通过简单波理论[13]计算:

式中下标0和1分别表示储气段在风洞未启动和启动时的状态,γ为理想气体的比热,c为当地声速,当地流速u1可以通过下式获得:

Ma1为Ludwieg管风洞的启动马赫数,由储气段和喷管喉道的面积比决定[14]:

2 Ludwieg管风洞总体设计
综合考虑实验平台的用途定位与实验室场地,该Ludwieg管定位设计马赫数为6,风洞有效运行时间达100 ms以上,实验段的出口直径为0.5 m,可模拟最大单位雷诺数达3 × 107/m。
2.1 储气段设计
储气段位于Ludwieg管风洞上半段,是Ludwieg管风洞区别于其他高超声速风洞的重要部分,其主要为Ludwieg管风洞运行提供稳定的驻点压力和温度,并确保风洞的有效运行时间。根据本设计要求,为了确保足够的非定常流动现象采样时间,有效运行时间t需大于100 ms;风洞有效运行时间可通过膨胀波系在储气段内往返一次的时间估算:

式中L为储气段总长度。为了防止驻点流动经Laval喷管等熵膨胀出现气体冷凝现象,采取电加热方式对储气段部分进行加热,在马赫数6流动下风洞的驻点温度需要高于430 K,因此可得储气段的长度至少为20.79 m。
此外,为了保证实验段的流场品质,储气段的启动马赫数一般取较小值,根据Radespiel等的经验,要求储气段内启动马赫数小于0.058[10]。以马赫数6 Laval喷管的收缩段设计为基准,根据公式(3),可确定储气段的内径需要大于0.217 m。
受限于实验场地的空间大小,该Ludwieg管风洞储气段采用了两段式直管结合单段半圆式弯管设计,根据前期设计经验,本弯管部分的中心轴线直径定为1 m。
Ludwieg管储气段启动前后总压和总温的关系可由下式计算得到:
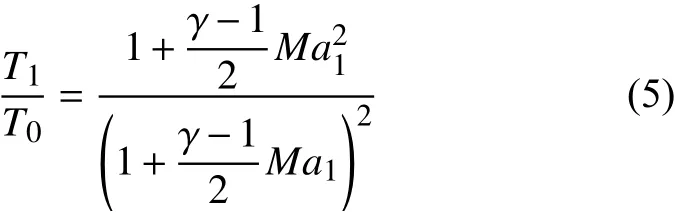

因此,可以通过调节储气段的总温和总压进行来流雷诺数的设置。通常,为了控制模型的壁温比,往往是在总温不变的情况下,通过控制储气段的总压实现来流雷诺数的调控。如在总温为430 K的情况下,如果将储气段的总压调至 3 × 106Pa,自由来流的单位雷诺数约为3 × 107/m。
2.2 快开阀设计
快开阀位于高压储气段和低压部件之间,主要控制Ludwieg管平台运行过程的开启与关闭。基于Ludwieg管运行原理,本实验平台的总运行时间约100 ms,国内外通径超过百毫米通径的商用快开阀响应时间通常达到数秒,无法捕捉本实验平台的有效运行时间。针对该问题,国际上通行的办法有破膜式和快开阀式两种。破膜式简单方便,但是更换膜片麻烦,且每次破膜后储气段内的高温高压气体均释放到真空罐,重新加载压力与抽空真空罐的气体耗时长,导致实验平台的运行效率较低。以普渡大学的马赫数6静音实验平台为例,该Ludwieg管每天运行不到10车次。第二种方式是由哥廷根德国宇航院研发的快开阀系统,可有效控制每车次从储气段流出的气体质量,实现了Ludwieg管风洞的高效运行。以德国布伦瑞克工业大学的马赫数6 Ludwieg管为例,其有效运行车次每天可达到60车次以上。由于其每车次释放的气体流量可控,实验平台的建设与运行成本大幅下降。鉴于以上因素,本项目采用该快开阀式的设计方案,如图3所示。其运行原理如下:快开阀位于储气段与Laval喷管之间,整体设计为梭形,以尽量减小流场的扰动;风洞运行前A、B区均为高压气体,C区为真空状态,阀芯受到压差作用与喷管收缩段紧密贴合;活塞的行程L= 66 mm;当排空A区内的高压气体时,由于受到B区高压气体的影响,阀芯向左运动,阀门开启,风洞启动。以常规雷诺数1 × 107/m的储气段工况为例,阀门所受压差P约为9 × 105Pa,根据式(7),代入活塞的质量m=1.4 kg、轴心面截面积S=0.012 2 m2,活塞受到压力驱动后的加速度a约为7 843 m/s2,后根据式(8)估算活塞完全开启时间t约为0.004 1 s,即4 ms左右。当到达风洞所需运行时间后,重新在A区冲入高压气体,阀芯再次受到压差作用向右运动恢复啮合状态,风洞运行结束。

图3 快速开启阀门示意图Fig. 3 Schematic diagram of quick-opening valve

2.3 Laval喷管设计
Laval喷管位于快速开启阀门下游,通常由收缩段、喉道和扩张段组成,决定了风洞实验段自由来流的流场品质。为保证快开阀与收缩段的啮合,以隔离上下游高低压气体,本项目的喷管收缩段采用入口改进的Witoszynski曲线设计;为保证上游亚声速到下游超声速流动的均匀过渡,喷管喉道位置采用圆弧设计[15];喷管扩张段在传统Sivells方法[16]生成的曲线中间添加了一段线性段以抑制喷管壁面Görtler涡的发展。通过调整收缩段与扩张段的长度,综合考虑流场均匀性与喷管的总长度,最终确定的Laval喷管型线如图4所示。

图4 Laval喷管型线Fig. 4 Laval nozzle profile
2.4 实验段及扩张段设计
试验段位于Laval喷管和扩张段之间,是开展实验测量与观测的场所,需满足不同类型模型的实验需求。考虑到本实验平台基础研究的定位以及精细化空间点测量的需求,采用了闭口式的实验段设计方式,如图5所示。为了便于对实验模型进行光学成像观察,试验段采用左、右以及上侧开窗,每个窗口均采用Φ350 mm的开口。在试验段的下端采用开口式箱体,便于安装电动支撑系统,为后期远程调控实验模型位置提供空间。
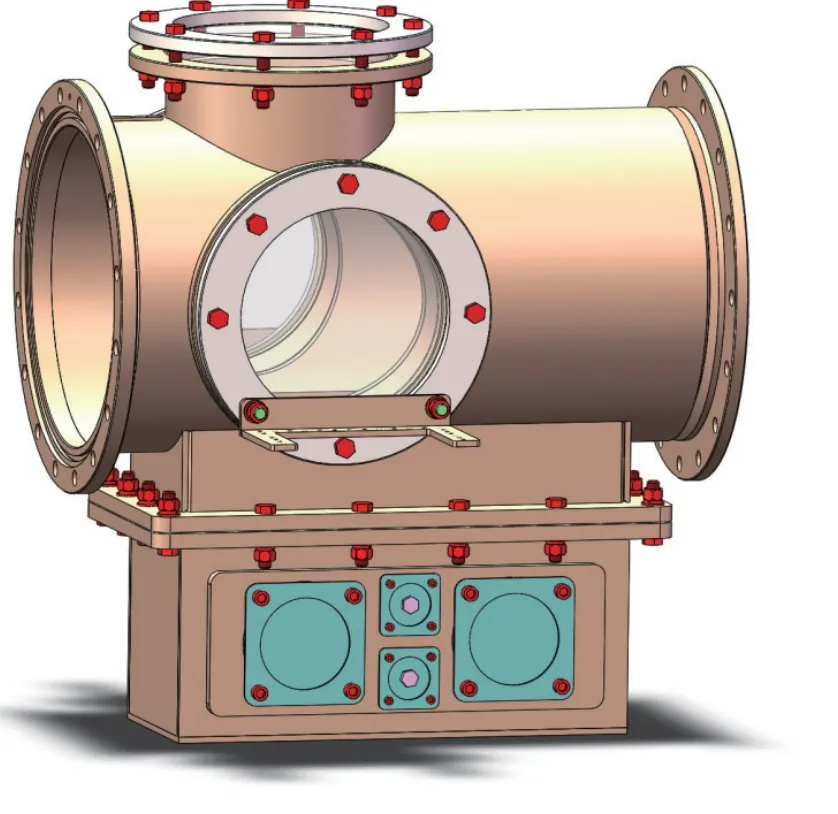
图5 实验段模型图Fig. 5 3D model of the test section
在试验段下游为扩张段(图6),该处直接采用等值段设计,以防止流场的堵塞。在试验段与扩张段之间通过法兰连接,设计有尾部支撑,用于承载较大载荷工况。由于扩张段中心轴有尾部支撑套筒,一定程度上起到了恢复压力的作用。

图6 扩张段模型图Fig. 6 3D model of the expansion section
2.5 真空罐设计
真空罐位于扩张段下游,通过真空泵抽成真空环境,以形成快开阀上下游的高低压差。为了确保风洞单个周期的有效运行时间,真空罐的容积需要进行精确估算。以本设计为例,考虑在最大总压工况p01=3 × 106Pa以及总温T0= 430 K条件下,风洞有效运行时间t= 100 ms,真空罐的最小容积可通过下式计算:

其中:mt=m×t,为风洞有效运行的整个过程中喷管内部流过的气流质量,m可通过等熵关系式计算出的喷管出口处流体密度和速度相乘得到,在最高总压设计工况下为21.49 kg;由于真空罐体内气体初始密度极低,充气过程中真空罐内气体温度接近风洞运行总温,为了简化计算,直接取温度T=T0;p02为风洞正常启动所需的出口限制压强,一般设为设计马赫数的波后总压(p01= 3 × 106Pa情况下约为88 953 Pa);p为风洞启动前真空罐内的初始压强,其值一般由真空泵的性能决定,目前市面上能直接采购到的真空泵一般可以将真空罐内的真空度抽到100 Pa以下。
在理想情况下,计算得到真空罐所需最小容积Vc≈ 3 m3。由于风洞实际运行过程中,往往在2~3个有效周期中截取一个有效周期,充气过程不可能完全符合简化的假设理论情况。因此为确保风洞平稳正常的运行,在得出真空罐最小理论许用容积后,乘于安全系数2,得到最后真空罐的设计容积为6 m3。
3 数值模拟计算与分析
风洞完整运行过程的非定常模拟使用二阶有限体积法的SU2开源求解器[17],湍流模型采用标准k-ωSST模型[18],空间离散采用AUSM格式[19]。
3.1 网格结构与边界条件设置
为了获得更为准确的结果,同时控制全风洞模拟的网格量,风洞建模采用1/2模型且均采用结构化网格,壁面第一层网格高度y+取5,网格在快开阀还有储气段弯管处进行加密,局部细节如图7所示。模型出口定义为压力出口边界,对称面采用对称边界,壁面则采用无滑移绝热壁面边界,储气段初始运行总温为430 K,总压为1 × 106Pa。

图7 风洞各部分网格拓扑结构Fig. 7 Mesh topologies for each part of the wind tunnel
由于Laval喷管内的流场变化较大,流动速度较快,重点对喷管部分开展网格独立性验证。喷管周向的网格分布参考Wu等之前已经开展过的研究[20],轴向和径向分别比较了648 × 72、724 × 81、809 × 90、905 × 101、1 131 × 126五种不同网格点分布下Laval喷管出口处的马赫数分布。由图8可知,网格点为905 × 101与1 131 × 126时的马赫数分布曲线几乎重合,故后续Laval喷管流场模拟选择使用905 × 101网格。

图8 网格无关性分析Fig. 8 Mesh independence test
3.2 风洞运行流场分析
3.2.1 Laval喷管流场启动
图9 显示了风洞启动过程喷管区域的流场变化云图,可以看出风洞启动后激波迅速沿着Laval喷管扫过,流动从喷管扩张段开始迅速加速通过喷管出口,并在8 ms以后实验段内的流场逐渐趋于稳定,表明高超声速流动启动完成。

图9 喷管启动过程马赫数云图Fig. 9 Mach number contours in the tunnel during the starting process
进一步提取Laval喷管内的流场数据进行定量分析,图10、图11分别显示了风洞启动过程喷管出口和中心轴位置的马赫数分布曲线,可以得知稳定后的实验段内的马赫数主要集中在马赫数6附近,喷管出口马赫数最大相对偏差约为3.1‰,优于国军标GJB 4399-2002[21]马赫数最大相对偏差要求。

图10 不同时刻喷管出口马赫数分布Fig. 10 Mach number distributions at nozzle outlet at different times

图11 不同时刻喷管中心轴马赫数分布Fig. 11 Mach number distributions at the nozzle centerline at different times
3.2.2 储气段内膨胀波演化
为研究弯曲储气段对风洞运行状态的影响,对风洞运行过程中储气段内流场的密度梯度进行分析。通过风洞运行过程中储气段截面的密度梯度云图(图12),可以直观地看出膨胀波系在储气段内的演变过程。阀门开启后,由于储气段内的高压和喷管内的低压形成的压力差,膨胀波在快开阀门处产生并以声速向储气段上游传播,并在波头下游拉出一系列强度、传播速度不等的平面膨胀波系;在26 ms通过弯管后,由于管壁的阻挡以及离心力的作用,膨胀波系会发生反射、变形并相互作用;t= 49 ms时膨胀波波头到达储气段端部并发生压缩和反射,波系再次相互作用并在反射后的波头下游拖出两条轴向长条状波系;之后膨胀波再次经过弯管并于t= 100 ms左右回到快开阀门位置。

图12 风洞运行过程储气段内的密度梯度云图Fig. 12 Density gradient in the storage section during the tunnel operation process
提取储气段轴线的密度梯度数据如图13所示,可通过d-t的斜率分析膨胀波行进的速度。在快开阀门刚开启时,基本只存在一段强度很强的汇聚膨胀波,随着膨胀波向储气段下游传播,其逐渐分成三个部分:范围连续、强度中等的波头(深灰色),范围集中、强度最大的波中(黑色点状),范围最广、强度最弱的波尾(浅灰色波纹状)。三个部分的膨胀波传播速度按照波头、波中、波尾依次递减,因此在风洞运行过程中膨胀波系的影响范围不断扩大。d-t的斜率在弯管位置基本没有变化,因此其对膨胀波系传播速度的影响可忽略不计。

图13 风洞运行过程储气段内膨胀波系x-t波图Fig. 13 x-t diagram of expansion waves in the storage section during the tunnel operation process at storage section
进一步对膨胀波系的强度变化进行分析。如图14所示,可以看出随着波系的传播,其扰动强度不断震荡并逐渐减弱,尤其是在经过弯管之后,其下降幅值相比经过储气段端部反射造成的变化要大得多,这可能是由于弯管离心力和壁面造成膨胀波系在管壁内不断变形、反射,同时相互作用造成的。
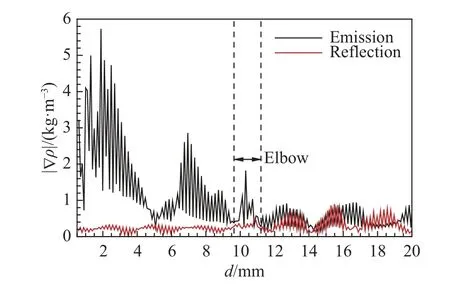
图14 风洞运行过程储气段内膨胀波系强度变化曲线Fig. 14 Intensities of expansion waves in the storage section during the tunnel operation process
4 Ludwieg管风洞来流校测
华中科技大学(HUST)Φ0.5 m马赫6 Ludwieg管风洞于2021年完成调试,如图15所示,为了满足常规高超声速气动力的研究需求,风洞运行时间为100 ms,有效运行总压范围为0.5~3 MPa,运行总温最高可达650 K,对于马赫数6流动而言,在防冷凝温度下最大可模拟单位雷诺数达到3.2 × 107/m,每天可运行50车次以上。该Φ0.5 m风洞流场总长约为20 m,最大宽度约为1.5 m,设备主体占地约为30 m2,其他负责系统占地空间可忽略。

图15 华中科技大学Φ 0.5 m马赫6 Ludwieg管风洞Fig. 15 HUST Φ 0.5 m Mach 6 Ludwieg tube wind tunnel
在静态马赫数分布测量实验中,风洞运行总压为1 MPa,总温为430 K,自由来流单位雷诺数为9.3 × 106/m(参考长度l= 1 m);在动态流场脉动测量实验中,风洞的自由来流单位雷诺数范围为4.31 × 106~1.08 × 107/m。
4.1 测量方法
4.1.1 实验状态参数
实验过程中总压测量采用的是MEAS-M3200系列压力变送器,该传感器量程选用0~4 MPa,供电电压为5 V,输出电压为0.5~4.5 V,响应时间小于2 ms,适用环境温度为-40~125℃。其可以承受50g的机械冲击和±20g的机械振动,非常适合用于测试风洞启动过程复杂的流动情况,且其动态响应速度足够捕捉风洞储气段中的流动。实验过程中的总温测量采用的是OMEGA的HKMQSS系列K型热电偶,其上限温度可达700 ℃,热电偶直径仅0.025 mm,且将热电偶结暴露在空气中以获取更快的响应频率,响应时间约为3 ms。总压、总温传感器均布置在风洞喷管入口附近以获取准确的流场状态参数。
4.1.2 自由来流流场参数
在风洞实验段中采用装有7个压力传感器的皮托耙对风洞来流马赫数的均匀度进行测量,图16为实验段中安装的皮托耙模型。模型传感器选取Honeywell的TruStability SSC系列压力传感器,传感器量程为0~15 psi,供电电压为5 V,适用温度为-20~85℃。皮托耙单个测试探头内径为3 mm,外径为4 mm,各个相邻探头间距离均为50 mm,整个皮托耙可测试直径350 mm区域内的流场数据。

图16 皮托耙Fig. 16 Pitot rake
动态测量采用的是装有PCB132B38高频压电式传感器的皮托探头(图17),该传感器工作温度-25~79℃,出厂校准灵敏度139.9 mV/psi,压力测量解析度1 mpsi,有效动态响应范围为11~1 000 kHz,可以测得在固定滞止压力条件下的压力脉动。

图17 皮托探头Fig. 17 Pitot probe
为检测皮托探头前激波强度和形态变化,进一步验证风洞启动和稳定所需的时间,采用纹影系统对试验段内的皮托探头进行拍摄。由于实验场地大小的限制,系统采用灵敏度较高的单反射式锥形光路设计(图18),采样设备为IDT-NX系列高速相机,采样频率为1 000 帧/s。

图18 纹影光路图Fig. 18 Schlieren optical path diagram
4.2 结果分析
4.2.1 静态流场品质
通过喷管入口附近安装的热电偶和压力传感器可获得风洞运行过程中的喷管入口总温T0和总压p0变化。由图19的总温曲线可以看出阀门开启后,储气段内高温高压气体向下游流动,入口温度有约14 K左右的上升后逐渐趋于稳定。
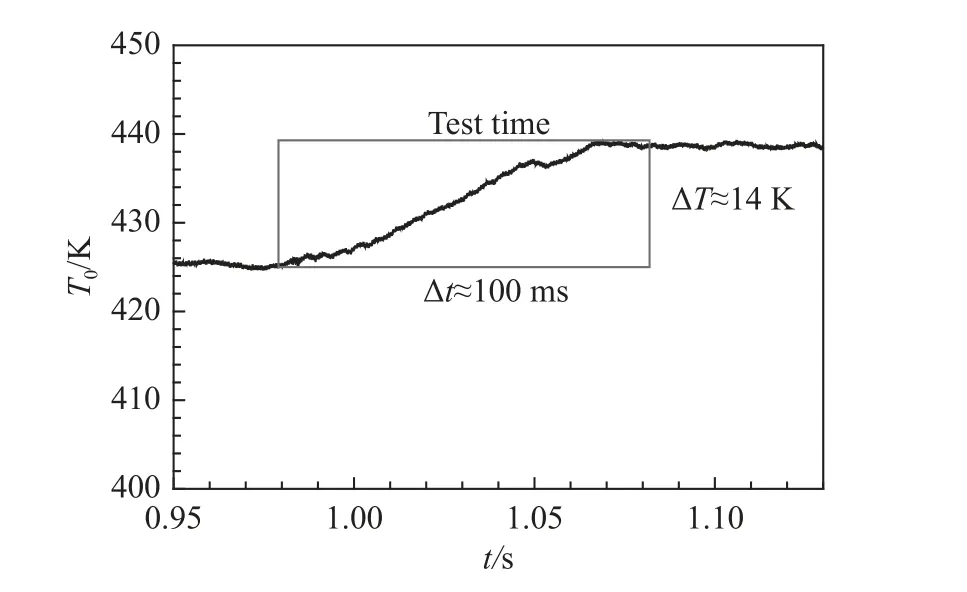
图19 喷管入口总温随时间变化曲线Fig. 19 Time histories of total temperature at nozzle inlet
图20黑色实线显示的是喷管入口的总压p0变化,可以看出风洞约5 ms完全启动(即快开阀门开启时间),风洞启动瞬间膨胀波以声速向上游扫过,导致总压阶梯下降,后保持稳定,当膨胀波接触到储气段尾端时反弹并传播回快开阀门位置,总压再次阶梯下降,阀门关闭风洞停止运行。该过程持续约100 ms,即为风洞有效运行时间,该结果与之前数值模拟结果吻合。

图20 喷管入口总压与皮托耙总压随时间变化曲线Fig. 20 Time histories of total pressure at nozzle inlet and pitot rake
将7孔皮托耙安装在风洞喷管的出口位置,通过测量皮托管激波后的总压,结合喷管入口的总压p0,经式(10)换算可获得风洞运行时实验段自由来流的马赫数分布。

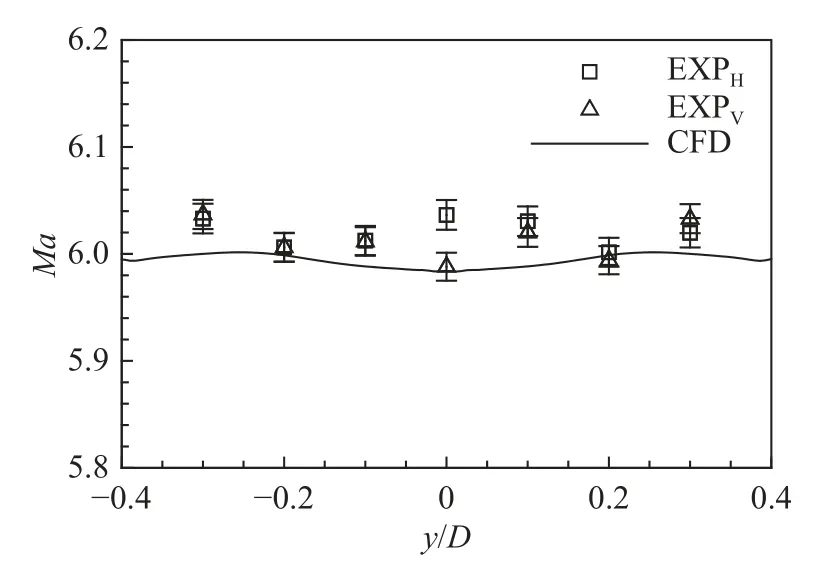
图21 喷管出口处马赫数横向、纵向分布比较Fig. 21 Comparison of horizontal and longitudinal Mach number distributions at nozzle outlet
将皮托探头的纹影图像与相同流动条件下的CFD模拟结果进行了对比如图22所示。所得弓形激波的形状基本与数值模拟结果一致,进一步验证了风洞实验段的马赫数6高超声速来流。

图22 Pitot探头纹影实验与数值比较Fig. 22 Comparison between Pitot probe measurements and numerical results
4.2.2 动态流场品质
通过采用安装有PCB高频压力传感器皮托探头获取风洞自由来流的压力扰动RMS值,以此检测风洞的动态流场品质,并与风洞参数相似的德国不伦瑞克大学HLB风洞、美国空军学院HHK-6Φ0.5 m Ludwieg管风洞进行了比较[8]。
图23显示了上述风洞在同一位置(风洞轴线处)的RMS数据比较。数据均使用了相同的测量设备及处理方式,信号滤波范围5~1 000 kHz,结果用探头的波后总压来归一化。所有数据显示,在Re/l= 4 × 106~12 × 106/m范围时,来流压力扰动强度均随Re的增大呈下降趋势,归一化压力脉动从1.5%降至0.7%水平。总体而言,HUST风洞的流场品质在不同单位来流雷诺数下均优于HHK-6和HLB风洞。

图23 不同风洞来流的压力扰动幅值Fig. 23 Amplitude of freestream pressure disturbances in different wind tunnels
对测压后的数据进行PSD功率谱密度分析。使用Welch方法,选取Blackman窗函数,窗大小为1 × 210样本点,选取overlap为50%,其结果如图24所示。由此可见,本风洞中自由来流的扰动能量幅值均低于HHK-6与HLB风洞,进一步体现了本风洞来流流场品质相对较好,适合开展高超声速风洞实验基础研究。
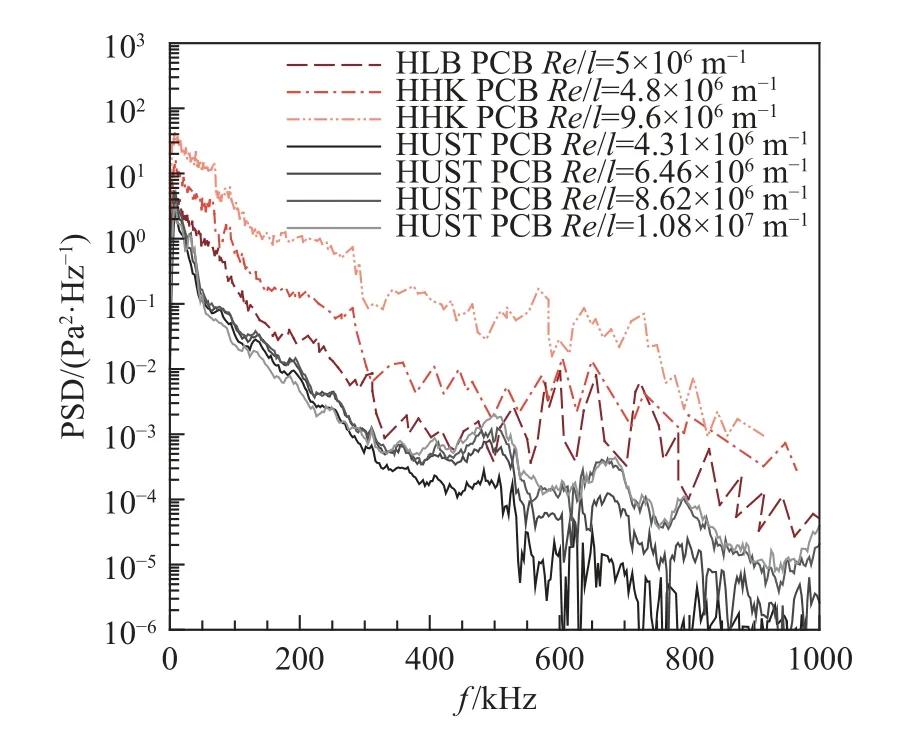
图24 不同风洞来流的压力扰动PSD图Fig. 24 Freestream PSD of pressure disturbances in different wind tunnels
5 结 论
本文介绍了华中科技大学Φ0.5 m口径马赫6高超声速Ludwieg管风洞气动设计,分别从数值和实验两个方面评估了该Ludwieg管风洞的流场品质,通过研究可得出以下结论:
1)采用快开阀主控Ludwieg管高超声速风洞的启停方案可行,使用快开阀的喷管可在10 ms内建立起稳定的高超声速流动,且对Laval喷管核心流动区域马赫数分布的均匀性分布影响不大,该设计可以大幅提高高超声速Ludwieg管的运行效率,并有效降低其建设与运行成本;
2)弯管设计对风洞运行过程中储气段内膨胀波的传播有一定影响,膨胀波系的传播速度经过弯管基本不变,但强度会明显减弱,这可能是由于膨胀波系在弯管内不断反射并相互作用造成的;
3)本风洞在总温430 K状态下运行的有效时间为100 ms,且自由来流的状态在运行过程中保持恒定,风洞实验段的马赫数均方根偏差为1.55%,达到国军标(GJB1179-91)马赫数均方根偏差要求;皮托管压力扰动幅值在单位来流雷诺数4.31 × 106~1.08 ×107/m范围内为1.5%~0.7%,与HHK-6和HLB相比低40%~70%左右,展现了该实验平台更优的动态流场品质。
4)本风洞的运行费用主要来自动力源,包括空气压缩机(约15 kW)、储气段加热器(约45 kW)及真空泵(约7.5 kW),风洞运行车次间隔通常为10 min,单车次运行总功耗约11 kW·h,成本低廉,适合高等院校作为基础研究平台使用。
通过以上研究表明,采用弯折长直储气段设计的快开阀主控型Ludwieg管设计可行,该高超声速风洞具有流场品质高、重复性好、可模拟单位雷诺数高、建设和运行成本低、操作简单等优点,适合开展高超声速模型的气动力精细化地面实验研究,满足诸如高超声速湍流多尺度问题、高超声速飞行器内外流耦合以及高超声速边界层转捩等关键技术问题的研究需求。
