格尼襟翼对旋转导弹气动特性的影响

2023-02-22寇少博冯立好刘松彬徐华松

空气动力学学报 2023年1期

寇少博，冯立好，*，李晓，杨欣，刘松彬，徐华松

(1. 北京航空航天大学流体力学研究所，北京 100191；2. 上海机电工程研究所，上海 201109)

0 引言

旋转导弹是指飞行过程中绕其纵轴自旋的一类导弹，为简化控制系统，其气动布局一般采用鸭式布局[1]。旋转导弹以其轻便高效、制导精度高、成本低、易于扩展应用等诸多优势，已成为导弹武器的重要分支，在近程和末端防御领域有不可替代的地位[2]。

旋转导弹的自旋运动使其在飞行过程中具备一定的轴向稳定性，但自旋运动也带来更加复杂的气动问题，如马格努斯效应等。马格努斯效应会使弹体产生额外的侧向力及力矩[3]，进一步加剧弹体的非定常气动特性，而鸭式布局旋转导弹的鸭翼尾涡会对弹体的气动特性产生进一步影响[4]。

关于旋转导弹的研究涉及制导控制、结构及气动布局等多学科领域，近年来关于旋转导弹的研究以制导控制等领域居多[5-7]，气动特性及流动控制等方面的研究较少。实验中主要通过非定常气动力的变化分析旋转导弹的复杂气动问题。除实验手段外[8-12]，研究人员还通过数值模拟开展了一系列旋转导弹气动特性的研究[4,13-18]。

Burkhalter和Heiser[13]提出了FM-3旋转导弹标模，该模型通过斜置尾翼的方式来产生使导弹旋转的滚转力矩。Nygaard和Meakin[14]基于FM-3标模研究了黏性效应对计算结果的影响及导弹滚转角速度对其气动特性的影响规律。结果表明，黏性效应主要表现在鸭翼涡系与导弹边界层的相互作用中，当鸭翼偏转角较小时，即鸭翼涡系强度较低时，黏性效应较弱，无黏结果与黏性结果相近；导弹滚转角速度的变化对导弹平均气动力及气动力矩的影响较小，且除滚转力矩外，导弹静态计算结果与动态计算的瞬时解相差较小。为进一步提高数值模拟方法的计算效率，陈白冰等[18]将旋转壁面法应用于旋转导弹的数值模拟研究，通过给弹体附加旋转速度模拟真实的弹体旋转运动，可采用定常求解方式，从而简化了计算方法，提高了马格努斯力矩的计算效率。

目前旋转导弹通常采用斜置尾翼产生维持导弹旋转的滚转力矩，以适应单通道控制体制。实际加工、组装过程中，斜置尾翼安装角度存在一定误差，影响了转速稳定性，并且存在转速不足、易失稳、难以主动控制等问题[9,19-20]。因此，探究不同的旋转导弹设计方式，对于进一步提高旋转导弹的气动性能、改善其转速稳定性具有重要意义。

格尼襟翼是一块垂直放置于翼型下翼面后缘附近的扰流片，通过增加翼型的有效弯度以改善翼型的气动特性。格尼襟翼因其结构简单、增升效果明显而备受关注[21]。研究人员将格尼襟翼应用于低速翼型[22]、超临界翼型[23]、三角翼[24]、双三角翼[25]及风力机叶片等[26]，均取得良好的增升效果。将格尼襟翼应用于导弹尾翼施加控制，则可利用其增升特性产生滚转力矩，进而代替斜置尾翼。

2016年，刘郑州等[20]基于拉姆导弹的尾翼设计，研究了尾翼加装格尼襟翼对旋转导弹气动特性的影响。结果表明，格尼襟翼主要提高了导弹在亚跨声速阶段的滚转力矩，从而提高了弹体在被动段的转速，使得提高导弹被动段制导精度成为可能。他们主要通过尾翼后缘偏折的方式达到格尼襟翼控制效果，且侧重于研究来流马赫数及格尼襟翼几何参数对导弹气动特性的影响。一方面，在Li等[27]的研究中，格尼襟翼的安装角度在接近90°时增升效果最好，且垂直于尾翼弦线安装格尼襟翼的加工工艺更加简便，对导弹结构影响小，易于扩展；另一方面，关于格尼襟翼对旋转导弹气动特性影响的流动机理尚缺乏足够认识。

因此，本文在导弹尾翼后缘处安装垂直于尾翼弦线的格尼襟翼，以研究格尼襟翼在不同来流马赫数、导弹迎角时对导弹气动特性的影响规律，并通过分析导弹流场特性揭示控制机理。

1 控制方案与研究方法

1.1 控制方案设计

导弹的外形设计参考Burkhalter和Heiser[13]提出的FM-3标模，导弹外形为典型的鸭式布局，其尾翼存在1°斜置角度以产生导弹旋转所需的滚转力矩。该导弹模型旨在为旋转导弹的数值模拟研究提供通用模型，Nygaard和Meakin[14]、Murman等[15]、Blades和Marcum[16]利用数值模拟方法对FM-3标模开展了相关研究。

本文对FM-3标模的尾翼进行进一步处理，以支撑控制方案设计。将原有的斜置尾翼改为平置尾翼，并在尾翼后缘靠近翼尖的一侧布置格尼襟翼，格尼襟翼垂直于尾翼弦线，展向长度是尾翼展长的50%，如图1所示。从导弹尾部看，格尼襟翼沿逆时针方向布置，以产生顺时针方向的滚转力矩。

图1 导弹控制方案设计Fig. 1 Control scheme design of the missile

为更好地对比分析，本文共设置5种导弹模型，分别为无格尼襟翼布置、平置尾翼的基本模型（Baseline），无格尼襟翼布置、1°尾翼斜置角的模型（1° Oblique tail），平置尾翼、尾翼后缘分别布置高度为1%、2%、4%尾翼平均几何弦长的格尼襟翼的模型（1%c、2%c、4%cGurney flap）。

1.2 计算方法与可靠性验证

流体运动方程为三维Navier-Stokes（N-S）方程，采用有限体积法进行空间离散，采用压力基求解器，时间上为稳态求解，对流项与黏性项均采用二阶精度格式。湍流模型为SSTk-ω模型，流场介质为空气，密度计算采用理想气体条件，黏性系数计算采用Sutherland公式，边界入口条件为压力远场条件，导弹壁面为无滑移壁面条件。

计算所采用的网格类型为混合网格，导弹壁面附近采用结构网格，其余区域为非结构网格，计算域为圆柱型，圆柱高为特征长度14倍，半径为特征长度3倍，其中特征长度为弹身几何长度。为验证计算网格质量与无关性，绘制三套不同密度的网格，网格数量分别为100万（Coarse mesh）、200万（Medium mesh）、300万（Fine mesh），并计算导弹在来流马赫数Ma= 0.6时不同迎角下的法向力系数。计算结果如图2所示，随着网格数量增加，导弹的法向力系数趋于稳定值，其中，200万网格与300万网格所得计算结果几乎相同。因此，为提高计算效率，本文选取网格数量200万的网格进行后续数值模拟研究。

图2 网格无关性验证Fig. 2 Grid independence validation

本文采用准静态拟合动态实验数据的方法[14]进行数值计算结果的验证。采用1°尾翼斜置角模型与Burkhalter和Heiser[13]的实验结果进行对比。由于本文所采用模型的鸭翼与弹身固连，且鸭翼偏转角为0°，因此，选择Burkhalter和Heiser[13]实验结果中包含导弹滚转角与鸭翼偏转角变化曲线的实验工况，并选取该工况中导弹鸭翼偏转角为0°时所对应的4个导弹滚转角，在来流马赫数Ma= 1.6、导弹迎角α=0°时，将模型设置同样的滚转角进行计算。本文获得的导弹模型法向力系数与文献中的实验结果基本一致，如图3所示，验证了本文计算结果的可靠性。此外，Burkhalter和Heiser[13]的实验结果中，不同迎角下导弹法向力系数随滚转角变化曲线的整体趋势一致，差异较小，仅平衡位置有所差别。因此，本文对单个迎角所做的计算精度验证，可以涵盖更高迎角的计算结果，能够作为5种模型气动特性分析的依据。

图3 法向力系数计算结果与实验结果对比Fig. 3 Computed normal force coefficient compared to the experimental result

2 气动特性分析

本节分别计算了5种模型在导弹滚转角Φ=0°时在亚声速（Ma= 0.6）和超声速（Ma= 1.6）不同迎角的气动力及气动力矩系数，研究在不同迎角及来流马赫数下，格尼襟翼对导弹滚转力矩、法向力及侧向力等的影响规律，分析导弹附近流场旋涡演化及压力分布特性，揭示格尼襟翼产生滚转力矩、影响导弹气动特性的流动机理。其中，模型气动力及气动力矩计算均基于弹体坐标系，坐标系原点位于弹体头部，模型迎角变化基于风轴坐标系。

2.1 亚声速气动特性

由图4（a）可知，在亚声速来流时，5种模型的法向力系数差异较小，其中α= 20°时，4%c格尼襟翼模型与基本模型的法向力系数相差6%。

对于影响导弹操纵性的侧向力而言，如图4（b）所示，在亚声速来流时，各模型随着迎角增大，其侧向力系数都有不同程度的增长。在小迎角（α≤ 8°）时，5种模型的侧向力系数变化较小，相差不大；随着迎角进一步增加（α＞ 8°），非线性流动增强，5种模型的侧向力系数都有不同程度的增长，除基本模型外，其余4种模型均在α= 30°左右达到极值。格尼襟翼模型侧向力系数随迎角增加近似呈线性变化，而斜置尾翼模型的侧向力系数则在迎角α＞ 20°时迅速增长，且其极值点α= 32°的侧向力系数值与1%c格尼襟翼模型相比增加了98%。

对于导弹的滚转力矩系数而言，如图4（c）所示，除基本模型外，其余4种模型的滚转力矩系数绝对值均随迎角增大而减小，如4%c格尼襟翼，在α= 36°时的滚转力矩系数仅为α= 0°时的52%。由图4（c）可知，当格尼襟翼高度增加，格尼襟翼模型的滚转力矩系数也随之增加，且均大于斜置尾翼模型的滚转力矩系数，其中，α= 0°时，与斜置尾翼模型相比，1%c、2%c、4%c格尼襟翼的滚转力矩系数分别增加了178%、272%、392%。

图4 Ma = 0.6时气动载荷随迎角变化Fig. 4 Variation of the aerodynamic load with the angle of attack at Ma = 0.6

进一步，在导弹巡航状态下，较小的侧向力系数能够保证导弹巡航飞行的稳定性。巡航飞行一般为小迎角飞行。以α= 4°为例，此时，与斜置尾翼模型相比，1%c、2%c、4%c格尼襟翼的滚转力矩系数分别增加了156%、241%、352%，而侧向力系数相差较小。由此可知，当α= 4°，相比于斜置尾翼模型，格尼襟翼模型在提供更大滚转力矩的同时，并未对导弹侧向力产生明显影响。且当迎角进一步增大时，相比于斜置尾翼模型，格尼襟翼模型的侧向力系数增长缓慢，且呈线性发展，进一步降低了对导弹操纵性的影响，更有利于导弹的巡航飞行。

导弹在发射、机动飞行等阶段属于大迎角飞行状态，因此对于导弹大迎角气动特性的研究具有重要意义。以α= 36°为例，此时，与斜置尾翼模型相比，1%c、2%c、4%c格尼襟翼的滚转力矩系数分别增加了8倍、10倍、13倍之多，而侧向力系数仅为斜置尾翼模型的56%、40%、32%。由此可知，当α= 36°，相比于斜置尾翼模型，格尼襟翼模型在提供更大滚转力矩的同时，也使得导弹侧向力进一步减小，对导弹操控性影响更小。

此外，图4中基本模型的侧向力系数与滚转力矩系数均不为0，主要是由于导弹大迎角下流动分离等强非线性效应所导致的。该现象在导弹大迎角飞行时普遍存在[28-30]，不完全是计算误差的影响，且本文关注的重点是格尼襟翼对导弹气动特性的影响规律，5种模型所采用的数值模拟方法完全一致，格尼襟翼模型气动特性分析的过程及结论主要基于与基本模型及斜置尾翼模型的对比分析，在保证数值模拟方法一致的前提下，计算误差不会影响本文的主要结论。

为了解亚声速时滚转力矩系数变化的流动机理，分析基本模型及4%c格尼襟翼模型S1截面的压力云图（图5）。由图5可知，基本模型的两尾翼压力沿弹身轴线对称分布，外侧区域为低压区，中间区域前缘附近为高压区，后缘附近为低压区，在尾翼尾流区存在局部高压区。在尾翼后缘放置格尼襟翼后，其影响区域主要为尾翼后缘附近流场。若定义格尼襟翼所在翼面为下翼面，α= 4°时，两尾翼后缘附近的下翼面均出现高压区，上翼面负压增强，与基本工况相比压力分布呈现显著非对称特性，从而产生了使导弹沿x轴旋转的滚转力矩；α= 16°时，格尼襟翼控制工况的压力分布形态虽然与未控制工况相似，但是正压和负压强度增加，分布范围增大，并且呈现不对称特性，进而提供滚转力矩。

图5 导弹S1截面压力系数分布Fig. 5 Pressure coefficient distribution in section S1 of the missile

为揭示格尼襟翼模型与斜置尾翼模型气动特性差异的流动机理，研究了5种模型旋涡演化和S2截面压力分布特征，如图6所示。格尼襟翼使得各尾翼后缘附近产生了非对称涡结构，并且随着格尼襟翼高度增加，旋涡强度增大，尾翼上下两侧的吸力和压力分别增加；与之相比，基本工况和斜置尾翼模型的旋涡分布较为对称，上下翼面呈现较为对称的压力分布特性。因此，在现有工况下，亚声速时格尼襟翼模型的滚转力矩系数均大于斜置尾翼模型。

此外，由图6中的涡系云图可知，格尼襟翼仅增强了尾翼附近流场旋涡结构强度及分布，并未明显改变导弹弹体附近流场及旋涡分布，包括鸭翼所产生的旋涡结构。因此，在尾翼后缘安装格尼襟翼对导弹的法向力影响较小。上述结果进一步表明，格尼襟翼在不改变法向力的前提下能够提供较大的滚转力矩，具有显著的控制优势。

图6 Ma = 0.6，α = 4°时五种不同模型Q准则识别的三维旋涡结构(a～e)及S2截面压力系数分布(f～j)Fig. 6 Three-dimensional vortices identified by Q criteria (a～e) and pressure coefficient contours in section S2 (f～j) for five different models at Ma = 0.6, α = 4°

2.2 超声速气动特性

如图7（a）所示，在超声速来流时，5种模型的法向力系数的差异较小，其中α= 8°时，4%c格尼襟翼模型与基本模型的法向力系数相差仅为1%。

超声速来流时，导弹侧向力系数的变化如图7（b）所示。随着迎角增大，基本模型的侧向力系数在0附近波动，1%c与2%c格尼襟翼模型的侧向力系数随迎角增大出现极大值，4%c格尼襟翼模型与斜置尾翼模型的侧向力系数随迎角增大而增大。与亚声速来流相比，超声速来流下，格尼襟翼使模型的侧向力系数出现不稳定增长，但是依然比斜置尾翼模型的侧向力系数数值更小。

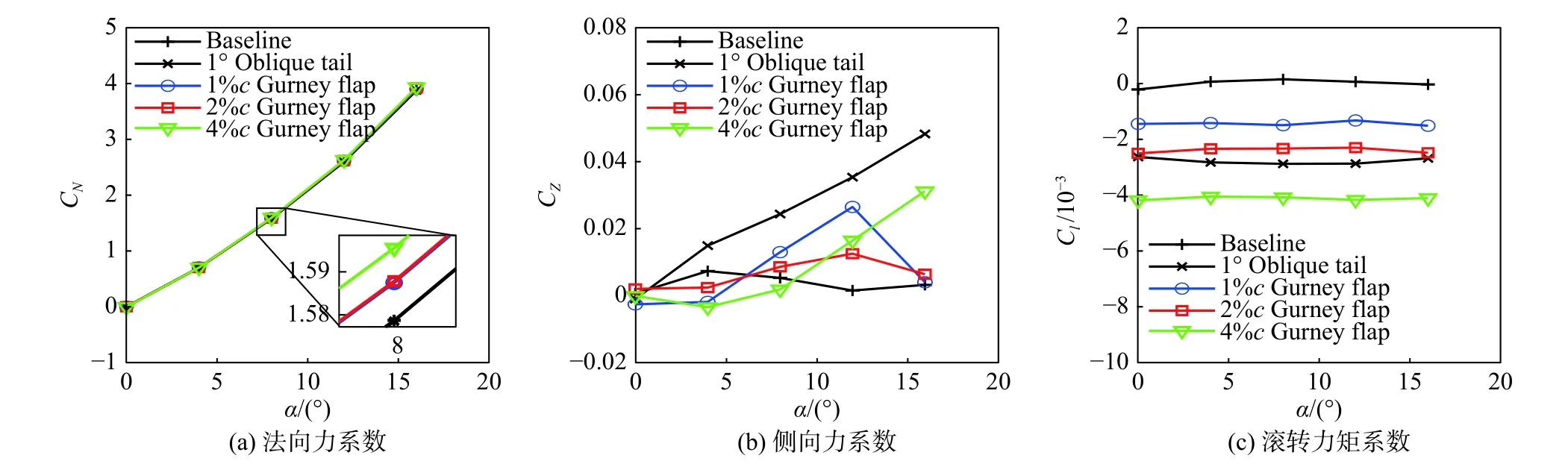
图7 Ma = 1.6时气动载荷随迎角变化Fig. 7 Variation of the aerodynamic load with the angle of attack at Ma = 1.6

由图7（c）可知，超声速来流时，随着迎角增大，5种模型的滚转力矩系数均变化较小，如4%c格尼襟翼，在α= 16°时的滚转力矩系数与α= 0°时仅相差2%；在同一迎角下，格尼襟翼模型的滚转力矩系数随格尼襟翼高度增加而增加，此时2%c格尼襟翼模型的滚转力矩系数与斜置尾翼模型相近。结合图7（b）可知，相较于斜置尾翼，4%c格尼襟翼在产生更大滚转力矩系数的基础上，对于侧向力的影响更小。如α= 4°时，4%c格尼襟翼的滚转力矩系数相比斜置尾翼模型增加了53%，但侧向力系数仅为斜置尾翼模型的65%。对比不同来流马赫数下的滚转力矩系数可知，与亚声速来流相比，超声速来流时格尼襟翼的操纵效率变低，如α= 0°时，4%c格尼襟翼在Ma=1.6时的滚转力矩系数仅为Ma= 0.6时的36%。

为了进一步分析滚转力矩系数变化的流动机理，分别绘制基本模型及4%c格尼襟翼模型的S1截面及S2截面压力云图，分别如图8、图9所示。由图8可知，在超声速来流时，基本模型的各尾翼流动沿x轴近似呈对称分布，而由于激波的影响，尾翼上下翼面的流动不会相互干扰。因此，在尾翼后缘放置格尼襟翼后，处于尾翼下翼面的格尼襟翼主要改变下翼面流动结构，对上翼面流动影响较小。与基本模型相比，格尼襟翼使得尾翼后缘附近的下翼面压力增大，尾翼后缘附近的流场的非对称性较亚声速时明显减弱，因此，与亚声速来流相比，超声速来流下的格尼襟翼操纵效率明显降低，从而使得超声速来流时格尼襟翼产生滚转力矩系数明显减小。

图8 Ma = 1.6时导弹S1截面压力系数分布Fig. 8 Pressure coefficient distribution in section S1 of the missile at Ma = 1.6

由图9可知，在超声速来流下，格尼襟翼导弹模型的尾翼上翼面压力分布与基本模型相似，但是尾翼下翼面流场呈现很大的变化，且尾翼的高压区分布由于激波影响也存在一定差异。进一步表明超声速来流下，格尼襟翼依然通过产生翼面上下两侧压力的不对称性分布提供滚转力矩，但是由于激波影响，格尼襟翼的操纵效率相比亚声速来流时明显下降。

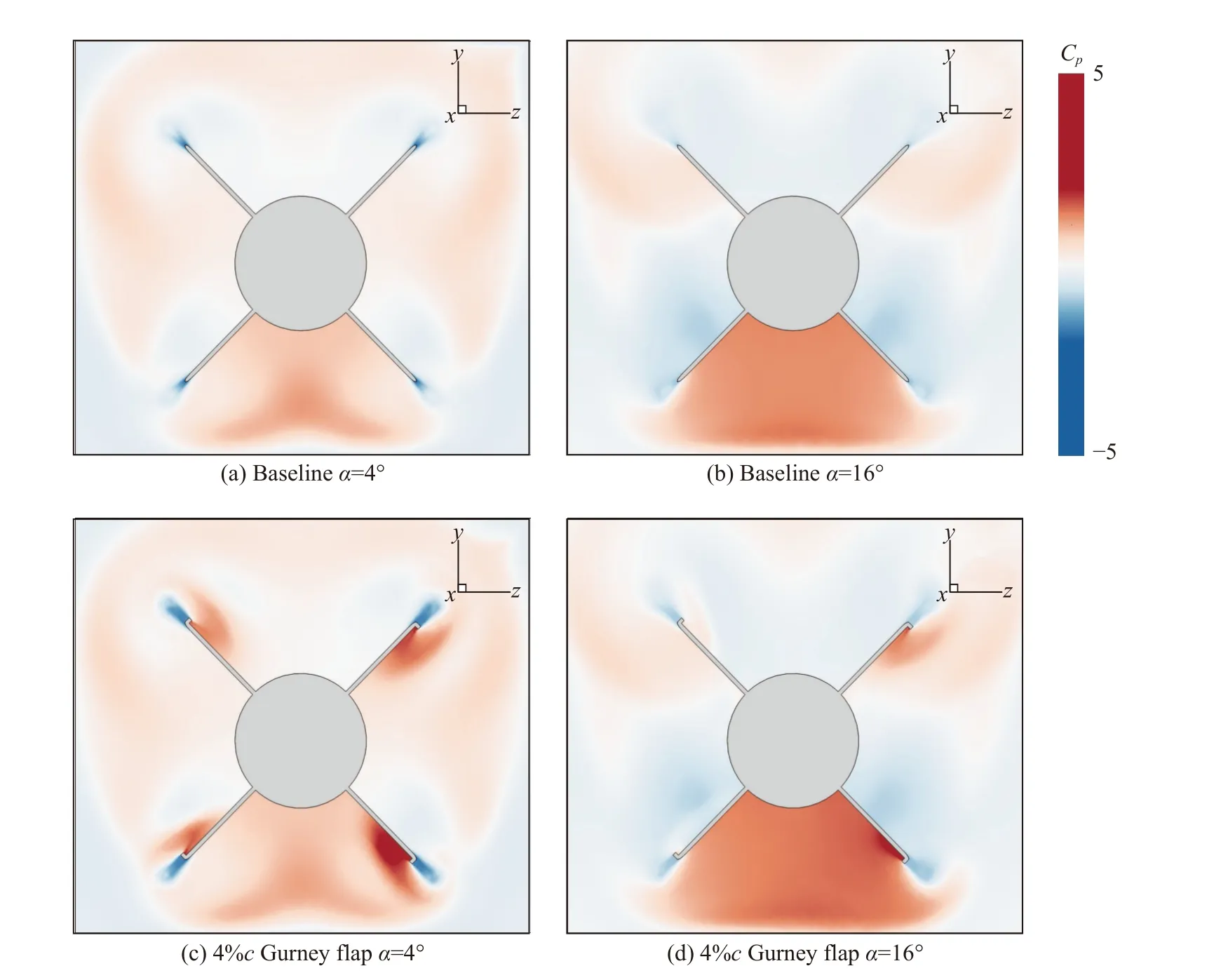
图9 Ma = 1.6时导弹S2截面压力系数分布Fig. 9 Pressure coefficient distribution in section S2 of the missile at Ma = 1.6

此外，当导弹迎角变化时，由图8（c、d）可知，在超声速来流下，当迎角增大至α= 16°时，与α= 4°时相比，下尾翼的下翼面高压区压力降低，但上尾翼非对称流动区域的正压与负压强度增加；由图9（c、d）可知，迎角增大后，非对称流动区域的分布范围呈现一定变化。但是，由图7（c）可知，不同迎角下导弹的滚转力矩相差较小。因此，在超声速来流下，格尼襟翼的操纵效率主要受到压缩性影响，导弹迎角变化对格尼襟翼的操纵效率影响较小。