基于两阶段模型的风光互补系统储能容量配置优化方法

李 伟，刘 立，王豪琦，何思敏

(三峡大学电气与新能源学院，湖北 宜昌 443000)

目前，随着全球生态环境的改变，新能源发电早已成为各个国家关注的热点问题，在新能源发电领域光伏与风电因其对环境破坏小，经济性好而得到了广泛应用。相比于单纯的光伏与风力发电，风光互补系统具有较好的相互补偿特性，但即使这样孤立风光互补系统依旧受自然条件限制很大，这就造成了风光互补系统发电的不确定性与较强随机性，而储能单元可以作为风光互补系统的补充电源，在弃风弃光时将电能以化学能的形式进行存储，而当负荷高峰期时，储能单元可以将化学能转换成电能，减少负荷缺电率，提升系统的稳定性。所以如何规划风光互补系统中储能容量的大小是目前研究的热点问题之一。

针对风光互补系统储能容量的规划问题，早已有很多学者进行了研究。文献[1]提出以新能源渗透率、消纳率、负荷匹配度作为风光互补性能评价指标，并使用分支界定法与Charnes-Cooper方法求解容量配置模型。文献[2]以风光互补系统跟踪调度曲线能力为指标，并采用一种变步长循环离散方法求解优化模型得到最优储能优化配置。文献[3]以综合成本最小为优化目标，运用遗传算法求解容量配置优化模型。文献[4]考虑风光出力的不确定性，建立风光出力模型，以系统新能源损失最小为目标函数求解储能容量配置。文献[5]应用机会约束规划理论建立了经济调度模型,并提出一种基于随机模拟技术的粒子群优化算法对系统的运行方案进行优化。文献[6-7]通过对风、光、储系统的建模，并对其进行经济性分析，得到了储能容量的最优配置。

以上所述文献中或就其技术性指标或就其经济性指标进行储能系统的规划，未能做到两者统一，而在实际工程中储能系统的建设需两者兼顾。本文提出基于两阶段模型的风光互补系统容量配置，系统包含光伏模块、风机、储能电池等。其中以负荷缺电率、新能源弃用率作为第一阶段的优化目标，在保证系统供电可靠性的同时确定储能容量优化区间。第二阶段以年新能源弃用成本与储能初始投资年均成本为目标函数确定储能的最优容量。并选取某地实际风光出力数据进行验证，证明了所提模型的有效性。

1 风光互补系统典型结构

风光互补系统的典型结构如图1所示，主要由4部分构成：风电单元、光伏组件、电池储能系统和本地负荷。风电、光伏发电单元和储能单元通过各自的DC/DC变换器汇总至直流公共母线，再经公用的DC/AC逆变器给负荷供电。

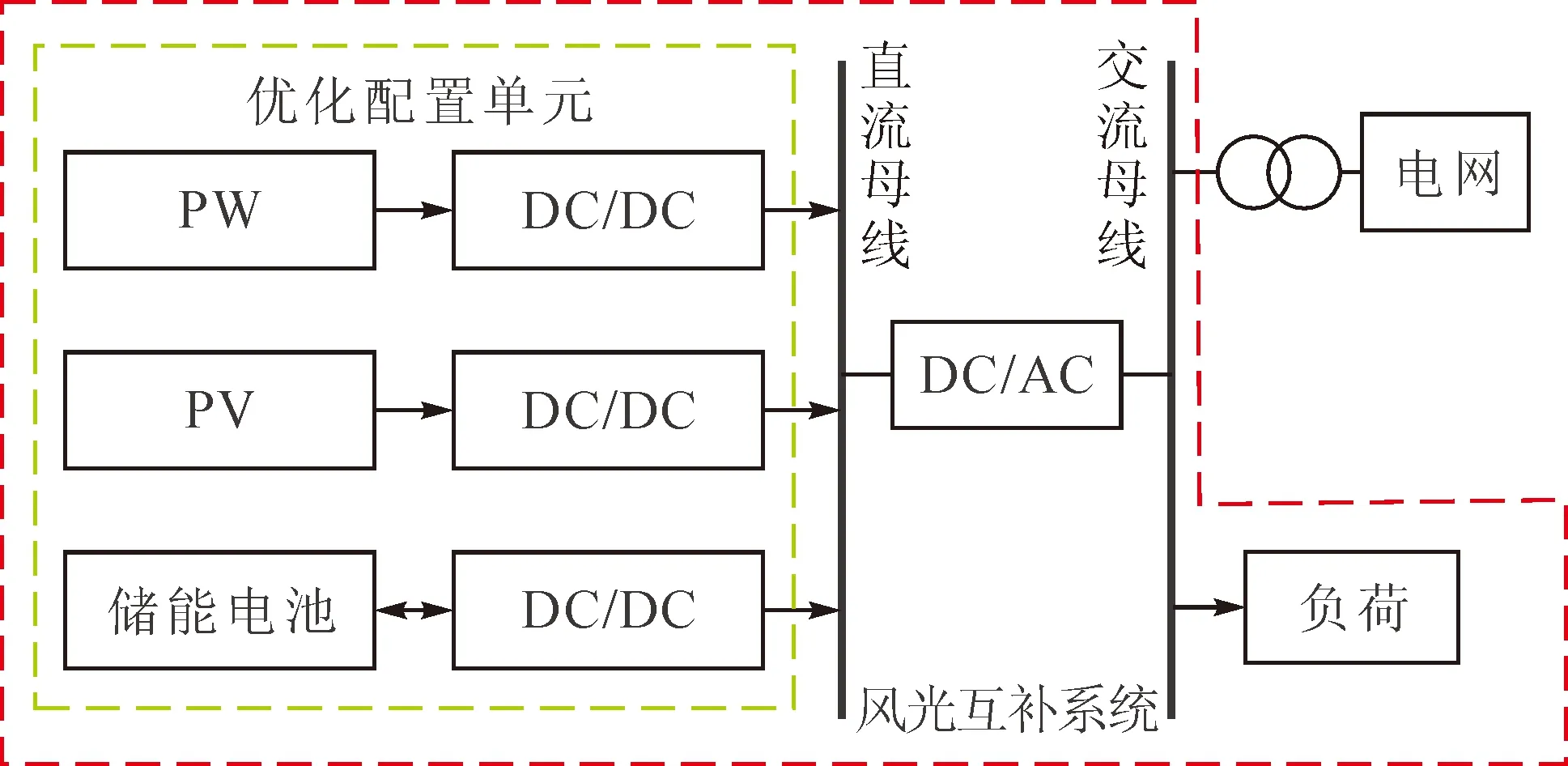
图1 风光互补系统典型结构图

2 系统技术指标

2.1 负荷缺电率

负荷缺电率表示一定时间内系统发电功率不能满足负荷需求的概率。在评价周期T内负荷缺电率可表示为该时段内的负荷缺电量与负荷总需求的比率。风光互补系统负荷缺电率表示方法：

QQD(t)=[PFH(t)-PPV(t)η1-PPW(t)η2]Δt

(1)

式中：PFH(t)为t时刻系统负荷需求；PPV(t)η1为t时刻光伏组件发出的平均功率；PPW(t)η2为风电发出的平均功率；η1为逆变器C1效率；η2为逆变器C2的效率。

负荷缺电量QQD(t)一般为正值，定义负荷缺电率QQDL为

(2)

式中：t0为初始时刻；n为时间序列；QQDL的取值范围为[0-1]，取0时表面在所求时间序列范围内风光互补系统所发出的功率满足负荷需求，取1时表明在所求时间段内风光互补系统所发出的功率不能满足负荷需求。

2.2 新能源弃用率

新能源弃用率指在时间T内系统弃用的新能源能量与可再生能源发出总能量的比值，常用作衡量可再生能源消纳水平，工程一般取5%～30%之间。风光互补系统新能源弃用率表示方法：

QQY(t)=[PPV(t)η1+PPW(t)η2-PFH(t)]Δt

(3)

新能源弃用量一般为正值，定义新能源弃用率QQYL为

(4)

3 容量配置优化方法

3.1 建立储能功率需求

在考核周期T内，设某一时刻t时系统的功率不平衡量为ΔP，则

ΔP(t)=PFH(t)-PPV(t)η1-PPW(t)η2

(5)

式中，ΔP(t)的正负值具有随机性，当ΔP(t)>0时表示储能需要放电，ΔP(t)<0时表示储能需要充电。

在进行功率配置时，需要储能单元能够满足或者吸纳所求时间段内出现的最大功率缺额P1，或者最大剩余功率P2，所以储能的定额功率PED为

(6)

式中，η3为储能变换器的效率。

3.2 建立储能容量需求

当风光互补系统的发电功率小于负荷时，储能系统向电网释放的容量ΔE为

ΔE=Δt[PFH(t)-PPV(t)η1-PPW(t)η2]/η4

(7)

式中，η4为储能系统放电效率。

当风光互补系统的发电功率大于负荷时，储能系统从电网吸收的容量ΔE为

ΔE=Δt[PPV(t)η1+PPW(t)η2-PFH(t)]/η5

(8)

式中，η5为储能系统充电效率。

4 容量配置优化方法

本文第一阶段模型考虑风光出力特性、储能出力特性等为约束，建立负荷缺电率、新能源弃用率指标。求解储能容量配置优化区间。第二阶段模型综合考虑新能源弃用年惩罚成本，储能初始投资年均成本。以新能源弃用年惩罚成本和储能初始投资年均成本最小为优化目标求解储能最优容量配置。求解流程如图2所示，具体求解步骤如下：

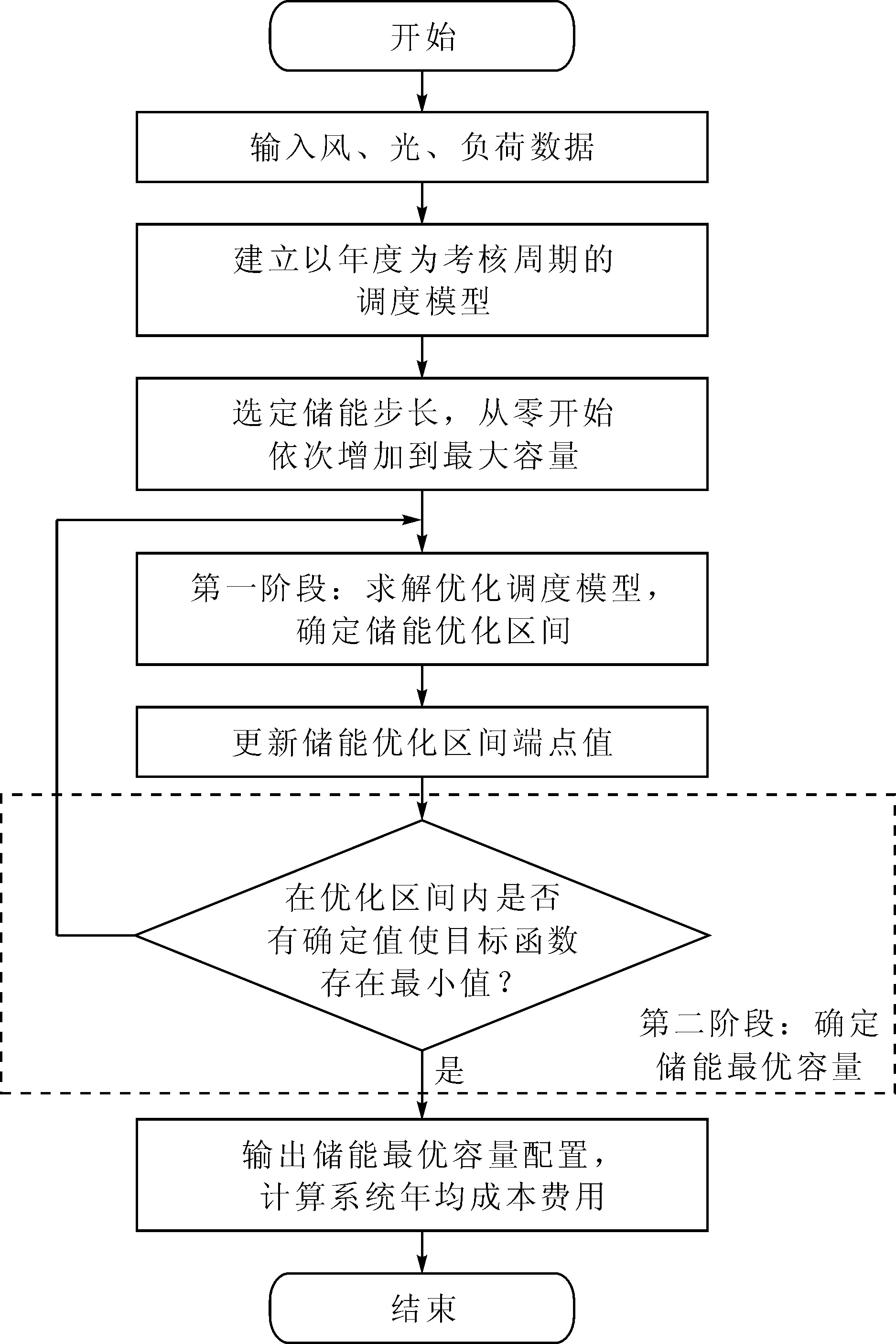
图2 求解流程图

1)输入风、光、负荷数据等；

2)储能容量从0开始，选定储能步长逐步增加到最大值，确定储能相关参数，具体包括功率、逆变器功率等；

3)设定负荷缺电率和新能源弃用率区间，建立以年度为考核周期的优化调度模型；

4)第一阶段，求解步骤2中建立的调度模型，在给定负荷缺电率和新能源弃用率区间前提下求解储能容量优化区间；

5)第二阶段，更新储能容量优化区间；

6)判断在当前储能容量优化区间内是否存在确定值使目标函数存在最优解，否则修改负荷缺电率和新能源弃用率区间执行步骤4，是则执行步骤7；

7)输出储能最优配置容量，计算系统总成本费用，流程结束。

4.1 目标函数

本文目标函数为新能源弃用年惩罚成本与储能初始投资年均成本最小。

minCXT=CEERATEφ+Fqy

(9)

式中：CXT为新能源弃用年惩罚与储能初始投资年均成本；ERATE为储能容量；CE为储能容量单位投资成本；Fqy为新能源弃用惩罚成本；φ为年均成本投资因子。

4.2 约束条件

1)风光出力约束

(10)

(11)

式中：Sw表示风电的实际装机容量；Sv表示光伏的实际装机容量。

2)负荷平衡约束

(12)

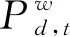
3)弃风弃光约束

(13)

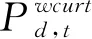
4)电储能约束

0≤SOCd,t≤Emax

(14)

(15)

(16)

(17)

(18)

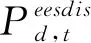
5)新能源弃用成本

(19)

6)储能单元现值因子

(20)

式中：r表示为储能单元贴现率；n表示储能单元的寿命。

5 算例分析

本算例采用北方某一典型孤立风光互补系统，系统包括100 MW光伏、100 MW风力发电，考虑到风光出力的随机性与不确定性，本文以1年8 760 h为考核时间段，采样时间为1 h。风光互补系统选取日负荷最高作为典型特征曲线如图3所示，最大负荷约为105 MW。储能单元选取目前比较流行的阀控铅酸电池作为优化对象，根据典型日数据分析及前文所提及的功率需求，本文选取储能系统最大充放电功率为50 MW。

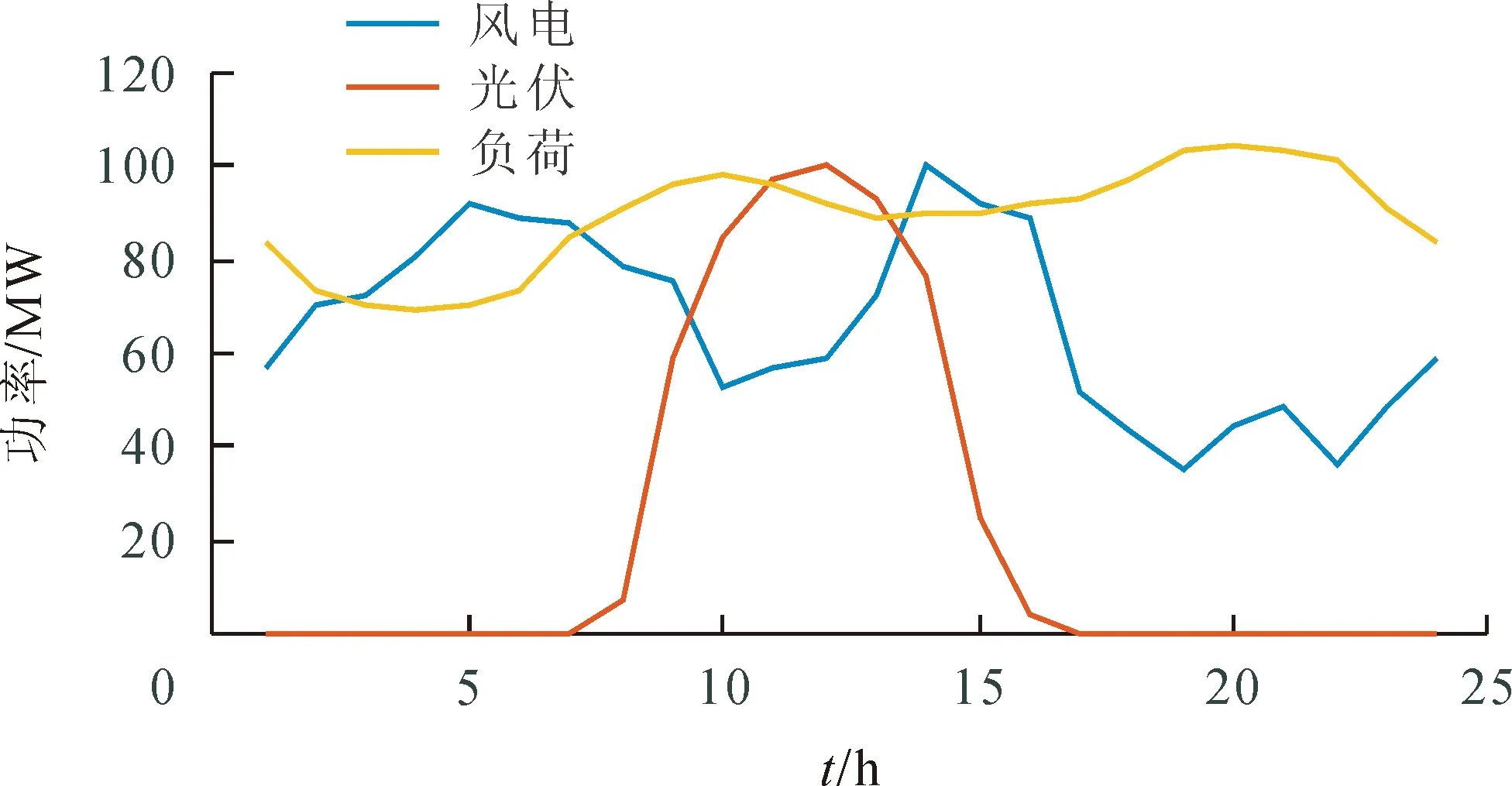
图3 风光互补系统典型日特性曲线

根据第一阶段的求解流程可以得到图4为负荷缺电率与图5新能源弃用率随储能容量增加的变化特性曲线，可以看出随着储能容量的增加负荷缺电率与新能源弃用率在逐步降低，表现出比较强的耦合关系。在微网建设中风光发电都与大电网相连，所以负荷缺电率并不会作为电站建设的重要指标，而在孤立风光互补系统中负荷缺电率可以作为评价系统可靠性的重要指标。根据工程实际新能源弃用率一般低于30%，本文选取0%～15%作为优化区间，对应的储能配置容量为120～360 MW。负荷缺电率越低系统稳定性越高，本文选取0%～10%为优化区间，对应的储能配置容量为220～400 MW。根据第一阶段在满足负荷缺电率与新能源弃用率的前提下所求得储能容量区间为220～360 MW，将其作为边界条件带入到第二阶段模型中，根据设定的目标函数求取最优储能容量配置。

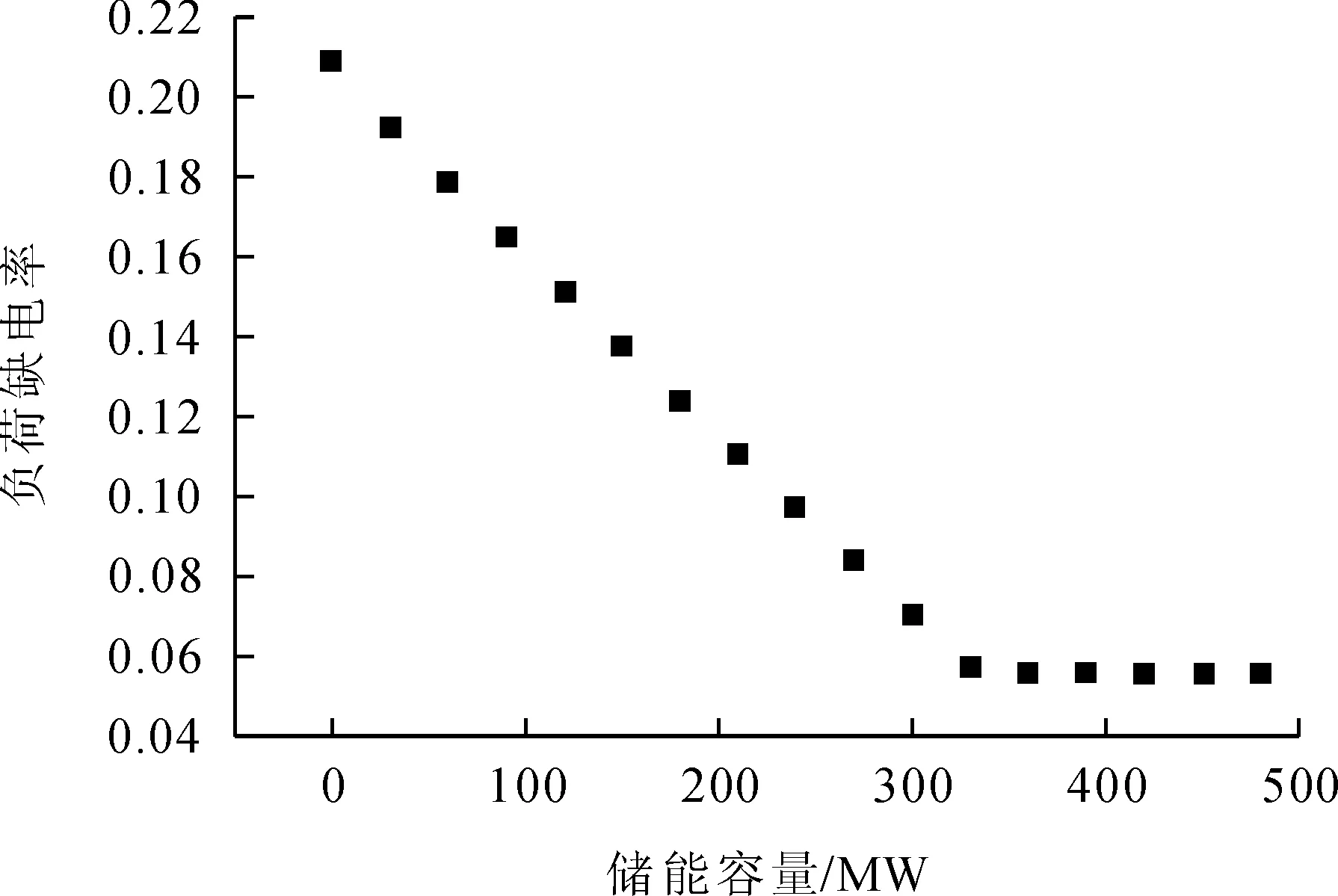
图4 负荷缺电率与储能容量特性曲线

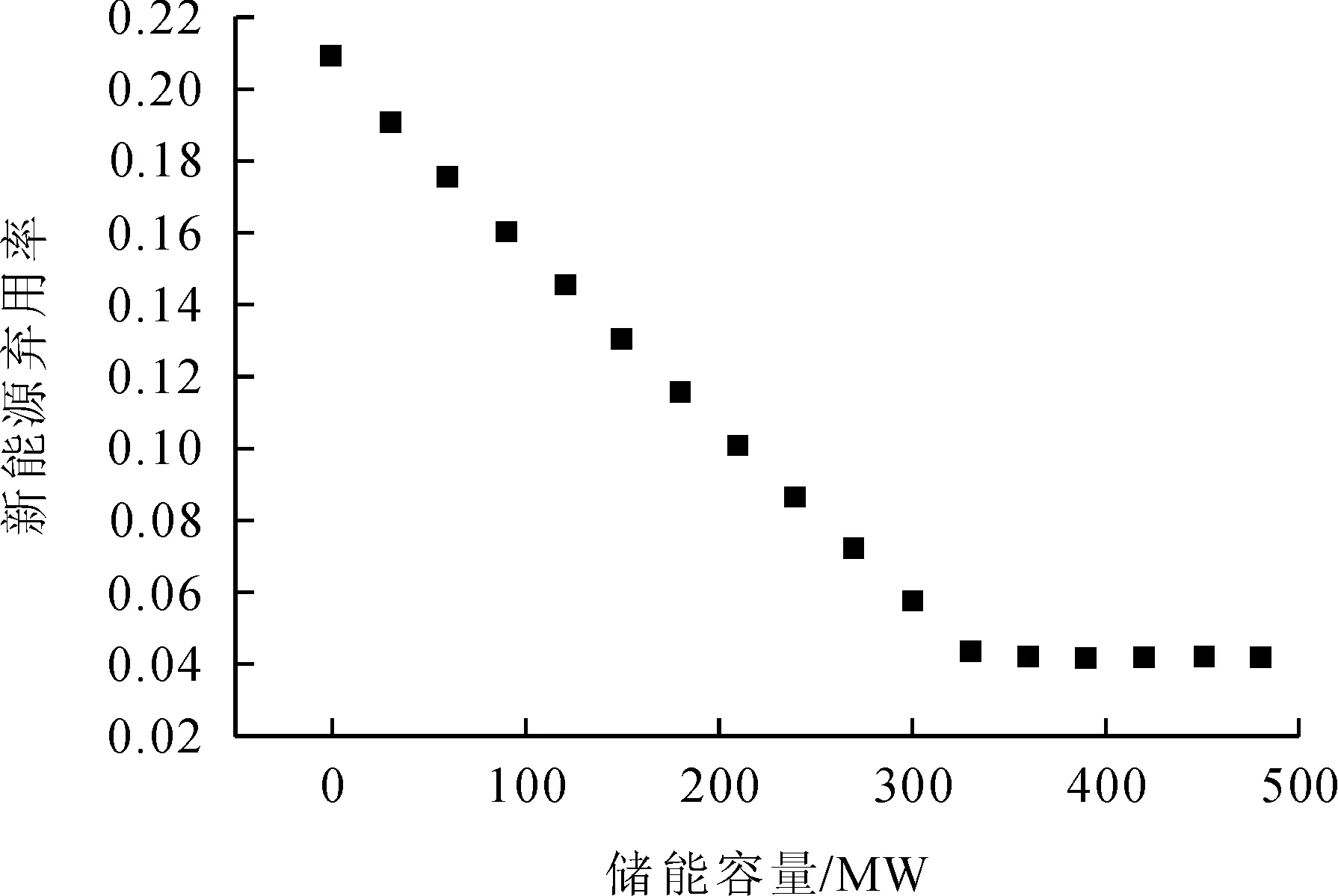
图5 新能源弃用率与储能容量特性曲线

根据第一阶段求得的储能容量范围，本文选取几个储能容量结合典型日负荷数据，其调度曲线如图6～图8所示。在没有配备储能单元时，风光互补系统在能源大发时会产生比较严重的弃风弃光现象。随着储能容量的增加，储能吸收部分能量以化学能的形式存储起来，减少了弃风弃光，当储能容量超过332 MW时，新能源下降率开始减慢直至不再变化。

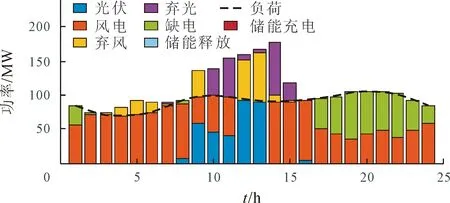
图6 储能为0 MW时系统调度曲线

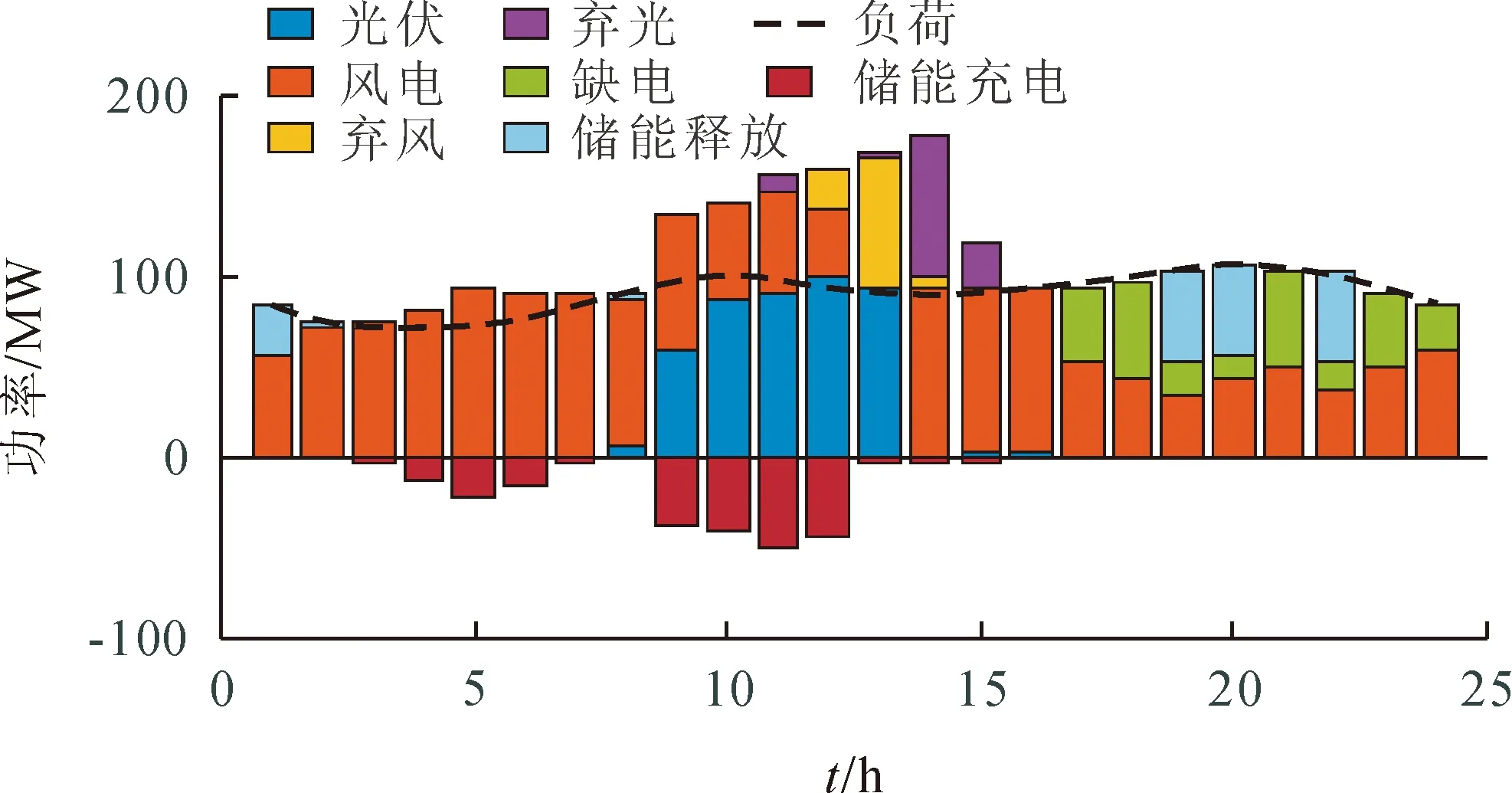
图7 储能为332 MW时系统调度曲线

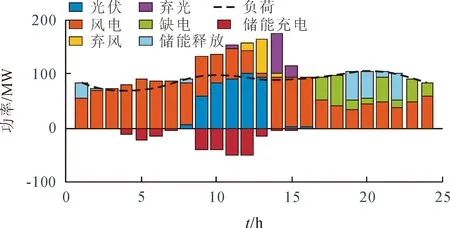
图8 储能为360 MW时系统调度曲线

第二阶段以年新能源弃用惩罚成本和储能初始投资年均成本最低为目标函数计算储能最优容量。本文拟采用储能系统使用年限为20年，储能容量单位成本为60万元/MWh。新能源弃用单位惩罚成本为350元/MWh。经过第二阶段的求解结果如表1所示。

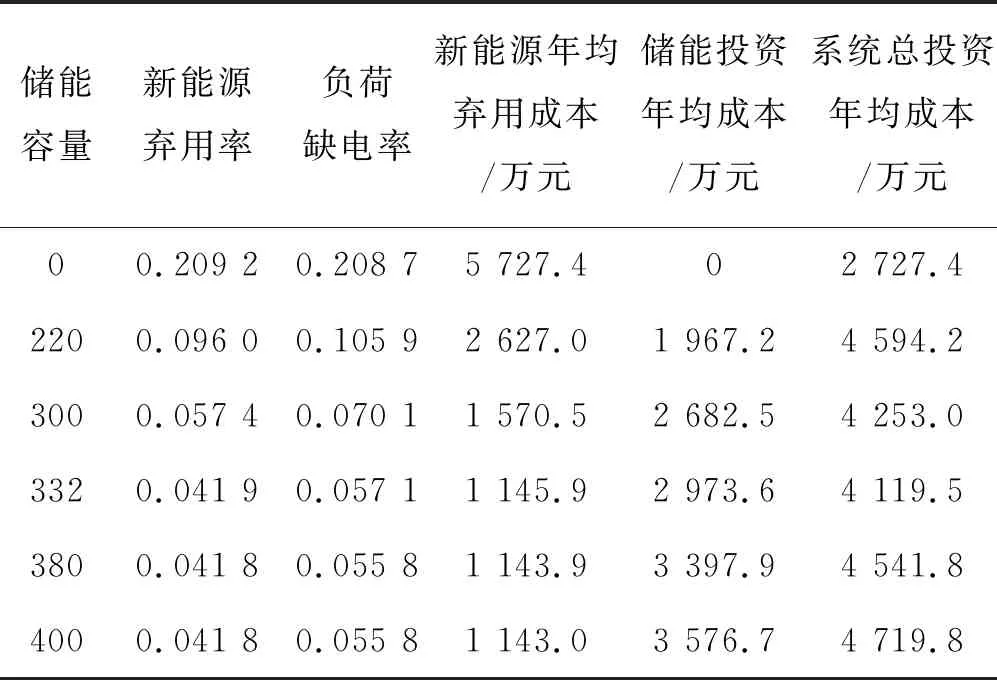
表1 不同储能容量系统投资成本情况

当储能容量为332 MW时，负荷缺电率与新能源弃用率也基本达到了最低，系统新能源弃用惩罚成本和储能初始投资年均成本最低。相比系统未增加储能时总成本下降了约1 607.9万元。由此可以发现在增加储能单元后，无论是在系统稳定性还是经济性上都得到了很大的提高。

6 结 语

本文提出以两阶段优化模型的风光互补系统储能容量配置优化方法，以负荷缺电率与新能源弃用率作为系统可靠性考核指标，以年新能源弃用惩罚成本和储能初始投资年均成本最低作为经济性指标，在兼具技术性与经济性的同时找寻风光互补系统最优储能容量。在研究案例中可以发现，通过合理配置储能容量可以降低负荷缺电率增加孤立风光互补系统的稳定性，同时可以降低15%左右的新能源弃用率。以总投资年均成本衡量系统的经济性，通过增加储能每年大约可以节约28%的投资成本。综上研究结果表明：

1)在满足负荷缺电率和新能源弃用率的同时存在最优储能容量配置，既可以提高风光互补系统的稳定性，也可以有效降低系统的投资成本；

2)负荷缺电率与新能源弃用率随储能容量的变化具有一定的耦合关系，在配置时需风光储能协同优化。