基于PSO-SVM算法的输电线路覆冰舞动预测模型

邹红波， 宋家乐， 刘 媛， 段治丰， 张馨煜， 宋 璐

(1.三峡大学 新能源微电网湖北省协同创新中心，湖北 宜昌 443000；2.三峡大学 电气与新能源学院，湖北 宜昌 443000)

架空输电线路在不均匀覆冰和随机风作用下会发生振幅约为5倍～300倍导线直径，频率约为0.1～3.0 Hz的振动，即驰振，也叫舞动。相对于微风振动和尾流诱发的振荡，舞动具有更强的破坏力，往往会导致金具磨损、闪络、断线等电力事故，进而引起大范围的停电事故。由于我国地形地势多变，气候复杂，很容易出现舞动事件，其中最严重的当属2008年的雪灾，北京、广东、云南等20个省(市、区)均受到不同程度影响，超出设计规范的冰厚使导线在随机风作用下大幅舞动，致使56万处杆塔倒塌，断线多达35万处，我国上亿人民深受其害。

为使电力系统免受舞动的影响，各国都对此进行了大量研究。

在覆冰舞动仿真领域，Diana等[1-3]采用有限单元法和准稳态理论模拟系统结构和再现流体弹性力来实现舞动模拟，并用现实案例进行验证，在此过程中采用了时域模拟及能量法，从工程的观点来看具有很好的效果。Cai等[4-7]采用Fluent软件在不同厚度新月形覆冰条件下模拟得到了四分裂导线的空气动力系数，并将有限元软件进行舞动仿真得出的结果与实际结果进行对比，发现二者具有较小的误差，证明了数值模拟确定的空气动力系数可用于研究架空输电线路的舞动特性和防舞技术。Zhou等[8-9]通过舞动场景模拟获得了分裂导线覆冰后的气动力系数，并以ABAQUS软件建立符合线路结构参数的模型，以自定义UEL模拟覆冰导线的气动力，取得了很好的成效。

在覆冰舞动预警领域，Yang等[10]通过构建RBF(radial basis function)网络模型进行预警。Zhang等[11-12]采用BP(back propagation)神经网络构建输电线路覆冰舞动预警模型，并通过十重交叉验证提高其预警准确性，使其更具使用价值。Wang等[13]则利用支持向量机(support vector machine，SVM)判断气象条件，当气象条件达到舞动条件后用AdaBoost分类器判断输电线路的档距、截面等确定是否发生舞动，即利用支持向量机和AdaBoost构成一个二级分类器进行预警。Lee等[14]采用Logistic回归模型进行预警，并用四重验证法和ROC(receiver operating characteristic)曲线判断模型的有效性。Cheng等[15-16]用BP、GA-BP(genetic algorithm-back propagation)、SVM等6种算法分别构建预警模型，并将效果最好的GA-BP和SVM采用方差-协方差权重动态分配法进行组合预测以达到更好的效果。程永峰等[17]则是用集成算法和SVM构成一个强分类器，且采用十重交叉验证对模型进行了优化。王津宇等[18]通过分析气象条件，提出包括风速、舞动时间等的风险系数并划分风险等级用以预警。徐文宝等[19]基于最优理论和模糊数学原理改进模糊层次综合评判法构建预警模型，且对舞动风险进行了等级划分，有利于工作人员做出相应举措。卢明等[20]通过加权灰色关联投影法筛选出多个相关度较高的影响因素作为输入提高预警准确率，并用随机森林算法进行预警。李清等[21]采用层次分析法计算出温度、冰厚、风速、导线截面积等指标的权重后用灰色聚类分析得到综合聚类系数，根据其判断舞动状态。鉴于舞动数据的保密性，难以获得大量的真实数据对舞动进行预警，因此考虑有限元仿真模拟真实舞动，在尽量多的因素下对舞动进行仿真获取足够多的数据构成数据集，然后进行舞动预警。

本文利用有限元软件仿真模拟了LGJ-400/50型号线路在不同档距、风速等状态下的动态响应，得到不同参数下导线是否舞动的数据集。进而根据模拟获得的数据集和PSO-SVM(particle swarm optimization-support vector machines)算法构建预警模型，将档距、风速、初始风攻角作为模型的输入，覆冰导线是否舞动作为输出，该模型具有很高的有效性及实用性，对于输电线路覆冰舞动预警具有一定的价值。

1 覆冰四分裂导线舞动模拟

1.1 覆冰导线数值模型的建立

进行覆冰舞动模拟时，气动力是一个很重要的因素，本文利用Fluent软件模拟获得四分裂导线的气动力系数，冰形为新月形，冰厚为12 mm，导线型号为LGJ-400/50，半径为13.8 mm，子导线间距为450 mm，导线模型如图1所示。导线模型在gambit软件中建立，流场区域设置为2 m×2 m大小，划分网格时选择非结构化网格，覆冰四分裂导线二维建模结果如图2所示。

图1 导线模型(mm)

(a) 整体网格

利用Fluent软件进行仿真模拟时采用瞬态分析，求解器设置为simple算法、spalar-allmaras模型、二阶隐式求解，时间步长为0.001 s，时间步数为200，风攻角α按逆时针方向从0°～180°每隔10°模拟一次。

1.2 气动力系数随攻角的变化规律

导线所受气动力升力FL、阻力FD及扭矩FM分别由对应的系数CL,CD,CM计算得到

(1)

式中：ρ为空气密度,为1.225 kg/m3;D为导线直径，为27.6 mm;V为风速，为12 m/s。

式(1)中的气动力系数CL，CD，CM由1.1节可得，图3显示了攻角变化过程中气动力系数的变化规律，经过与风洞试验结果[22]对比，符合实际，故可用于舞动仿真。

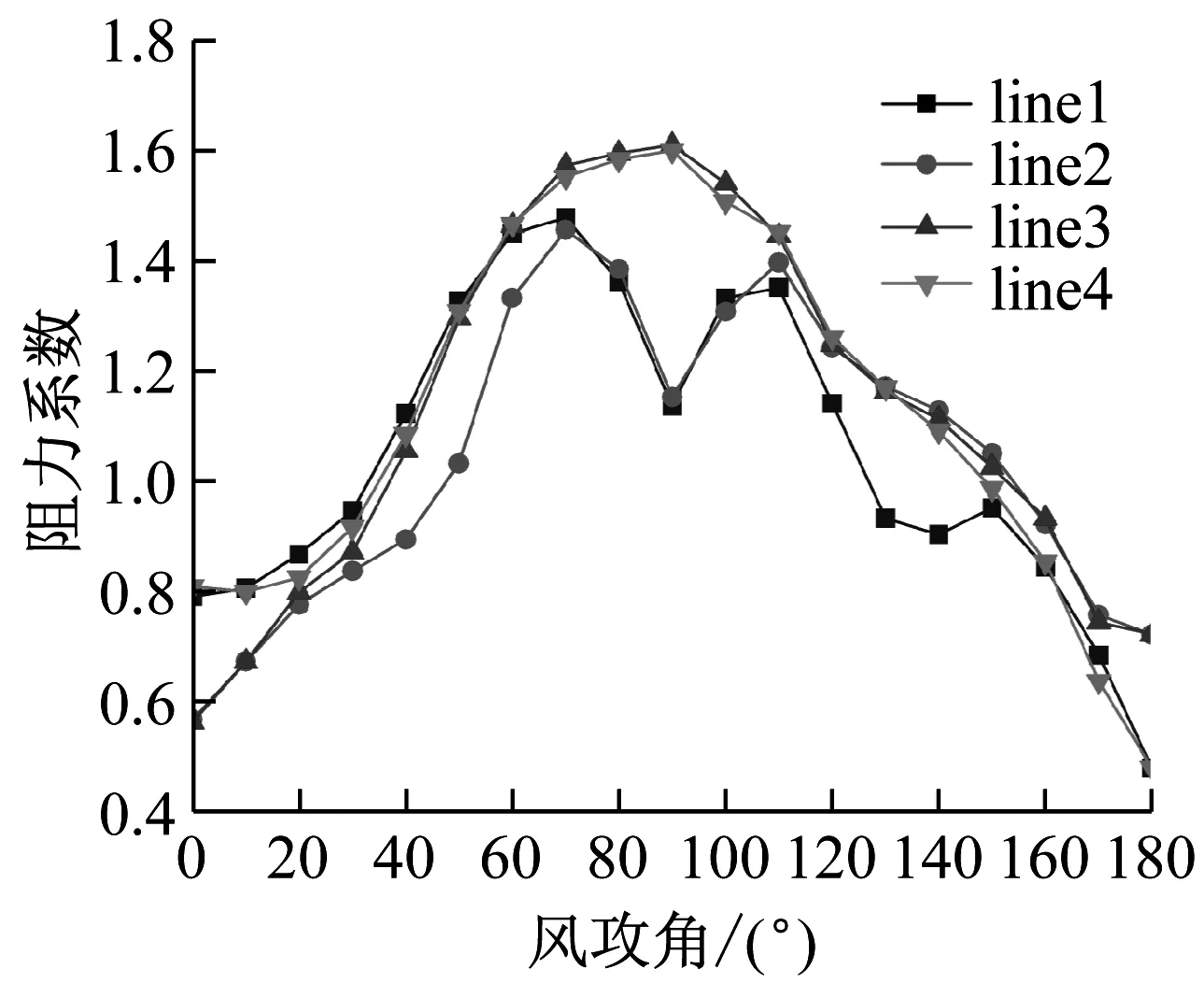
(a) 阻力系数

当风攻角α=0°时，子导线2，3分别受子导线1，4尾流的影响，阻力系数小于子导线1，4；当α=90°时，覆冰导线迎风面积达到最大，同时尾流效应也达到最大，处于尾流区的子导线1，2阻力系数大幅下降；同理，当α=180°时，处于尾流区的子导线阻力系数有所下降。各子导线的升力系数随攻角改变的变化曲线整体呈波状，当α=0°，α=90°，α=180°时，各子导线升力系数为0。各子导线扭矩系数在攻角α为0°，110°及180°时等于0，扭矩系数基本不受尾流的影响，各子导线的扭矩系数随攻角的变化规律相同。

由于间隔棒的存在，分裂导线各子导线的舞动表现为一个整体，因此需要定义四分裂导线的整体气动力系数分别为CL(t),CD(t),CM(t)

(2)

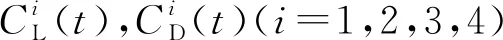
(3)

整体气动力系数由式(2)、式(3)计算得出，其随攻角的变化规律如图4所示。

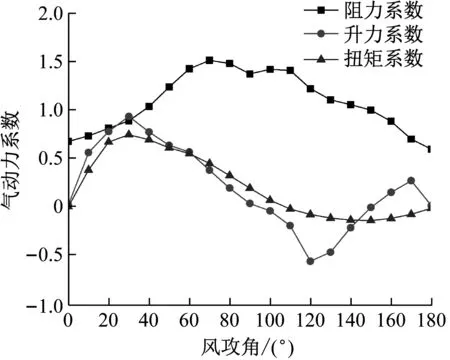
图4 四分裂导线整体气动力系数随风攻角变化的曲线图

1.3 覆冰导线的气动激励

经由1.1节和1.2节可得到导线所受气动力，如图5所示(z为横向，y为竖直)。

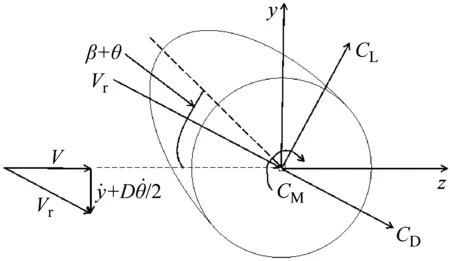
图5 覆冰导线受力及风攻角示意图

t时刻覆冰导线单元节点上受到的气动力载荷可由式(4)计算得到

[Fy(t)Fz(t)FM(t)]T=

(4)

式中：Fy(t)，Fz(t)分别为导线单元节点在竖直方向和横向受到的气动力载荷;Cy(t)，Cz(t)为相应的系数;CM(t)如公式(2)所示。Cy(t)，Cz(t)计算公式如式(5)所示

(5)

t时刻的风攻角α可由式(6)计算得到

(6)

1.4 覆冰导线有限元模型的建立

本文使用APDL语言建立有限元模型，本模型考虑到导线的平动自由度和转动自由度共包括4个自由度，因此导线和间隔棒均用beam188单元进行模拟，且为保证结果的准确性，导线采取0.5 m一个单元进行建模，覆冰四分裂导线有限元模型如图6所示。

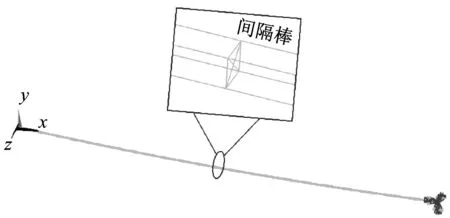
图6 200 m档距四分裂导线有限元模型

1.5 随机风作用下的覆冰四分裂导线舞动特性

1.5.1 不同风速的影响

基于以往研究成果，舞动发生的风速条件为4～25 m/s，且在高风速时舞动幅值会有明显的降低。当风攻角为90°，档距为200 m时，不同风速下模拟得到的竖直方向舞动幅值(舞动以竖直方向为主)与风速的关系如图7所示。

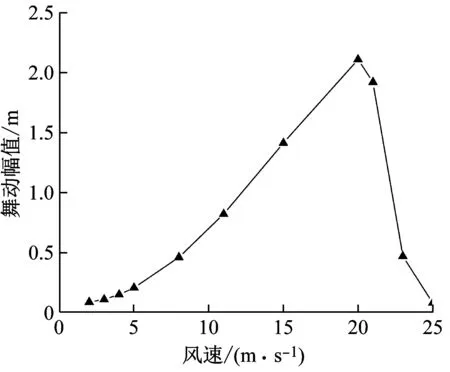
图7 四分裂导线舞动幅值数随风速变化的曲线图

由图7可知，当风速达到4 m/s时覆冰四分裂导线达到舞动条件，舞动幅值开始增大，当风速达到20 m/s时覆冰四分裂导线舞动幅值开始大幅下降，与实际情况相符。

1.5.2 不同档距的影响

为明确档距对覆冰导线舞动幅值的影响规律，分别模拟得到了风攻角为90°，风速为12 m/s，档距为200 m,300 m,500 m时的竖直方向舞动幅值，变化规律如图8所示。

图8 四分裂导线舞动幅值数随档距变化的曲线图

由图8可知，在档距增大的同时，舞动幅值也会增大，故在舞动高风险区应减小线路档距以降低舞动风险。

2 输电线路覆冰舞动预警模型

2.1 支持向量机的原理

支持向量机[23]实质上是构造一个超平面，使映射到高维特征空间样本数据集中的支持向量与超平面的距离最大化，同时相关的计算在低维空间中进行的一种算法。将超平面的法向量和截距定义为ω，b，可得到SVM分类模型优化问题

(7)

式中:ξi为松弛变量;C为惩罚因子，通过拉格朗日乘子α={α1,…,αN}和μ={μ1,…,μN}得到其拉格朗日函数为

(8)

进而可得到优化问题的对偶问题为

(9)

以径向基函数作为内核可得到其分类决策函数为

(10)

式中：z为核函数中心;σ2为方差。

2.2 基于粒子群优化算法的SVM参数优化

本文采取径向基函数作为SVM的核函数，利用粒子群优化算法PSO对其惩罚参数c和核函数参数g进行优化[24-26]，优化过程中按式(11)对粒子的速度、位置进行更新

(11)

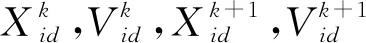
利用粒子群优化算法优化SVM的流程图,如图9所示。

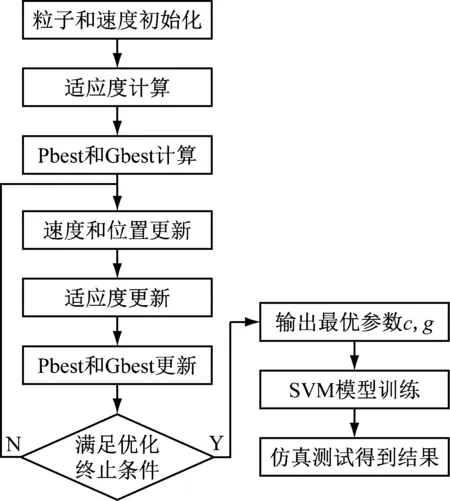
图9 PSO优化SVM流程图

2.3 四分裂导线覆冰舞动预警

基于PSO-SVM算法的四分裂导线覆冰舞动预警流程，如图10所示。

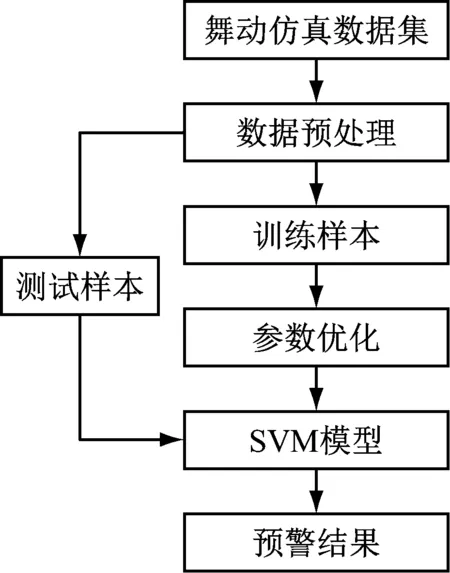
图10 预警流程图

步骤1仿真得到1 539条数据如表1所示，随机分别选取70%的舞动数据和非舞动数据共1 077条作为训练数据，保证足够的数据量，增大模型的预测精度。

表1 舞动数据集

步骤2由于输入变量档距、风速和初始风攻角的数量级不同，需要将样本数据归一化以保证预测结果的准确度，本文采用的归一化范围为[0,1]，归一化公式为

(12)

式中:x0,x为归一化前后的数据值;xmax,xmin为待归一化数据中的最大值与最小值。

步骤3利用PSO得到SVM最佳的惩罚参数c为11.473 1和核函数参数g为1.070 1，然后构建SVM覆冰舞动预警模型。

步骤4将步骤1中划分的余下的462条作为测试数据输入到模型中，确定PSO-SVM模型的舞动识别准确度。

不同算法的预测结果对比如表2和图11～图12所示，PSO-SVM模型对于舞动的识别准确度高达98.48%，与其他算法构建的模型比起来具有更高的正确率，对覆冰舞动预警更加具有参考意义。

表2 不同分类算法准确度对比

(a)

图12 输电线路覆冰舞动预测误差

3 结 论

本文利用有限元软件ANSYS仿真模拟了LGJ-400/50型号线路在不同档距、风速、等状态下的动态响应，得到了覆冰四分裂导线是否舞动的数据集，并通过PSO-SVM算法构建预警模型，后将预警结果与BP、SVM、GA-SVM模型预警结果进行对比验证了其准确性及有效性，证明了该模型在结合线路结构参数、环境参数、覆冰在线监测数据等输入参数后可以实现输电线路覆冰舞动预警，具有一定的参考意义。