基于动力吸振原理的低频多模态抑振器设计

程一鹏， 彭子龙， 温华兵， 宋 昊， 郭有松

(1.江苏科技大学 能源与动力学院，江苏 镇江 212100；2.中国船舶工业系统工程研究院，北京 100036；3.常州工邦减振设备有限公司，江苏 常州 213000)

舰船运行过程中，动力设备及管路的振动通过基座、舱壁等结构向船体及舱室传递，严重影响舒适性。对于军用舰船，艇体振动引发的声辐射还会降低其隐蔽性能，削弱其作战能力。机械运转导致的振动以低频振动为主，而低频振动波长较长，工程实际中难以进行控制，从而成为振动与噪声控制领域的一大难题。动力吸振(dynamic vibration absorber，DVA)原器自身的频率选择特性使其在低频振动控制领域应用广泛，通过调节参数，理论上可以实现任意频率振动的控制。经过数十年的发展，动力吸振器的振动控制方式由最初的被动控制[1-3]逐渐过渡为半主动控制[4-6]、主动控制[7-9]，控制效果提升的同时，内部结构也更为复杂，安装及维护成本更高，难以大规模应用于工程实际中，因此被动控制依然是当前动力吸振器的主流设计方向。

舰船作为连续体，其低频振动响应含有大量共振峰，分别对应多个模态，单自由度动力吸振器只能针对其中一个共振峰进行抑制，而多重动力吸振器(multiple dynamic vibration absorber, MDVA)为多个单自由度吸振器的组合，因此具有多模态特性，通过调节其参数使MDVA的模态频率与被控对象模态频率相对应，即可对多个共振峰进行抑制。

悬臂梁式动力吸振器由于结构简单、工程实用性强而成为传统被动式动力吸振器的主要结构形式。周荣亚[10]将悬臂梁式动力吸振器等效为具有多频吸振特性的复式动力吸振器，然而利用悬臂梁自身模态进行振动控制的效果有限，虽然能够实现多频减振，但不能有效地调频，不适合实际工程应用。为此陈文华等[11]以频率可调、可多频吸振为目标，提出一种适用于手持打磨工具的悬臂梁式动力吸振器，然而该吸振器只能适用于小型抑振对象，大型结构的模态频率较低，必然要求抑振结构向大质量、大尺寸变化，悬臂梁式动力吸振器受其本身几何结构限制无法满足上述要求。

采用橡胶作为隔振、吸声和冲击防护的弹性元件已有50多年的历史。随着工业技术的发展，在振动工程、声学方面和瞬态冲击实践等领域中，对于橡胶的应用尤其不容忽视[12]。圆柱体、圆板在不同边界条件下的固有振动特性已有大量研究[13-16]，将这些简单结构按照一定规律进行组合后，就会达到与吸振器相同的抑振效果，该组合体称为抑振器。王钰杰等[17]研究了低频抑振器材料和结构参数对水中薄板振动声辐射的影响，然而该抑振器结构设计没有理论基础，且未考虑板的振动特性，因此其抑振机理尚有欠缺。马建刚等[18]提出一种基于动力吸振原理的多带隙局域共振抑振器，并通过实验和理论计算验证了该结构对梁的振动控制效果，而板结构模态更为复杂，抑振结构需针对其模态重新设计，抑振效果有待进一步研究。

本文基于动力吸振原理，以橡胶和钢为主要材料，设计了一种低频多模态抑振器，从理论上计算了其各部分的等效刚度与等效质量，并以吸振器参数为基准对抑振器各组成部分的材料参数和几何参数进行调整，进而以一四边简支板为控制对象，通过仿真和实验验证了抑振器的振动控制效果。

1 理论分析

1.1 阻抗特性

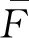
图1 多重动力吸振器模型

以动力吸振器为对象建立力学平衡方程

(1)

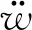
(2)

1.2 振动特性

对于杨氏模量为E，密度为ρ，泊松比为σ，厚度为h的薄板，其受迫振动方程为

F0δ(x-x0)δ(y-y0)eiωt

(3)

式中:D为薄板的弯曲刚度;w为板的横向位移;F0为点激励力;δ(·)为狄拉克函数。将w(x,y,t)以模态位移叠加的形式表示出来

(4)

将式(4)代入式(3)，得到以模态位移表示的振动方程

D∇4φTη-ρhω2φTη=F0δ(x-x0)δ(y-y0)

(5)

式中，Φ,η分别为振型函数向量和模态位移向量，φ=[φ11,φ12,…,φmn]T，η=[η11,η12,…,ηmn]T，对式(5)等号两边同乘Φ并沿板面积分，可得到

D∇4∬SφTφηds-ρhω2∬SφTφηds=F0φ(x0,y0)

(6)

其中，振型函数φ满足以下振型方程

(7)

将式(7)代入式(6)可得到矩阵形式平板受迫振动方程

(K-ω2M)η=P

(8)

式中:K=ρhΩ2∬SφTφηds,M=ρh∬SφTφηds分别为刚度矩阵和质量矩阵;Ω为固有频率矩阵;P=F0φ(x0,y0)为激励矩阵。通过式(8)可以得到模态位移表达式

η=P/ρh(Ω2-ω2)φTφ

(9)

将式(9)代入式(4)即可得到平板横向位移表达式。本文以长、宽分别为0.32 m，0.24 m的四边简支板为控制对象，在(0.08,0.08)位置处受到单位载荷力激励，则其振动响应频响曲线如图2所示。

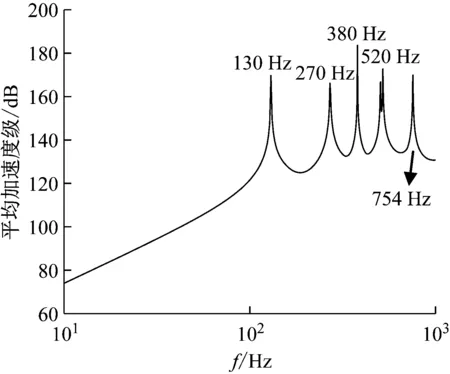
图2 平板振动响应频响曲线

板附加4×4吸振器阵列模型示意图，如图3所示。在动力吸振器设计过程中，取动力吸振器基础振子质量m1=0.2mf，次级振子m2=m3=m1/3，其中基底质量mf=ρhab，a,b分别为吸振器阵列在x,y方向的间距。对于附加吸振器阵列平板，其受迫振动方程为

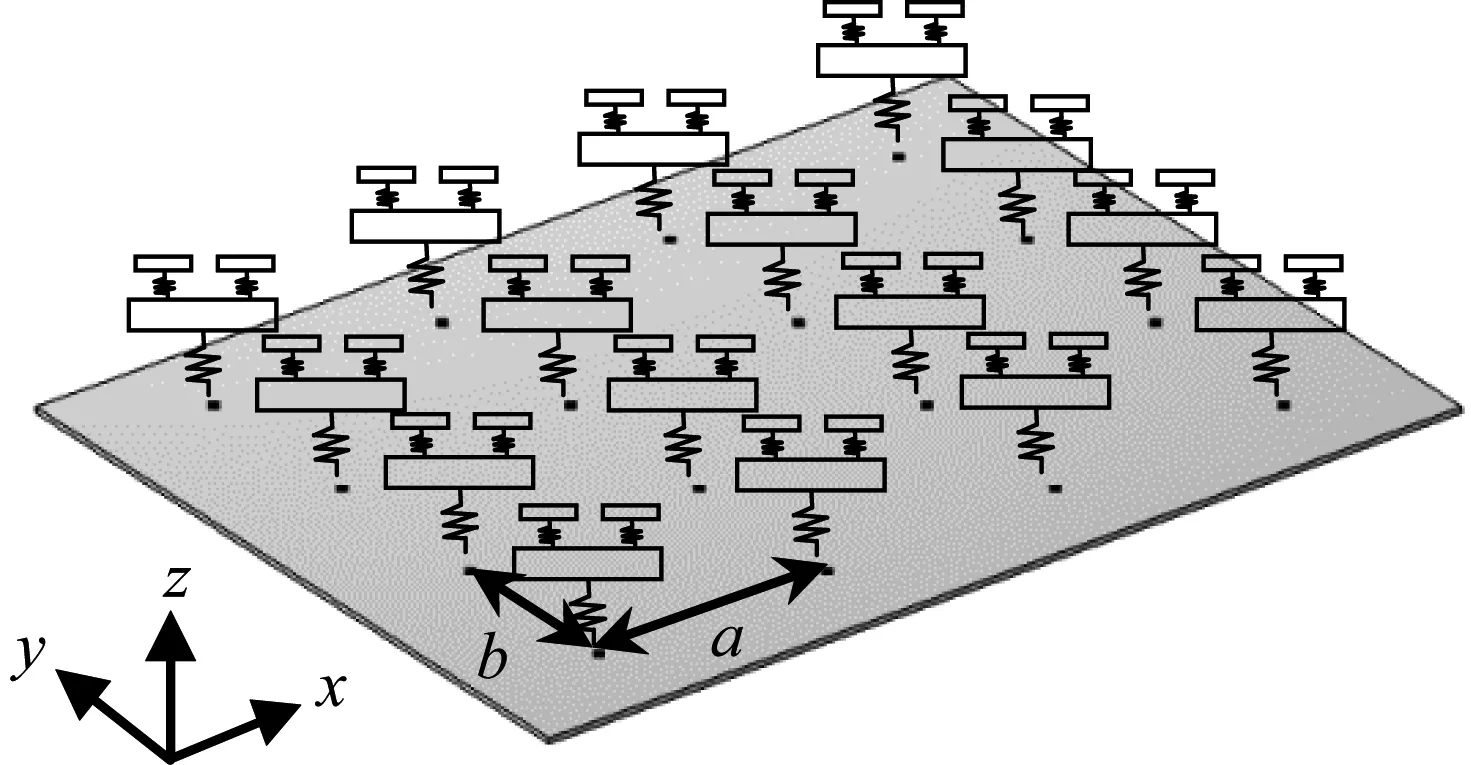
图3 板附加多重动力吸振器阵列模型

(10)

式(10)等号右端第二项中Fj为各动力吸振器对板的反作用力，根据力与阻抗关系F=Zw，代入式(10)可得到

F0δ(x-x0)δ(y-y0)

(11)

式(11)同样可以表示为矩阵形式振动方程

(12)

图1所示动力吸振器模态频率方程为

(13)

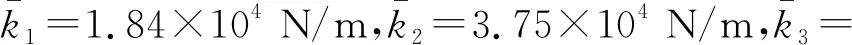
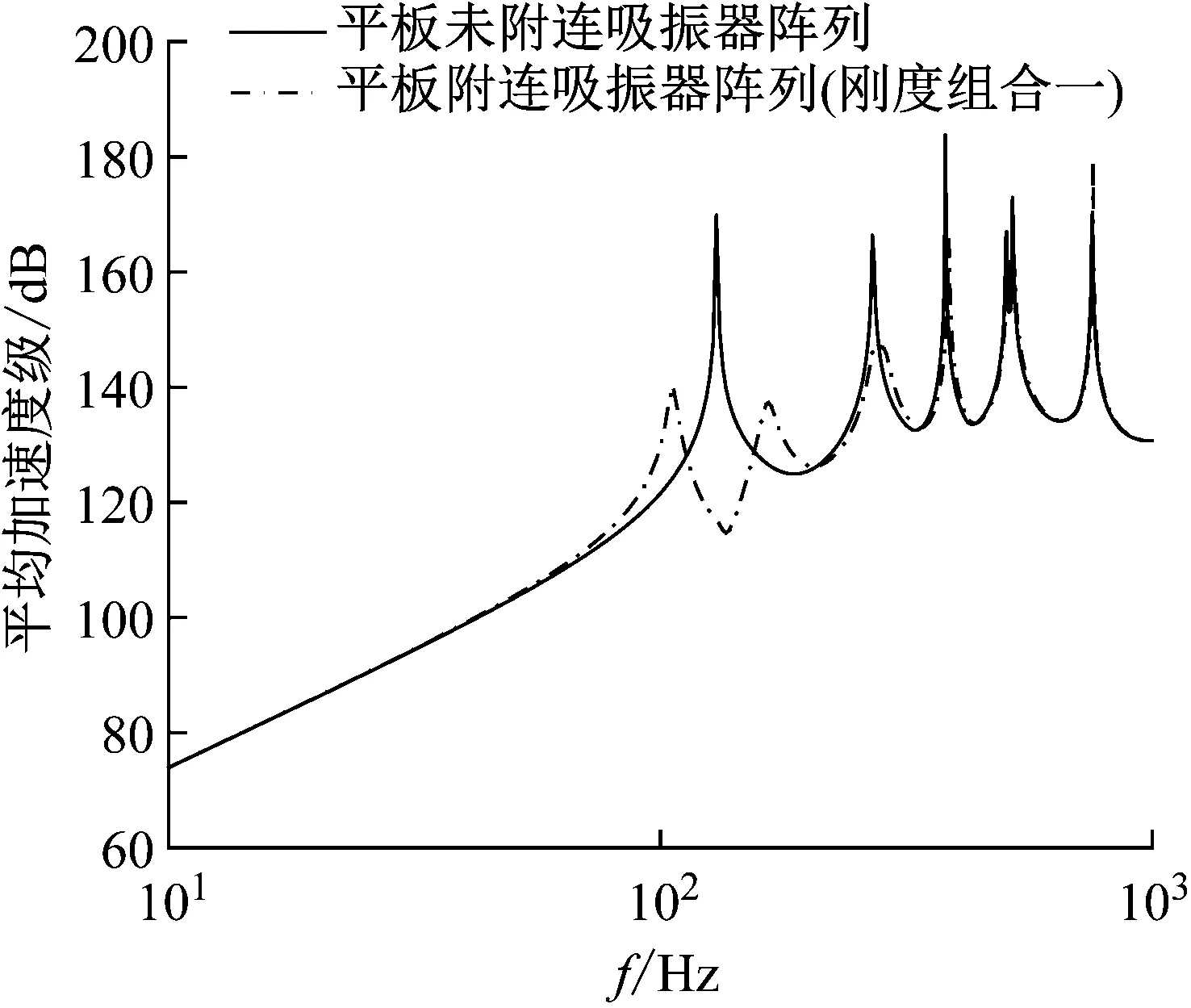
图4 吸振器阵列振动控制效果(刚度组合一)

由图4可知，将刚度组合一作为吸振器参数无法满足多共振峰的抑制要求，多重动力吸振器仅有一个吸振模态被激发出来，进一步将通过求解集中质量m1的位移传递率曲线以解释该现象。由式(2)可得位移传递率T的表达式为

(14)

式(14)中，令无量纲频率γ=ω/ω1为横坐标，其中ω1为吸振器第一阶固有频率，不同阻尼比下基础振子位移传递率频响曲线如图5所示。

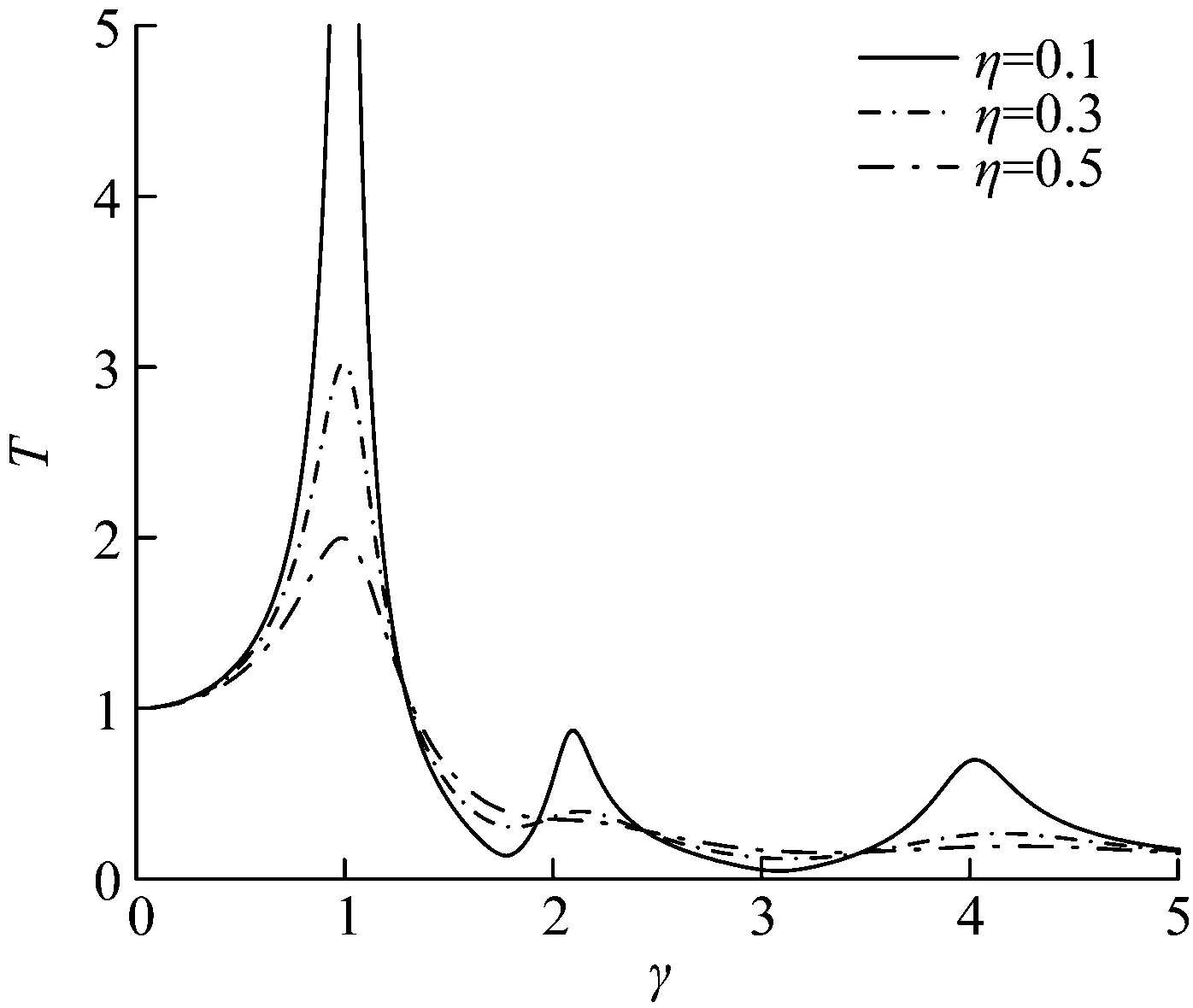
图5 基础振子位移传递率频响曲线(刚度组合一)

由图5可知，在γ=1时位移传递率最大，而在高频时位移传递率均小于1，因此m1-k1构成了隔振系统，振动很难传递到质量块m2,m3，因此吸振器的第二阶、第三阶吸振模态并未被激发。

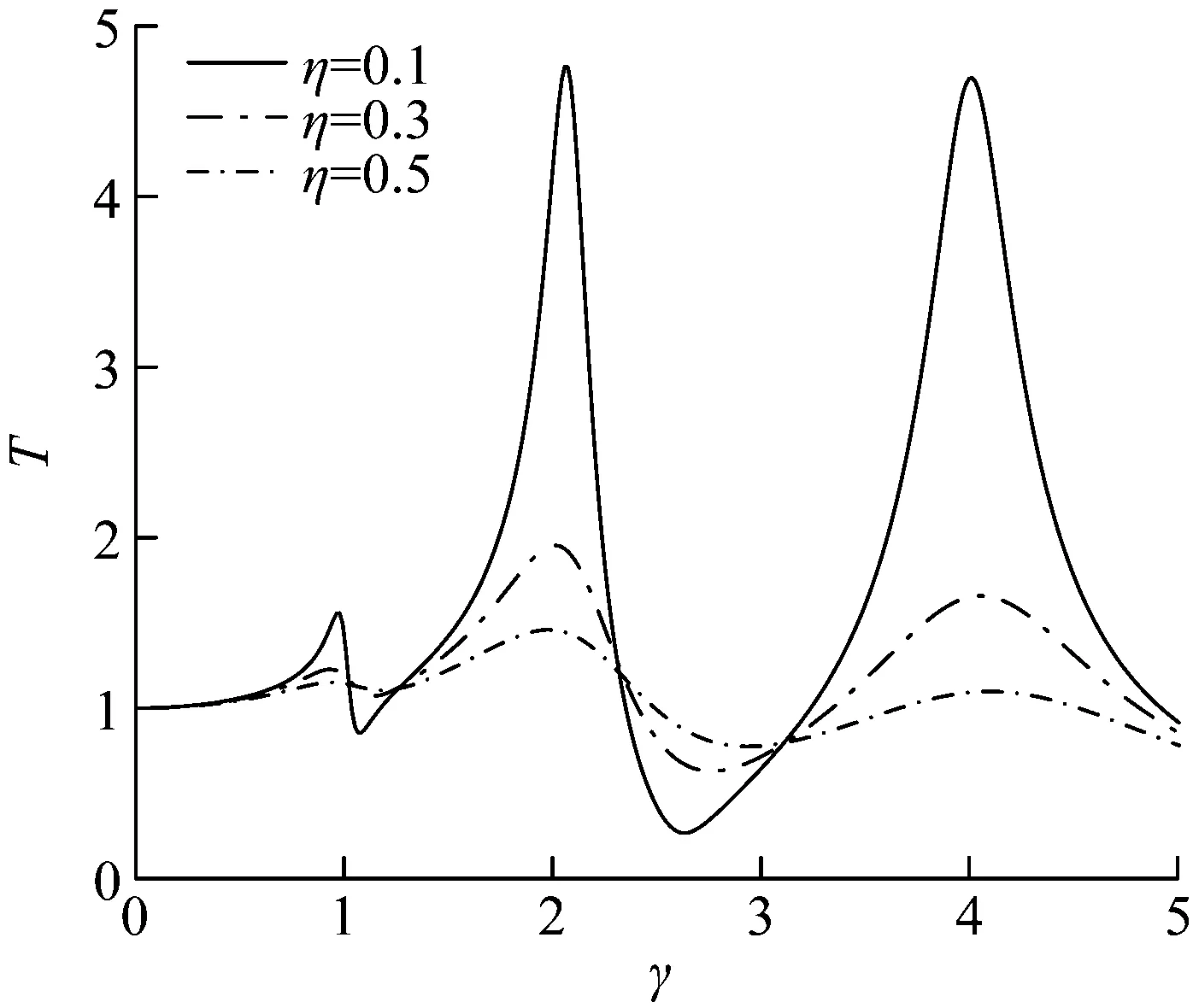
图6 基础振子位移传递率频响曲线(刚度组合二)

由图6可知，将刚度组合二作为吸振器参数后，3阶共振频率处位移传递率均大于1，振动可以传递到m2,m3上，因此吸振器第二阶、第三阶吸振模态可以被激发出来，可以对多个共振峰进行抑制。

将最终确定的动力吸振器参数mi,ki代入式(2)，然后将得到的阻抗代入式(12)，得到附加吸振器阵列前后的平板振动响应频响曲线如图7所示，可以看出板在附加所设计的多重动力吸振器阵列后选定频率的峰值响应有明显下降，因此在设计多模态低频抑振器时将以多重动力吸振器的参数mi,ki作为参考，进而确定其各组成部件的几何参数和材料参数。

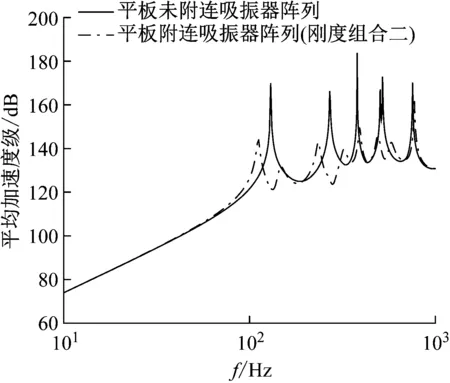
图7 吸振器阵列振动控制效果(刚度组合二)

2 多模态低频抑振器结构设计

为达到与第1章动力吸振器阵列相同的抑振效果，多模态低频抑振器需以多重动力吸振器参数mi,ki(i=1,2,3)为基准进行设计，其初步设计模型如图8所示。模型主要组成部分为：基底橡胶、金属柱壳、橡胶板、质量块。其中基底橡胶、中间橡胶板和顶部橡胶板用于提供刚度和阻尼，并分别对应k1,k2,k3；金属柱壳、质量块用于提供质量，并分别对应m1,m2,m3。

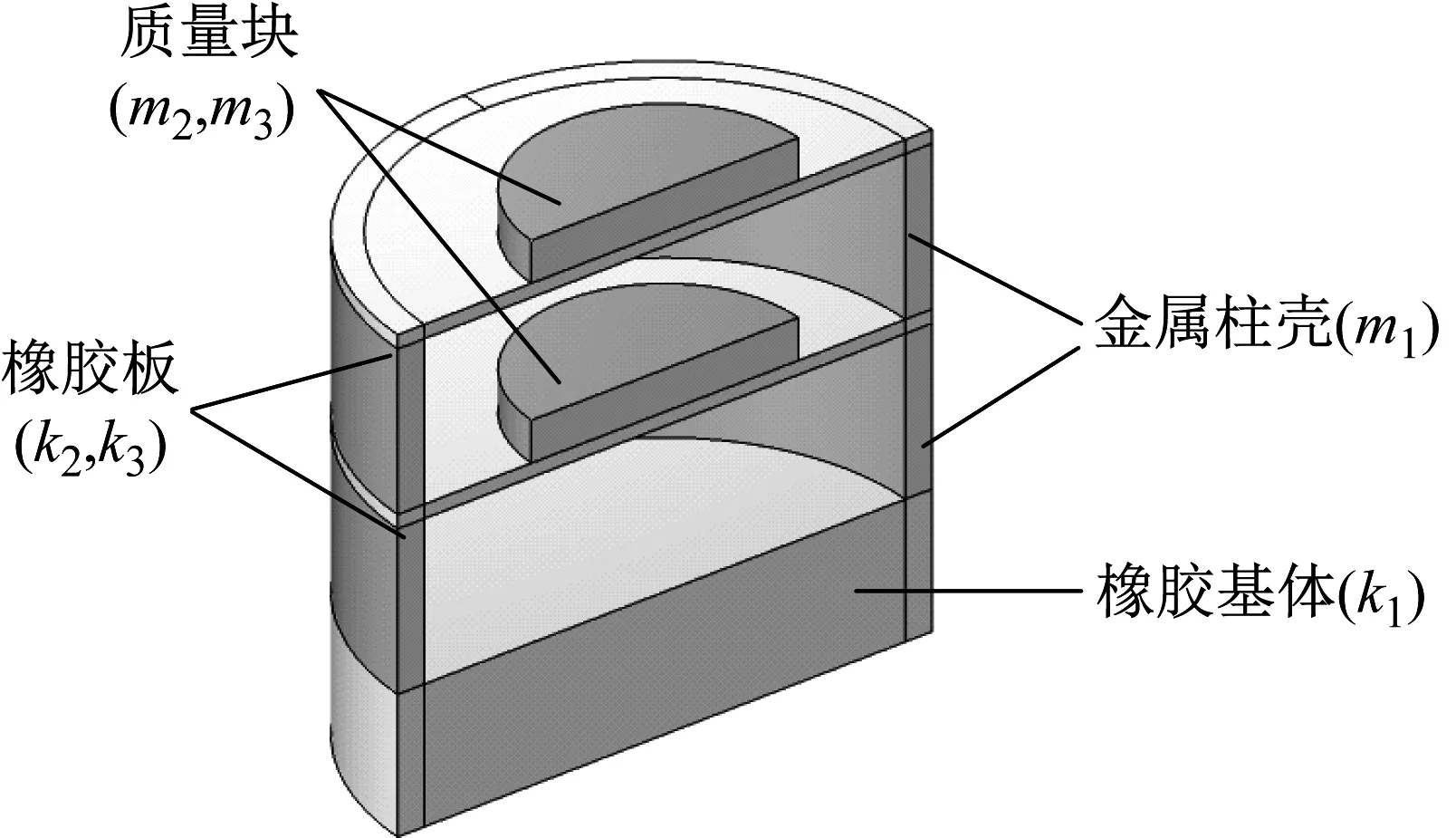
图8 多模态低频抑振器初步设计模型

2.1 橡胶板-质量块结构设计

圆板固有振动基本方程[19]为

(15)

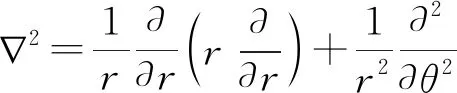
w(r,θ,t)=W(r,θ)eiωt

(16)

将式(16)代入式(15)得到振型方程

(∇4-k4)W=0

(17)

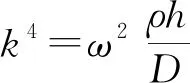
(18)

对于中心附加一定体积质量块的周界钳定圆板，设其半径为a，质量块半径、高度、密度分别为b,h0,ρ0，则其边界条件可以表示为

(19)

式中:mb为附加质量;Vr为Kirchhoff剪切应力。将式(18)代入式(19)并令m=0，可以得到关于Am,Bm,Cm,Dm的齐次线性方程组，令其系数行列式为零可以得到基频系数μ0，由此可以求得对应纵向位移模态的基频

(20)

周边固定中心附加质量块圆板振动的基频也可以用等效刚度keq和等效质量meq来表示

(21)

联立式(20)、式(21)可以在给定等效刚度、等效质量后确定板的杨氏模量

(22)

对于初步设计模型，橡胶圆板周边被金属圆柱壳固定，柱壳厚度不可忽略不计，因此圆板边界条件并非理想周界钳定条件，因此无法应用前述理论推导计算其固有频率。进一步观察发现，圆板周界被一定厚度圆柱壳固定时，其周界边界条件可以做如下近似

(23)

式中,δ为圆柱壳厚度。式(19)中前两个边界条件替换为式(23)即可完成对周界被一定厚度圆柱壳固定的圆板的特征频率求解。仿真验证结果如图9所示。

(a) 实际边界条件(f=164.19 Hz)

通过理论计算得到的质量块-圆板在图9(b)对应边界条件下的固有频率为162.37 Hz，相对误差为1.1%，因此可以应用理论推导较准确的计算周界被金属柱壳固定圆板的固有频率。

通过式(23)对边界条件做近似处理时，其前提条件为圆板上下面均被柱壳固定，图8中腔内橡胶板满足该条件，然而顶部橡胶板仅有下表面被柱壳固定，因此为使顶部橡胶板同样可以满足式(23)的近似边界条件，需从与其下表面相连的柱壳中取出一部分压在上表面，从而达到上下表面均被柱壳固定的条件，取出的柱壳部分高度与柱壳厚度相等即可。

2.2 橡胶基体-金属柱壳结构设计

本文初步设计的低频抑振器其橡胶基体为一柱状弹性体，其等效刚度可表达为

(24)

式中:E,S,h分别为柱状弹性体的杨氏模量、横截面积和高度;mn=f(n)为形状系数，n=Sl/Sf，Sl和Sf分别为柱状弹性体的约束面积和自由面积，考虑到n的不同取值，mn有以下表达式

(25)

柱状弹性体上附加等半径柱状质量块后，整体结构的轴向共振模态特征频率为

(26)

将柱状弹性体视为含质量弹簧，则等效质量meq=m1+m2/3，m1为质量块质量，m2为柱状弹性体质量，keq为柱状弹性体的等效刚度。

若直接将金属圆柱壳置于橡胶基体之上，由于金属柱壳与橡胶基体的接触面只占据橡胶基体横截面的很小一部分，因此与等质量圆柱体质量块置于橡胶基体的情况相比，金属柱壳置于橡胶基体上改变了橡胶基体的受力条件，两种情况并不能等效。为了能够应用理论推导计算柱状弹性体上附加圆柱壳结构的轴向共振模态特征频率，必须使圆柱壳下表面与橡胶基体全接触，因此圆柱壳需要增加底层，该底层厚度与圆柱壳厚度保持一致即可，有限元验证结果如图10所示。

由图10可知，圆柱壳增加底层后，整体的特征频率与等质量匀质柱状质量块置于橡胶基体的特征频率相等，因此两种情况等效。根据式(24)，则橡胶基体的杨氏模量为

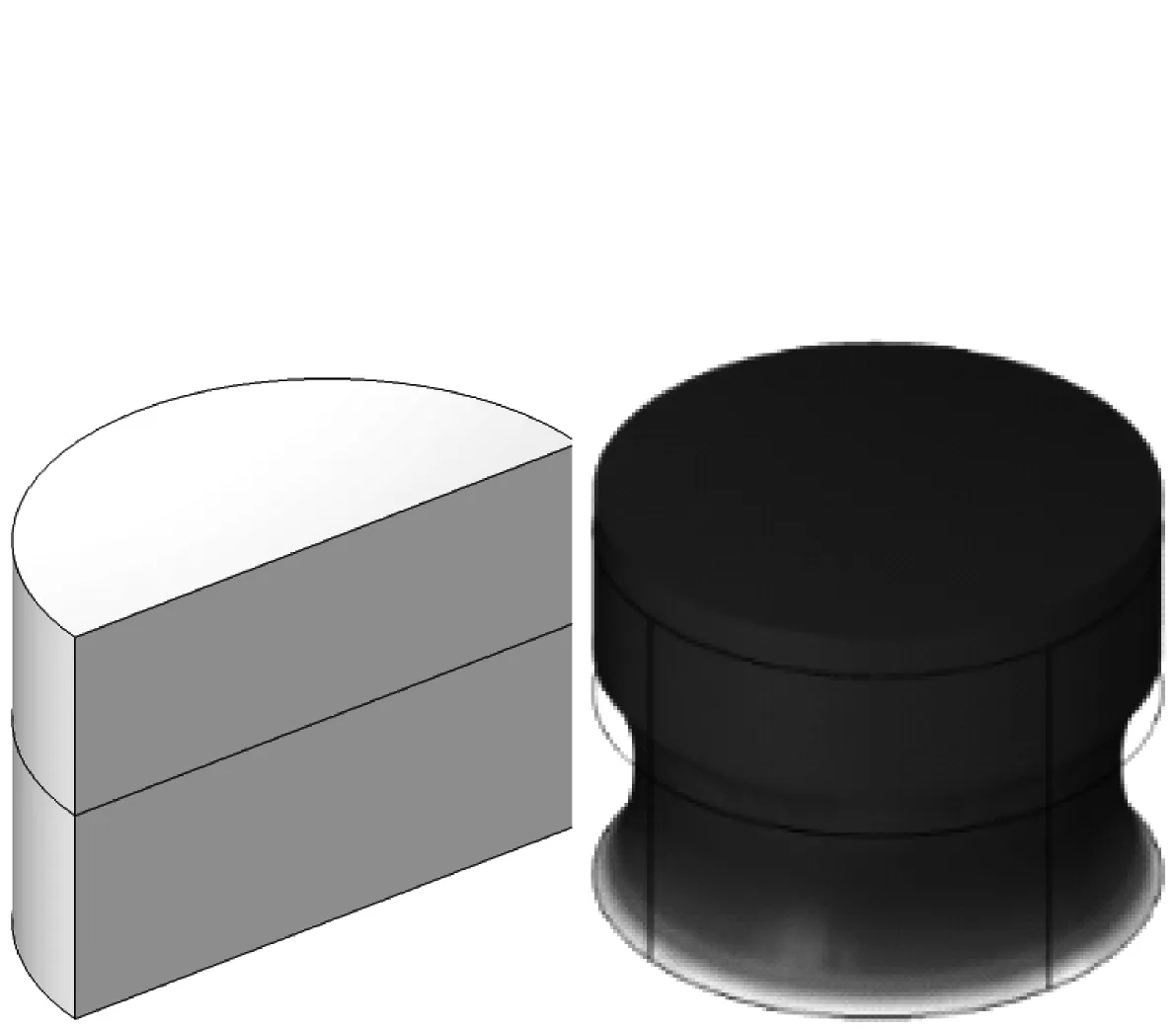
(a) 匀质质量块(f=144 Hz)

(27)

式中，h2,ρ2为与圆柱壳等质量匀质柱体质量块的高度和密度。

3 抑振器阵列振动控制效果

第2章对多模态低频抑振器初步设计模型进行了几何结构上的调整，利用理论公式分别计算各部分的等效刚度和等效质量。现在需要运用抑振器对平板振动响应曲线上的共振峰进行针对性抑制。

根据抑振器结构各部分等效参数的理论解以及吸振器参数，确定每个抑振器的几何参数和材料参数如下：橡胶基体半径r1=20 mm，高度h1=13.5 mm；金属柱壳厚度δ1=1 mm，其分为三部分，顶部部分用于固定顶部橡胶板的上表面边界，其厚度h2=δ1，中间部分用于固定顶部橡胶板的下表面边界和中间橡胶板的上表面边界，其高度h3=2.85 mm，支撑部分用于固定中间橡胶板的下表面边界，其高度h4=3.85 mm；中间橡胶板的厚度为δ2=1 mm，中间质量块半径为14.2 mm；顶部橡胶板的厚度为δ3=1.5 mm，顶部质量块半径为11.6 mm；质量块厚度与橡胶板厚度相同。橡胶基体杨氏模量为8.6×105Pa，中间橡胶板杨氏模量为2.31×106Pa，顶部橡胶板杨氏模量为9.97×106Pa，密度均为1 100 kg/m3，泊松比均为0.49，损耗因子η=0.1；金属柱壳杨氏模量为7×1010Pa，密度为2 700 kg/m3，泊松比为0.35；质量块杨氏模量为2×1011Pa，密度为7 850 kg/m3，泊松比为0.28。以上各材料参数如表1所示。

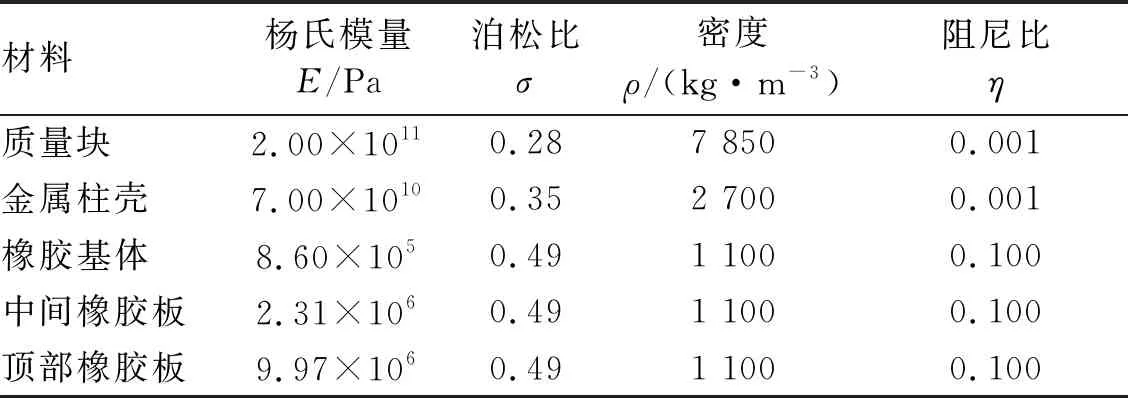
表1 抑振器各部分材料参数

将图11所示多模态低频抑振器模型阵列于平板上表面，如图12所示，单位简谐激励力作用于(0.08,0.08)位置处。平板附加抑振器阵列后的振动响应曲线如图13所示。

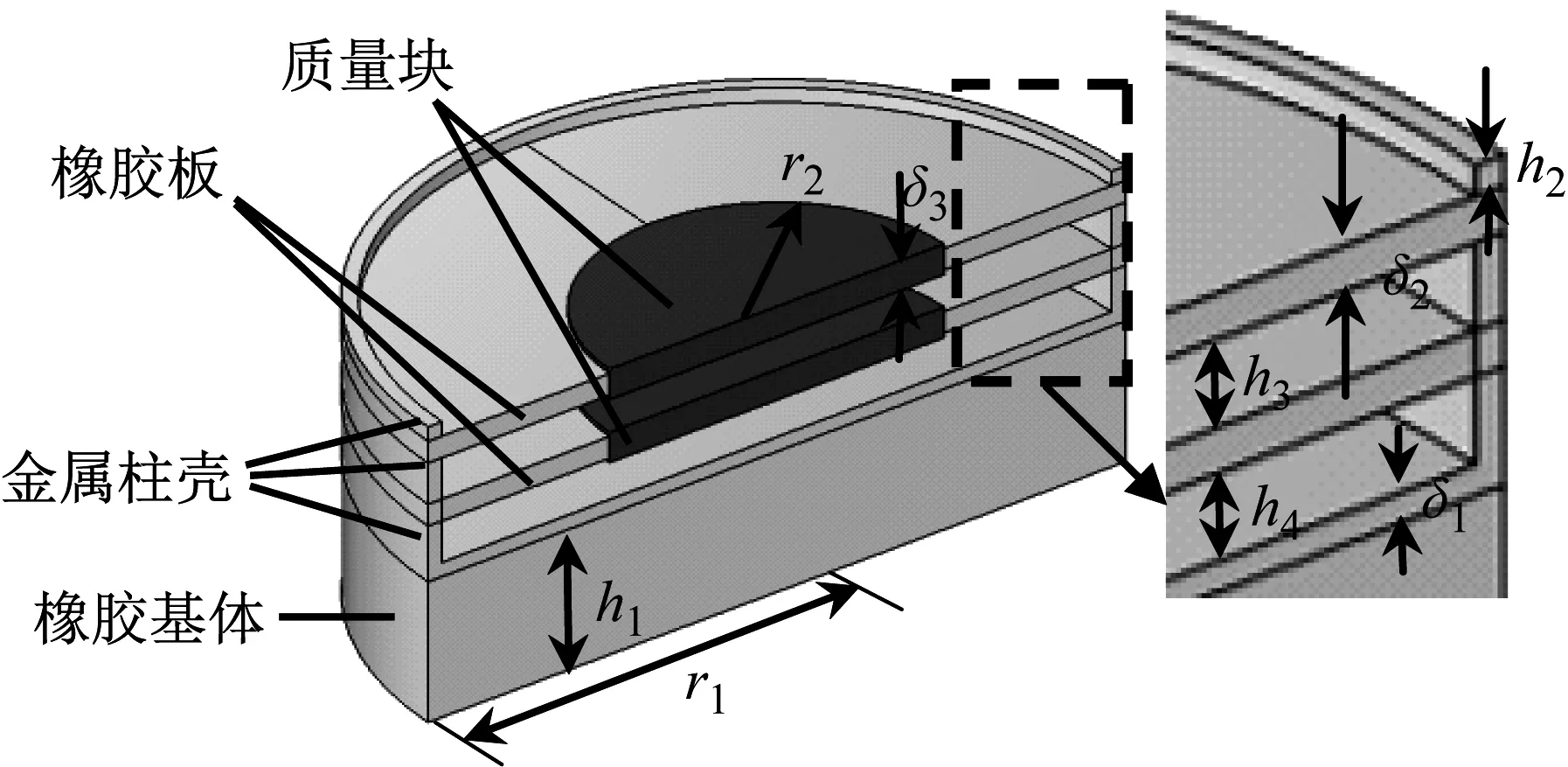
图11 多模态低频抑振器最终设计模型

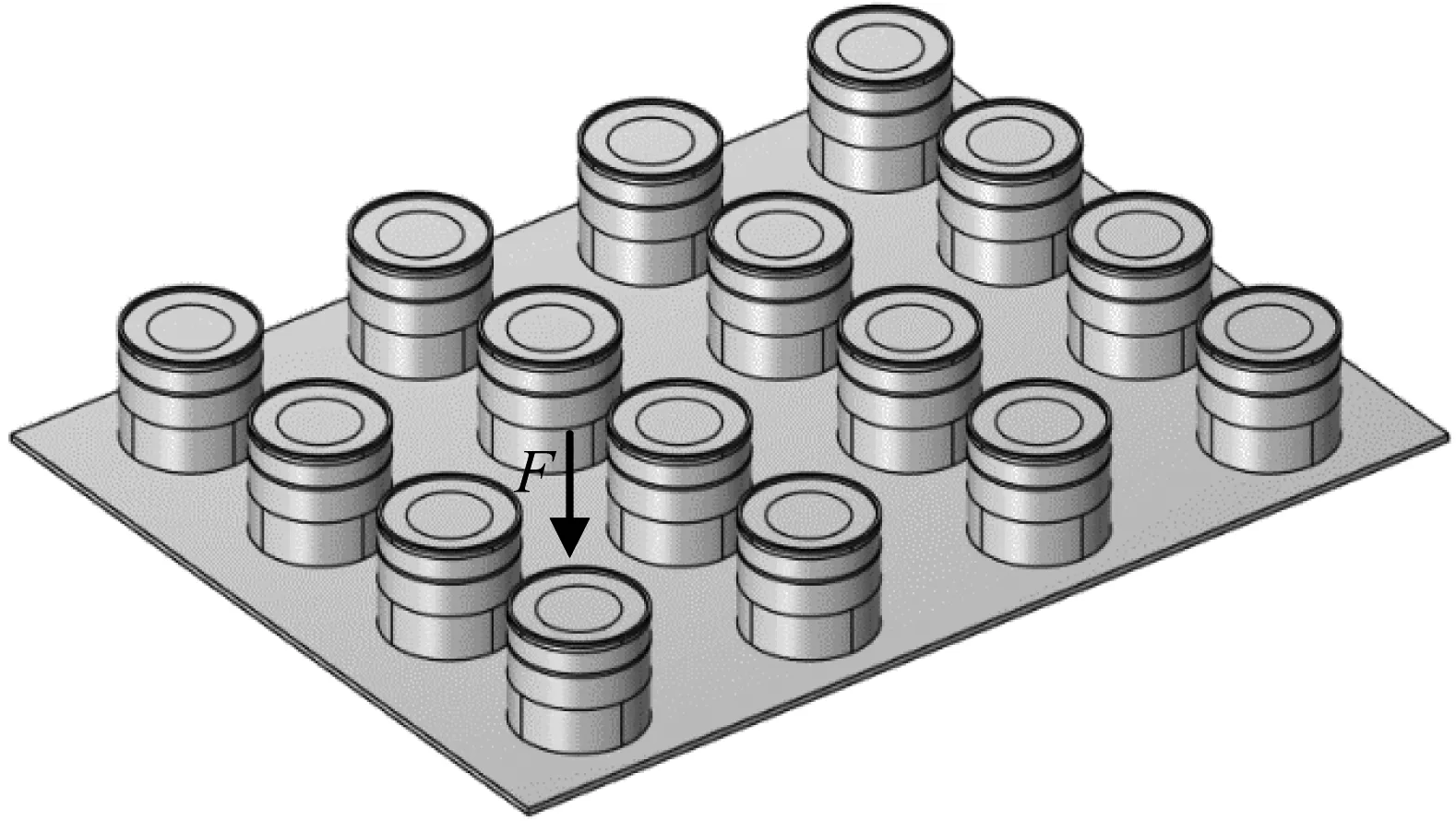
图12 多模态低频抑振器阵列

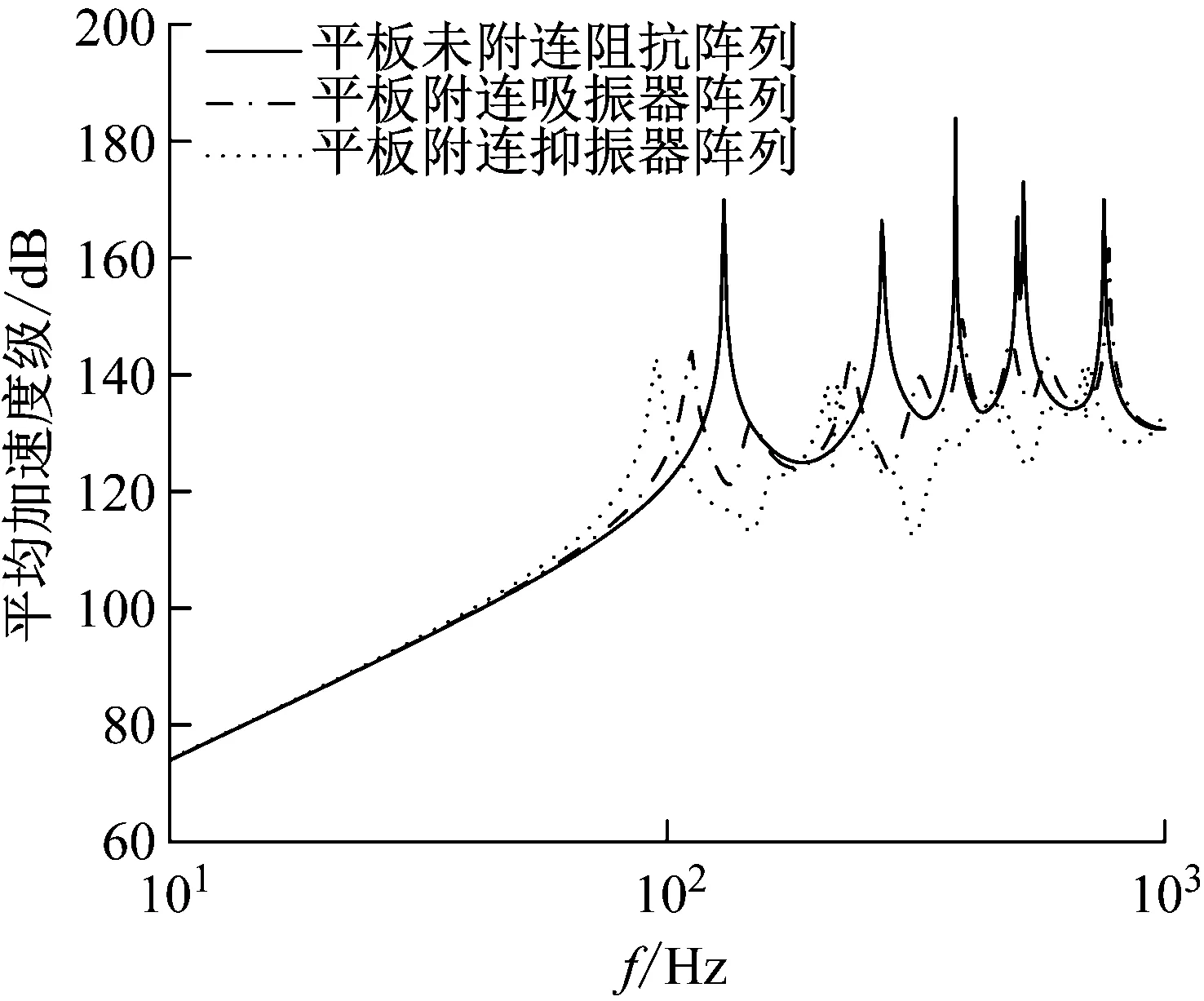
图13 平板附加阻抗阵列前后振动响应曲线

由图13可知，附加阻抗阵列后平板振动响应曲线的共振峰值均有明显下降，其中，附加抑振器阵列的振动控制效果更为明显，这是因为抑振器作为一个弹性体其模态之间存在干涉；而且同吸振器阵列与板之间为点接触不同，抑振器与板之间为面接触，阻尼效果更为显著，抑振频带也更宽。

4 抑振器阵列排布方式对抑振效果的影响

抑振器以3×3阵列于平板上的模型示意图，如图14所示;平板附加不同抑振器阵列后的振动响应频响曲线,如图15所示。

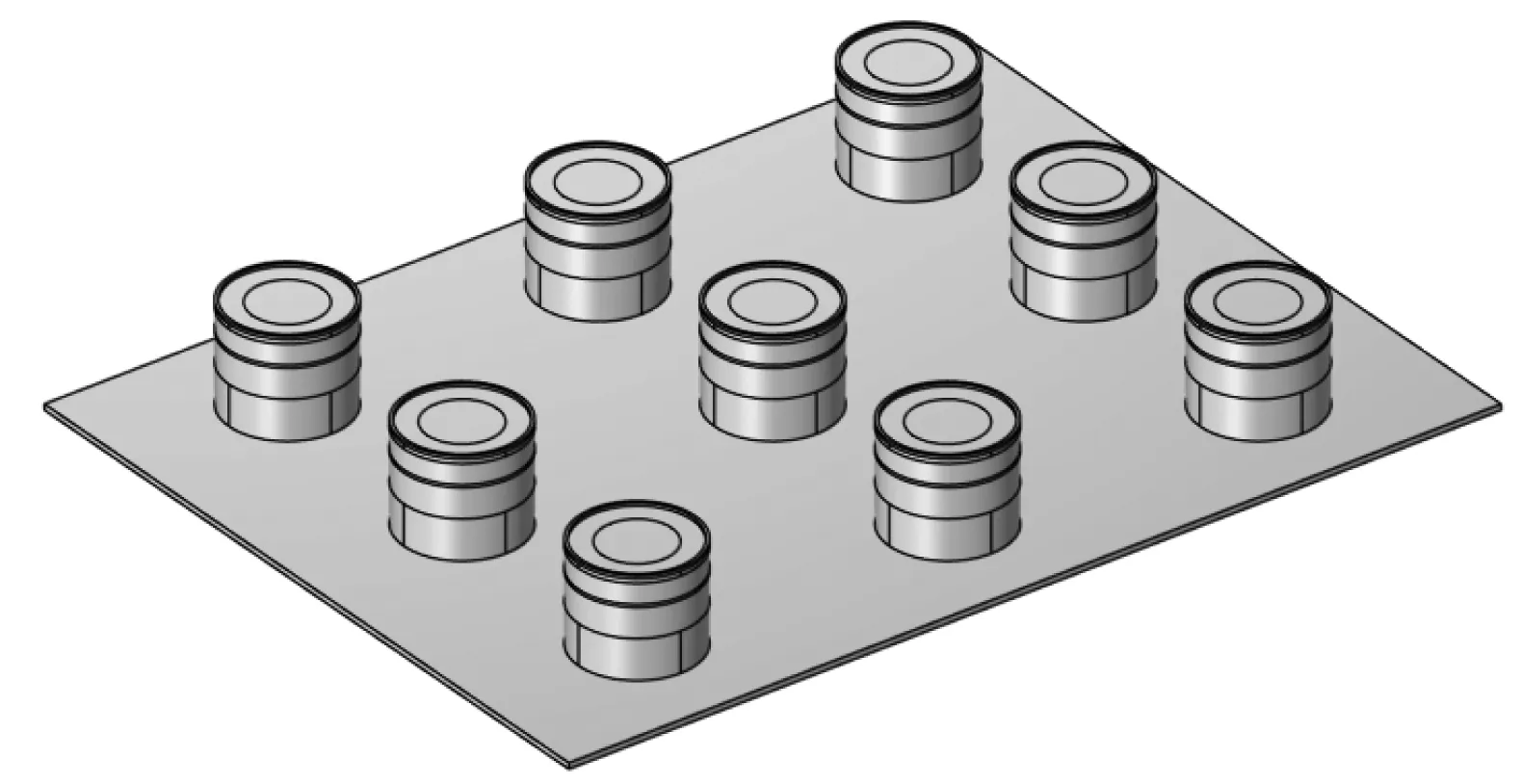
图14 抑振器3×3阵列示意图

图15 不同抑振器阵列排布方式对抑振效果的影响

由图15可知，两种阵列的振动控制效果基本相同，这是因为3×3阵列已基本覆盖平板主要模态的最大变形位置(见图16)，在此基础上继续增加抑振器会增大加工和安装成本，同时抑振效果并没有明显提升。进一步由图17中对应的吸振器阵列的振动控制效果可以看出， 3×3阵列和4×4阵列抑振效果基本一致，因此与4×4阵列相比，3×3阵列能够以较少的抑振器数量达到基本相同的抑振效果，大幅降低了安装成本，与4×4阵列相比，3×3阵列为更优的抑振器阵列排布方式。将以3×3阵列为基础开展实验研究。

(a) 第一阶模态(129 Hz)

图17 不同DVA阵列排布方式对抑振效果的影响

5 实验验证

5.1 实验模型、设备与工况

为验证所设计抑制器的抑振效果并与仿真结果进行对比，待抑振平板应与第2章中的待抑振平板尺寸保持一致，该待抑振平板长0.32 m、宽0.24 m、厚0.002 m，在平板表面附加所设计的抑制器阵列，阵列在x方向的布置间距为0.108 m，y方向的布置间距为0.08 m。为尽可能模拟四边简支边界条件，本实验还专门设计了夹具，夹具与平板之间通过圆棒上下加紧。抑制器结构尺寸及材料参数与第2章内容保持一致，考虑到所设计抑制器中各橡胶部件的杨氏模量不同，抑制器的橡胶基体均采用硅橡胶，橡胶环形板分别采用三元乙丙橡胶和氟橡胶，卧式抑制器的橡胶覆盖层采用硅橡胶。实验模型如图18所示。

(a) 平板

实验设备如图19所示。图19(a)为UTG9010C信号源，实验中用于产生频率范围10～1 000 Hz的扫频信号；图19(b)为MB500VI功放，实验中用于将信号放大后驱动激振器；图19(c)为MB Dynamics模态激振器，实验中用于产生点激励力；图19(d)为INV3062V采集分析仪，实验中用于采集信号数据。

(a) UTG9010C信号源

实验中，信号源(UTG9010C)发出的信号经过功率放大器(MB500VI)后驱动激振器(MB500VI)，激振器与试件之间通过力传感器连接，用于采集受激点激励力，加速度传感器采集到的信号经激励点力信号归一化后即可得到各测点导纳数据。

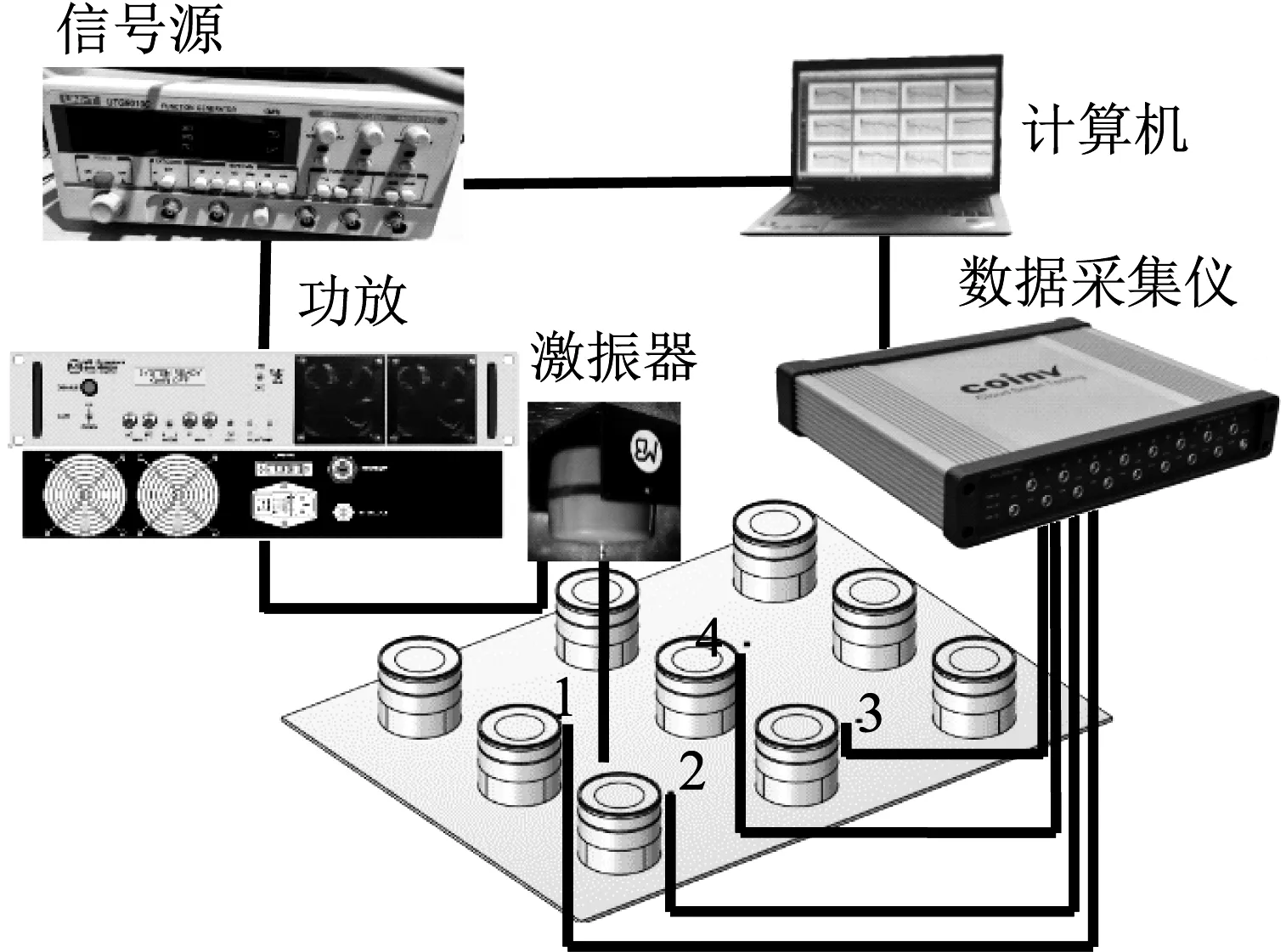
图20 实验系统示意图

5.2 测试原理

本实验的主要抑振性能指标为机械导纳，其定义为机械阻抗的倒数，即单位稳态力激励下的振动响应。通常实验中无法保证激励始终为单位激励，因此引入机械导纳这一概念实现振动响应的归一化，有助于与仿真结果进行对比分析。根据测试点位置，机械导纳可分为输入导纳和传递导纳，输入导纳定义为激励点位置处振动响应与激励力幅值的比值，传递导纳定义为非激励点位置处振动响应与激励力幅值的比值；根据所取振动响应的不同，机械导纳还可分为加速度导纳、速度导纳以及位移导纳。本实验中的机械导纳为加速度传递导纳，其表达式为

(28)

平均加速度导纳级可由式(21)得到

(29)

式中，i为测点序号。

5.3 实验结果

对四边简支板进行线性扫频激励，提取各测点振动响应，并利用力信号归一化处理后得到单位力激励下各测点振动响应，平板振动响应曲线和平板附连不同抑制器阵列后的振动响应曲线如图21、图22所示。

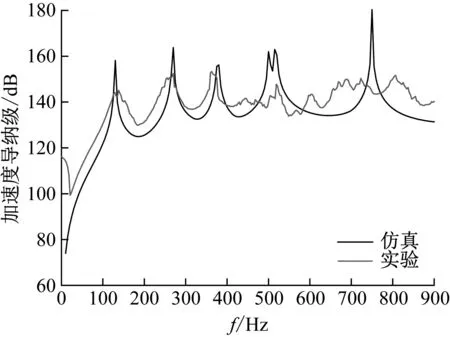
图21 平板振动响应曲线(实验与仿真结果对比)

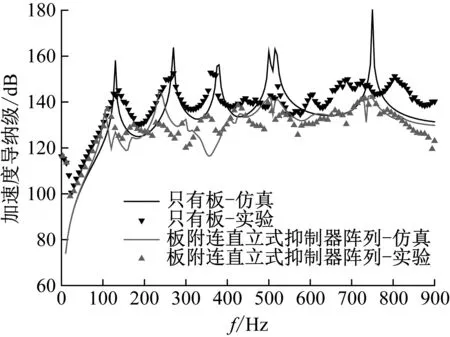
图22 抑制器振动控制效果对比曲线

由图21可知，平板振动响应曲线的仿真和实验结果基本一致，由此可以基本判定本实验所设计的夹具能够保证平板处于四边简支边界条件。由图22可知，实验测试得到的平板附连不同抑制器阵列后的加速度导纳级振动响应曲线与仿真结果也基本吻合，且与仿真结果相比，实验结果在大多数频段下的振动响应更低，这是由于仿真中的结构阻尼与实际结构的结构阻尼并不完全相同，实际结构与平板之间通过胶粘的方式相固定也会进一步增大阻尼在振动控制中的影响。在附连抑制器阵列后，平板的在选定共振频率处的峰值响应大幅下降，实验频段内振动响应平均降低9.63 dB，由此可以验证抑制器阵列对平板的振动控制效果。

6 结 论

本文首先研究了平板振动特性，确定了通过附加吸振器阵列抑制其低频共振峰的振动控制策略，通过合理选取动力吸振器参数，一定程度上降低了平板部分低频共振峰值；进而提出了一种具有多模态特性的低频抑振器，从理论上计算了其各部分的等效刚度与等效质量，并以吸振器参数为基准对抑振器各组成部分的材料参数和几何参数进行调整，最终通过实验验证了多模态低频抑振器阵列的控制效果。分析得出结论如下：

(1) 吸振器阵列和以吸振器参数为基准设计的抑振器阵列对选定共振峰均有一定控制效果，其中抑振器阵列的振动控制效果更为明显。这是因为吸振器理论模型实体化后结构与抑振对象之间由点接触变为面基础，一定程度上放大了阻尼在振动控制中的作用。

(2) 为达到多模态抑振效果，橡胶基体-金属柱壳部分的轴向共振模态频率要与选定最高阶共振峰对应频率相同，以避免发生隔振，振动无法传递到其余部件。

(3) 所设计抑振器阵列对共振峰有明显控制效果的同时，在其两侧产生了新的共振峰，因此需进一步优化结构，在不引入新共振峰的条件下降低原有共振峰的振动响应。

(4) 通过研究抑振器阵列排布方式对抑振性能的影响，得出当以最少抑振器数量覆盖结构所有主要模态下的最大变形位置时，即可达到与密集阵列相同的抑振效果，加工和安装成本也更低。

(5) 为更好地模拟四边简支边界条件，还专门设计制作了夹具和用于固定夹具的工字钢、T型梁，并开展了实验验证工作。实验对比分析了附连抑制器阵列前后四边简支板的振动响应，并与仿真结果进行了对比，实验结果显示，实验频段内振动响应平均降低9.63 dB，由此可以验证抑制器阵列对平板的振动控制效果。