考虑物理加载时滞的力修正迭代混合试验方法

王 涛， 浩杰敦， 孟丽岩， 郑 欢， 龚越峰， 王 贞， 许国山

(1.黑龙江科技大学 建筑工程学院，哈尔滨 150022；2.武汉理工大学 土木与建筑学院，武汉 430070；3.哈尔滨工业大学 土木工程学院，哈尔滨 150090)

实时混合试验(real-time hybrid test,RHT)[1]采用物理试验和数值模拟实时数据交互的方式评估结构动力性能。该方法要求在每个时间步内完成运动方程求解、加载命令传递、动力加载、数据反馈等一系列流程。动力加载与数据反馈不同步将导致试验结果发散。

作动器从接收命令到实现命令所需要的时间为加载时滞[2]。针对加载时滞问题，学者们提出了系列时滞补偿方法[3-6]。数值结构从接收试验结构反馈信号到计算出下一积分步的时间为计算时滞[7]。针对计算时滞问题，学者们提出了基于重启动的实时混合试验方法(restarting based real-time hybrid testing method, R-RHT)[8-9]与迭代混合试验(iterative hybrid test,IHT)方法[10-11]。R-RHT方法基本原理是，当计算时滞大于积分步，作动器会停止加载并回到初始位置，等待数值计算到当前步的加载命令，作动器再进行连续加载直至当前步，再进行下一步的数值计算与物理加载。IHT方法将传统RHT以积分步实时交互方式转变成全时程离线交互方式，通过全时程迭代获取结构真实响应，避开了计算时滞问题。IHT方法被广泛应用于汽车轮胎耐久性测试[12]、非结构构件抗震性能评估[13]、偏置电力变压器性能评估[14]、车桥耦合振动性能评估[15-16]等多个领域。然而，IHT方法在求解下一轮次全时程结构响应时，试验子结构(experimental substructure,ES)实测反力值与运动方程积分算法求解存在轮次差的问题，导致运动方程求解精度和迭代收敛效率降低。针对这一问题，王涛等[17-19]于2021年在IHT方法基础上提出了力修正迭代混合试验方法(force correction iterative hybrid test, FCIHT)，该方法基于等效ES数值模型和相邻两迭代轮次的速度、位移响应修正每一迭代轮次ES反力，从而减小轮次差的影响。FCIHT方法解决了RHT的计算时滞问题，尚未考虑物理加载时滞带来的不利影响，需进一步研究物理加载时滞对FCIHT方法精度和迭代收敛效率的影响规律。

本文在FCIHT方法基础上考虑物理加载时滞影响，提出PLTD-FCIHT(force correction iterative hybrid test method considering physical loading time delay)方法，给出方法原理及流程，以三层框架-黏滞阻尼器减震结构为研究对象，对所提方法进行数值验证，分析加载时滞大小对所提方法收敛性的影响规律。

1 PLTD-FCIHT方法原理及流程

PLTD-FCIHT方法包括全时程内数值计算与物理加载的内环控制和全时程轮次间迭代收敛外环控制。在内环控制中进行物理加载时滞补偿和力修正运动方程数值积分，在外环控制中采用不动点迭代[20]，构成双环控制框架，以提高试验精度与迭代收敛效率。PLTD-FCIHT方法原理如图1所示。

1.1 PLTD-FCIHT方法时程内环

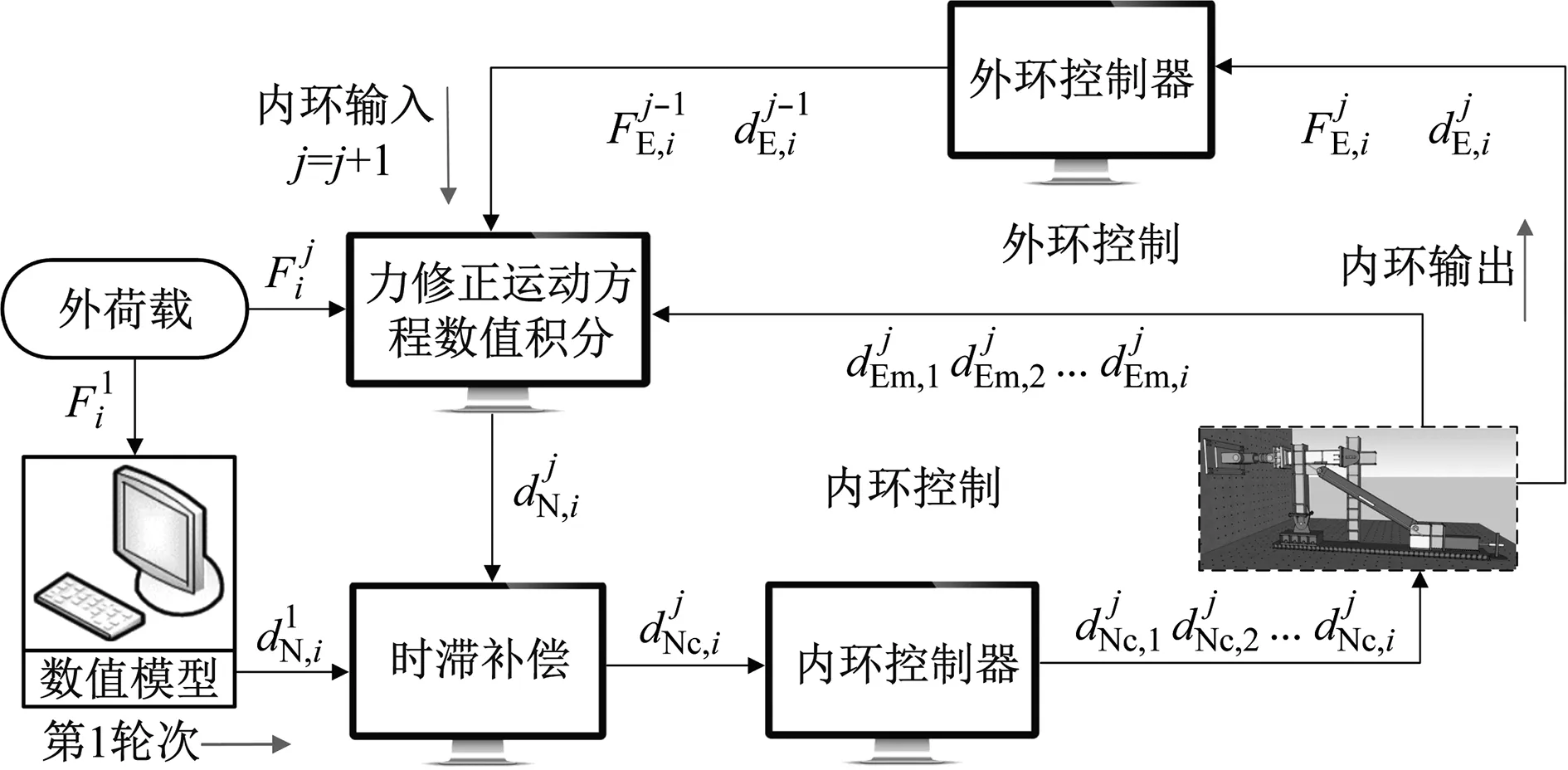
图1 PLTD-FCIHT方法原理图

(1)

(2)

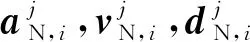
值得说明的是在迭代第j轮次，NS与ES的实时数值计算、时滞补偿、物理加载、反力修正，形成一个时程内的闭环，时滞补偿与力修正策略能在一定程度上保证试验加载精度与运动方程求解精度。本文将通过数值模拟验证考虑物理加载时滞下力修正策略的有效性，同时进一步分析加载时滞大小对迭代收敛性的影响。

1.2 PLTD-FCIHT方法时程外环

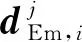
值得说明的是在迭代第j轮次，NS计算、ES加载与两者之间的时程数据交互，形成一个时程间的闭环，通过不动点迭代算法，逐步减小迭代第j-1轮次与第j轮次的位移响应误差，直至满足收敛目标要求，则第j轮次的结构响应为结构最终的试验结果。

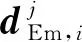
(3)

(4)

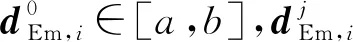
(5)

则称为不动点迭代法收敛，d*为式(4)的解。

PLTD-FCIHT方法流程如图2所示，图2中n为一个时程总的积分步数。

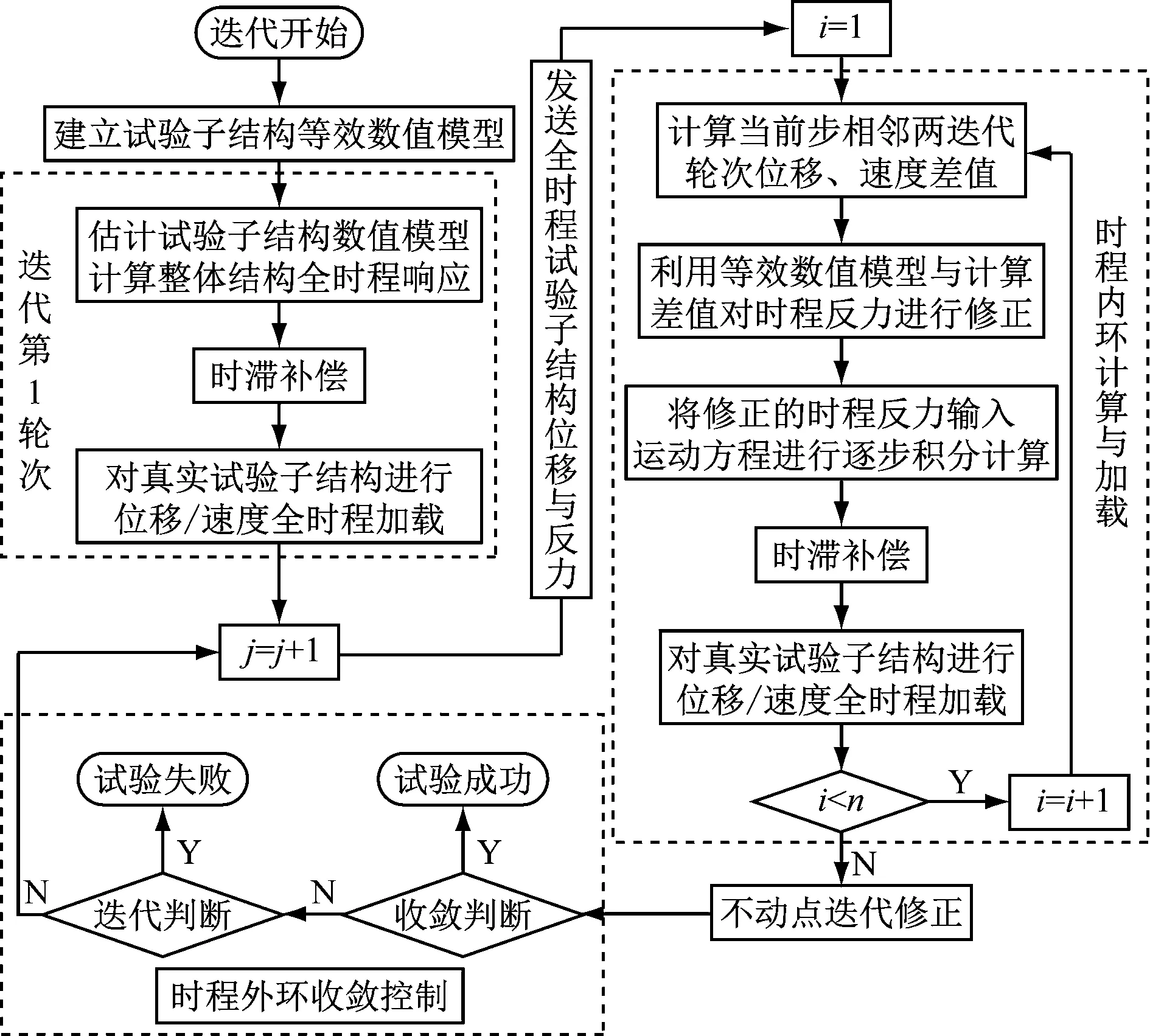
图2 PLTD-FCIHT方法流程图

假定ES是弹簧-阻尼的线性系统，那么在迭代第1轮次参与运动方程逐步求解时的ES反力为

(6)

式中,ac,ak分别为假定的ES阻尼系数和刚度系数。

在实际工程中，假定的ES阻尼和刚度不可避免的会带来初始估计误差，通常ac≠1和ak≠1。

2 PLTD-FCIHT方法实施方案设计

2.1 实施工况设计

为验证PLTD-FCIHT方法有效性，以三层框架-黏滞阻尼器减震结构为例进行计算。以首层的黏滞阻尼器作为ES，其余部位作为NS，将两者结合进行数值模拟。

三层框架结构各层质量均为2×104kg，各层抗侧刚度均为4×107N/m，结构阻尼采用瑞利阻尼，阻尼系数矩阵由质量矩阵和刚度矩阵线性组合计算，即C=a1M+a2K。瑞利阻尼的比例系数a1与a2由结构阻尼比与频率确定。该结构前2阶振型阻尼比ζ0均为2%，前3阶频率分别为3.17 Hz,8.88 Hz和12.8 Hz。NS质量M，阻尼C和刚度K分别为

(7)

(8)

(9)

地震激励为El Centro (NS，1940) 地震加速度记录，峰值加速度调整为70 gal，积分步长为1/1 024 s，每一轮次的积分步数为10 240步。

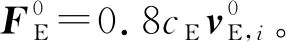
在迭代第j轮次，黏滞阻尼器的力学模型为

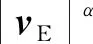
(10)

式中:FE为阻尼力向量;cE为阻尼系数;α为速度指数。

速度指数α=0.35，阻尼器系数cE=4.14×105(N·s)/m。为避免试验加载过程中位移响应发散，设置位移限值20 mm。为模拟控制器、作动器、黏滞阻尼器组成的试验伺服加载系统，本文选用文献[21]提出的传递函数作为加载系统模型，文献[22]利用高阶加载系统模型对该二阶简化模型进行了验证，结果表明该二阶简化模型的精度较高，可以替代实际的试验伺服加载系统开展数值仿真工作。该二阶传递函数表达如下

(11)

式中:ωE与ζE分别为该系统的圆频率与阻尼比;τ1为系统纯时滞;s为拉普拉斯算子。本文选用ωE=45,ζE=0.78，同时由于τ1远小于加载时滞，故忽略τ1的影响。为考虑真实试验测量噪声与AD,DA转换噪声，分别对试验伺服加载系统位移的输入和输出加入标准差约0.01 mm的白噪声。

时滞补偿采用三阶多项式外插方法，如式(12)，时滞大小τ通过求取前期离线试验数据的最小值确定，如式(13)。

(12)

(13)

式中：Δt为积分步长；b为数据点的数目；ti为计算第i步的时间。

以第j轮次试验为例，三层框架-黏滞阻尼器减震结构PLTD-FCIHT方法示意图,如图3所示。

图3 PLTD-FCIHT方法示意图

具体试验操作流程如下。

(1) 建立模型阶段：①对三层框架结构进行划分,将黏滞阻尼器作为ES，结构其余部位作为NS，并建立两者动力学边界关系；②开展前期试验，利用历史数据建立等效黏滞阻尼器数值模型。

(2) 试验第1轮次：①假定黏滞阻尼器数值模型，设定数值结构参数，输入外部激励，对整体结构进行数值模拟，获得全时程响应；②对第1轮次的时程位移进行补偿，获取补偿后的时程命令位移，然后在伺服加载系统中对黏滞阻尼器进行实时加载，测得黏滞阻尼器第1轮次的时程反力与时程位移；③通过外环收敛控制器将全时程反力与位移传递至第2迭代轮次。

(3) 试验第j(j≥2)轮次：①将试验j-1轮次的黏滞阻尼器时程反力输入运动方程，同时基于黏滞阻尼器数值模型与相邻两迭代轮次的位移、速度响应差值对第j-1轮次传递的时程反力进行修正，逐步求解第j轮次的全时程响应；②对第j轮次的时程位移进行时滞补偿，通过补偿的命令位移，在伺服加载系统中对黏滞阻尼器进行实时加载，实时逐步反馈实测位移数据到运动方程数值积分模块开展力修正数值计算，同时保存黏滞阻尼器第j轮次的时程反力与时程位移；③在时程轮次间逐步传递全时程反力与位移实测向量，开展时程外环不动点迭代收敛判断。

(4) 试验控制阶段：①进行收敛判断，若收敛即试验成功，否则进行轮次判断；②对于已经进行j轮的试验次数与限定jmax轮的试验次数进行对比，若未达到jmax，则继续迭代加载，若达到jmax，则结束试验。

2.2 收敛评价指标设计

为了对所要开展的模拟工况进行分析与评价，进行纯数值模拟计算得到理想状态下结构时程位移响应的参考解di。

为了定量分析每一轮次下迭代收敛的快慢，定义收敛速度的评价指标如式(14)所示。该指标表示结构模拟工况在相邻两迭代轮次的第i积分步前的输入时程位移差值小于收敛速度误差限值R，即认为该工况在第j轮次收敛δj步。当该模拟工况的收敛步数为10 240步时，即认为迭代完全收敛。其中误差限值R根据工程精度要求设定，通常取小于参考解幅值的2%。

(14)

为了定量评估迭代收敛过程，定义局部峰值误差e1与相对面积误差e2评价指标如式(15)和式(16)所示。式(15)表示结构相邻两迭代轮次在第i积分步下输入时程位移差值绝对值的最大值，该指标能够体现PLTD-FCIHT的收敛精度；式(16)表示结构相邻两迭代轮次在第i积分步下输入时程位移差值，与上一迭代轮次输入时程位移的相对面积比值，该指标能够体现PLTD-FCIHT整体稳定程度。

(15)

(16)

3 数值验证

为检验PLTD-FCIHT方法的有效性，本文在数值环境下分别对力修正策略与不动点迭代策略展开验证。分别设计力修正系数γ为0.8,0.4与0的模拟工况。工况1即γ=0.8与工况2即γ=0.4表示开展不同力修正系数的PLTD-FCIHT，工况3即γ=0表示开展传统的IHT。

为验证不动点迭代策略，图4展示了不同迭代轮次下3种工况的首层位移响应与参考解的对比。由图4可见，随着迭代轮次的增加，3种模拟工况与参考解的时程位移响应吻合程度在不断增加；工况1在第5轮迭代时，与参考解的时程位移基本吻合；工况2在第15轮迭代时，与参考解时程位移偏差较大；工况3在第15轮迭代时，与参考解时程位移偏差最大。这表明不动点迭代策略能复现结构响应，但所需试验轮次较多。

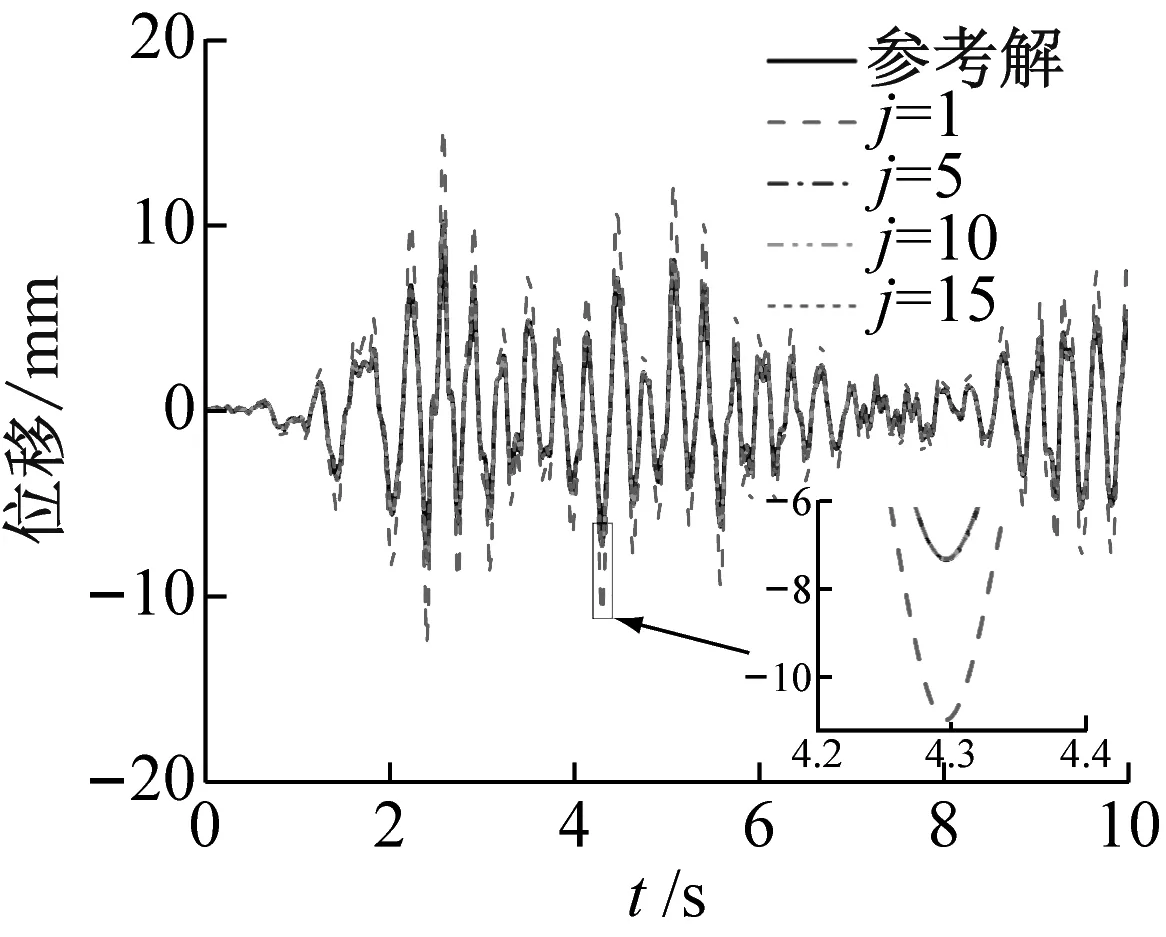
(a) 工况1

为验证力修正策略，图5展示了3种工况在迭代第1～第5轮的首层位移响应与参考解的对比。由图5可见，在迭代第1轮，3种工况下的位移响应与参考解都有较大的偏差；在迭代第2～第5轮，随着力修正系数的增加，结构位移响应与参考解的吻合程度逐渐增加。在迭代第5轮，当γ=0.8的位移响应与参考解已基本吻合，γ=0.4次之，当γ=0时的偏差最大。这表明力修正策略能有效减少迭代轮次的需求，同时力修正所采用的模型越精确，所需试验迭代轮次就越少，试验耗时就越短。

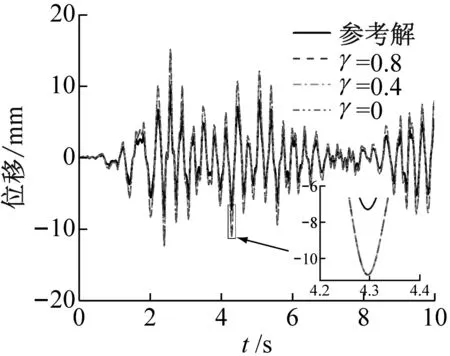
(a) 第一轮

为定量评价PLTD-FCIHT的收敛性，采用迭代收敛评价指标，计算出3种工况下每一轮次结构响应的收敛步数、局部峰值误差e1、相对面积误差e2，结果如图6、图7所示。在本算例中，当该模拟工况在第j轮次下的e1<0.2 mm，e2<2%时，即认为迭代收敛，可满足工程精度要求。

其中式(14)中收敛步数误差限值R=0.3 mm，得到不同力修正系数下迭代收敛步数,如图6所示。由图6可见，在迭代第1轮后，随着力修正系数的增加，迭代收敛步数逐渐增加，同时当γ=0.8时，迭代收敛步数的增加较为迅速，在迭代第3轮结束时，迭代收敛步数为10 240步，即迭代完全收敛。在迭代前5轮次，当γ=0.4，γ=0处于迭代不完全收敛状态，同时γ=0.4迭代收敛步数增加极为缓慢。这表明力修正策略能较为有效的提高迭代收敛速度，同时力修正所采用的模型越精确，迭代收敛速度越快。

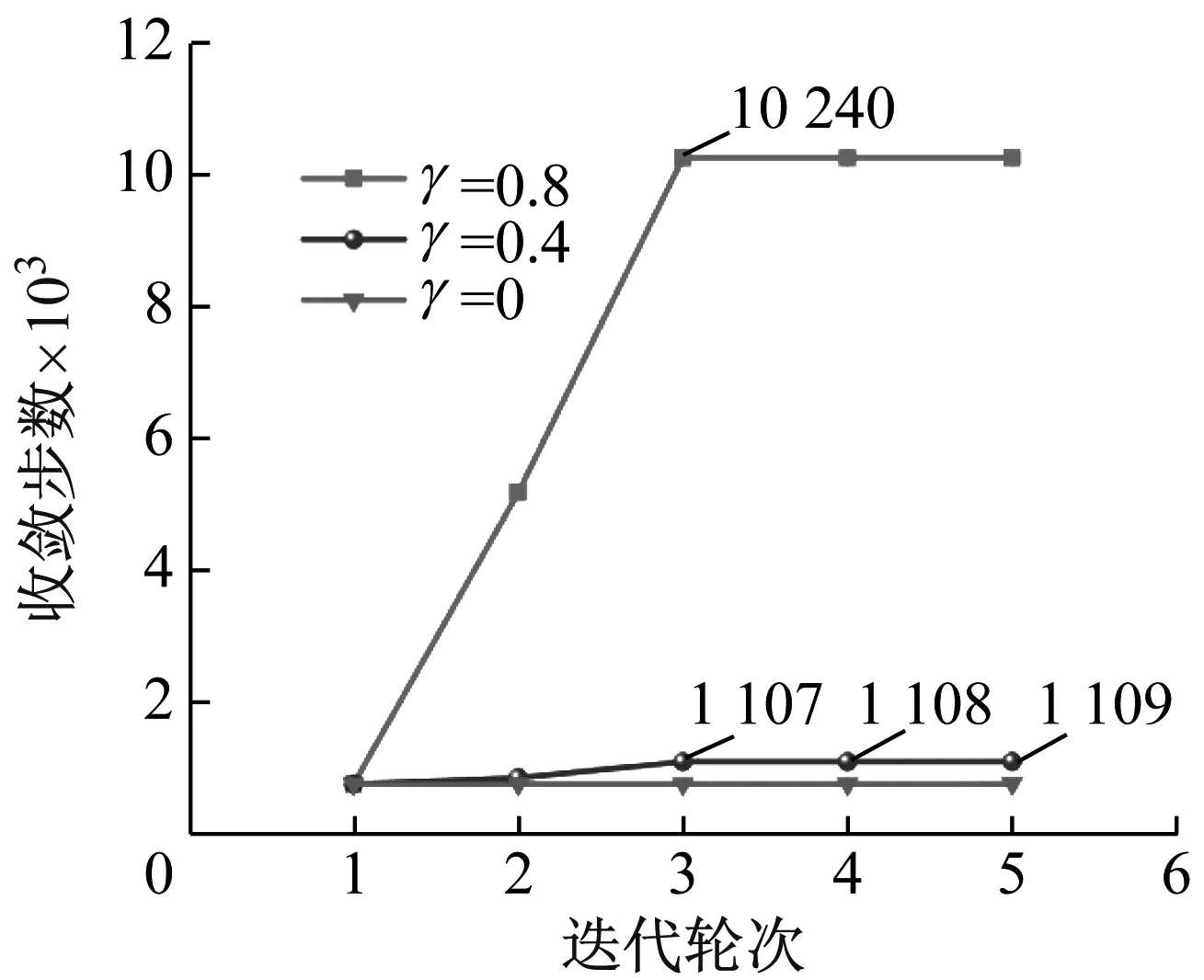
图6 不同力修正系数下迭代收敛步数

不同力修正系数下迭代误差,如图7所示。由图7可见，在迭代第1轮结束时，3种工况的e1与e2均为最大，分别为4.13 mm和50.65%。当γ=0.8，在迭代第3轮结束时，e1已降低至0.2 mm，在迭代第4轮结束时，e2已降低至2.00%。当γ=0.4与γ=0时，在迭代5轮内，e1与e2不满足迭代收敛目标。相较于γ=0时，γ=0.4的e1与e2更小。这表明力修正策略能较为有效的降低迭代收敛误差，同时力修正所采用的模型越精确，迭代收敛精度越高。

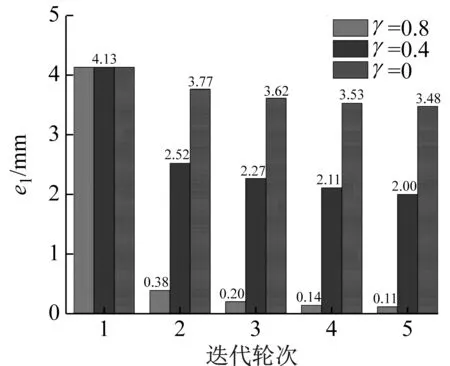
(a) 局部峰值误差

根据试验结果可知，随着迭代轮次的增加，IHT最终都能得到一个收敛解，但是试验耗时较大。力修正策略能有效提高迭代收敛效率，缩短试验耗时。

4 时滞影响分析

为进一步分析物理加载时滞对PLTD-FCIHT的影响，本文设计定时滞大小分别为15 ms,30 ms,45 ms的模拟工况，如表1所示。

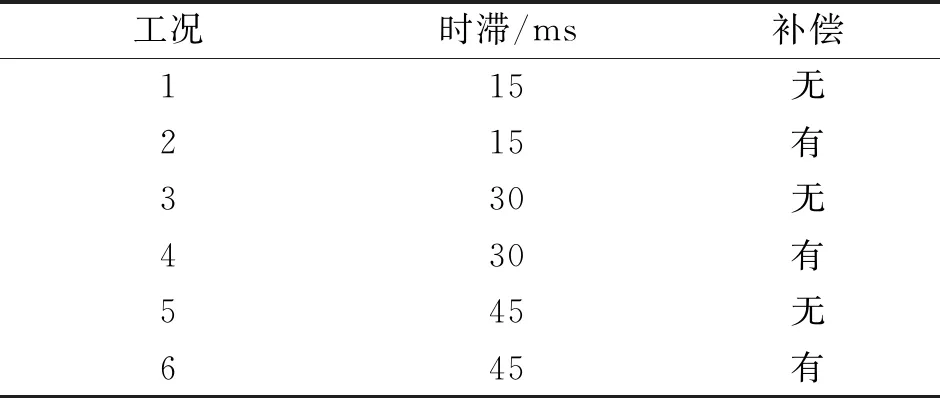
表1 模拟工况

采用迭代收敛评价指标，探究加载时滞大小对PLTD-FCIHT迭代收敛性的影响。为更明显得到加载时滞对PLTD-FCIHT迭代收敛性的影响规律，调整式(6)假定黏滞阻尼器的阻尼系数ac为0.5，刚度系数ak为0，力修正系数γ为0.8，同时为考虑补偿精度对PLTD-FCIHT迭代收敛性的影响规律，对式(12)中采样步长一致取10，即Δt=10/1 024 s。

其中式(14)中收敛步数误差限值R=0.3 mm，得到不同工况下迭代收敛步数如图8所示。由图8可见，随着迭代轮次的增加，不同工况下的收敛步数逐渐增加。在迭代5轮次内，与无位移补偿策略(工况1、工况3、工况5)相比，有位移补偿策略(工况2、工况4、工况6)在相同时滞大小与迭代轮次下的迭代收敛步数增加更快，同时无位移补偿策略均处于不完全收敛状态，有位移补偿策略均收敛10 240步，即迭代完全收敛，这表明位移补偿策略能有效提高迭代收敛速度。当无位移补偿策略时，在相同迭代轮次下，工况1时滞为15 ms，其收敛步数增加最快；工况3时滞为30 ms，其收敛步数增加次之；工况5时滞为45 ms，其收敛步数增加最慢。当有位移补偿策略时，在相同迭代轮次下，工况2时滞为15 ms，其收敛步数增加最快；工况4时滞为30 ms，其收敛步数增加次之；工况6时滞为45 ms，其收敛步数增加最慢。这表明随着物理加载时滞的增大，迭代收敛速度逐渐变慢。

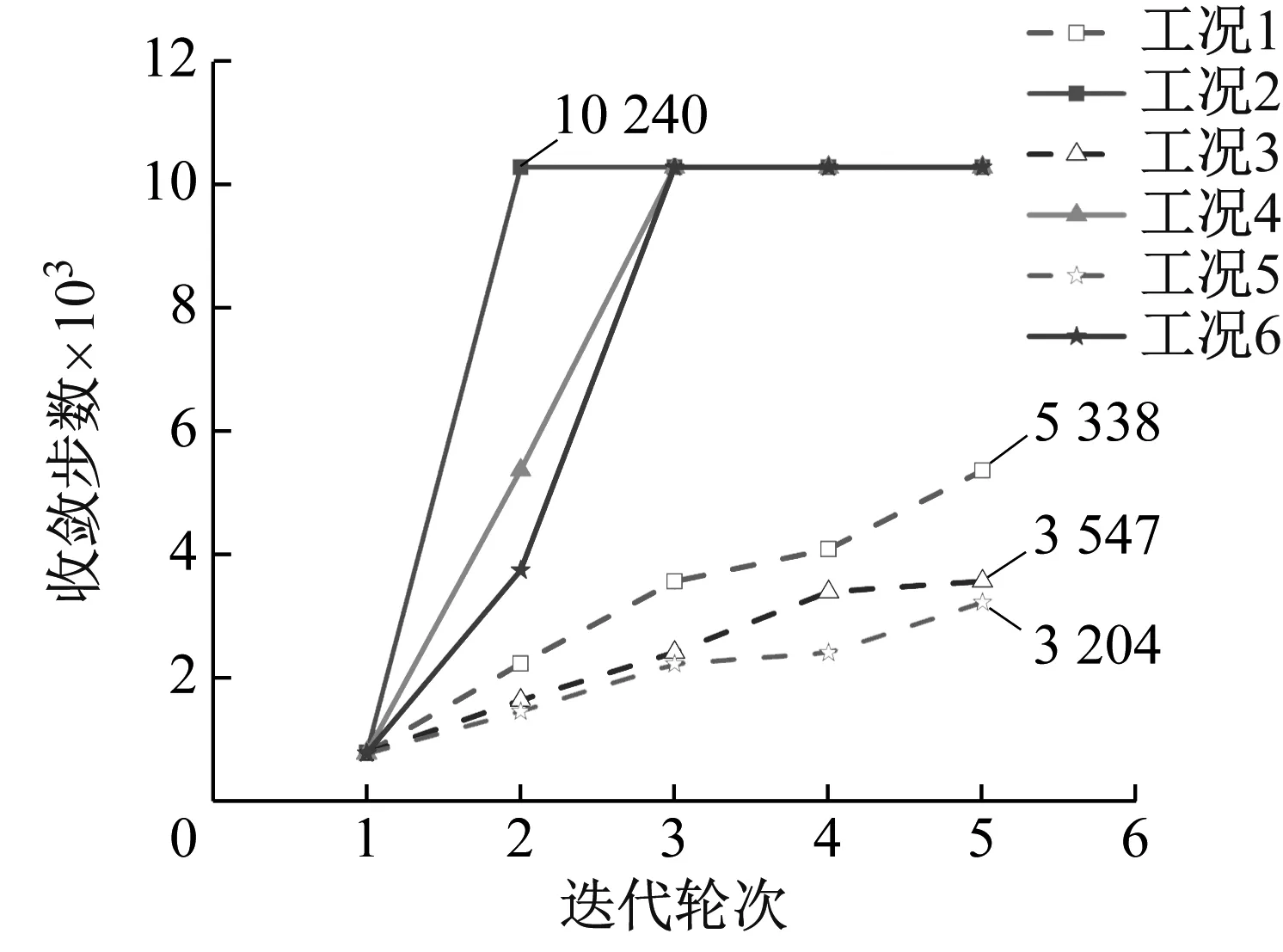
图8 物理加载时滞对迭代收敛步数的影响

不同工况下迭代误差结果,如图9所示。由图9可见，随着迭代轮次的增加，不同工况下的e1与e2逐渐减小。在迭代5轮次内，与无位移补偿策略(工况1、工况3、工况5)相比，有位移补偿策略(工况2、工况4、工况6)在相同时滞大小与迭代轮次下的e1与e2更小。在迭代第5轮次结束时，有无位移补偿策略的e1与e2相差最小，此时对比工况1，工况2的e1与e2分别减小了39.09%与29.99%；对比工况3，工况4的e1与e2分别减小了63.16%与58.27%；对比工况5，工况6的e1与e2分别减小了58.87%与65.53%。这表明在相同时滞大小下，位移补偿策略均能有效降低迭代收敛误差，提高迭代收敛精度。当无位移补偿策略时，不同轮次下物理加载时滞越小迭代的e1与e2越小；当有位移补偿策略时，受限于试验伺服加载系统非线性以及时滞补偿精度等因素的影响，时滞大小对迭代的e1,e2影响规律在迭代2轮后并不明显，这表明位移预测补偿精度也会影响迭代收敛精度。

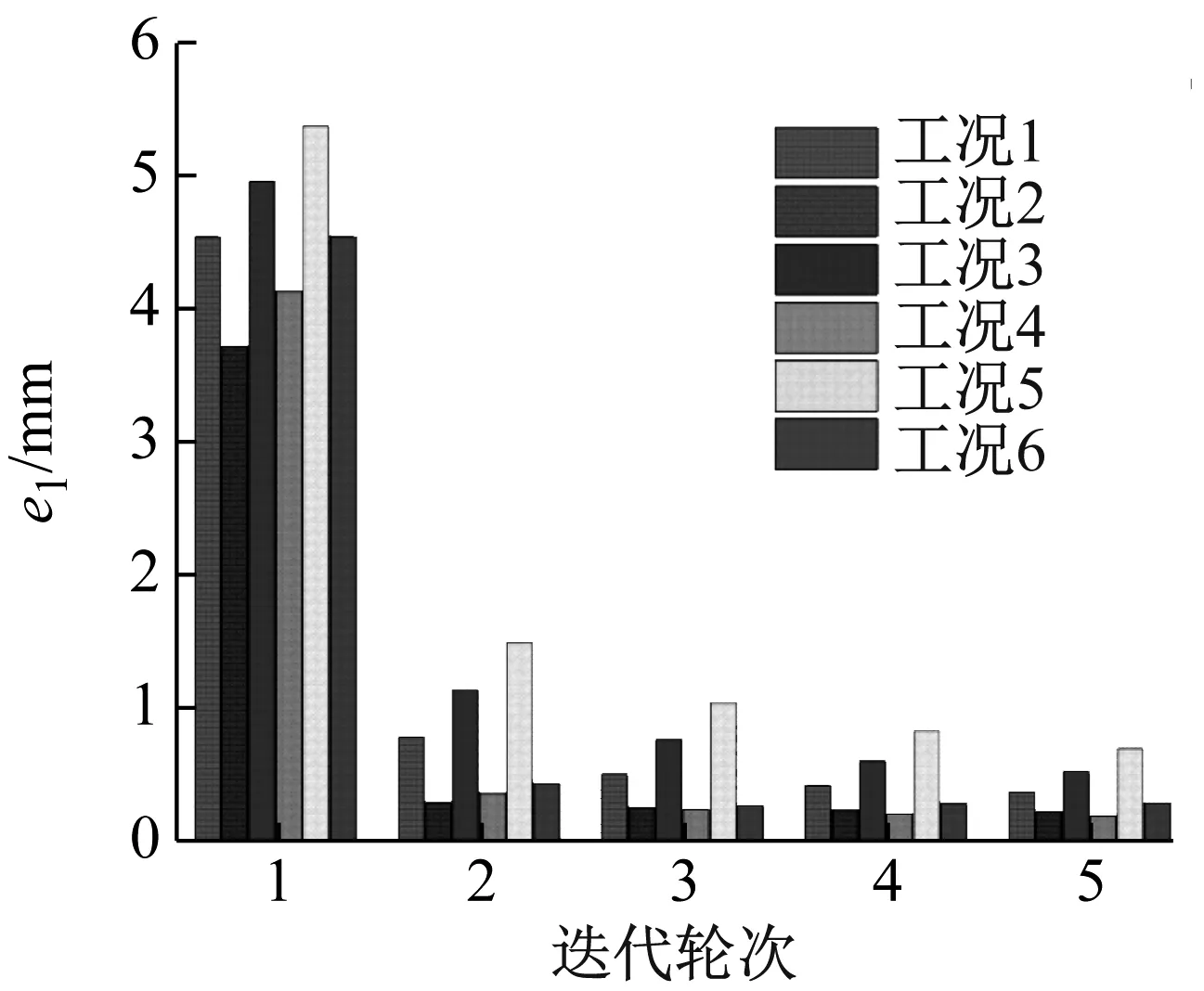
(a) 局部峰值误差

根据试验结果可知，物理加载时滞对迭代收敛性影响较大，位移预测补偿方法能有效提高迭代收敛速度与收敛精度，同时补偿精度的高低也在一定程度上影响着迭代收敛精度。

5 结 论

本文提出了考虑物理加载时滞的力修正迭代混合试验方法，针对三层框架-黏滞阻尼器减震结构进行数值模拟，主要结论如下：

(1) 相较于迭代混合试验，采用力修正策略的位移响应与参考解吻合程度较高，力修正能显著提高迭代收敛效率，同时力修正所采用的模型越精确，迭代收敛效率越高。

(2) 不同物理加载时滞的模拟结果表明，当时滞分别为15 ms,30 ms和45 ms时，在迭代5轮次内，有位移补偿策略均完全收敛，无位移补偿策略均处于不完全收敛状态；在迭代第5轮次结束时，对比无位移补偿策略，有位移补偿策略的局部峰值误差分别减小了39.09%,63.16%和58.87%，相对面积误差分别减小了29.99%,58.27%和65.53%，这表明物理加载时滞对迭代收敛效率影响显著，采用时滞补偿方法能有效提高迭代收敛速度与收敛精度。