基于遗传模拟退火算法的电动汽车充电调度方法研究

任小强

(西南交通大学希望学院，四川 成都 610400)

0 引 言

新能源电动汽车(Electric Vehicles ，EV)具有无污染、低噪音和高能效等特点，在降低环境污染和减少对化石能源的依赖方面具有较大潜力，已成为燃油汽车的重要替代品[1]。与燃油汽车相比，EV在大规模推广过程中，仍面临诸多问题，例如续行里程不足[2]、需要频繁充电、充电成本高等[3]，不确定的电动汽车无序充电方式容易影响车主的出行体验和充电效率[4]。此外，大量EV的无序充电还会导致充电桩利用率低、给电网带来巨大的负荷压力，从而影响充电站的安全运行和车主的充电体验。因此，如何对充电站内的EV进行合理的充电调度是一个亟待解决的问题。许多学者和专家对EV的充电调度问题进行深入研究，并取得了不错的研究成果。例如高建树等[5]以车辆数量和充电时长为目标，构建电动车辆充电调度模型，并采用多目标粒子群优化算法(Multi-Objective Particle Swarm Optimization，MOPSO)对模型进行求解，能够有效降低EV的充电等待时长和充电成本，但未考虑充电站的成本。刘岩等[6]构建了EV的动态多目标充电调度模型，并使用动态粒子群算法对模型进行了求解，能够起到降低电网负荷压力的效果，但未考虑车主的充电满意度。侯尚武等[7]建立了有序充电调度模型，并利用遗传算法求解该模型，该模型可通过实时电价的有序调度缓解负荷波动，降低峰谷电价，但未完全考虑到EV的实时充电需求，同时所设计算法的复杂度高，在实际应用中还存在一定的局限性。李春亭等[8]引入动态调整策略的蝙蝠算法解决EV停车充电优化调度问题，能够更好地适应EV的实时充电需求，能够实现更好的调度效果，但在求解过程中容易陷入局部最优。避免陷入局部最优的有效方式是融合两种以上算法，已被广泛应用到纸张表面缺陷智能化检测[9]、舰船分段装载顺序优化[10]、刀具准时化配送路径规划[11]、舰船资源装配效率优化[12]和有机磷农药残留检测[13]。因此，为了对电动汽车技术的不断发展提供理论支持和实践指导，本文提出一种基于遗传模拟退火算法(Genetic Simulated Annealing Algorithm，GASA)的EV充电调度模型，并与无序充电调度和其他优化算法进行对比，用以验证GASA算法的预测性能。

1 问题描述及模型构建

当EV进入充电站并连接充电桩后，充电调度系统获取车辆的到达时间、离开时间、已行驶里程数以及预期离开时间，同时结合充电站费用和配电网电价，对EV充电进行有序控制，以实现充电站运营商的利润和车主满意度最大化为目标。充电调度系统采用离散时间控制模式，将一天划分为144个调度时间段，用Δti(i=1，2，…，144)表示第i个充电调度时间段。该模型文中所用符号及含义如表1所示。

表1 主要符号及其含义

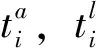
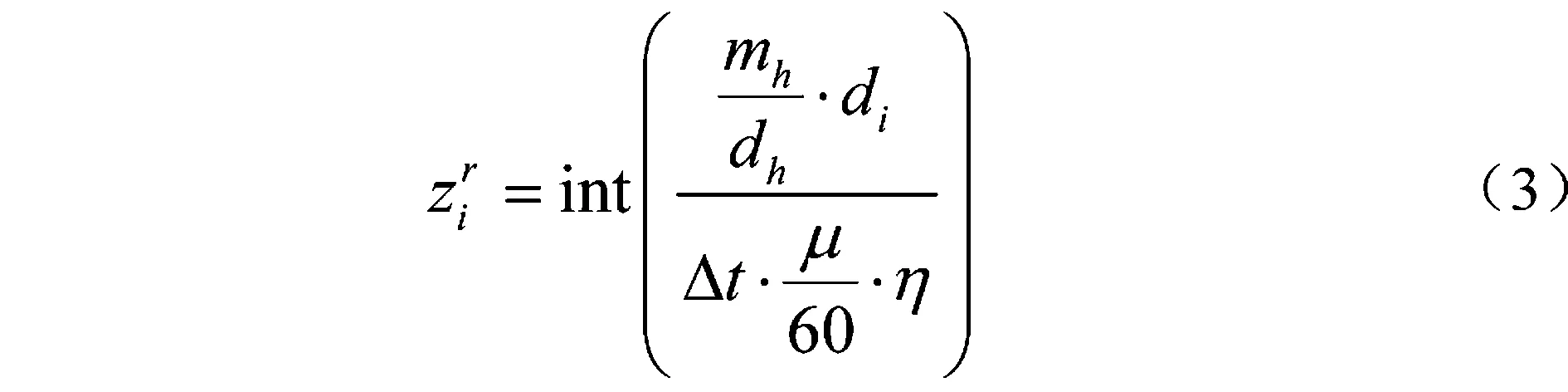
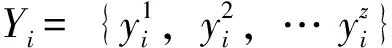
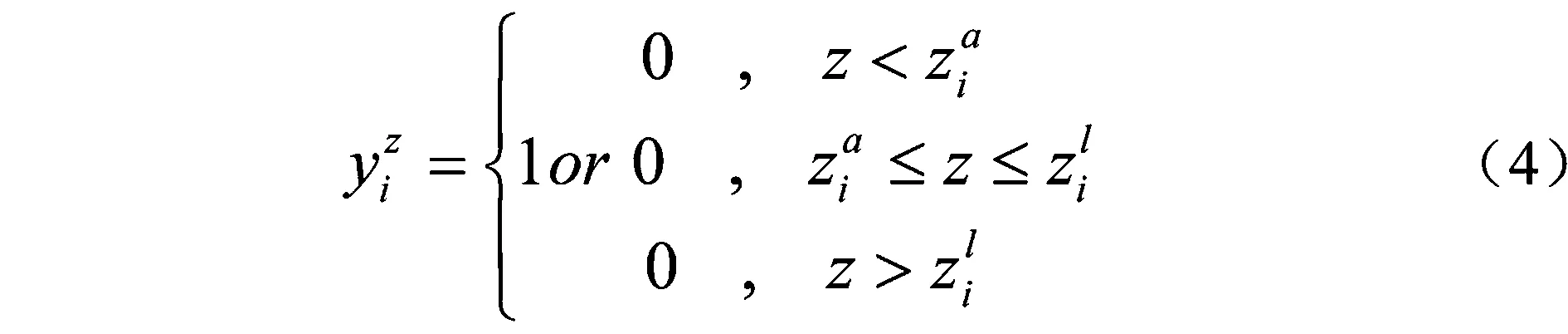
停车场运营商的利润由其向电网支付的购电费用和车主向其支付的充电费用两部分组成，如式(5)所示。

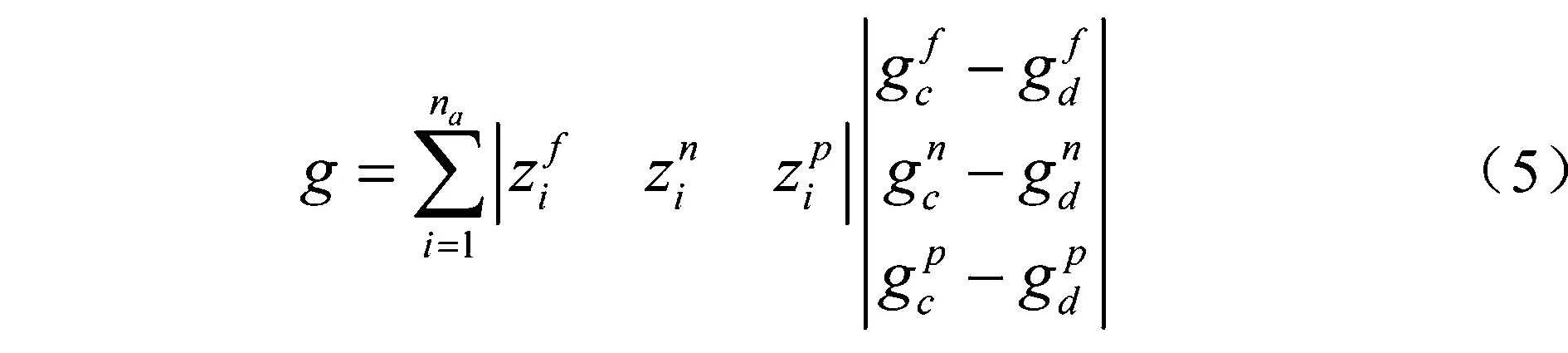
车主满意度包括费用满意度、时长满意度和惩罚函数，如式(6)和式(7)所示，其中σ为惩罚系数。

目标函数如式(8)～式(10)所示，其中a、b为权重系数。约束条件如式(11)、式(12)、式(13)所示，式(11)表示最多可为m辆EV同时充电，式(12)表示允许进入的EV，最终充电量要满足其需求，式(13)表示所有充电的EV能够在离开前完成充电需求。

2 遗传模拟退火算法设计

2.1 GASA算法

遗传算法(Genetic Algorithm，GA)是一种通过模拟自然进化过程搜索最优解的方法，最早由美国的John Holland于20世纪70年代提出，具有较强的全局寻优能力，但局部搜索能力较差，易陷入局部最优和出现过早收敛等问题。模拟退火算法(Simulated Annealing，SA)来源于固体退火原理，它原理简单，参数较少会以一定概率接受比当前解更差的新解，从而跳出局部最优，该算法具有较强的局部搜索能力，但对全局信息了解不多并且寻优速度较慢。针对这两种算法存在的优势和不足，本文提出一种遗传模拟退火算法(Genetic Simulated Annealing Algorithm，GASA)，将SA算法的Metropolis准则融入GA算法的交叉和变异操作中，提高GA算法的局部搜索能力，防止其陷入局部最优。GASA算法的具体步骤如下：

2.1.1 编码方式

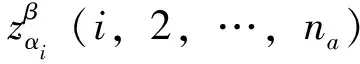
假设有5辆EV，表2列举了一种编码方式，其中第5辆车在第112、119、120及143个时间片充电，第4辆车在第34、67、70、78及120个时间片充电，第3辆车在第56、78、79及80个时间片充电，第2辆车在第4、5、19及27个时间片充电，第1辆车在第1、4及7个时间片充电。

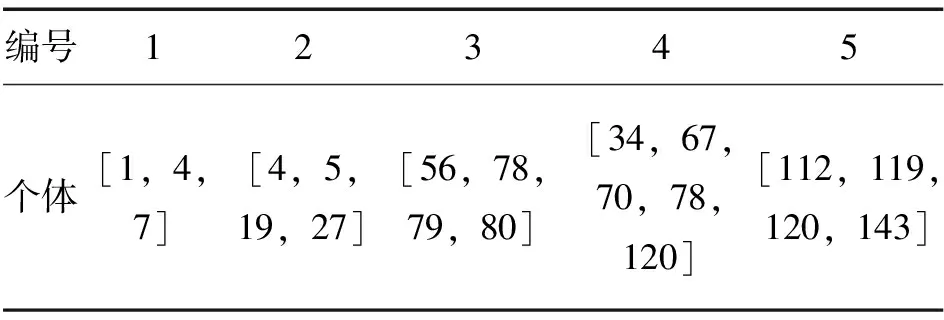
表2 编码方式

2.1.2 初始化种群

2.1.3 适应度函数

将式(12)所示的目标函数视为GA算法的适应度函数。

2.1.4 选择操作

选择操作的目的是把适应度函数值最优的个体直接遗传到下一代，采用锦标赛选择方法，每次从初始种群中随机选取δ个适应度函数值最高的个体，组成下一代种群。

2.1.5 交叉操作

交叉操作是指将两个父代个体的部分基因交换，以产生新的子代个体。采用两点交叉方式，即在(0，1)内生成的随机数，如果小于Pc，则执行两点交叉操作。

2.1.6 变异操作

随机生成(0，1)内的随机数，若小于预先设置的Pm，则进行变异操作，否则不执行。如果个体可行，随机选择一个分位，执行变异操作；如果个体不可行，则选择不满足约束条件最多的时间片分位进行变异操作。同时，为了避免GA算法的早熟情况，选用SA算法的Metropolis准则对交叉算子和变异算子得到的结果进行模拟退火处理，其中，Metropolis准则定义如式(17)所示，其中，Pm为接受概率，f1为交叉、变异后个体的适应度函数值，f2为交叉、变异前个体的适应度函数值，t0为当前温度，τ为迭代次数，tm为温度控制参数。

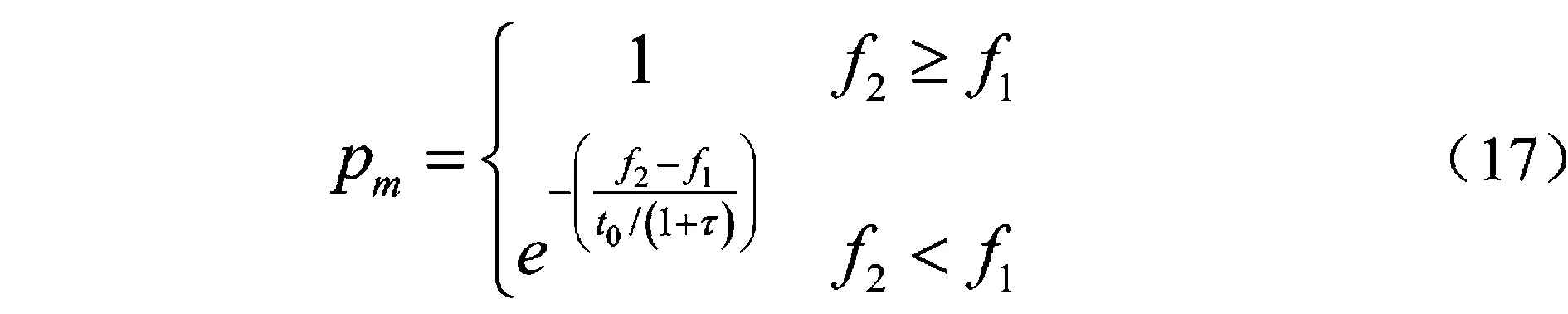
2.1.7 自适应交叉、变异策略

为了提高GASA算法的自适应能力，避免早熟收敛，加快收敛速度，使用动态自适应交叉概率Pc和变异概率Pm，如式(18)和式(19)所示，其中，kc、km为区间[0，1]内的常数，fa为种群的平均适应度函数值，fmax为最大适应度函数值，fc为交叉个体的适应度函数值，fm为变异个体的适应度函数值。μ为修正因子，如式(20)所示，其中ψ为调整系数，取值范围为区间[1，5]内的整数。

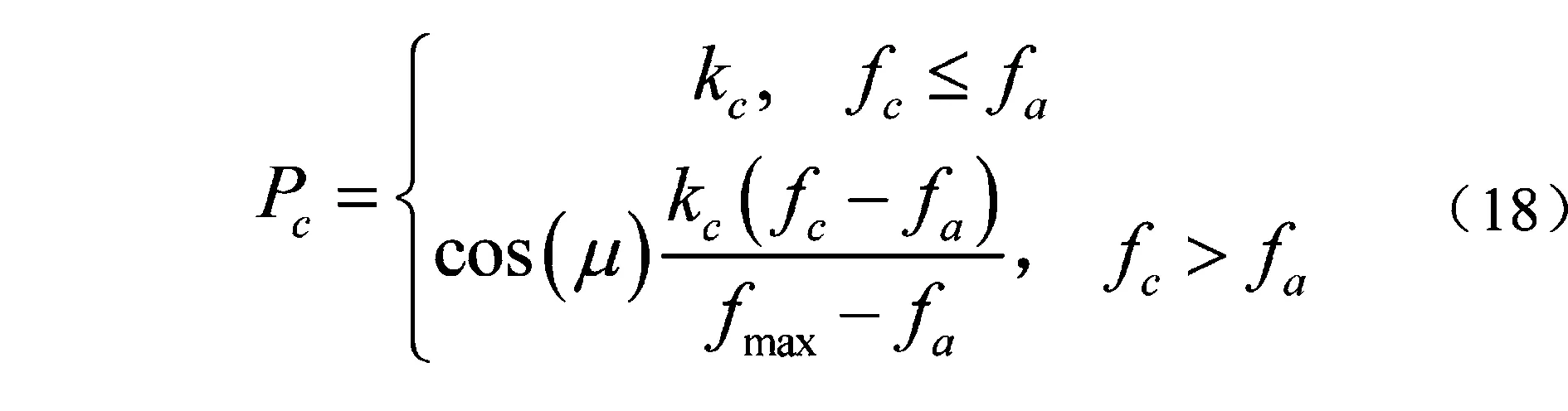
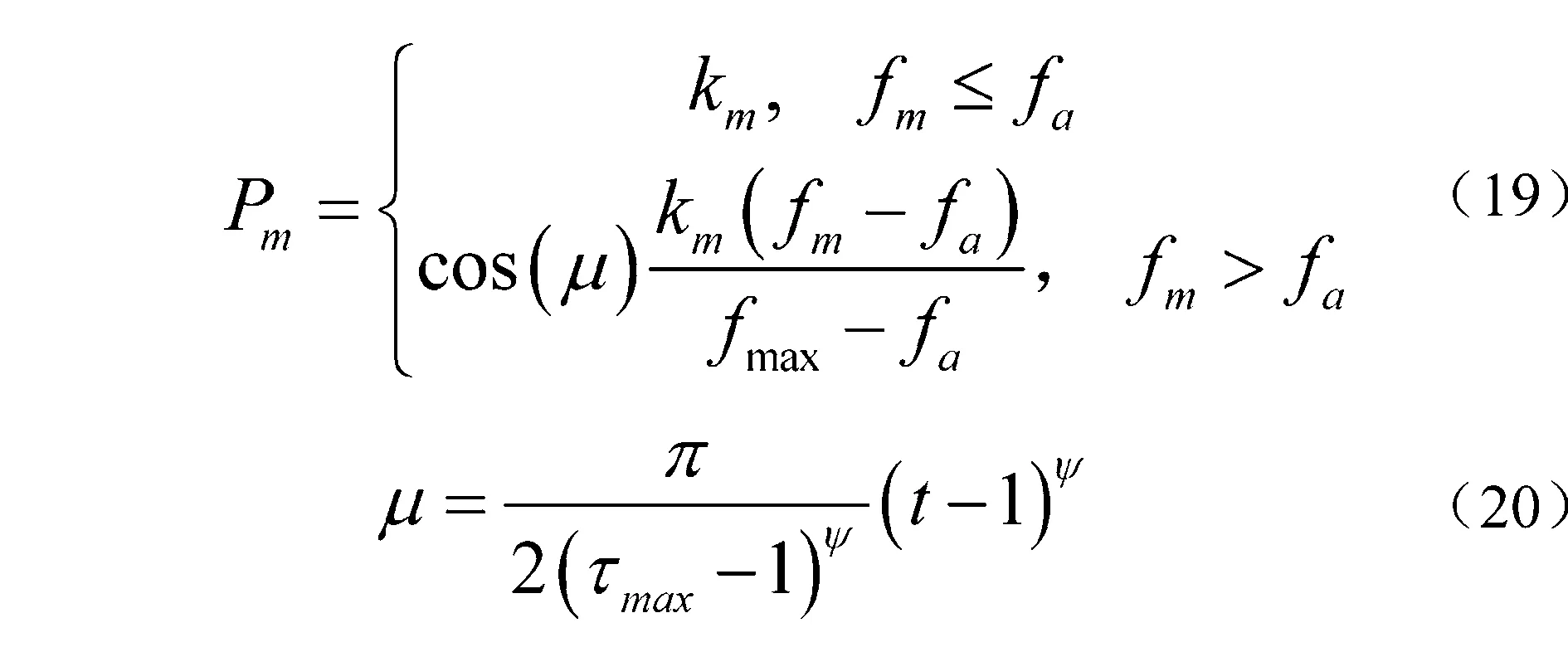
2.2 算法流程

基于以上所述，提出的基于GASA算法的电动汽车充电调度策略流程如图1所示。

3 仿真实验

3.1 仿真环境及参数设置

为分析验证本文设计的GASA算法在处理电动汽车充电调度的有效性和可行性，使用文献[14]中的GA算法、文献[15]中的SA算法和本文提出的GASA算法，分别求解300辆、400辆、500辆和600辆电动汽车的充电调度问题。为了使实验结果更加可靠，每种算法进行50次独立实验，将平均值作为最终结果。GASA相关的参数和电价的参数设置[16]如表3和表4所示，GA算法和SA算法的参数设置同文献[14]和文献[15]。

图1 充电调度策略流程图

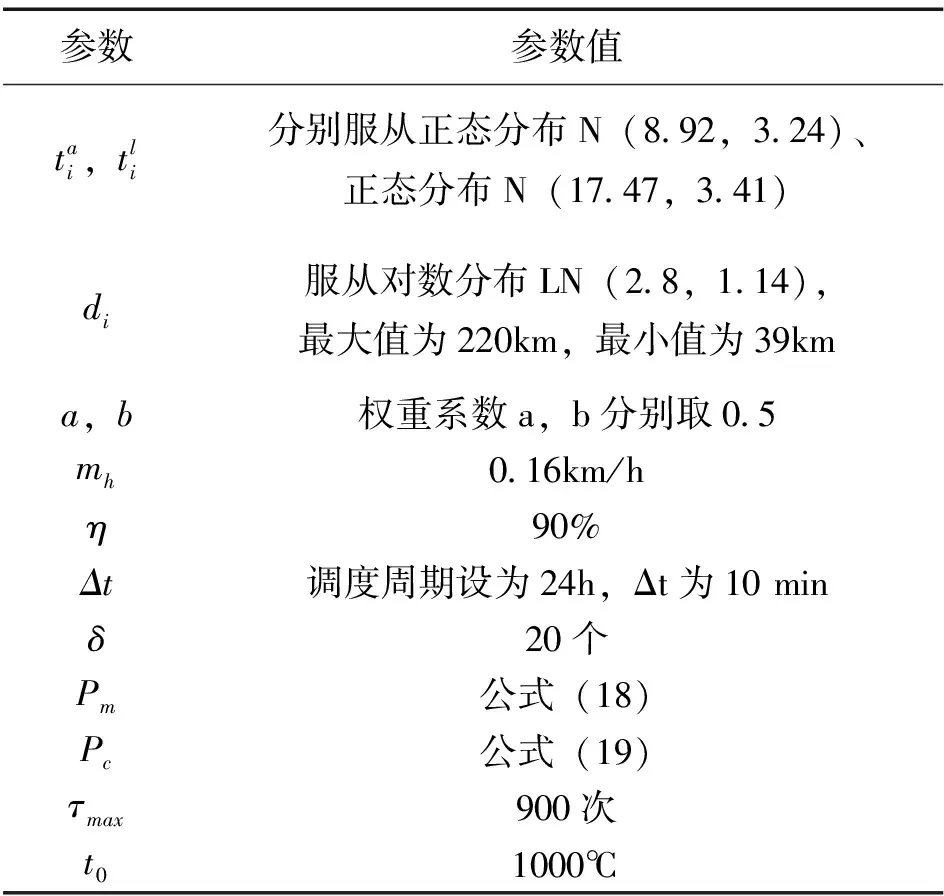
表3 算法的参数设置

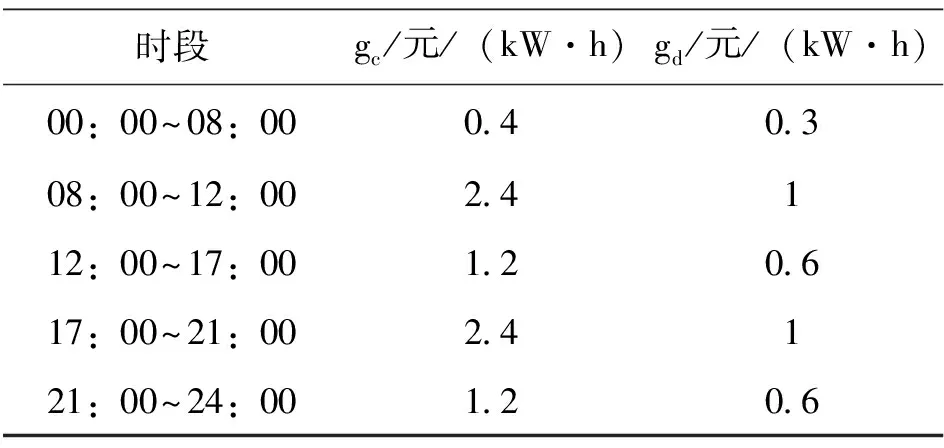
表4 电价参数设置

3.2 实验结果与分析

实验1：仅考虑停车场利润时的仿真结果如图2所示，横坐标为车辆数，纵坐标为停车场运营商的利润偏差率，基准值为车辆在无序充电调度下的利润，车辆数为300、400、500和600时，对应的基准值分别为2820、3660、4184和4425元。由图2可知，当车辆数为300辆时，利润偏差率为负，这是由于充电桩数量远大于车辆数，车主可以随意选择其中的充电桩对车辆进行充电。随着车辆数的增加，停车场运营商利润偏差率逐渐上升，算法的优势逐渐体现出来。当车辆数固定时，GASA算法的利润偏差率最大，GA算法和SA算法比较接近，这说明GASA算法的仿真结果要优于GA算法和SA算法。

实验2：仅考虑车主满意度的仿真结果如图3所示，横坐标为车辆数，纵坐标为车主满意度偏差率，基准值为车辆在无序充电调度下的满意度，车辆数为300、400、500和600时，对应的基准值分别为274、371、331和223。由图3可知，当车辆数为300辆时，满意度偏差率为负，原因同实验1。随着车辆数的增加，车主满意度偏差率逐渐增大，当车辆数为600时，GASA算法的利润偏差率高达75%，GA算法和SA算法为68%和67%，可以看出，GASA算法的性能最好。

实验3：综合考虑停车场利润和车主满意度仿真结果如图4所示，横坐标为车辆数，纵坐标为函数适应度值偏差率，基准值为车辆在无序充电调度下的适应度函数值，车辆数为300、400、500和600时，对应的基准值分别为0.5398、0.5377、0.4649和0.3821。由图4可知，当车辆数为300辆时，函数适应度值偏差率为负，原因同前。随着车辆数的增加，GASA算法的优势逐渐体现出来，当车辆数为600时，GASA算法的函数适应度值偏差率高达41%，SA算法和GA算法较为接近，分别为35%和32%。这说明GASA算法相较于SA算法和GA算法，仿真结果最优。

图2 停车场运营商利润对比

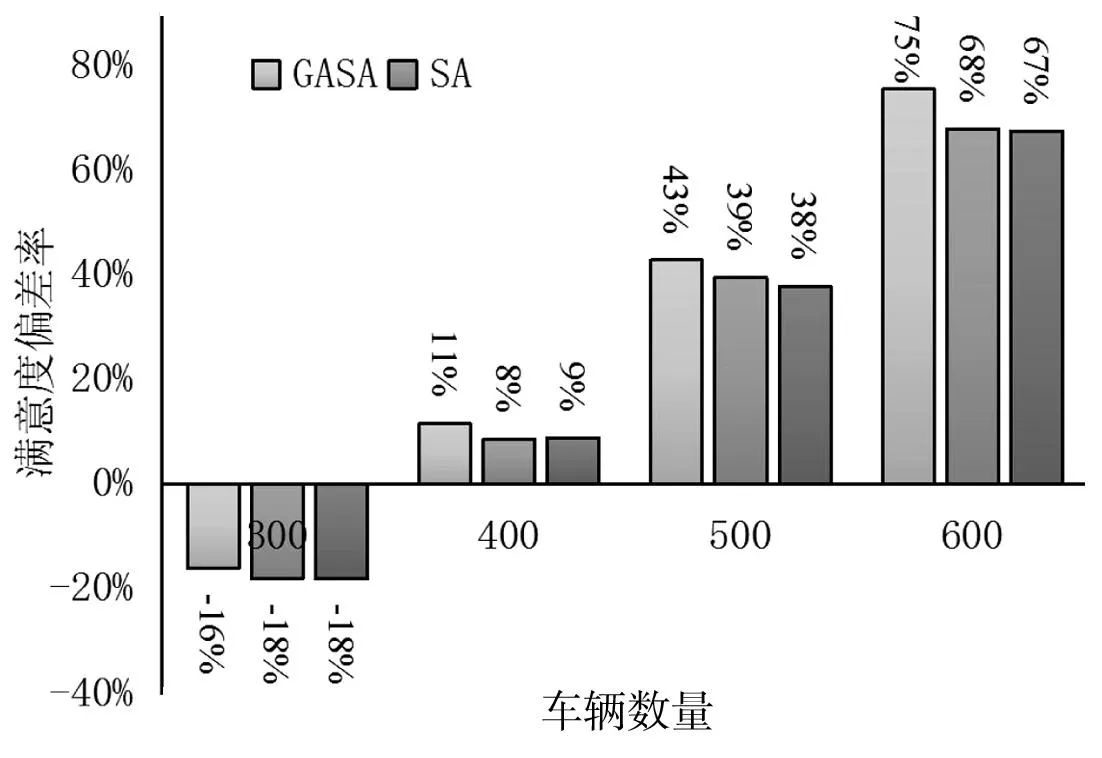
图3 车主的充电满意度对比

实验4：假设车辆数为400，GASA、SA和GA算法的收敛速度如表5和图5所示。从表3可以看出，GA算法陷入局部最优值0.318815；SA算法先陷入局部最优值0.316837后，然后跳出局部最优，最后收敛于0.317845；GASA算法跟SA算法类似，先陷入局部最优值0.317448，最后收敛于0.319542。由图5可知，随着迭代次数的增加，三种算法逐渐收敛，但收敛时，三种算法的迭代次数不同，GASA算法迭代到150次时，逐渐收敛；SA和GA算法迭代到250次时，才逐渐收敛。并且收敛时，GASA算法得到的适应度函数值高于GA及SA算法。因此，相较于另外两种启发式算法，GASA算法的性能更好。

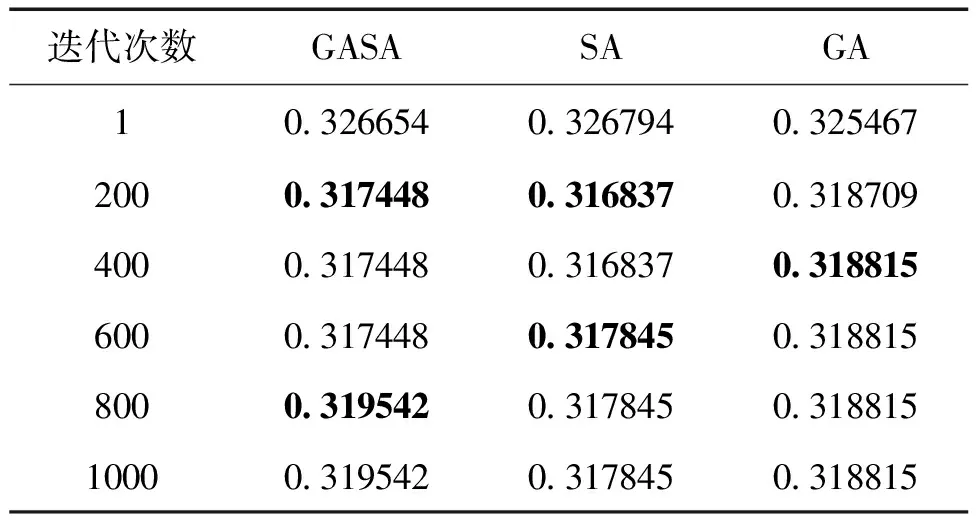
表5 三种算法的收敛速度对比表

图4 函数适应度值对比

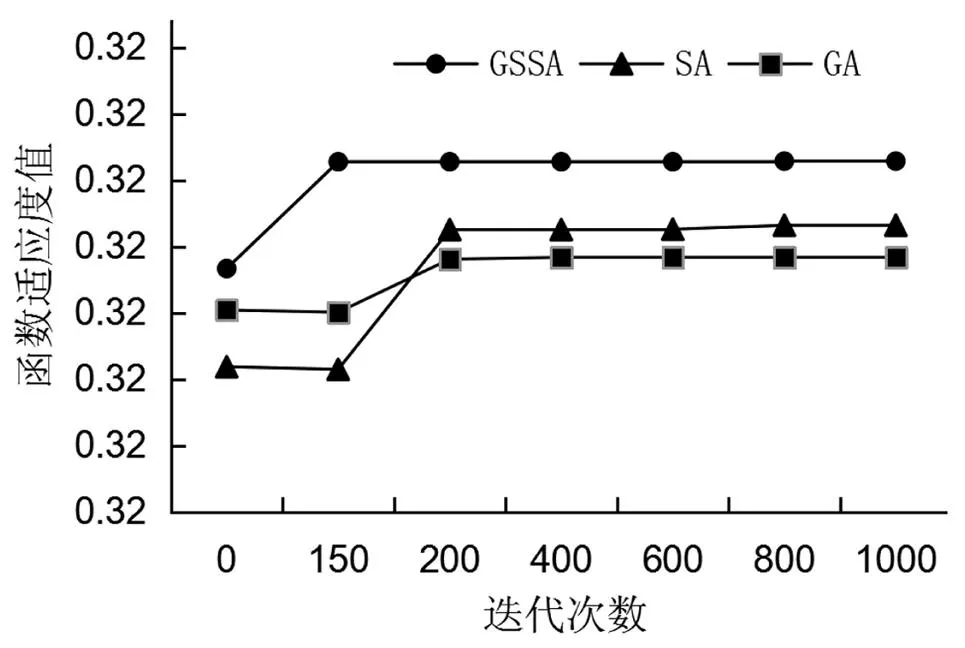
图5 三种算法的收敛速度对比

4 结 语

本文以充电站运营商的利润和车主满意度最大化为目标，构建充电调度模型，并使用遗传模拟退火算法求解。实验结果表明，遗传模拟退火算法在求解电动汽车充电调度模型时，具有显著效果，可以有效提高充电桩的利用率和用户的充电体验，对推动电动汽车行业的发展具有积极作用。后续研究中，继续围绕遗传模拟退火算法进行改进，进一步提升算法的稳定性和收敛速度；同时考虑更多的实际因素，例如充电站的空间分布、车辆行驶模式、充电模式以及在更广泛场景下的算法应用。