组合模型在膨胀土地区地铁站沉降预测中的应用

周煜程

(浙江省数智交院科技股份有限公司，浙江 杭州 310000)

0 引 言

在地铁车站施工中，基坑周边地表沉降是至关重要的监测项目，而沉降预测将帮助监测人员提前预知一系列沉降数据包括累计沉降量和沉降速率等的未来走势并作出相应的应对措施。因此，开展沉降预测的研究具有很强的工程应用价值。为提高预测模型的准确性，现有研究主要集中在两方面：一方面是提升预测模型中参数的准确性[1]；另一方面是尝试使用不同的单一模型，如双曲线法[2]、Asaoka法[3]、小波神经网络[4]、BP神经网络[5]等对地表沉降进行预测，选取更贴合实际的模型。前人的研究取得了明显的成果，但这些模型方法各有优势和不足，而通过多种模型的组合进行沉降预测的探究鲜有耳闻。

Granger C W J和 Bates J M首次提出组合预测方法[6]，认为即使某个单一预测模型效果不佳，但如果它包含目标系统的信息，当它和另外一个预测模型进行组合之后，同样可以增加整个预测系统的性能。不同模型的组合预测，能同时考虑不同预测模型的特征信息，相比于单一模型，组合预测模型对实测数据内部的变化规律能更加完善的吸收，能显著减小单一模型受外界不确定性因素影响而导致不精准的问题，有助于提高预测的精确程度和模型整体的稳定性和适用性。

根据膨胀土地区地铁车站基坑施工时的地表沉降变化规律，选取与此规律相似的S型成长曲线模型和饱和曲线模型进行深入分析，并通过matlab分别用Usher曲线模型(S型成长曲线的一种)和饱和曲线模型对实测沉降数据进行拟合，最终在此基础上提出一种相比于单一模型更为精确的组合预测模型，取得良好的预测效果。

1 膨胀土地区施工期的地表沉降

合肥市是我国膨胀土覆盖的典型地区之一，除沿现代河流分布的一级阶地之外，合肥地区广阔的波状丘陵均由膨胀性粘土构成[7]。

通过对膨胀土地区地铁车站基坑施工时的大量地表沉降数据的观察发现，虽然受施工工况的影响，但总体上地表累计沉降量总是随着开挖深度(时间)的增加而单调增加，且在开挖和基坑降水过程中会出现一个快速增加的过程，在s-t曲线上呈现出较大的斜率，并随着施工的结束，沉降量的增加逐渐减缓，最终趋于一个极限值。

如图1和图2所示，分别为合肥地铁东一环地铁车站基坑开挖施工过程中DB-02-02测点、合肥地铁宿州路地铁车站基坑开挖施工过程中DB-10-02测点的沉降实测数据。可见曲线大体上具有一种反S型的走势，与S型成长曲线十分相似。

S型成长曲线原本主要用于对社会自然经济的预测之中，这种曲线根本上反映的是一种事物从发生、发展到成熟，最终达到一定极限的过程。这同基坑沉降与时间之间的发展规律一致，宰金珉和梅国雄等[8]已经指出沉降与时间的关系呈现出一种S型规律。

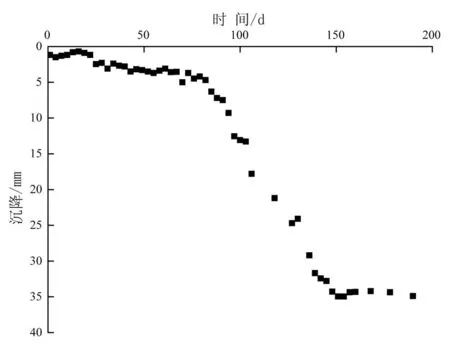
图1 合肥东一环地铁站DB-02-02测点沉降曲线

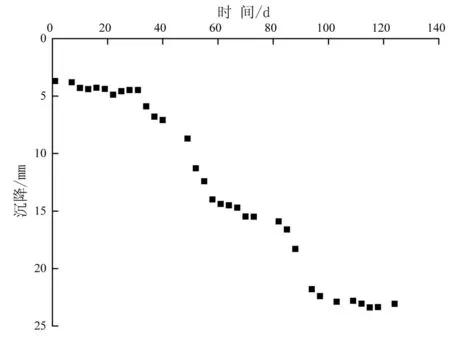
图2 合肥宿州路地铁站DB-10-02测点沉降曲线

2 Usher曲线和饱和曲线模型的选取

2.1 Usher曲线模型选取

时间与膨胀土地区地表沉降的关系符合S型成长曲线的变化规律，而成长曲线有多种类型，目前学者常用的4种表达形式如式(1)～式(4)所示。

Usher模型：

(1)

Logistic模型：

(2)

Gompertz模型：

S(t3)=ae-be-ct

(3)

Ratkowsky模型：

(4)

其中，S为总沉降量，t为时间，a为曲线的渐近线暨最大沉降量，c为沉降曲线增长速度参数，d为沉降曲线形状参数。

根据以上代数式，Logistic模型、Gompertz模型以及Ratkowsky模型实际上均是Usher模型的特殊情况：当d=1时，S(t1)=S(t2)；当d→∞时，S(t1)=S(t3)；当d=1且b1=eb4时S(t1)=S(t4)，因此本文选取Usher模型作为S型成长曲线的代表应用到组合预测之中。

2.2 饱和曲线模型选取

近年来有学者提出用饱和曲线来预测地表沉降的规律[9]。而将其应用到地表沉降预测中时，其表达式如式(5)所示。

(5)

其中，S为地表总沉降量，t为时间，a为曲线的渐近线暨最大值，b为曲线形状因子，c为曲线斜率因子[10]。

该模型具有的特点：单调性，S随t的增加而单调增加，并最终趋于最大值a；有界性，t→0时，S→0；t→∞时，S→∞；存在反弯点，开始时曲线较缓，中段坡度较大，最终斜率趋于0并且达到最大值。

可见饱和曲线模型的变化规律与S型成长曲线类似，也和实际工程中地表沉降与时间的关系十分相似。

综上所述，本文将Usher曲线模型和饱和曲线模型确定为组合预测模型的两个组成部分。

3 预测模型的建立

选取合肥地铁龙岗大道站DB-13-03测点的监测数据，探究独立的Usher曲线模型和饱和曲线模型的预测效果。监测人员每3d进行一次地表沉降监测。针对地表沉降全过程呈现“S”型的规律，最需关注的就是中间斜率最大，也就是沉降速率最大的区段。工程监测时间段中，自40d之后累计沉降量进入快速增加阶段，是最需要做出预测的。因此，选择将第43d至第55d共5次监测作为预测区间段，第43d前的监测点数据作为建立预测模型的基础拟合数据，具体方式如下：首先取整个监测过程中沉降变化较为明显的55d共19次的监测数据作为研究对象，并将这些数据分为2组，第一组为拟合组(作为两个单一模型拟合表达式的确定依据)：包括1d到40d共14次监测；第二组为预测组(作为组合模型预测效果的检验依据)：包括43d到55d共5次监测。在此基础上分别将两个模型前40d拟合段中各个拟合时间节点上的拟合值与实测值进行比较，并以其相对误差的平方作为考量而得到两者的权重系数，从而建立饱和曲线-Usher曲线组合预测模型，最终分析这种组合模型的预测效果是否较单一模型有所提高。

3.1 单一模型表达式参数的确定

在确定组合预测模型的表达式之前，需首先确定单一模型的具体权重。matlab拥有强大的数据处理功能[11]，使用其中的Curve Fitting tool工具来进行非线性拟合如图3所示。

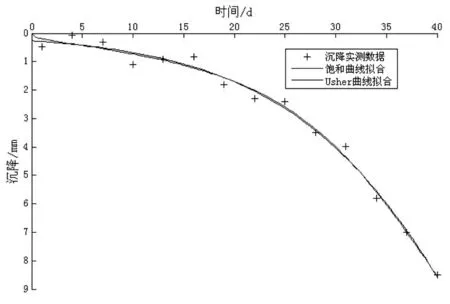
图3 单一模型对1d到40d拟合段的拟合情况

可见，两个独立模型对于1d到40d拟合段的数据拟合效果均较好，能反映地表沉降随时间的变化规律。通过输入的数据，matlab得到了饱和曲线S(t)和Usher曲线U(t)各自的拟合曲线如式(6)和式(7)所示。

(6)

(7)

3.2 组合模型的建立

基于Granger C W J和 Bates J M的组合预测思想，本文将前述选择出的Usher模型和饱和曲线模型通过加权进行组合，并研究其预测效果。根据拟合出的代数表达式，可以得知任意日期的地表沉降拟合值。将各个监测时间点的地表沉降实测值和单一模型拟合值进行比较，获得各个时间点的相对误差，进而按照相对误差平方值的比值，确定某特定点任一模型的权重系数，详见表1(1d到40d部分数据)。对14组数据的权重系数进行平均得到Usher曲线模型的权重系数为0.499，饱和曲线的权重系数为0.501，组合预测曲线的表达式可简化为如式(8)所示。

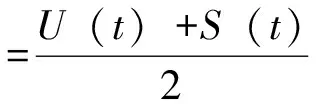
(8)

由式(8)得到预测组的组合预测值。具体情况如表1所示(43d到55d部分数据)。

表1 组合预测模型权重系数的确定与预测结果

3.3 组合模型的效果验证

由表1可见，对43d到55d期间的地表沉降预测，组合预测模型的绝对误差明显小于任何单一模型。0d到55d期间Usher曲线、饱和曲线、组合预测曲线与实测曲线如图4所示，在1d到40d拟合区间段，三条曲线都表现出相当好的拟合适用性，均和实测值近乎重合。但对于以这14组数据为基础而预测得到的预测段5组数据43d到55d，Usher曲线的总沉降量S增加速率过快，而饱和曲线的总沉降量S增加速率过慢并趋向于极限值，它们与实测数据均有较明显偏差。而饱和曲线-Usher曲线组合预测模型在49d、52d、55d三个时间节点的预测值和实测值近乎重合，相对于两个单一模型表现出明显的适应性和准确性。

图4 组合预测曲线与实测曲线

对模型进行可靠性检验是建立模型并且证明模型适用性不可或缺的一部分，未经可靠性检验的模型无法应用于工程实际。图像分析比较法[12]是模型验证的直观方式，将实测值和预测值作为x轴和y轴，通过角平分线作为准确性的参考。图像比较法的验证结果如图5所示。

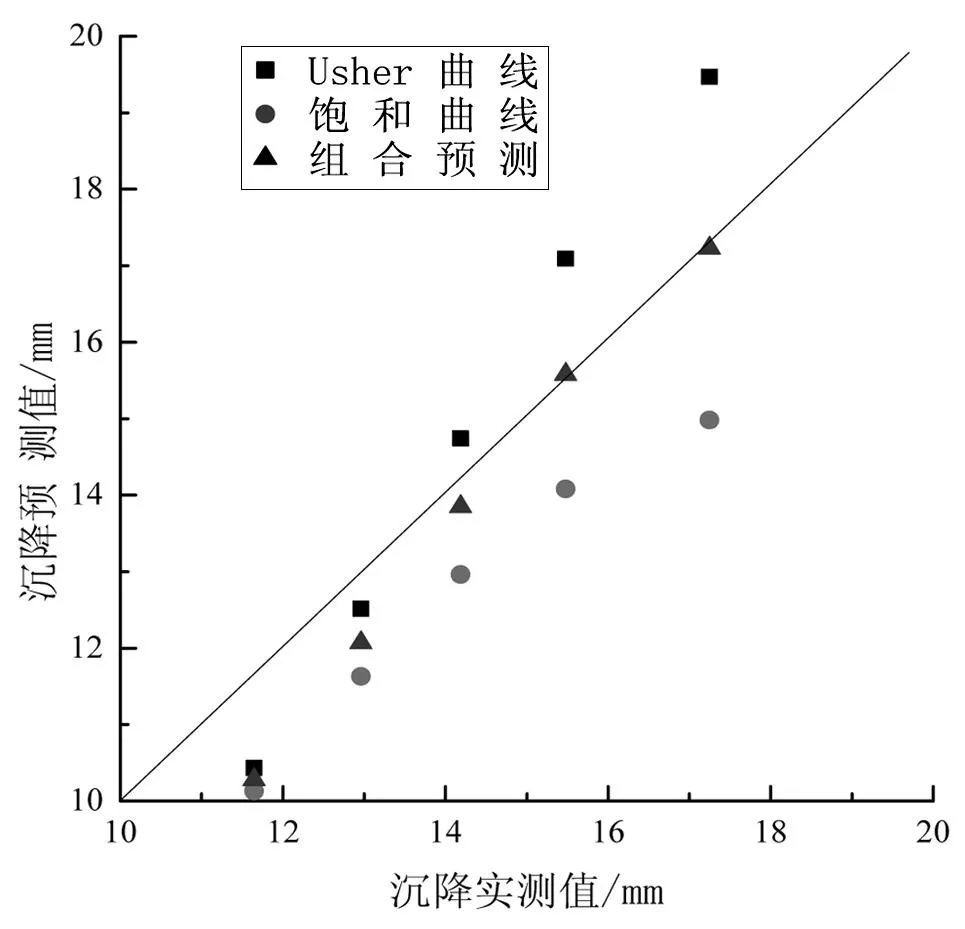
图5 图像分析比较法模型可靠性检验

由图5可知，组合模型的预测值有2个点落在预测值等于实测值的直线上，而单一模型的预测值则散落在远处并且有误差继续增加的趋势，说明组合预测相对于单一模型在很大程度上提升了预测效果。

此外，选取统计学参数：绝对误差平方和SSE、标准误差SE、准确因子Af来进行可靠性验证，如式(9)所示。

(9)

SSE越靠近于0，SE越接近于0，Af越趋近于1，则模型预测越准确。如表2所示，组合预测模型相对于单一模型的准确度至少提升了98%。

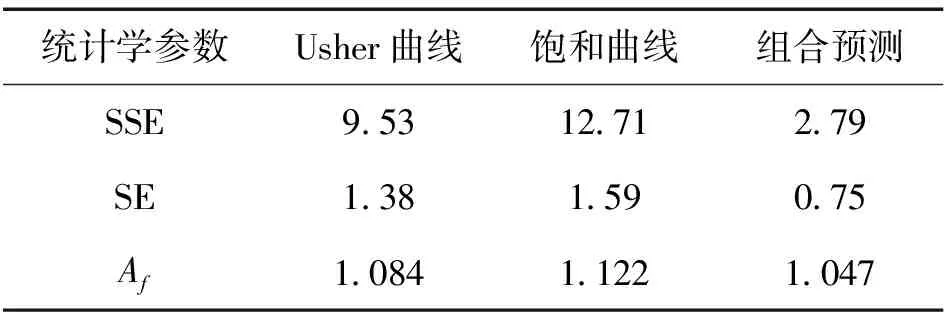
表2 单一模型和组合预测模型预测段统计学参数

4 组合预测模型工程应用实例

为了检验饱和曲线-Usher曲线组合预测模型式(8)在工程应用中的效果，另选取合肥地铁其它标段监测数据加以验证。图6是合肥地铁宿州路地铁站DB-10-03测点的地面沉降实测数据与三种模型预测值的对比，其中1d到22d为拟合段，25d到34d为预测段。

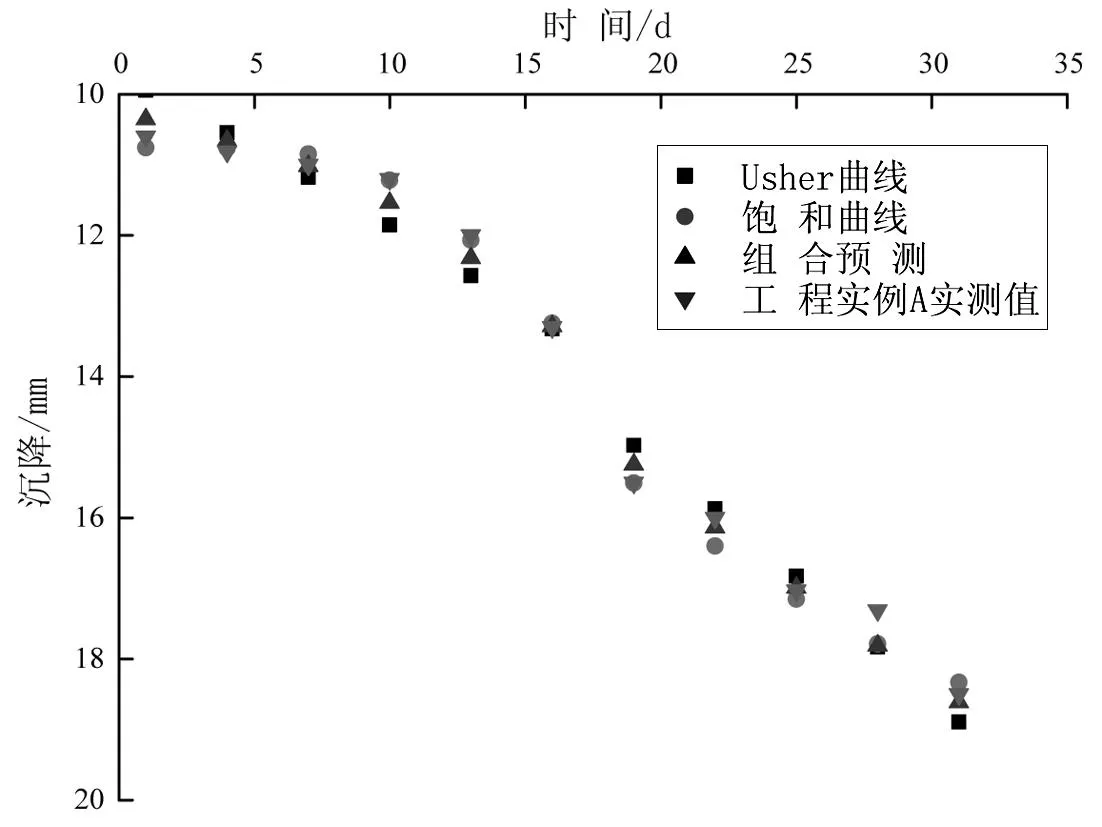
图6 宿州路地铁站地面沉降模型预测值与实测值

从工程实例可看出，在获得初期的沉降监测数据后，饱和曲线-Usher组合预测模型能较为准确地预测地表沉降未来走势，并相较于传统单一模型具有更高的预测准确性，可以给予工程测量人员有效参考，具有一定的工程应用价值。

5 结 语

(1)膨胀土地区地铁车站的地表沉降随着时间的推移，具有发生、发展、成熟最后达到极限值的变化特点，其地表沉降量-时间曲线与S型成长曲线和饱和曲线类似。

(2)对于膨胀土地区地铁车站的地表沉降数据，单独使用饱和曲线模型和Usher曲线模型的沉降预测效果较差，饱和曲线模型预测得到的沉降速率偏小，而Usher模型得到的沉降速率偏大。

(3)基于组合预测的思想，通过选取各个拟合时间节点的相对误差平方值作为考量，得到Usher曲线模型和饱和曲线模型在组合预测模型中的权重系数分别为0.499和0.501，从而建立饱和曲线-Usher曲线组合预测模型式(8)。这一组合预测模型相对于单一模型的准确度至少提升了98%，具有相对较好的预测准确度和工程应用价值。