面向图像识别的多层脉冲神经网络学习算法综述
2023-02-21李雅馨申江荣徐齐
李雅馨,申江荣,徐齐*
1.大连理工大学人工智能学院,大连 116024; 2.人工智能与数字经济广东省实验室,广州 510335;3.浙江大学计算机科学与技术学院,杭州 310058
0 引 言
第1个脉冲神经网络(spiking neural network,SNN)由Wolfgang Mass提出,由于其生物学上的可解释性,被誉为第3代人工神经网络。第1代神经网络是Rosenblatt于1958年提出的感知机模型,该线性模型可以用于解决简单的逻辑问题,但是难以表达更加复杂的非线性问题。第2代人工神经网络(artificial neural network,ANN)则引入非线性的激活函数,例如Rumelhart等人(1986)提出的前馈神经网络和误差反向传播机制可以用于解决复杂问题。上述人工神经网络模型缺乏一定的生物可解释性,例如无法模仿生物神经网络的学习机制等,因此提出了更加接近于实际生物神经元的第3代人工神经网络——脉冲神经网络。SNN是基于脉冲神经元构建的网络模型,通过脉冲序列中的时间和空间信息来传递特征信息,模拟了生物神经系统中的突触建立、增强与抑制的工作机制,SNN将生物工作原理和数学模型结合起来,构建兼具生物可解释性和计算高效性的神经网络模型(胡一凡 等,2021)。
ANN在图像识别领域已有广泛应用, ANN主要是利用连续的函数计算图像特征(黄铁军 等,2022),近年来,出现了很多ANN深度学习模型,如ResNet (residual network)、VGG (Visual Geometry Group)等,然而因为脉冲的二值性,SNN在训练上存在不可微等问题,SNN在一些大型复杂数据集上的性能稍逊于ANN模型,但是SNN受实际生物视觉神经系统启发,将图像像素编码成脉冲序列,从脉冲序列的时空信息中提取图像特征,在SNN训练时,脉冲神经元模拟生物神经元的工作机制通过传递脉冲序列来传递信息,更具有生物可解释性的优势,且其因为脉冲的异步性和稀疏性(Li等,2021),具有高效率低耗能的优点。脉冲神经网络的学习算法主要是基于生物神经网络工作机制的原理并结合ANN中的一些算法思想。根据训练数据的不同以及网络结构的不同,这里从监督学习和无监督学习的训练方法,以及其在深度脉冲神经网络中的相关研究3个方面讨论SNN相关学习算法。
1 脉冲神经元
1.1 HH模型
HH模型 (Hodgkin Huxley model) 是由Alan Hodgkin和Andrew Huxley于1952年提出的神经元模型(Hodgkin和Huxley,1952)。他们通过在乌贼的巨型轴突上进行实验,认为膜电势的产生主要与钾离子(K+)、钠离子(Na+)的转运过程促使细胞内的离子浓度与细胞外液中的离子浓度之间存在差异有关,还与一些其他的离子(如氯离子(Cl-))通过通道形成漏电流有关,因此HH模型试图刻画3种离子K+,Na+,Cl-对于膜电位产生的作用。
如图1所示,HH模型认为细胞膜可以起到存储电荷的功能,由于细胞膜内外的离子浓度差造成了电势差,而细胞膜上流过的电流主要由电导和离子的电势决定。C表示电容,EL,EK和ENa表示3种离子的平衡电势,电阻R,RK和RNa表示细胞膜允许离子通过的能力即电导g,电导与膜电位相关,I是外加电流。
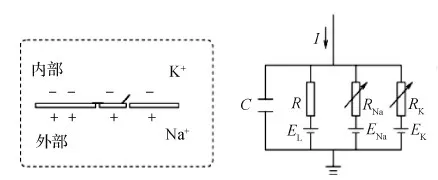
图1 HH模型 (Hodgkin和Huxley,1952)
上述离子通道有打开和关闭两种状态,用α表示关闭的通道打开的速率,β表示已经打开的通道关闭的速率,n、m、h分别表示K+、Na+、Cl-离子通道打开的概率,其更新为
(1)
(2)
(3)
式中,Vm表示膜电位,gNa、gK、gL表示3种离子通道的电导,则通过细胞膜的离子通道的电流之和可以表示为
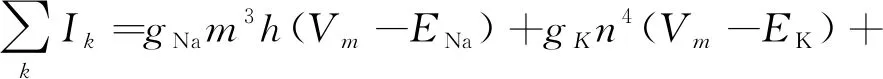
(4)
1.2 LIF模型
LIF模型 (leaky integrate-and-fire model) (Gerstner等,2014)相比HH模型更加简化,同时比传统ANN的神经元模型更接近于实际生物神经元的模型,是现有SNN最常用的模型之一。LIF模型将神经元的模拟电路简化为图2所示。
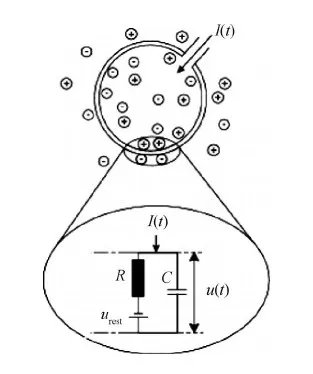
图2 LIF模型 (Gerstner等,2014)
LIF模型简化了各种不同的离子通道,将其作为一个整体,它的基本电路只包括两个部分:一个电容C和驱动电流I(t)电阻R,则电流I(t)可以表示为
I(t)=IR+IC
(5)
LIF模型中的leaky表示漏电电流,当电位值不超过阈值时会回到静息电位,integrate表示积分,表示该神经元受到的所有突触前神经元的电流刺激,fire表示发放,当电位值超过阈值就会发放一个脉冲。用Vm表示膜电位,Eleak表示平衡电势,gleak表示电导,当LIF神经元接收突触前神经元脉冲,膜电位上升超过阈值就会发放一个脉冲,然后回到重置电位,则会发放其微分方程,可以表示为
(6)
1.3 SRM模型
SRM模型 (spiking response model) (Gerstner等,2014)是由LIF模型推广而来,SRM模型没有固定的发放阈值,其阈值θ(t)是变化的,在SRM模型中用Vm表示膜电位,Vrest表示静息电位,用函数η来描述动作电位和动作电位之后的曲线,输入电流I(t)用k(s)过滤生成输入电位h,神经元接受突触前神经元的电流刺激,如果达到阈值,就发放脉冲序列S,如果发放了脉冲,阈值会增加。如图3所示。
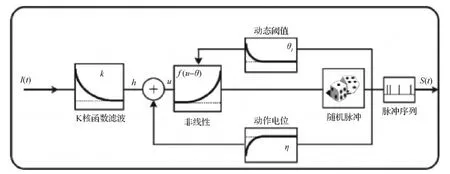
图3 SRM模型 (Gerstner等,2014)
SRM模型的膜电位变化可以表示为
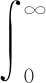
(7)
2 脉冲神经网络拓扑结构
在生物视网膜神经环路中,首先由视锥细胞和视杆细胞接受光刺激,然后由中层细胞将刺激传导至神经节细胞,神经节细胞的感受野可以感知图像特征,生物的视觉网络中会存在前馈,横向的连接,通过抑制和兴奋来控制细胞。受到生物神经网络的启发,提出了类似于神经细胞的前馈连接的多层感知机模型,后来又提出全连接、卷积和循环结构的神经网络模型,在SNN中也会存在这些结构,从最初的单层学习模型,后来提出适用于SNN的卷积核,并且也有研究循环结构的SNN。因此,SNN的网络拓扑结构分为3种:全连接、卷积和循环结构。
神经网络结构主要由输入层、隐藏层以及输出层组成。其中全连接的网络结构每个神经元接收上一期所有神经元的加权输入,将信号进行前向传播来提取特征;卷积的网络结构利用卷积核,类似于生物视觉系统中的感受野结构,对输入特征进行卷积操作来提取特征;循环的网络结构不仅接收前一层神经元的输入,还可以接收自己上一时刻的信息作为特征。
3 脉冲神经网络的无监督学习算法
无监督学习算法受生物神经网络中突触建立、增强和抑制的工作机制启发,在生物神经系统中,传递的是脉冲序列的时空信息,根据突触前后的脉冲刺激来增强或者减弱突触连接,利用这种生物学原理可以无监督地学习SNN的权值。Hebbian(1949)最早提出了突触可塑性的Hebb理论,即突触前神经元对突触后神经元重复持续的刺激,可以增强它们之间的突触连接强度。大多数无监督学习算法都是基于Hebb学习规则提出的,这种方法更具有生物可解释性。
STDP(spike-timing-dependent plasticity)规则是Hebb理论的扩展,Song等人(2000)基于STDP规则提出了一种脉冲时序依赖的学习算法,STDP规则根据突触前神经元和突触后神经元动作电位的相对时间来更新突触权重。如果突触前神经元发放脉冲的时刻比突触后神经元早,则称为长时程增强LTP(long-term potentiation),突触权重应该变大;如果突触前神经元发放脉冲的时刻比突触后神经元晚,则称为长时程抑制LTD(long-term depression),突触权重应该变小。
还有一些三脉冲的STDP方法,比如Pfister和Gerstner (2006)的triplet-based STDP,Shahim-Aeen和Karimi(2015)的TSTDP。与一般的STDP不同的是,三脉冲STDP包括一个突触前脉冲和两个突触后脉冲。
为了将STDP用于图片分类任务,Diehl和 Cook (2015)提出了将STDP算法用于手写数字识别,并且在MNIST (Modified National Institute of Standard and Technology)上达到了95%的准确率,该方法基于LIF模型,建立了具有输入层和处理层的神经网络。其中处理层的兴奋性神经元以侧边抑制的方式一对一连接到抑制性神经元,抑制性神经元连接到所有的兴奋性神经元,如图4所示。该方法利用三脉冲STDP训练,因为三脉冲STDP不使用权重依赖进行学习。
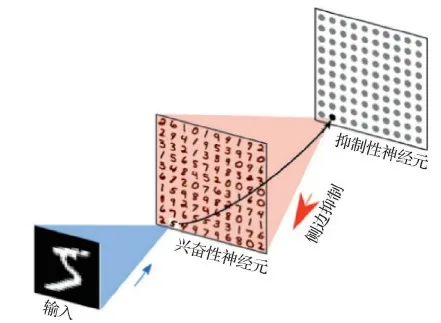
图4 基于STDP算法网络结构 (Diehl 和 Cook,2015)
此前研究中的STDP只有单层的,为了让其有更好的性能,Kheradpisheh等人(2018)提出了一种多层的基于STDP方法的SDNN(spiking deep neural network)网络,主要用于目标识别,利用时间编码设计了一种层数更深的SNN,包括若干个卷积层和池化层,且可以用STDP方法来训练,网络结构如图5所示,在MNIST上的准确率达到了98.4%。采用的是LIF脉冲神经元模型,每个神经元接收上一层突触前神经元的脉冲,如果达到膜电位阈值则发放脉冲,用Wj,i表示第j个突触前神经元与第i个突触后神经元连接的突触权值,在每个时间步,脉冲神经元的电位可以表示为
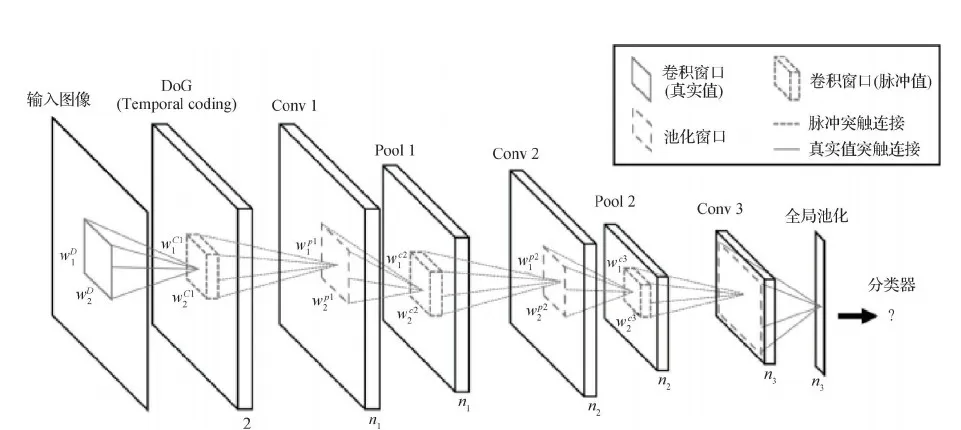
图5 SDNN网络结构图(Kheradpisheh等,2018)
(8)
如果突触前神经元在t-1时间步发放了脉冲,则Sj(t-1)为1,反之为0。用简化的STDP算法更新权重
(9)
式中,tj,ti是突触前神经元j和突触后神经元i脉冲发放时刻,a+,a-表示两种情况下的学习率。
Mozafari等人(2019)将奖励机制加入到STDP方法中,提出了R-STDP方法(reward-modulated STDP),该方法在MNIST上的准确率为97.2%。设计了一个3层的网络结构,其结构由Kheradpisheh等人(2018)方法改造而来,首先输入图像用差分高斯滤波器在不同尺度卷积,然后经过编码产生脉冲序列传递到下一层,经过多个卷积层和池化层,限制神经元每个时间步长只发放一个脉冲,最后一层决策神经元可以对应每个数字类别,由最早发放脉冲的神经元或者最大电位值来分类,根据最后一层分类结果产生奖励信号调节STDP系数。
在Diehl 和 Cook (2015)工作的基础上,Saunders等人(2018)提出了C-SNN(convolutional spiking neural networks),图像的特征可以在神经元亚群中共享,或者独立地演化以获取不同区域的不同特征。该模型以一种无监督的方式学习格点数据,小块的神经元可以共享参数也可以独立学习特征。模型采用的是一种改进的LIF神经元模型,利用内稳态的机制平衡整个网络,包括兴奋性神经元和抑制性神经元。C-SNN的结构如图6所示,k是核大小,s是步长,一个卷积块是一个兴奋性神经元的亚群和一个等大的抑制性神经元的亚群,输入空间的每个部分,与STDP可修改突触连接到兴奋性亚群的每个单个神经元,兴奋性神经元和抑制性神经元亚群一对一连接,如图6所示,即为提出的卷积SNN模型。其权值更新用的是online STDP。
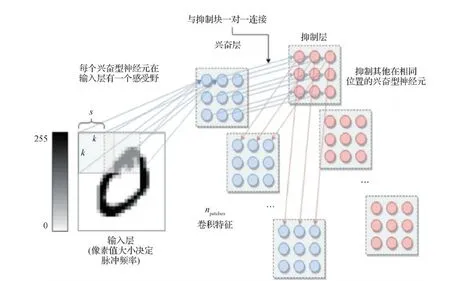
图6 C-SNN的结构 (Saunders等,2018)
有研究表明,贝叶斯原理在人类大脑处理信息的过程中会被用到,因此,Guo等人(2019)提出了一种赢家通吃(winner-take-all,WTA)策略的层次网络,该网络基于脉冲的变分期望最大化算法。该算法有两个步骤,首先是基于脉冲的变分E步,将层次WTA动力学脉冲响应作为平均场方程优化先验概率和平均场分布之间的KL(Kullback-Leibler)散度;然后是基于脉冲的变分M步,用STDP规则随机收敛到下界的极大值。并且在MNIST数据集上达到95%的准确率。
Liu等人(2020)提出了一种时间连续的模型MPN(the McCulloch-Pitts network),用于学习脉冲序列,这个模型是基于一个局部的学习规则,定义了更新连续时间SNN的状态和权值的规则,并证明了给定的一对突触前和突触后神经元的权重变化的曲线与STDP的曲线相似,如图7所示。该模型更具有生物可解释性,可以学习二进制向量的序列或者脉冲的时空特征,可以稳健地学习记忆二元向量的多个时空模式,扩展了对称Hopfield网络的记忆静态空间模式的能力。
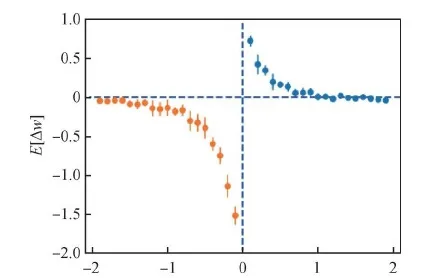
图7 一对MPN脉冲神经元生成的曲线图(Liu等,2020)
受生物自组织过程的启发,Lyu等人(2021)提出了一种在训练网络的过程中在神经元之间建立新连接的方法,利用LIF模型,基于电导的突触和STDP规则构建了一个4层的前馈网络,基于突触前和突触后神经元脉冲时间差,可以在隐藏层中建立新的突触连接,并利用STDP规则来更新突触权值,在输出层引入赢家通吃机制。
结合信息论的思想,Yang等人(2021)提出了一种SPA(stochastic probability adjustment)的无监督学习方法,SPA将SNN的突触和神经元映射到一个概率空间中,其中一个神经元和所有连接的突触前都由一个簇表示。突触在不同簇之间的运动建模为一个类似布朗的随机过程,其中发射器的分布在不同的放电阶段是自适应的,通过随机过程的约束,减少了SNN的整体竞争,提高分类精度。
无监督的学习算法更加接近于实际生物性原理,利用生物神经元和突触的动力学原理进行训练,利用局部优化的方法更新突触权重,是更加类脑的方法,但是这种训练方法也存在一些缺点,无法构建深层次的复杂神经网络,因此借鉴于ANN易于计算的优点,出现了一些利用ANN反向传播的训练和ANN转换SNN等算法,这些方法融入了一些ANN思想,更加容易计算,也更易于训练大规模复杂结构的神经网络。
4 脉冲神经网络的监督学习算法
人在学习的过程中也存在反馈机制,这里的监督学习算法主要是利用输出值和目标值的误差来调整网络的连接权值,这种方法结合了ANN易于训练和SNN生物可解释性的优势,按照具体的训练方法将SNN的监督学习算法分为基于梯度下降、基于突触可塑性、基于ANN2SNN转换以及基于卷积的学习方法4种,其中ANN2SNN转换的学习算法属于间接训练方法。近年来,根据SNN的特性,也涌现出很多SNN的有监督学习算法,在图像识别领域得到广泛应用。
4.1 梯度下降的学习算法
SNN的基于梯度下降的监督学习算法的主要思想与ANN的梯度下降优化算法类似,利用输出脉冲序列与目标脉冲序列之间的误差,优化更新突触连接的权值,该方法的主要困难是离散脉冲不可微的性质,因此根据脉冲的特性很多适用于脉冲的误差反向传播方法也陆续提出。脉冲发放的频率及时间中存在的信息,利用梯度替代法或者脉冲发放的相对时间等方法,进行误差的反向传播以更新权值。
Bohte等人(2002)的SpikeProp算法是最早提出的一种经典的基于梯度的SNN学习算法,其思想与ANN的误差反向传播类似。SpikeProp用的是SRM神经元模型,该算法限制每个神经元只发放一次脉冲,采用时间编码的方式,提出了一种多层的前馈SNN的梯度下降学习算法。根据梯度反向传播原理,假设了一个阈值函数xj(t)与脉冲发放的时刻t在其最小邻域附近存在一个线性关系来进行突触的权重更新。
Gütig和Sompolinsky (2006)提出的Tempotron算法是一种生物可解释的有监督的突触学习规则,其认为神经元脉冲的信息不只是脉冲发放频率,而存在于脉冲序列的时空结构中。Tempotron算法用的是LIF神经元模型,脉冲神经元接收突触前神经元的所有输入脉冲的加权和,如果其突触后神经元的膜电位上升超过阈值,则会发放脉冲,在二分类任务中,对于应该发放脉冲的模式而没有发放脉冲就会增强突触连接,对于应该不发放脉冲的模式而发放了脉冲则会抑制突触连接,根据这样的规则来更新突触连接的权重。
由于Tempotron算法的输出神经元输出的脉冲时间是任意的,不携带信息,Florian(2012)提出了一种时间编码的算法chronotrons,包括有更高的存储性能的E-learning算法和有更高生物可解释性的I-learning算法,可以在发放时间上精确到亚毫秒级的脉冲序列,根据带有时间信息的脉冲序列来对不同的输入进行分类。
近年来,也涌现出各种新的误差反向传播的学习训练方法,利用误差反向传播思想,主要是根据脉冲的频率信息或者时间信息,得到权重更新的梯度进行训练。
Tempotron算法是单层的网络结构,特征提取能力可能不够强,而ANN中的卷积操作有更强的特征提取能力,Xu等人(2018)提出了一种结合卷积神经网络(convolutional neural network,CNN)特征提取能力的SNN模型CSNN(CNN-SNN),可以将CNN的特征学习能力和SNN的认知能力结合起来以更好地提取特征,CNN部分称为感知器,SNN部分称为认知器,首先用CNN的卷积操作来提取输入图像的特征,然后将特征用时间编码得到时空脉冲序列,输入到SNN认知器中,然后利用Tempotron学习规则训练,最后使用赢家通吃的分类策略。这种学习方法类似于人脑的神经节细胞和复杂细胞的特征提取功能,具有更强的特征提取能力。

Shrestha和Orchard(2018)提出了一种基于脉冲时序的误差反向传播策略SLAYER(spike layer error reassignment),克服了脉冲函数不可微的问题,而该方法用的是SRM神经元模型,SLAYER将采样时间Ts离散化,在一个周期中采样一定的样本,将脉冲的时序依赖表示到梯度,该方法用脉冲神经元状态变化的概率密度函数来表示脉冲函数的导数,以解决脉冲函数不可微的问题。由于脉冲神经元的状态取决于其输入神经元之前的状态,该方法不仅像传统方法一样反向传播了误差的信用度,还反向传播了时序的信用度,并且,用该方法训练了卷积和全连接的结构。
通过近似模拟反向传播优化全精度的梯度实现权值的算法需要很多浮点操作,而这在神经形态的电路中是不兼容的,因此Thiele等人(2019)提出了一种SpikeGrad反向传播训练方法。该方法将梯度离散化成脉冲事件进行反向传播,与前向传播离散化成脉冲序列一样,将误差离散化成脉冲序列从最后一层向前传播更新权重,并且证明了此方法可以实现与ANN等效的网络结构。
一般SNN的误差反向传播可以分成两种方法,一种是适合于脉冲神经网络的计算梯度的方法;另一种是根据脉冲发放的相对时间来传播误差。第1种方法的思想与ANN中的梯度下降优化算法相似,很多研究都是基于这种方法,STBP和SLAYER都属于这种方法。Lee等人(2020)提出了一种近似导数方法来描述LIF脉冲神经元模型的激活函数,类似于ANN中的激活函数可以使得梯度下降优化,整个过程包括前向传播、反向传播和权值更新。前向传播的最后一层不发放脉冲,只累积膜电位,再利用链式法则分别求得最后一层和隐藏层的梯度,然后更新连接的权值。
由于其他的BP(back propagation)算法要利用时空信息进行反向传播,使得计算规模和模型复杂度较高,Wu等人(2021)提出了一种基于累积脉冲流的反向传播算法ASF-BP(accumulated spiking flow), ASF-BP算法的权重更新不是依赖于输出脉冲神经元的脉冲序列更新的,而是让输出神经元设置一个很高的阈值,让其不发放脉冲,而在一个时间窗口内,累积计算输出层的脉冲流,累积脉冲流是脉冲神经元在时间窗口的累积输入和输出,损失函数计算累积脉冲输出流与实际标签的误差。ASF-BP算法计算累积脉冲输出流,显著降低了计算复杂度。
在ANN的训练中有利用弱分类器集成一个强分类器的框架,这样虽然每个分类器表现未必很好,但是集成模型会有较高的准确率,因此Shen等人(2021)根据这种思路,提出一个HybirdSNN模型,将多个浅层的SNN集成为一个强分类器,通过数据驱动的贪婪优化算法来有效组合浅层的SNN,这样在能耗和性能上更有优势,提出了3种模型组合的方法:利用Tempotron规则的T-HybirdSNN、利用Mostafa算法的M-HybirdSNN和利用监督BP的C-HybirdSNN。这种框架没有固定的深度结构,更加灵活,可以适应更多样化的任务。
利用替代梯度方法会存在一定的误差,Deng等人(2022)分析了利用梯度替代直接训练产生损失的原因,并提出了TET(temporal efficient training)方法来补偿梯度下降时使用替代梯度法导致的损失,TET不是直接优化积分电位,而是优化每个时刻的突触前输入,避免了陷入局部最优,网络也更具有鲁棒性。
第2种方法利用脉冲发放的相对时间来计算梯度,脉冲发放的时间顺序中也会隐含很多信息,Comsa等人(2020)提出了一种编码脉冲的相对时间的学习算法,并且使用有突触传递的alpha函数的SRM模型,输出层根据第1个发放脉冲的神经元来分类,其学习目标是使得脉冲发放的相对时间顺序是正确的。
Comsa等人(2020)的方法是一种延迟学习的方法,脉冲发放时间定义为膜电位的函数,脉冲的延迟或者顺序中隐含了信息,Kheradpisheh和Masquelier(2020)提出了一种使用更简单的脉冲神经元LIF模型的方法,该方法使用了一种时间编码rank-order-coding,所有神经元都只发放一个脉冲,根据脉冲发放的顺序信息来训练网络。基于这种网络提出一种新的学习方法S4NN(single-spike supervised spiking neural network),将输入数据转换成脉冲序列,用IF神经元来处理输入脉冲,根据第1个发放脉冲的神经元判断类别,然后将误差方向传播训练权重。
Zhang和Li (2021)提出脉冲时间序列的反向传播学习算法TSSL-BP(temporal spike sequence learning backpropagation),通过调整的LIF神经元前向传播脉冲序列,根据目标序列和输出序列的误差,反向传播更新权值,这种方法打破了神经元之间和神经元内的依赖,通过突触前发放脉冲的特征来捕获神经元内依赖性;它考虑每个神经元状态随时间的内部演化,捕捉同一突触前神经元在不同的脉冲时刻如何影响其突触后神经元。
两种SNN的误差反向传播的方法都存在一定的局限性,Kim等人(2020)提出一种基于激活值和基于时间的脉冲网络学习算法ANTLR(activation-and timing-based learning rule)将两种方法结合起来,可以像基于时间的方法改变脉冲时间且像基于激活值的方法移除脉冲。ANTLR用的是LIF模型,研究了基于激活值的方法和基于时间的方法之间的联系,发现当单个脉冲状态变化时两个方法是互补的。ANTLR的主要思想是将基于激活值的梯度和基于时间的梯度相加,得到一个联合梯度,并通过对二者设置系数来平衡二者的重要程度。
通过类似于ANN梯度下降优化的思想来训练SNN,主要是根据脉冲神经元的动力学特性,得到对于脉冲的梯度,进而更新连接权值,其中最主要的困难在于脉冲二值性的不可微特性以及神经元复杂的动力学原理。但是近年出现很多根据神经元动力学特征求梯度进而更新权值的方法,这种方法使得SNN不仅具有生物学特性且易于优化计算,可以在大规模复杂网络结构中应用。
4.2 ANN2SNN的学习算法
ANN2SNN学习算法是一种间接的学习算法,因为直接训练SNN在梯度传播上存在困难,因而将梯度传播的过程转移到ANN上,在ANN的网络中训练更新权值,再将权值转移到SNN上进行优化,这样避免了直接在SNN上计算梯度,让SNN可以应用于一些大规模复杂神经网络。
考虑到SNN脉冲的二值性难以直接训练,Cao等人(2015)提出了一种将深度人工卷积神经网络CNN转换为SNN的框架,这样可以将在ANN中训练好的权值转移到SNN中以间接地训练SNN,其中提到ANN转换为SNN导致精度损失的3个主要原因:1)负数输出值在SNN中很难表示;2)SNN很难表示ANN中的偏置项;3)需要用两层来表示ANN中的最大池化层而增加了计算复杂性。
Cao等人(2015)针对这3个问题提出了解决办法,首先用ReLU激活函数避免了负值的出现;去掉了卷积层和全连接层的偏置项;用空间线性采样代替最大池化。论文中的方法包括3个卷积操作和线性空间采样操作,首先将RGB图像通过编码生成脉冲,在SNN中用的是LIF神经元模型,最后由全连接层输出计算脉冲的数量。
用ANN中的神经元脉冲发放频率来模拟ANN中的激活值是ANN-SNN的主要方法。近年来也有人基于此提出了各种学习方法,Rueckauer等人(2017)提出了一种将常见的CNN的操作如最大池化、softmax和批归一化等转换到SNN中的方法,使得可以将任意网络转换成SNN。ANN中常有的偏置项在SNN中通常难以表示,提出用一个恒定的输入电流来表示偏置项。在ANN中通常有批归一化层来使得特征输入保持为正态分布便于特征提取,Diehl等人(2015)提出了两种权重归一化的方法:model-based normalization和data-based normalizationo。model-based normalization通过计算最大的可能激活值作为缩放因子缩放权重的值;data-based normalization将激活值和权重的最大值作为缩放因子,在data-based normalization的基础上将偏置考虑进去。Cao等人(2015)利用泊松分布来将像素值转换为脉冲,但是这种转化会损失网络的精度,因此将输入的激活值作为恒等的电流,将恒定的电荷值在每个时间步长添加到膜电位,先前的ANN2SNN只是用脉冲的最大输出个数来分类,没有转换softmax层,该文通过计算累积的膜电位来进行分类。在Cao等人(2015)的研究中,是用平均池化代替的最大池化层,而在该文中提出了一个门控单元让放电最大的神经元的脉冲通过来实现最大池化操作。
Sengupta等人(2019)提出了一种spike-norm用于ANN2SNN的批归一化层方法,与Diehl等人(2015)的归一化方法不同,每层的权重归一化根据spike的输入来确定。可以将神经元的阈值设为1,用缩放因子调整权重使得权重归一化;也可以将阈值设为最大激活值而权重不变达到阈值平衡。不仅实现了VGG结构网络的ANN2SNN转换,还扩展到残差网络结构上。
Sengupta等人(2019)的转换方法使用的是硬重置。Han等人(2020)研究发现,从ANN转换到SNN的精度损失大多来自于神经元的阈值硬重置,因此提出了基于软重置的ANN-SNN的方法RMP(residual membrance potential)脉冲神经元,保留了脉冲神经元在发放脉冲瞬间的膜电位,RMP-SNN通过将发放脉冲时的膜电位减去阈值,而不是重置到固定电位,使得在发放脉冲的瞬间保留了残余电位,从而减少了ANN-SNN转换过程中的信息损失。
为了更好地让脉冲发放速率近似ANN网络中的激活值,Ding等人(2021)提出了一种ANN2SNN的优化算法,该算法提出一个RNL(rate norm layer)层来代替ANN中的ReLU层,研究发现使用阈值或者权重归一化的方法需要有缩放操作,而比例因子需要人为选择,该算法的RNL层是一个带有可训练上限的clip函数,并且该算法还提出了一个拟合曲线来量化ANN的模拟脉冲频率和SNN实际脉冲频率,这减少了训练的延迟。
Deng和Gu(2021)提出了一种新的策略管道将阈值平衡和软重置机制结合起来的ANN-SNN转换方法,这种管道使得ANN和转换后的SNN之间几乎没有精度损失,从理论上分析了转换过程,总体误差可以转换成各层的误差,修改了ReLU激活函数以近似SNN的脉冲发放频率,控制每一层的ANN的激活值和目标SNN之差,根据Diehl等人(2015)和Sengupta等人(2019)的阈值平衡机制估计每一层的最优位移值并计算总体转换误差。
为了让转换后的SNN的参数更加匹配ANN的激活值,Li等人(2021)提出了一种SNN校准的方法,分析了从ANN转换到SNN的误差,并提出了分层修正误差的算法,认为转换误差通常来自两个方面:flooring误差和clipping误差,提高阈值会降低clipping误差提高flooring误差。为了平衡这两种误差,用MMSE(mean squared error)来得到合适的阈值。该方法还校准了SNN的参数来减少误差,包括权重和偏置项。
ANN-SNN的方法需要较多的时间步长,但是这样会有较大的时间延迟,Bu等人(2022)提出了一种具有低延迟的高性能算法,时间步长小于32,通过优化初始膜电位来减少误差,发现将膜电位初始化为阈值的一半时转换误差的期望可以达到最小值。
利用神经元的脉冲频率编码来进行ANN-SNN的转换会有较大的时间延迟,训练收敛的时间比较长,Han和Roy(2020)提出了一种基于时间编码TSC(temporal-switch-coding)的ANN-to-SNN的转换方法,每个输入图像的像素用两个脉冲来表示并且这两个脉冲之间的时间与像素强度成正比,这种编码方式比TTFS(time-to-first-spike)能耗更低,每次激活最多只需要发放两个脉冲,仅在输入脉冲时跟踪突触,减少了计算成本。
ANN-SNN的学习算法让SNN直接获得ANN中训练好的权重,而ANN-SNN的学习算法有较大的延迟,基于梯度的算法虽然可以直接训练,但是其训练复杂度较高,所以Rathi等人(2020)提出了一种混合的训练方法,首先用训练好的ANN的权重,作为SNN初始权重,然后利用基于脉冲相对时间的梯度方向传播再训练SNN,这样减少了收敛的时间。
ANN-SNN的学习算法可以直接把训练好的权重转移到SNN中,可以构建较深层的复杂网络结构,让SNN的训练更加容易,但是这种方法会产生较大延迟,需要较多的时间步长才可以有较好的效果。
4.3 突触可塑性的学习算法
STDP是一种无监督的学习算法,通过突触可塑性原理来调整突触连接的权值,而相较于基于梯度的学习算法,基于突触可塑性的无监督学习算法难以扩展到深层复杂网络结构中,因而提出了结合监督学习思想的突触可塑性算法,Ponulak和Kasiński (2010)结合STDP和anti-STDP算法,提出了一种监督学习ReSuMe(remote supervised method)学习算法,ReSuMe算法根据突触前神经元和突触后神经元脉冲发放的时间来进行训练学习,类似于Widrow-Hoff规则,ReSuMe算法不是基于传统的梯度的优化算法,它利用突触可塑性原理最小化目标脉冲序列和输出脉冲序列之间的误差。对于兴奋性突触,让对发放脉冲的神经元有贡献的突触增强,遵守STDP规则;对于抑制性突触,让阻止神经元发放脉冲的突触抑制,遵守anti-STDP规则。
Taherkhani等人(2015)提出了DL-ReSuMe(delay learning remote supervised method)算法,由于突触的延迟不是固定的,DL-ReSuMe算法同时学习突触的权重和权值,更具有生物可解释性。在DL-ReSuMe的基础上又提出了Multi-DL-ReSuMe(multiple DL-ReSuMe)算法,可以训练多个脉冲神经元的分类任务,每个神经元可以识别一个类。
Wade等人(2010)将BCM(Bienenstock-Cooper-Munro)和STDP算法结合提出了SWAT(a synaptic weight association training algorithm)算法,SWAT产生一个单峰权重分布,与STDP有关的可塑性窗口高度被调制趋于稳定。SNN在隐藏层使用一个前馈循环拓扑结构,包括兴奋性和抑制性突触,利用STDP规则学习所有输出神经元的权重,再将权重映射到相对应的输出神经元。
梯度下降算法具有网络优化计算上的优点,而STDP规则具有生物可解释性的优点,为了将这两种优点结合起来,Tavanaei 和 Maida(2019)提出了一种基于时间突触可塑性的监督学习算法(BP-STDP),用STDP规则和anti-STDP规则的时间局部学习方法作为突触更新的规则,用教师信号选择STDP规则或者anti-STDP规则,并且可以应用到每个时间步。
Tavanaei 和 Maida(2019)的算法只利用了局部更新的规则,Liu等人(2021)提出了一种结合BP全局优化规则和时间局部更新机制的SNN学习算法,称为SSTDP(supervised spike timing dependent plasticity),前向传播时脉冲神经元接收到突触前神经元的加权膜电位,反向传播时根据链式法则更新权值,权值更新信息包括空间信息,即从STDP的局部权值更新,以及时间信息,即从BP的全局权值更新。
将突触可塑性原理和监督学习思想结合起来,利用STDP的规则来更新突触的权值,又加入了输出和目标的误差的优化算法。这样的算法更具有生物可解释性,且算法的训练更加容易。
4.4 脉冲序列卷积的学习算法
基于脉冲序列卷积的学习算法是利用卷积的思想,通过引入核函数,对离散的脉冲序列进行卷积,进而对脉冲序列,利用Widrow-Hoff规则调整突触权重进行训练。
Mohemmed等人(2012)提出了一种SPAN (spike pattern association neuron) 算法,在训练时将脉冲序列转换成模拟信号,可以应用普通的数学操作,用一个核函数κ(t)对每个脉冲序列进行卷积,通过这样的转换可以将Widrow-Hoff规则用于转换后的脉冲序列以调整突触权重
Yu等人(2013)提出了PSD(precise-spike-driven synaptic plasticity)学习算法,根据Widrow-Hoff规则,根据输出脉冲序列和实际脉冲序列的误差来更新突触权重,正的误差导致长时程增强,负的误差导致长时程抑制,PSD算法同时具有符合算数规则和生物可解释性的优点。与SAPN不同的是,PSD只对输入脉冲序列进行卷积,突触权重的调整由输出和实际脉冲的误差触发,只取决于当前的状态。
5 深度脉冲神经网络
近年来有相关研究探索SNN在深度学习中的应用,提出了很多将SNN用到深度学习网络架构中的方法,将浅层的SNN扩展到更深层的网络中,解决退化问题以及梯度问题,表现出较好的性能。
Hu等人(2021a)提出了一种S-Resnet模型(spiking ResNet),这是一种ANN-SNN的算法,该算法的网络结构是SNN,深度首次超过40层。S-Resnet用补偿机制减小从ANN到SNN转到导致的误差。用IF脉冲神经元替代ReLU激活函数,将训练好的Resnet模型转换到SNN,而由于脉冲的离散二值性质,转换的时候会产生一个误差,误差会随着层数的加深而逐渐累积,为了抵消误差导致的精度下降,提出将权重乘以一个缩放因子,稍微增大脉冲发放率抵消误差。该算法可以用于18,34,50层的残差网络结构中,且在大型数据集ImageNet上进行了测试。
Stöckl和Maass(2021)提出了用两个脉冲实现的高精度分类方法,FS(few spikes)转换是一种ANN转换SNN的方法,可以用于ResNet-50结构中,这个方法不同于频率编码的方法,而是利用脉冲时间模式中的信息,该文提出了一种少脉冲的神经元模型FS神经元模型,其内部动力学可以用少量的脉冲模拟ANN神经元。
SNN在反向传播的时候,脉冲特征不仅体现在空间上,还体现在时间上,而一般的BN(batch normalization)算法不适用于脉冲神经元,因此Zheng等人(2021)在STBP方法的基础上,提出了STBP-tdBN的方法,先前的研究中网络结构大多不超过10层,该方法可以避免梯度消失或者梯度爆炸,使得该方法可以应用到18、34和50层的残差网络中。tdBN(a threshold-dependent batch normalization)是一种脉冲归一化的方法,如图8所示,该方法对脉冲输入沿着通道这一维度进行归一化,不仅对空间还对时间上的脉冲进行了归一化。
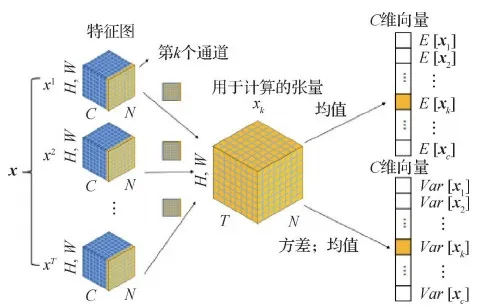
图8 tdBN的归一化方法示意图(Zheng等,2021)
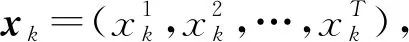
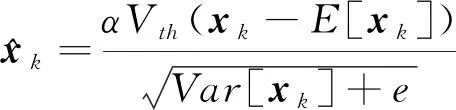
(10)
式中,e为阈值。
实验表明,该方法在深度的SNN上表现较好,且可以用于复杂数据集,如ImageNet。
Hu等人(2021b)在TDBN的基础上,调整了残差块的基本结构,删除了基础块之间的连接处的LIF神经元,将LIF神经元放在了残差路径的最上面,提出了MS-ResNet(the membrance-shortcut ResNet)。这样的结构使得在恒等路径中传递是膜电位而不是脉冲流,避免了无效的残差表达式,不会有梯度爆炸或消失的问题,该方法可以用在ResNet-104中。
残差网络的提出解决了ANN深层网络训练过程中的梯度消失或爆炸的问题,因而考虑将这种结构应用到SNN中,但是以往的spiking ResNet只是简单地将ReLU替换成脉冲神经元,没有考虑到脉冲神经元的特性,因而并不能完全实现残差网络的恒等映射,随着网络层数的加深仍然会存在退化问题,并且存在梯度消失和梯度爆炸的现象。因此,Fang等人(2022)提出了一种SEW(spike-element-wise) ResNet方法,这是第1次直接训练超过100层网络结构的SNN。根据脉冲神经元的特性,改进了SNN学习的残差网络,将基础残差块之间的激活函数层去掉,改用逐元素操作函数g(g=AND/IAND/ADD),实现了脉冲残差网络的恒等映射,解决了梯度爆炸或消失的问题。该方法可以用于34、50、101层的残差网络,实现了深度SNN的学习。
SNN在深度学习中也涌现出许多算法,大多利用反向传播的思想或者ANN转换SNN的方法,借鉴ANN中的一些深层网络结构,然后根据SNN脉冲的时间和空间特性提出适用于SNN的网络结构,而SNN在深层结构中也表现出不逊于ANN的性能。
6 总结与展望
图9总结了脉冲神经网络算法从出现到一些经典算法研究的进展,从最初的根据突触学习的生物性原理的单层网络,到借鉴了误差反向传播思想的直接训练和ANN2SNN的转换学习算法,近年来更有利用深度学习的复杂网络结构的脉冲神经网络。脉冲神经网络由于其独特的仿生特性,利用脉冲来传递信息,当膜电位超过阈值就会发放一个脉冲,这与生物细胞的动作电位类似,正是因为这种生物特性,其训练过程会有一定困难。目前的训练算法主要分为无监督学习、监督学习以及ANN-SNN转换的学习算法。其中,无监督学习主要利用了突触可塑性原理,这种算法生物可解释性很强,利用局部规则调整权重参数,但是这种方式无法用于复杂结构的网络模型;监督学习算法主要借鉴了人工神经网络的思想,将误差反向传播结合到脉冲神经网络的训练中,这种方法的主要困难是脉冲的不可微性,但是这种方法不仅具有生物可解释性的优点,也具有人工神经网络易于计算的优点,可以用于复杂网络结构;ANN-SNN的转换学习算法是将在ANN中训练好的权值转移到SNN上,这种方法主要利用了ANN训练的优势,可以用于像ANN一样的复杂网络结构,但是要达到相对较高的精度,需要较长的时间步长。脉冲神经网络作为第3代人工神经网络,未来将是类脑智能的核心,下面是对脉冲神经网络未来发展的展望:

图9 脉冲神经网络算法进展图
1)更加仿生的学习算法。未来可能会根据实际生物神经网络中突触连接的建立以及突触的增强和减弱的规则来构建脉冲神经网络,从生物神经网络的学习规则启发脉冲神经网络的学习规则,借鉴生物的视觉系统结构,构建更加仿生的模型。
2)更加复杂的、大规模的网络结构。未来可能会将脉冲神经网络应用于深度学习中,在网络结构上有所创新,将人工神经网络的算法思想与生物仿生模型结合,发挥二者的优势,构建深层次大规模的网络结构。
3)更加多样化的应用。未来类脑智能将是一个发展趋势,而更加仿生、更加高效的学习算法成为必需,探索生物脑的结构,构建更加强大的计算系统。
7 结 语
本文总结了脉冲神经网络中常用的脉冲神经元模型,概括了监督学习以及无监督学习的相关研究算法。监督学习方法主要利用反向传播的方法,通过输出层的误差来更新权值;无监督学习方法主要利用突触的生物性原理,根据脉冲发放的时序特性来更新权值。脉冲神经网络作为第3代的神经网络,由于其在生物学上的可解释性,更加近似于实际生物的神经元机制,随着研究的深入,也对脉冲神经网络的训练方法逐渐改进,其精度和性能也不断提高,为机器学习和深度学习提供一种新的范式。未来随着对人脑工作机制的探索,相信会出现更加仿生的、更加高效的脉冲神经网络学习算法,将结合数学模型计算的优势以及生物神经网络的工作原理,构建更加适合脉冲神经网络的训练方法,以在更多的实际领域得到应用。
