基于采煤机摇臂销轴载荷数据卡尔曼最优估计的煤岩识别方法

史光亮，尉瑞，王海燕，葛津铭，张盛涛

（1.中煤华晋集团有限公司，山西 太原 030002；2.辽宁工程技术大学 机械工程学院，辽宁 阜新 123000）

0 引言

采煤机是井下综采工作面主要机械设备之一，煤岩识别是采煤机进行自动截割控制的依据，是实现采煤机智能控制、提高煤炭开采效率及延长采煤机使用寿命的关键技术[1]。目前，大多数煤岩识别依靠人工主观判断，导致识别结果不准确且安全隐患突出。因此，实现采煤机对截割不同煤岩状态的准确判别是当前研究工作的重点与难点[2-3]。

目前，许多学者对煤岩识别技术进行了研究。王昕[4]分析了多频段电磁波煤岩识别技术，搭建了基于煤岩识别的电磁波模型，验证了基于电磁波的煤岩识别技术的正确性，为煤岩识别提供了新方法。王海舰[5]通过分析各截割信号的模糊性特征，建立基于最小模糊熵的隶属度函数优化模型，采用煤岩界面多信息融合决策识别模型显著提高了煤岩识别精度。文立堃[6]提出了试切滚筒进行煤岩识别的方法，通过截割信号的经验模态分解，得到趋势项中变异系数小的信号其趋势项更稳定。杨文萃等[7]根据声波传递到煤岩界面时存在反射与折射现象的特性，构建了计算煤层厚度的理论模型，并通过Simulink 进行仿真。J.Asfahani 等[8]利用具有低活性光谱的γ 射线，提出了采煤机滚筒截割工况的识别方法。孙继平等[9]针对煤炭开采与加工过程中采煤机滚筒高度调节、选煤厂预排矸等工程实际问题，提出了一种基于双树复小波域统计建模的煤岩识别方法，通过双树复小波变换对煤岩图像进行多级分解，引入旋转不变增强策略，采用基于尺度独立形状估计方程的广义伽玛分布参数估计方法确定模型参数，根据相对熵相似性测度完成煤岩图像的自动识别，该方法增强了煤岩之间的区别，具有较高的识别准确性。Zhang Dan 等[10]对煤岩切割过程中低频重建信号和不同硬度振动信号的功率谱进行了仿真，证明了通过与凿岩机接触可实现对煤岩的识别，为井下螺杆采煤机的智能控制奠定了基础。刘俊利等[11]提出了一种采用振动传感器进行煤岩识别的方法，通过截割不同硬度材料，获取采煤机摇臂上的振动信号，根据振动信号傅里叶变换后的幅值差异，识别煤岩介质。Wang Xin 等[12]对多种煤岩在太赫兹波段的吸收系数、光谱、折射率和介电性质等物理性质展开研究，采用主成分分析和支持向量机等方法准确识别煤岩。薛光辉等[13]对放顶煤的声压数据时域特征进行分析，发现方差对煤岩性状具有更高的识别率。张强等[14]提取主动红外激励下煤岩的温度场信息，建立温度梯度模型，从而识别煤岩界面。王海舰等[15]考虑截齿处于不同程度磨损的状态，采集电流、振动及声发射等信号，构建D-S 理论的决策准则，实现煤岩界面的精准识别。现有研究方法对现场环境及检测设备要求较高，实际综采工作面难以满足研究所需的必要条件。在不增加外部附属仪器设备的基础上，采用采煤机摇臂销轴传感器替换现有销轴感知煤岩载荷，可较好地适应环境。因此，本文提出了一种基于采煤机摇臂销轴载荷数据卡尔曼最优估计的煤岩识别方法。采用卡尔曼最优估计算法对载荷数据进行降噪处理，使采煤机在截割煤岩等不同工况下的载荷区间相互分开，通过判断实时载荷处于的区间实现煤岩识别。

1 摇臂销轴力学特性分析

采煤机由滚筒、摇臂、摇臂销轴、连接架、牵引部等组成，其结构如图1 所示。摇臂销轴是采煤机摇臂与机身连接的重要部件，截割煤岩时滚筒所受负载经过摇臂壳体作用在摇臂销轴上。因此，在截割煤岩时对摇臂销轴受力进行分析。

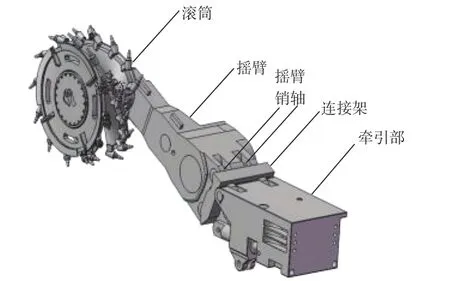
图1 采煤机结构Fig.1 Shearer structure

摇臂销轴空间受力模型如图2 所示，其中，o-xyz为大地坐标系，（x1，y1），（x2，y2），（x3，y3），（x4，y4）分别为每根销轴的坐标。摇臂销轴受力来自滚筒截割的三向力与摇臂、滚筒及传动齿轮组的自身重力，通过摇臂与连接架连接的4 根销轴，每根销轴分解成2 个方向的力Fx,Fy，摇臂对摇臂销轴共有8 个作用力，它们互为作用力与反作用力。其中，滚筒三向（X，Y，Z）载荷为FX，FY，FZ，煤壁侧摇臂上下销轴受力分别为Fx1，Fy1，Fz1，Fx3，Fy3，Fz3，采空侧摇臂上下销轴受力分别为Fx2，Fy2，Fz2，Fx4，Fy4，Fz4，各个受力力臂分别为l1-l6，摇臂与水平方向夹角为α。

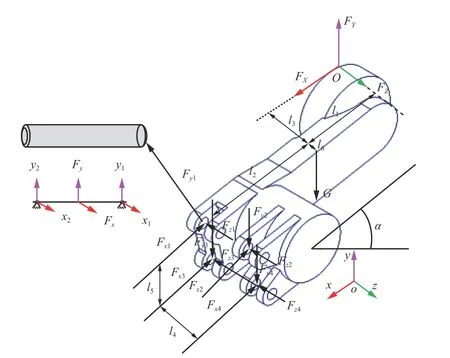
图2 摇臂销轴空间受力模型Fig.2 The spatial force model of rocker arm pin axle

以摇臂滚筒中心为坐标轴O点，基于摇臂销轴的受力平衡方程为

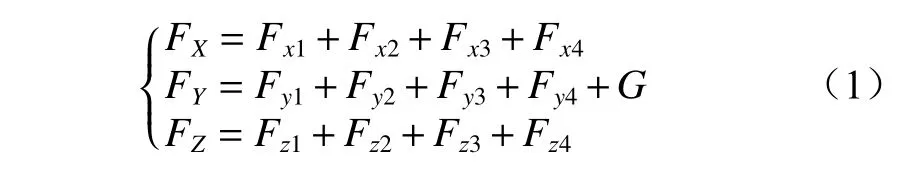
对O点的力矩平衡方程[16]为

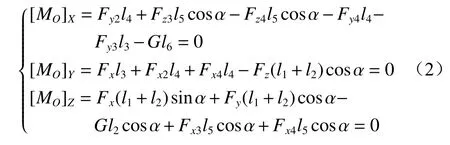
式中：G为摇臂重力；[MO]X，[MO]Y，[MO]Z分别为X，Y，Z方向的中心力矩。

滚筒截割煤岩时受到的作用力与摇臂销轴受力成正比，即滚筒受力越大，作用在摇臂销轴上的载荷越大。

2 卡尔曼最优估计算法

2.1 算法原理

卡尔曼滤波是纯时域的滤波器，不需要进行频域变换，卡尔曼算法是一种通过递推实现从测量值中估计真值的方法[17]，分为状态更新和时间更新2 个部分，如图3 所示。根据传感器测量值的变化量，再根据经验给出过程噪声与测量噪声，进行时间与状态更新[18]，即可达到降噪效果。

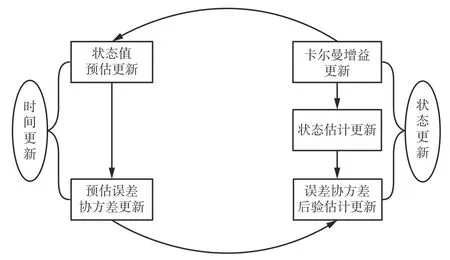
图3 卡尔曼算法流程Fig.3 The Kalman's algorithm flow

2.2 卡尔曼算法模型

设随机离散系统的方程为

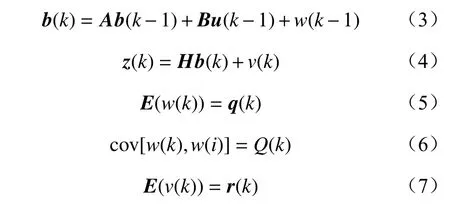
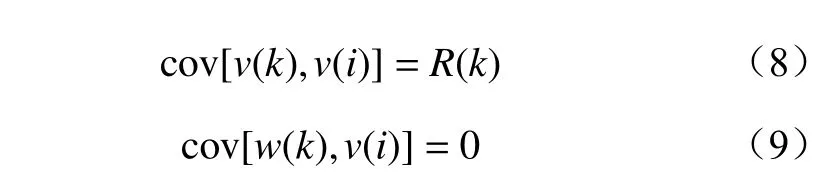
式中：b（k）为k时刻的n维系统状态向量；A为n×n阶系统转移矩阵；B为n×L阶控制输入增益矩阵；u（k-1）为L维控制输入向量；w（k），w（i）分别为系统在k，i时刻的过程噪声；z（k）为系统在k时刻的测量向量；H为测量矩阵，用来表示状态向量对测量向量的增益，通常用来进行统计单位之间的转换，若单位统一，可取值为常数1；v（k），v（i）分别为k，i时刻的测量噪声；E（w（k））为误差向量；q（k）为距离；Q（k）为过程噪声的协方差，通常按照经验选取，本文根据观测值估计出协方差；r（k）为等效半径；R（k）为噪声协方差，通常按传感器精度选取，R（k）越大，最终的状态估计越信任预测值。

系统状态向量的预估为

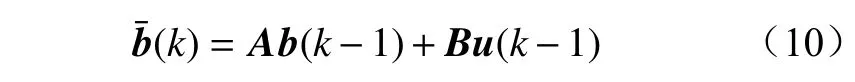
误差协方差预估为

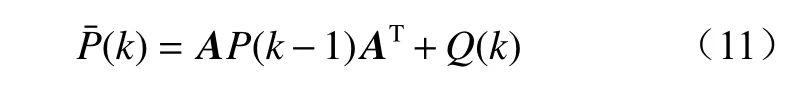
式中P（k-1）为k-1 时刻误差协方差后验估计，P（k-1）的初始值通常取1，在自适应过程中会自动调整。

卡尔曼增益为

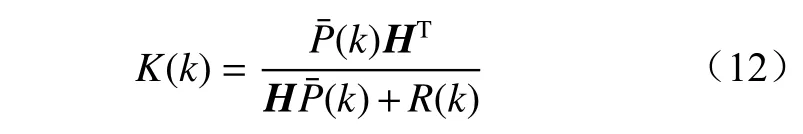
最终的系统状态向量为

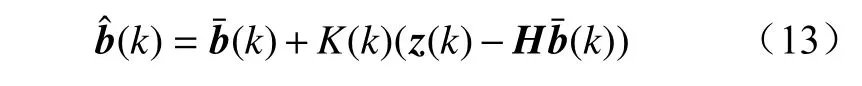
误差协方差根据误差协方差的后验估计进行实时更新。

式中I为单位向量。

2.3 仿真分析

为了验证卡尔曼最优估计算法对载荷信号降噪的可行性与优越性，构建随机载荷信号：

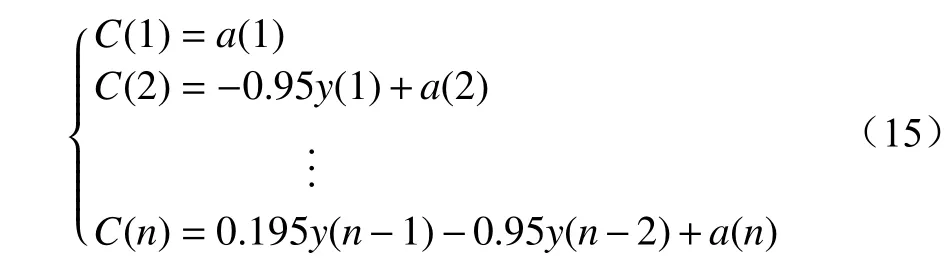
式中：C为随机信号；n∈[3,3 000]；a（n）为均值为0、标准差为1 的随机数。

利用卡尔曼最优估计算法、最小均方（Least Mean Square,LMS）自适应估计算法、变步长LMS 自适应估计算法对相同信号进行降噪处理，仿真信号曲线如图4 所示。可看出仿真数据呈周期变化。

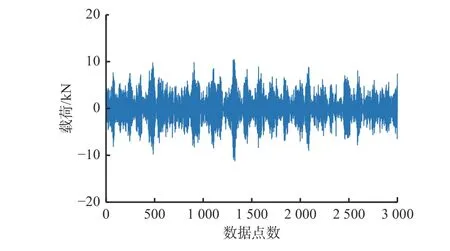
图4 仿真信号曲线Fig.4 Simulation signal curve

通过降噪处理后得到每种算法的均方误差曲线，如图5 所示。可看出LMS 自适应估计算法均方误差为0～0.296，变步长LMS 自适应估计算法均方误差为0～0.121，卡尔曼最优估计算法均方误差为0～0.003 16，说明经卡尔曼最优估计算法处理的仿真信号具有更小的均方误差，因此，卡尔曼最优估计算法具有更好的性能优势。

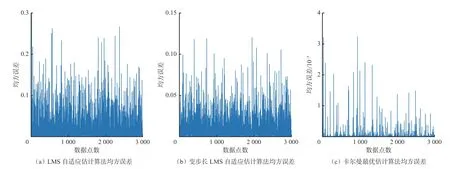
图5 多种降噪算法均方误差对比Fig.5 Comparison of mean square error of various noise reduction algorithms

3 煤岩识别实验

3.1 实验测试平台搭建

本次实验以张家口综采实验平台为依托，实验测试平台包括煤岩截割系统和信号采集系统。煤岩截割系统包括采煤机、刮板输送机、液压支架等综采成套设备和模拟的煤壁，如图6 所示。采煤机型号为MG500/1130-WD，其滚筒直径为1.8 m，总功率为1 130 kW，滚筒转速为28.5 r/min，截深为800 mm；实验中分别制作坚固性系数f=3 和f=4 的实验样件，由煤炭、水泥、沙子等粘合制作，采用等效替代的思想，f=3 模拟煤壁的实际条件，f=4 模拟岩石的实际条件。

图6 煤岩截割系统Fig.6 Coal and rock cutting system

信号采集系统由摇臂销轴传感器、无线通信转换器、无线采集模块、上位机和采集分析软件组成。摇臂销轴传感器与无线采集模块连接并将采集数据发送给上位机，上位机通过安装在上位机无线通信转换器接收数据，由采集分析软件处理数据。

摇臂销轴传感器是按照摇臂销轴结构尺寸定制的，对其进行等效强度处理后代替摇臂销轴安装在摇臂与连接架连接处，在连接架与摇臂销轴的铰接处布置应变测点，用应变变形量间接测量摇臂销轴2 个径向方向所承受的载荷，测点位置与承受载荷如图7 所示。销轴传感器现场安装如图8 所示。

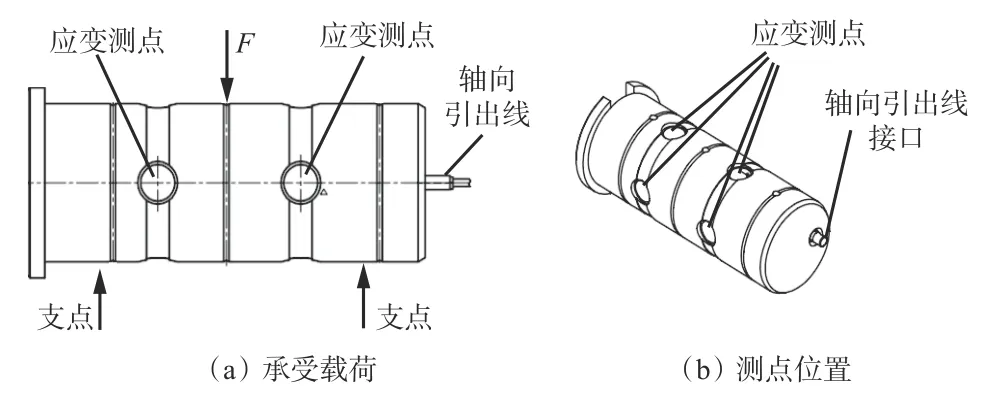
图7 测点位置与承受载荷Fig.7 Measurement point position and bearing load

图8 摇臂销轴传感器现场安装Fig.8 Field installation of rocker arm pin axle sensor

摇臂销轴传感器轴向引出线与无线采集模块相连，用以采集摇臂销轴传感器测点的应变信号，每秒采集200 个数据。无线采集模块将采集到的应变数据通过无线通信转换器传输到上位机中加以分析。数据采集和传输过程如图9 所示。

图9 数据采集及传输过程Fig.9 Data acquisition and transmission process

3.2 实验结果分析

对煤壁侧上端摇臂销轴沿采煤机牵引方向的载荷进行分析，开展煤岩识别实验。实验过程分为空载、截割煤壁（f=3）、截割岩石（f=4）3 个阶段。考虑到大部分岩性介质硬度大于煤层介质，所以将f=4 的煤壁作为岩壁介质进行分析。摇臂销轴传感器采集的是微应变，根据摇臂销轴传感器出厂加载标定实验，得到微应变与载荷之间的关系：

式中：S为实验得到的微应变，με；V1为供电电压，V1=1.5 V。

根据标定实验的关系方程和测量到的微应变，得到空载、截割煤壁、截割岩石时摇臂销轴载荷，如图10 所示，其中载荷的正负号代表受力方向。可看出在空载阶段，由于采煤机摇臂和滚筒自身重力与齿轮振动和行走摩擦作用，载荷信号在一定范围内无规则波动；在截割煤壁和截割岩石阶段载荷也在一定范围内无规则波动，但是波动范围远远大于空载阶段，即离散程度更大。空载、截割煤壁和截割岩石3 种工况下摇臂销轴载荷及均方差见表1。可看出在截割煤壁与截割岩石阶段，由于噪声及振动等原因，相应载荷区间存在重合部分，以此范围判别煤岩状态具有一定误差，所以在此基础上，对载荷真实值进行最优估计，以降低噪声等对状态判别的影响。

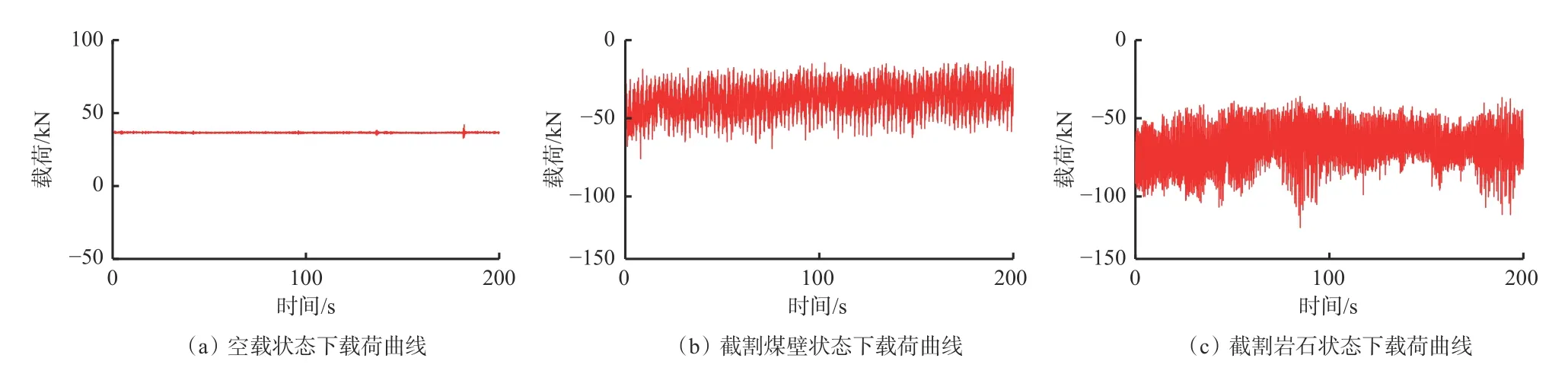
图10 空载、截割煤壁和截割岩石工况下摇臂销轴载荷曲线Fig.10 Load curve of rocker arm pin axle under no-load,cutting the coal wall and cutting the rock

空载、截割煤壁、截割岩石3 种工况下经过最优估计处理的摇臂销轴载荷曲线如图11 所示。可看出：空载阶段的数据在0～1.1 s 自适应收敛；截割煤壁阶段的数据在0～1.7 s 自适应收敛；截割岩石阶段的数据在0～2.6 s 自适应收敛。与未经最优估计处理之前的数据相比，经最优估计处理后的载荷数据曲线更加平稳，其波动范围明显减小，离散程度更小。本文实验中的实验样件模拟煤壁与岩石条件，截割煤壁载荷为-25～-50 kN，截割岩石载荷为-59～-75 kN，因此井下煤炭开采过程中遇到坚固性系数更高的岩石时，摇臂销轴处最终识别出的载荷变大，煤岩识别精度进一步提高。

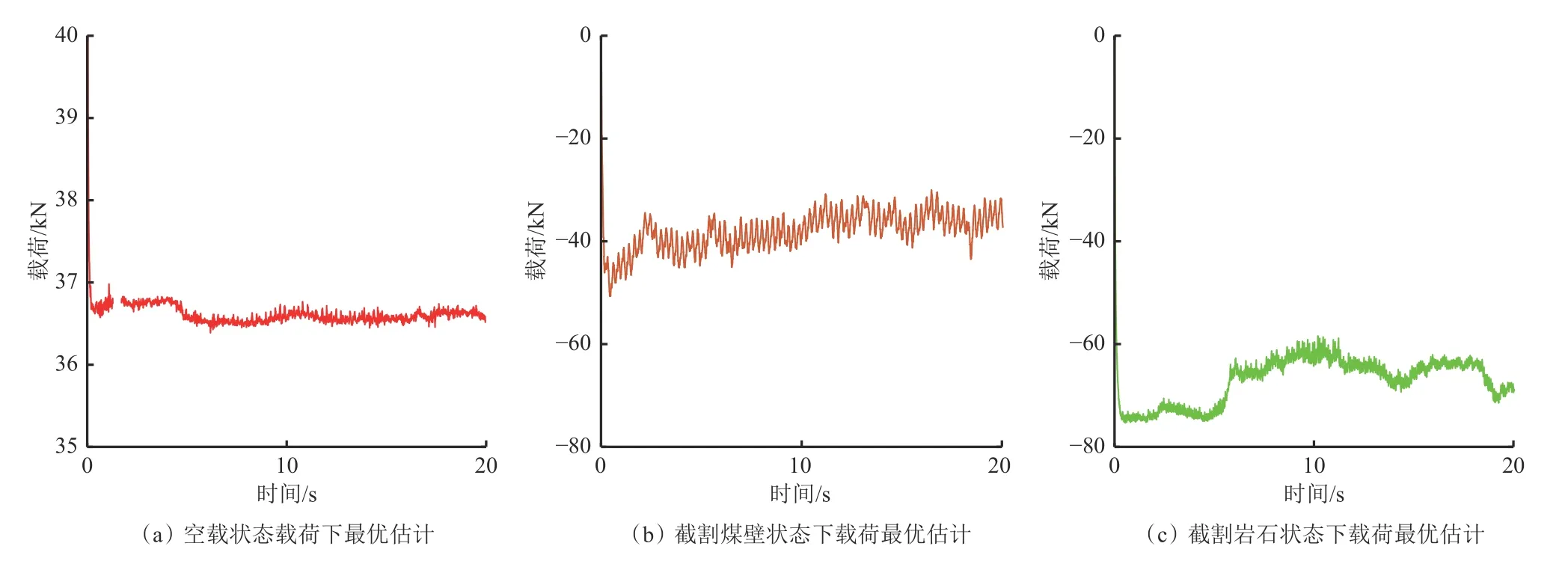
图11 空载、截割煤壁和截割岩石工况下摇臂销轴载荷最优估计Fig.11 Optimal estimation of rocker arm pin axle under no-load,cutting the coal wall and cutting the rock

经过最优估计处理的3 种工况下摇臂销轴载荷区间及均方差见表2。可看出与未经最优估计处理之前的数据相比，经最优估计处理后的载荷区间长度降低了65.6%～83.3%，均方差降低了66.5%～72.9%，数据波动更小，有效提高了数据的辨识度，各状态下载荷区间均不存在重叠。因此，可根据经过卡尔曼最优估计算法处理的载荷区间作为煤岩识别依据，在实际工程应用中设定截割煤层状态时的期望载荷受力范围，一旦超出该范围，则判断此时不是截割煤壁状态，达到煤岩识别的目的。

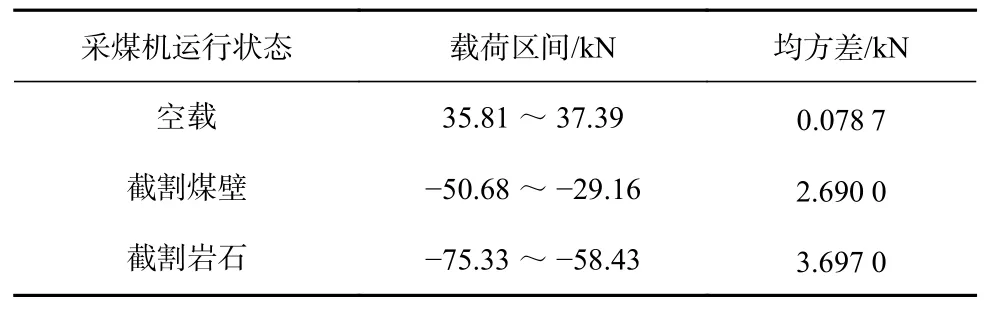
表2 最优估计处理后空载、截割煤壁和截割岩石工况下摇臂销轴载荷区间及均方差Table 2 Load interval and mean square difference in each state after optimal estimation

4 结论

（1）经过卡尔曼最优估计处理后，空载阶段的载荷数据在0～1.1 s 自适应收敛；截割煤壁阶段的载荷数据在0～1.7 s 自适应收敛；截割岩石阶段的载荷数据在0～2.6 s 自适应收敛。与未经最优估计处理之前的数据相比，载荷数据曲线更加平稳，波动范围明显减小，离散程度更小。

（2）采用卡尔曼最优估计算法对空载、截割煤壁和截割岩石工况下的载荷数据进行处理，相对于未处理之前，载荷数据区间长度降低了65.6%～83.3%，均方差降低了66.5%～72.9%，载荷参数辨识度得到提高，且每个工况下的载荷差异更加明显，对应的载荷范围均不存在重合部分，能够更精准确定每种工作状态，实现煤岩识别。

（3）将经过卡尔曼最优估计算法处理的载荷区间作为煤岩识别依据，在实际工程应用中设定截割煤层状态时期望载荷受力范围，一旦超出该范围，则判断此时不是截割煤壁状态，达到煤岩识别的目的。