悬臂式掘进机自主调速截割控制系统
2023-02-21张旭辉石硕杨红强杨文娟张超王甜
张旭辉,石硕,杨红强,杨文娟,张超,王甜
(1.西安科技大学 机械工程学院,陕西 西安 710054; 2.陕西省矿山机电装备智能监测重点实验室,陕西 西安 710054)
0 引言
“十四五”煤炭科技的发展目标是实现井下重点岗位机器人作业,大型煤机装备的智能化和可靠性水平大幅提升,控制系统与软件实现自主化[1-2]。在掘进工作面,煤矿井下光照强弱不均、高粉尘等增加了司机对掘进机截割臂控制的难度[3-4]。为了提高巷道断面自动成形质量,需要深入研究悬臂式掘进机智能截割控制[5-6],对于提高掘进工作面智能化水平具有重要意义[7]。
王苏彧等[8]探究了掘进机断面成形轨迹优化方法,采用基于知识库精简的多目标粒子群算法求得最优轨迹,但产生的曲折轨迹在实际运动中截割臂较难跟踪。田劼等[9]采用混合杂草优化(Invasive Weed Optimization,IWO)-粒子群优化(Particle Swarm Optimization,PSO)算法对掘进机截割轨迹进行优化,但是没有考虑负载情况下的断面成形精度。王旭启等[10]提出了一种基于模糊算法的掘进机截割机构变频控制策略,利用截割电动机电流对掘进机截割参数进行调整,但仅对控制策略进行了验证。谢亚洲[11]提出了一种悬臂式掘进机智能控制系统,该系统以DSP+CPLD 为核心,实现了掘进机自适应煤岩截割,但延时较大。谢苗等[12]提出了一种基于神经网络和PID 的智能调速系统,以压力为反馈对掘进机摆动速度进行调节,但安装在掘进机截齿上的压力传感器易损坏,难以应用于环境复杂的掘进工作面。毛清华等[13]提出了一种基于PID 控制的悬臂式掘进机截割头位置控制方法,但采用无调速的位置控制方法在长时间运行后控制精度较差。张旭辉等[14]提出了一种悬臂式掘进机视觉伺服截割控制系统,利用视觉测量系统反馈截割头位姿,实现巷道断面截割成形,但未考虑截割过程中的自主调速。
上述研究采用较为单一的控制方法且截割头以定速实现巷道断面截割,未综合考虑轨迹规划和自主调速控制,在复杂地质条件下较难提升井巷工程质量。因此,本文提出了一种悬臂式掘进机自主调速截割控制系统。通过分析截割头受到的反作用力和截割臂摆动速度之间的关系,对截割头加速度进行分层以获取目标截割臂摆动速度;利用运动学逆解计算截割头到达离散截割轨迹规划点所需的控制量,并采用模糊PID 控制驱动截割头变速截割煤壁,从而提高巷道断面成形质量。
1 总体方案
悬臂式掘进机自主调速截割控制系统由MV-EMV510 后置工业相机、MV-EMV130 前置工业相机、激光指向仪、工控机、加速度传感器和红外LED 标靶组成,如图1 所示。
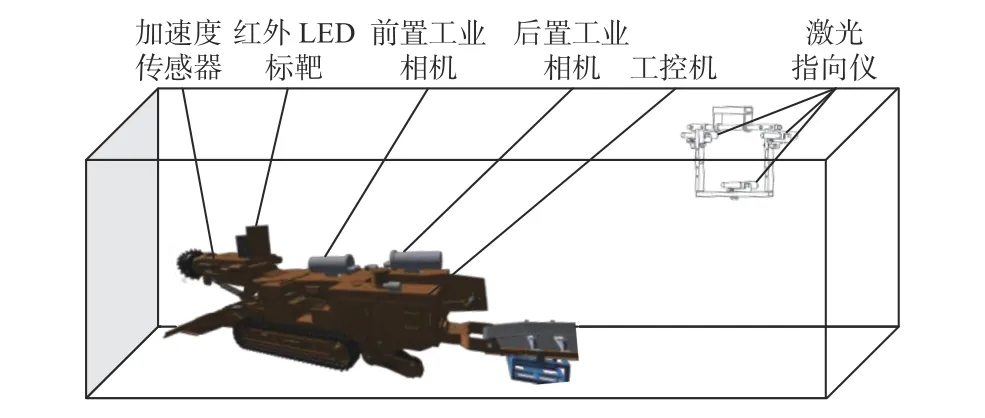
图1 悬臂式掘进机自主调速截割控制系统组成Fig.1 Composition of boom-type roadheader autonomous speed regulation cutting control system
悬臂式掘进机自主调速截割控制系统总体方案如图2 所示。该系统主要包括破岩仿真模块、截割头定位模块、截割头轨迹规划模块、截割头运动控制模块和掘进机液压系统模块。通过截割头定位模块获取掘进机截割头位姿信息,根据破岩仿真模块得到的加速度分层结果,结合截割头轨迹规划模块计算得到的截割头到达离散截割轨迹规划点所需控制量,截割头运动控制模块生成运动指令并下发至掘进机液压系统进行动作执行,最终实现掘进机自主调速截割。
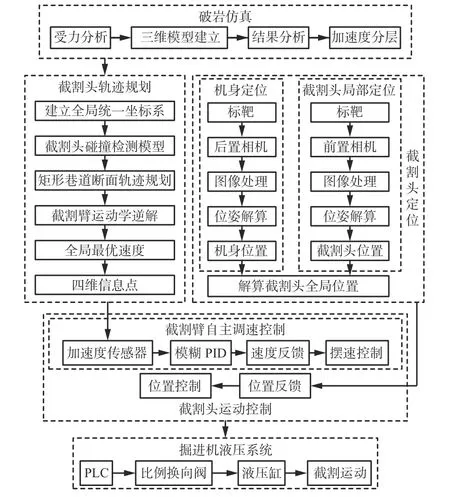
图2 悬臂式掘进机自主调速截割控制系统总体方案Fig.2 Overall scheme of boom-type roadheader autonomous speed regulation cutting control system
(1)破岩仿真模块。利用SolidWorks 软件建立截割头和煤壁的三维模型,将其导入ABAQUS 软件后进行煤岩有限元分析,获得不同截割臂摆动速度下截割头受到的反作用力,利用k-means 聚类方法进行分析后得到加速度分层结果。
(2)截割头定位模块。首先,后置工业相机采集3 个激光指向仪发出的3 条平行激光线,基于颜色分量的峰值聚类约束对激光束标靶图像进行分割,利用Hessian 矩阵求解中心线像素的法线方向,最终基于泰勒展开进行特征提取和定位,构建基于三点三线特征的掘进机机身位姿测量模型[15],获得掘进机机身位姿信息。然后,通过前置相机采集红外LED 标靶图像,利用高斯曲面拟合算法对特征点进行中心定位,使用P4P 方法对特征点的空间坐标进行求解,利用对偶四元数最优位姿计算模型完成截割头位姿检测。最后,在已知掘进机机身位姿的基础上将截割头局部位姿转换为全局位姿,得到巷道坐标系下的截割头位姿。
(3)截割头轨迹规划模块。利用截割头碰撞检测模型提前规划合适的截割轨迹,多次离散化形成离散截割轨迹规划点。利用全局最优速度模型获取截割头到达离散截割轨迹规划点的速度,通过运动学逆解计算截割头到达离散截割轨迹规划点所需的截割臂回转弧度、抬升弧度和伸长量。
(4)截割头运动控制模块。包括截割头位置控制和截割臂自主调速控制:截割头位置控制利用视觉测量结果和目标之间的差值驱动截割头运动;截割臂自主调速控制根据加速度分层结果寻找对应的目标速度,使用模糊PID 控制对截割臂摆动速度进行调节。
2 破岩仿真
掘进机截割煤壁过程中,由于截割头和煤壁之间发生不稳定的相互作用,会发生再生颤振,可通过改变截割臂摆动速度降低截割过程中产生的振动。通过模拟仿真获取截割臂不同摆动速度下截割头受到的反作用力,对截割头加速度划分等级,从而为自主调速截割控制提供数据反馈。
(1)基本假设。本文主要研究截割煤壁过程中截割头受到的反作用力与截割臂摆动速度之间的关系,为了更好地分析截割头掘进过程,作如下假设:①将截割头视为整个刚体,不考虑变形和磨损。② 将煤层视为连续、均匀的介质。③破碎后的煤块可以快速离开截割头。
(2)材料准则及失效判据。在非线性仿真软件中,Drucker-Prager 模型更适用于砂土、煤体等粒状材料,黏土类型的材料一般用修正剑桥模型。
煤层失效的塑性应变判据为
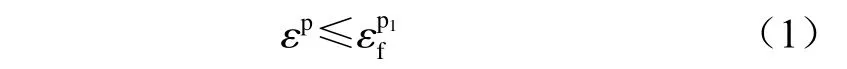
式中:εp为岩石的等效塑性应变;为岩石完全失效时的等效塑性应变。
岩石在弹性阶段的应力与应变之比可认为是线性关系,本构方程可表达为
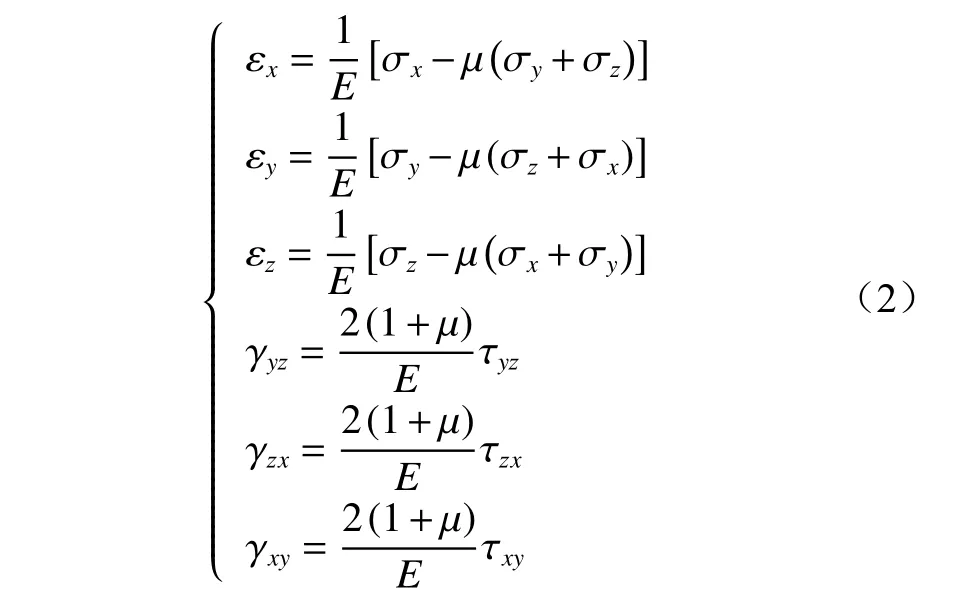
式中:εx,εy,εz为线应变分量;E为弹性模量;σx,σy,σz为 线应力分量;μ为 泊松比;γxy,γyz,γzx为角应变分量;τxy,τyz,τzx为角应力分量。
截割头受到的反作用力与截割臂摆动速度之间的关系为
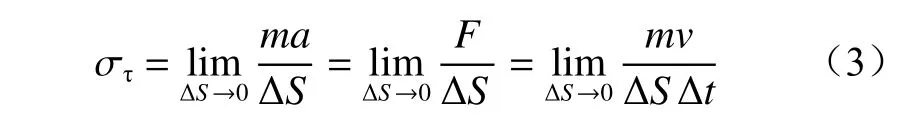
式中:στ为截割头受到的应力;m为掘进机质量;a为截割头瞬时加速度;ΔS为单位面积;F为截割头受到的反作用力;v为截割臂摆动速度;Δt为单位时间。
3 截割头轨迹规划
3.1 截割头碰撞检测模型
截割头截割煤壁碰撞检测可以简化为2 个对象两两相交测试,为降低计算量,可以采用层次包围盒算法。该算法原理是用包围盒将物体封装起来,将物体之间的碰撞检测转换为包围盒之间的相交检测,若包围盒相交,则物体间可能发生碰撞。球形包围盒结构较为简单,优点是不受旋转变化的影响,适用于运动环境中的检测。建立球形包围盒实际就是计算球心坐标和半径,球心坐标即球形表面上各点坐标的均值,半径即球心与球形表面之间的距离。球形包围盒空间状态如图3 所示,对于2 个球形包围盒(c1,c2分别为2 个球形包围盒的圆心坐标,r1,r2分别为2 个球形包围盒的半径),若|c1-c2|≤r1+r2,则可判断2 个球形包围盒相交。
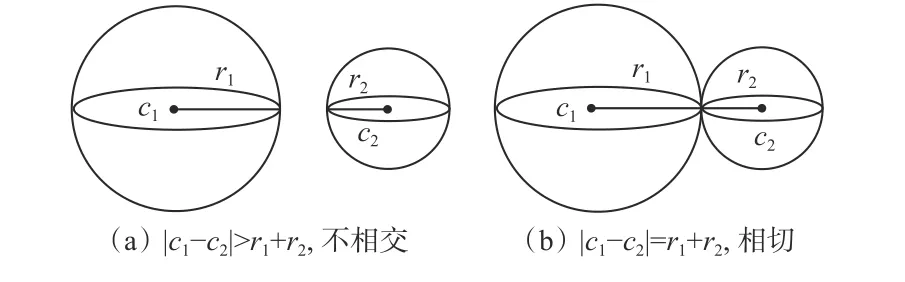
图3 球形包围盒空间状态Fig.3 Space state of spherical bounding box
采用球形包围盒对截割头进行预处理,为进一步提高包围盒的紧密性,本文使用双层包围盒的碰撞检测算法对移动中的截割头进行碰撞检测。
使用层次包围盒树[16](Bounding Volume Hierarchy Based on Tree,BVT)进行分析,在有限元分析中,三维物体一般被划分为六边形和三角形。假定有一个由若干几何对象组成的集合R,集合R被认为是多边形模型的边界即截割头的边界。设BVT(R)是集合R的边界体积层次结构,每一个节点均属于该集合。BVT(R)满足以下条件:BVT(R)内部每个节点都有2 个或多个子节点;BVT(R)内部任何一个节点下最大子节点数目的度称为树的度,记为δ;在集合R中,叶节点数目 λ和单个子集合相关联;BVT(R)的节点总数最多为 2λ-1,完整树的层次为 logδλ。离散取向多面体[17](k-Discrete Orientation Polytopes,k-DOPs)包围盒利用 ψ个平面形成的凸多面体确定边界体积,多面体的平面由半空间确定,半空间的外向法线由固定的 ψ个方向确定。截割头包围盒模型如图4 所示。
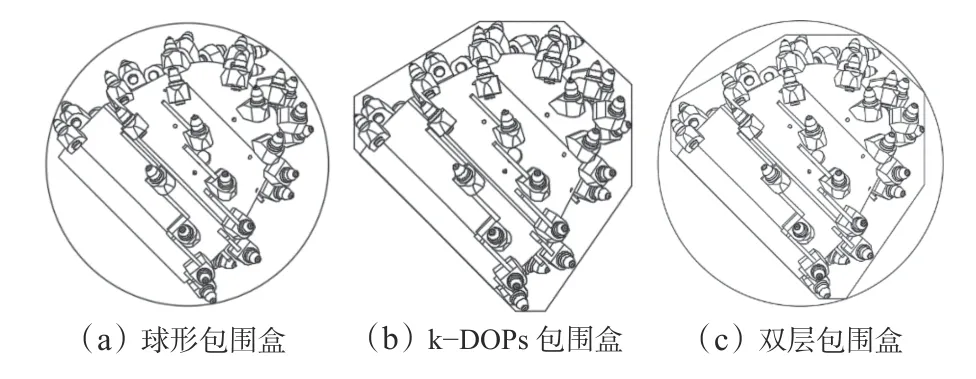
图4 截割头包围盒模型Fig.4 Cutting head bounding box model
3.2 矩形巷道断面轨迹规划
为了实现断面截割控制,针对常见的矩形巷道断面,采用改进S 形截割路线,对关键路线多次离散化,形成离散截割轨迹规划点,并以离散截割轨迹规划点为目标,控制截割头运动。首先设定巷道的宽度和高度并用实线表示,截割过程中规划的理论边界用虚线表示;然后对掘进机截割头使用双层包围盒,第1 层内部包围盒采用18-DOPs 包围盒,第2 层外层包围盒为球形包围盒;最后依照截割路线从断面底部钻进截割,按照离散截割轨迹规划点依次截割,并进行刷帮以降低两侧边界粗糙度,完成一次断面截割。矩形巷道断面轨迹规划如图5 所示。
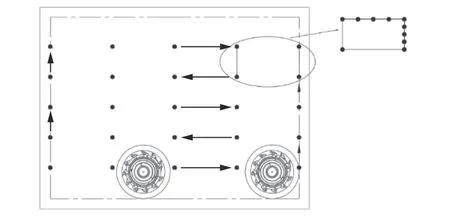
图5 矩形巷道断面轨迹规划Fig.5 Rectangular roadway section trajectory planning
将截割的煤壁定为集合A,截割头运动过程中经过的坐标点定义为集合B。集合A中的任意一个煤块都采用球形包围盒模型进行包络,集合B中截割头由于采用双层包围盒,位于外层的球形包围盒首先和集合A产生交集,由截割头碰撞检测模型进行判断,对截割臂摆动速度进行调整,之后内层18-DOPs 包围盒和集合A产生交集,判断是否到达离散截割轨迹规划点。整个截割流程如下:
步骤1:初始化。生成初始位置,设置初始速度。
步骤2:更新解集。输入目标巷道宽和高、掘进机参数和煤层信息。计算最优值,生成离散截割轨迹规划点的四维数据。
步骤3:选取局部最优。在截割过程中,若振动幅值超过阈值,则进行速度判定,进而局部调整速度。
步骤4:更新速度和位置。基于离散截割轨迹规划点更新下一时刻的位置和速度。
步骤5:判断是否达到终止条件。
3.3 截割臂运动学逆解
截割头定位的具体求解需要建立坐标系,如图6所示。OmXmYmZm为断面坐标系,以断面底线的中点为坐标系原点Om,Xm轴沿断面底部指向巷道右侧,Zm轴沿断面中线竖直向上。OcXcYcZc为相机坐标系,以相机光心为坐标系原点Oc,光轴为Zc轴。ObXbYbZb为标靶坐标系,以标靶中心为坐标系原点Ob,Yb轴方向向下过标靶右下角特征点,Zb轴方向与悬臂轴线方向重合。掘进机机身坐标系O0X0Y0Z0与回转台坐标系O1X1Y1Z1重合,以回转台中心为坐标系原点O0(O1),X0(X1)轴指向掘进机前进方向,Y0(Y1)轴指向掘进机左侧。O2X2Y2Z2为截割臂升降关节坐标系,Z2轴沿升降轴指向右侧,X2轴竖直向上。O3X3Y3Z3为截割臂伸缩关节坐标系,Z3轴与Y2轴重合。O4X4Y4Z4为截割头坐标系,以截割头末端中心为坐标系原点O4,Z4轴与Z3轴重合。O5X5Y5Z5为巷道坐标系,以巷道起点为坐标系原点O5,面向掘进方向垂直中线向右为X5轴,以底板垂直向上为Z5轴。
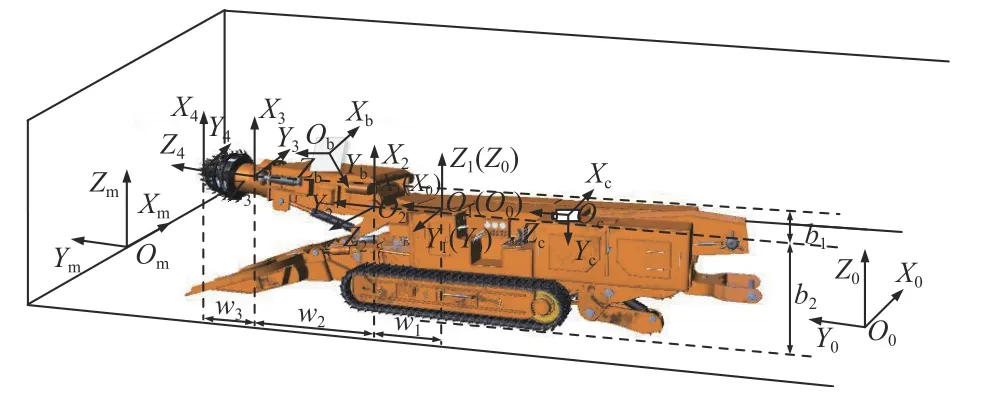
图6 坐标系建立Fig.6 Establishment of coordinate system
通过对离散截割轨迹规划点求逆解,可得截割头到达离散截割轨迹规划点所需的回转弧度、抬升弧度和伸长量。按照机器人运动学分析方法对截割臂进行运动学求解计算,可得截割头中心在掘进机机身坐标系中的位置模型:
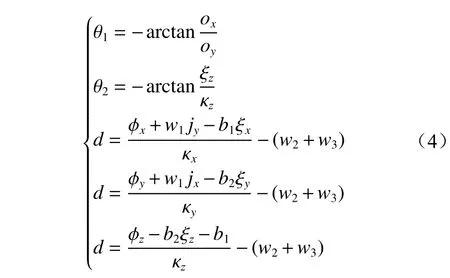
式中:θ1为 截割臂回转角度;ox,oy为截割头水平移动距离在断面坐标系的分量;θ2为截割臂抬升角度;ξx,ξy,ξz为截割头竖直移动距离在断面坐标系的分量;κx,κy,κz为截割头伸缩距离在断面坐标系的分量;d为截割头伸长量;φx,φy,φz为截割头中心点在断面坐标系的分量;w1为机身回转台中心到截割臂靠近机身关节处的距离;w2为截割臂靠近机身关节处到截割臂伸缩油缸靠近机身端的距离;w3为截割臂伸缩油缸靠近机身端到截割头前端的距离;b1为截割头中心到机身回转台中心的距离;b2为回转台中心到地面之间的距离。
3.4 全局最优速度模型
为了有效控制悬臂式掘进机截割臂的摆动速度,需要建立全局最优速度模型。对该模型作如下假定:①掘进机截割的煤壁均为软岩。② 目标断面形状为矩形。
全局最优速度模型分为决策单元、目标和约束条件。
3.4.1 决策单元
对目标巷道断面进行网格划分,截割头到达离散截割轨迹规划点的理论速度构成集合,将该集合作为决策单元Gα(α=1,2,···,N,N为离散截割轨迹规划点的数量)。
3.4.2 目标
(1)效率。掘进机截割整个巷道断面的耗时为掘进机截割头水平方向运动耗时与截割头垂直方向运动耗时之和。定义每个离散截割轨迹规划点之间的距离为u,则截割整个巷道断面所需时间为
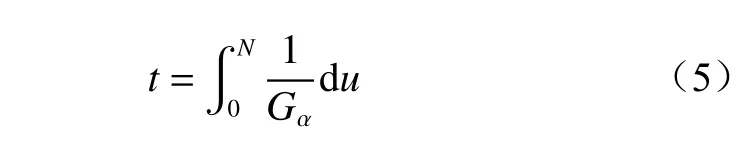
效率目标函数为
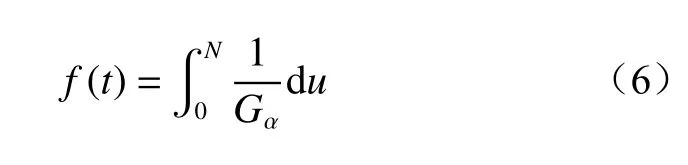
(2)反作用力。作用于质点的力可以分为彻体力和面力2 类。设在介质内部有某一点,并在其周围有体元 Δη,作用于该体元的总彻体力为P。该点的单位体积彻体力为
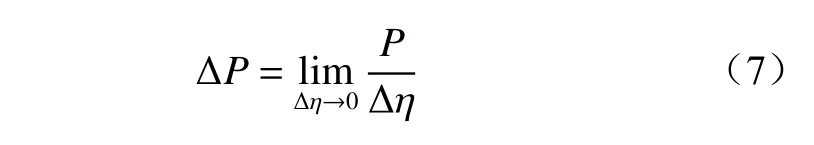
截割头受到的反作用力为
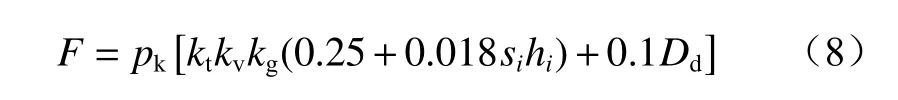
式中:pk为 被截割煤岩的接触强度;kt为镐形截齿齿形影响系数,对于旋转截割,取1.5;kv为镐形截齿几何形状影响系数,取0.95;kg为截齿的截角影响系数,取0.65;si为 第i个截齿的截线间距;hi为第i个截齿处于任意位置时的切削厚度;Dd为截齿的后刃面在牵引力方向的投影面积。
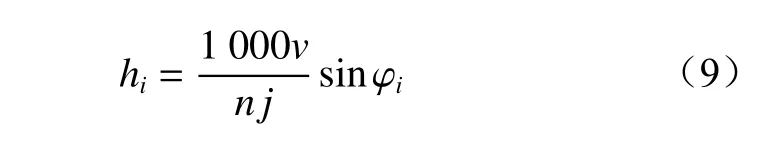
式中:n为截割头转速;j为同一截线上的截齿数;φi为第i个截齿的位置角。
反作用力目标函数为
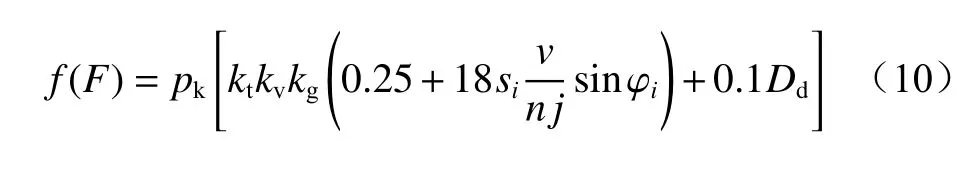
当截割臂摆动速度最大时,效率目标函数值最优;当截割臂摆动速度最小时,反作用力目标函数值最优。
3.4.3 约束条件
对截割臂摆动速度进行优化时,需要对目标函数添加约束条件:截割头有效直径应不大于截割头带截齿时的最大直径;截割臂摆动速度应小于由于较大振动导致截割头位姿测量结果产生较大误差对应的摆动速度;掘进机每次循环进刀距离小于掘进机截割臂最大伸长量;煤岩坚固性系数不大于4;巷道宽度应小于视觉测量截割头摆动距离最大值。
4 截割臂自主调速控制
PID 控制算法具有稳定性好、结构简单等特点,在工业控制领域得到广泛应用。PID 控制算法根据误差的比例、积分和微分计算出系统所需控制量,得到最优的控制参数:
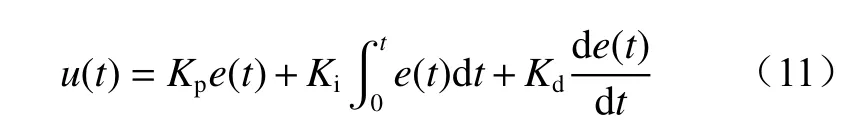
式中:Kp,Ki,Kd分 别为比例、积分、微分系数;e(t)为误差信息,t为时间。
面对掘进机截割煤壁的复杂运行环境,PID 控制算法抗干扰能力较差[18],需要调节参数,因此采用模糊PID 控制算法。以截割臂当前摆动速度与预设速度的偏差e和本次速度偏差与上次速度偏差的变化量 Δe作为输入量,以比例、积分和微分系数的增量ΔKp,ΔKi,ΔKd作为输出量,通过动态改变PID 控制参数,实现不同工况下截割臂摆动速度调节。模糊PID 控制原理如图7 所示。
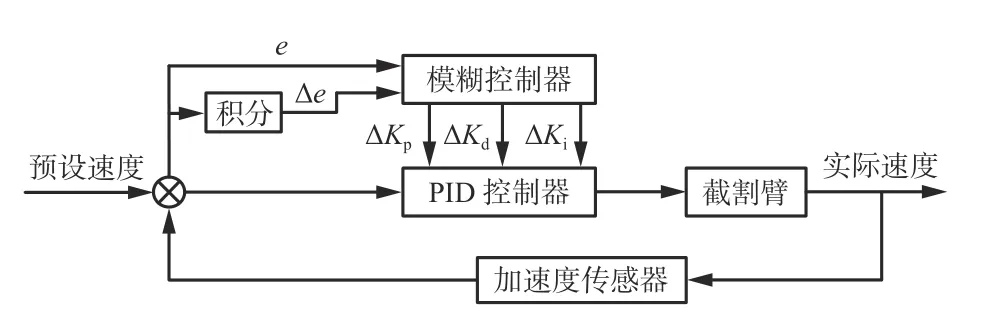
图7 模糊PID 控制原理Fig.7 Fuzzy PID control principle
通过不同速度要求下输入量的量化因子,将精确值转换为模糊值。
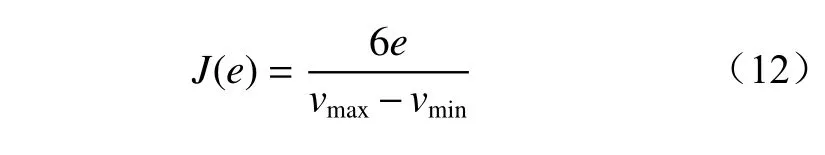
式中:J(e)为速度偏差模糊值;vmax为最大设定速度;vmin为最小设定速度。
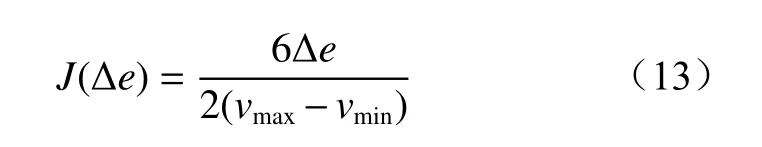
式中J(Δe)为速度偏差变化量模糊值。
根据建立的模糊控制规则(表1)和输入量的模糊结果,推理出输出量对应的模糊语言子集。
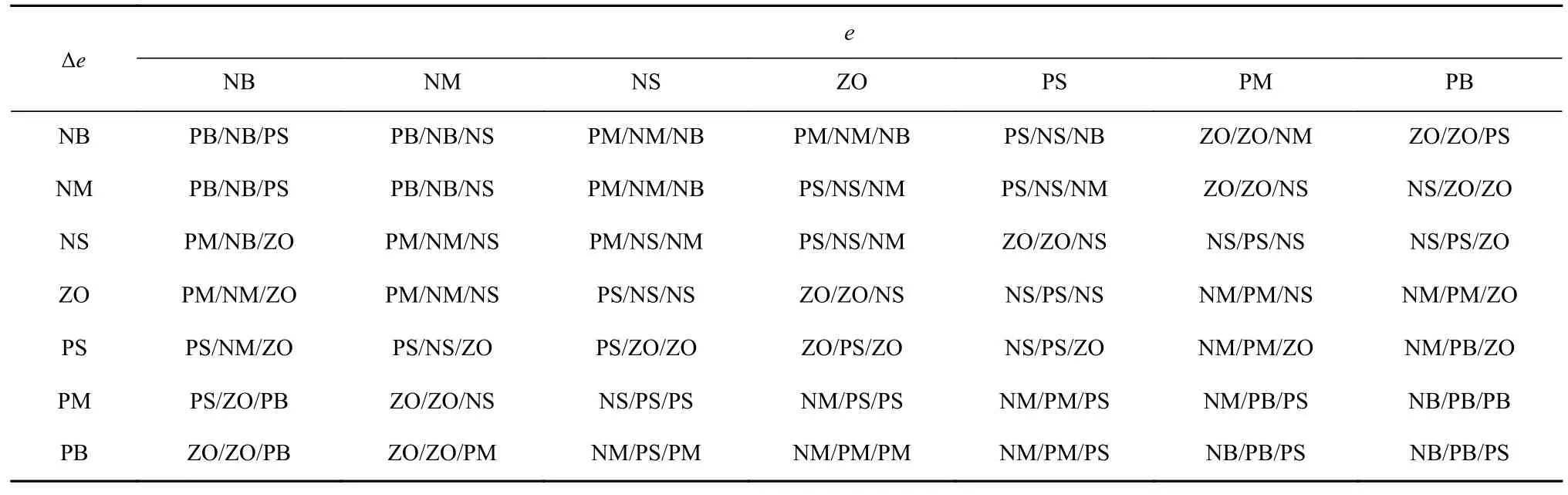
表1 模糊控制规则Table 1 Fuzzy control rules
将输出量的量化值转换为模糊PID 控制算法的实际参数,根据速度偏差调节截割臂摆动速度,实现截割臂摆动速度的动态调整。
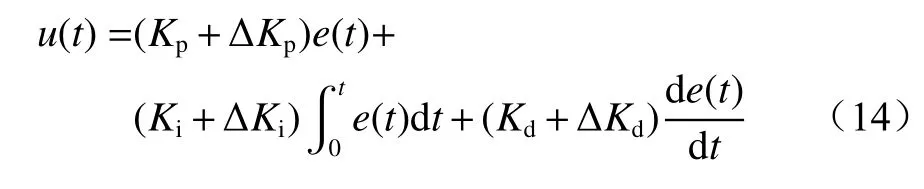
5 仿真及实验验证
5.1 加速度分层
在SolidWorks 软件中建立尺寸(长×宽×高)为4 000 mm×2 000 mm×3 000 mm 的煤层和截割头三维模型,将其转为SAT 格式文件后导入ABAQUS 中,并进行网格划分,如图8 所示。
图8 煤层和截割头的三维模型网格Fig.8 Three-dimensional model grid of coal seam and cutting head
截割头材料为钢,密度为 7.8×10-9kg/m3,弹性模量为2.1×105Pa,泊松比为0.3。煤层具体参数见表2。

表2 煤层参数Table 2 Coal seam parameters
将截割臂摆动速度分别设置为0.10,0.15,0.20,0.25,0.30 m/s,仿真不同截割臂摆动速度下截割头受到的反作用力,结果如图9 所示。可看出掘进机截割头在截割煤壁过程中会受到变化的反作用力,导致截割头产生较大振动。
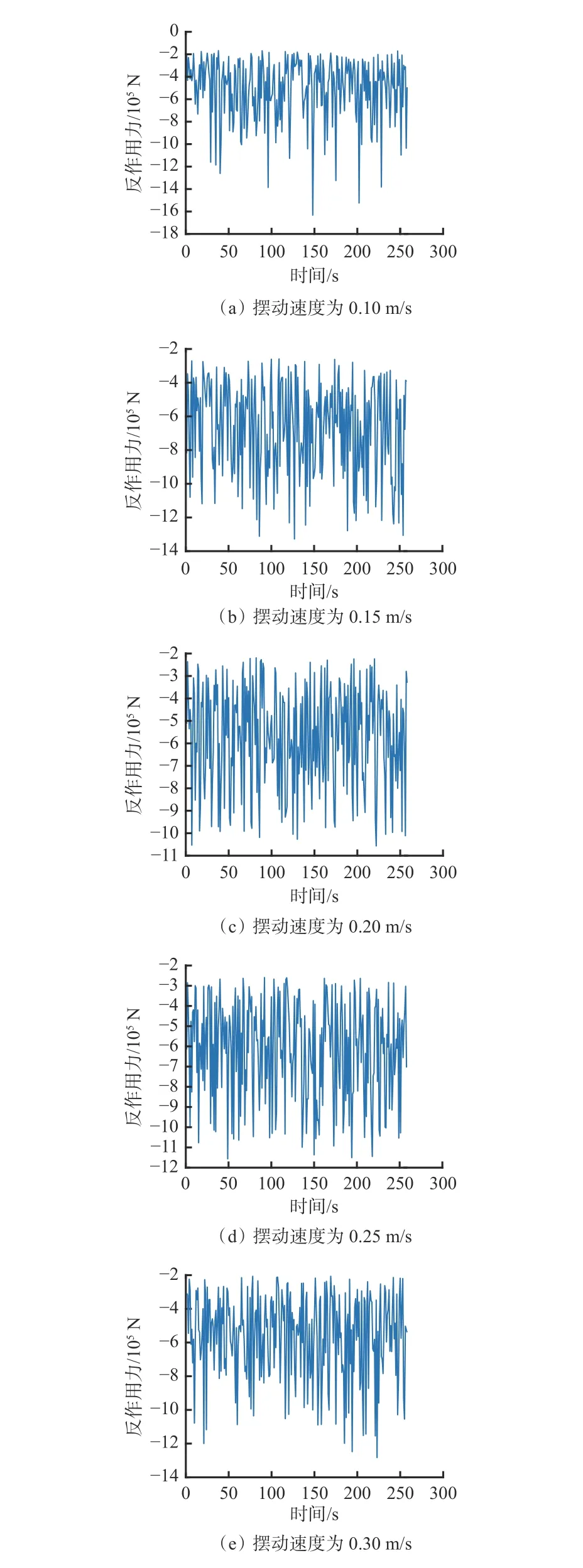
图9 不同截割臂摆动速度下截割头受到的反作用力Fig.9 Reaction force of cutting head under different swing speed of cutting arm
对不同截割臂摆动速度下截割头受到的平均反作用力数据进行滤波处理后,利用k-means 算法对数据进行聚类分析,相同摆动速度下抽取5 组数据,将数据按照摆动速度从大到小的顺序依次编号,编号和速度对应关系见表3。
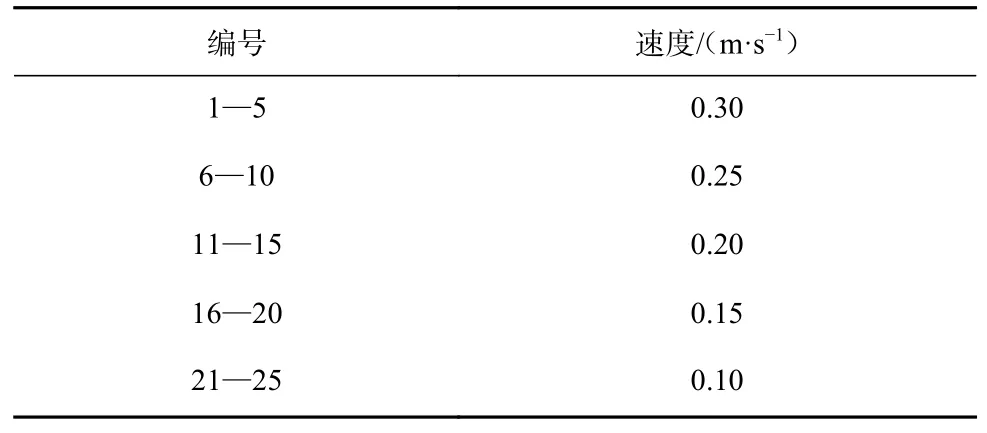
表3 编号和速度对应关系Table 3 Mapping between number and speed
设置k-means 聚类的簇数为5,计算得到5 个聚类中心,如图10 所示。当加速度为0~1.3 m/s2时,截割臂摆动速度为0.30 m/s;当加速度为1.3~2.0 m/s2时,截割臂摆动速度为0.25 m/s;当加速度为2.0~2.8 m/s2时,截割臂摆动速度为0.20 m/s;当加速度为2.8~3.5 m/s2时,截割臂摆动速度为0.15 m/s;当加速度为3.5~4.5 m/s2时,截割臂摆动速度为0.10 m/s。
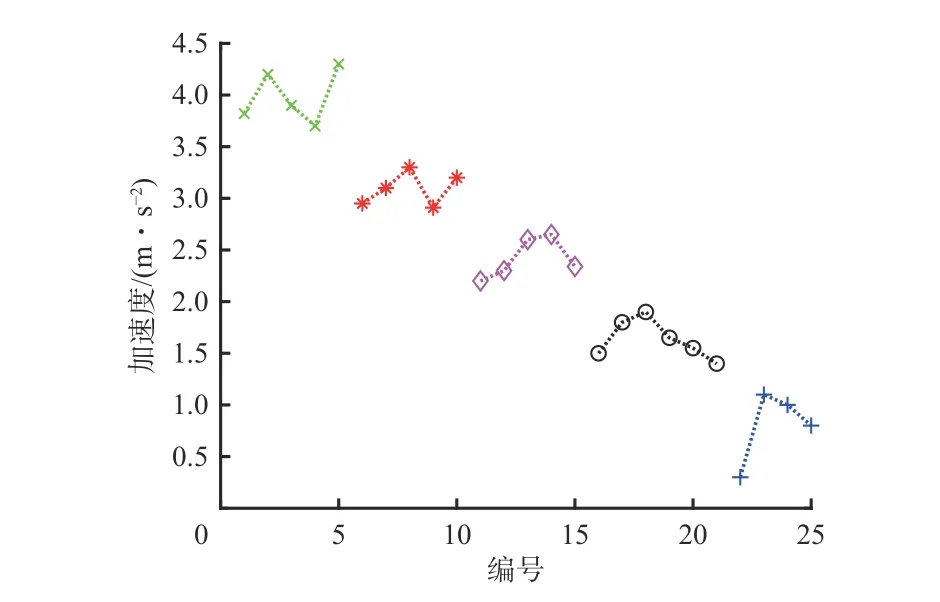
图10 聚类结果Fig.10 Clustering results
5.2 模糊PID 控制
为验证截割臂在产生较大振动时能够及时调整摆动速度,对模糊PID 控制方法进行仿真,观察截割臂摆动速度变化情况。通过Matlab 中Simulink 模块构建掘进机截割臂仿真模型,分别采用PID 控制和模糊PID 控制对模型进行仿真(幅值从0 到1 变化模拟速度信号的变化),结果如图11 所示。可看出采用模糊PID 控制可使模型在波动较小、无超调、调节时间较短情况下达到稳定状态,在控制精度较高、响应速度较快的情况下保证掘进机截割臂摆动速度达到目标值。
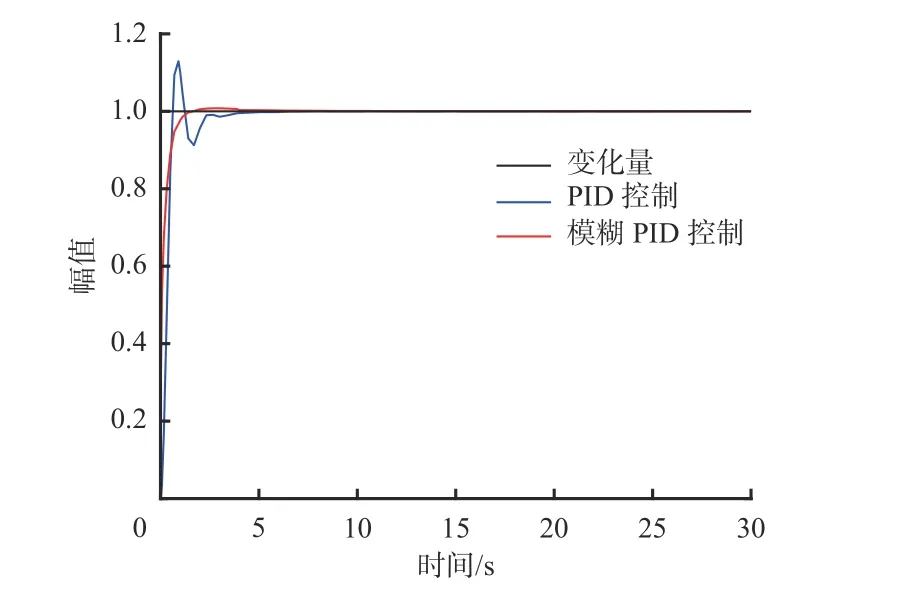
图11 PID 控制和模糊PID 控制效果对比Fig.11 Effect comparison of PID control and fuzzy PID control
5.3 掘进机自主调速截割控制
为验证掘进机自主调速截割控制的可行性,构建悬臂式掘进机虚拟调速截割控制实验平台,如图12 所示,该平台由本地控制模块、远程虚拟模块和振动模块组成。

图12 悬臂式掘进机虚拟调速截割控制实验平台Fig.12 Experimental platform of boom-type roadheader virtual speed regulation cutting control
振动模块中的加速度传感器采集的振动信号经解析后传输至本地控制模块。本地控制模块中防爆计算机上安装基于VS+QT 开发的自主调速截割控制系统,在程序的管理员界面上输入目标巷道宽度、高度和煤层地质条件等初始参数,保存后完成程序的初始化操作。本地控制模块接收到振动模块发来的信号后,经过计算输出控制指令并通过MQTT 通信协议传递给远程虚拟模块。远程虚拟模块基于Unity3D 平台开发,接收到本地控制模块发送的数据后,驱动虚拟掘进机模型截割臂按照控制指令移动,同时虚拟掘进机模型反馈截割头实时位姿数据到本地控制模块,不断循环以上步骤,最终实现掘进机自主调速截割控制。
参考实际工况,设置巷道宽度为3 000 mm,高度为3 000 mm,每次截割深度为400 mm,岩石坚固性系数为2,w1=776 mm,w2=2 441 mm,w3=2 305 mm,b1=297 mm,b2=1 613 mm。通过运动学逆解计算可获得截割头到达离散截割轨迹规划点所需的回转弧度、抬升弧度和伸长量等信息,结合获取的速度信息,得到离散截割轨迹规划点的四维数据,见表4。
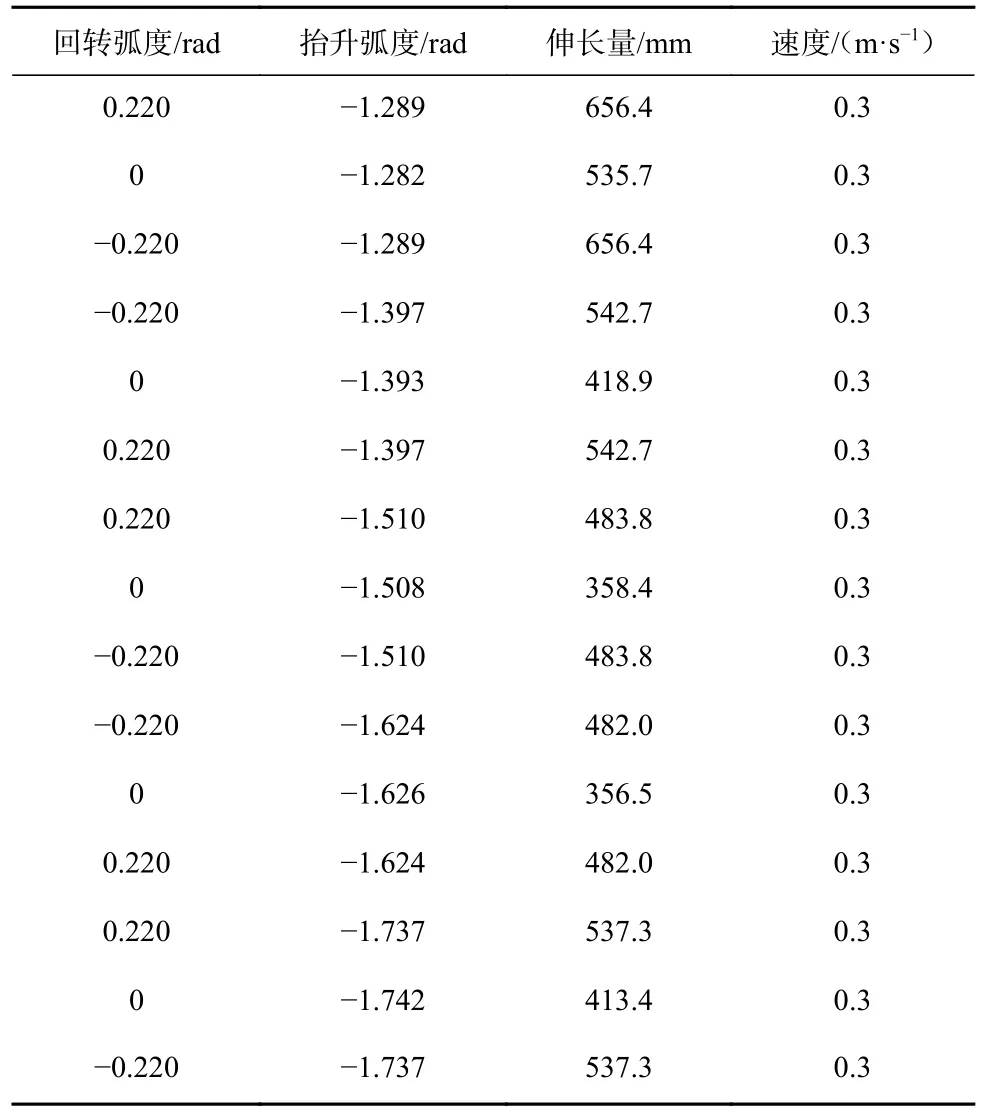
表4 离散截割轨迹规划点的四维数据Table 4 Four-dimensional data of discrete cutting trajectory planning points
振动模块采集到的截割头加速度和本地控制模块输出的截割臂摆动速度如图13 所示。可看出截割头开始截割时,加速度发生突变,截割臂摆动速度可以及时准确地随着截割头加速度的变化调整到目标摆动速度。
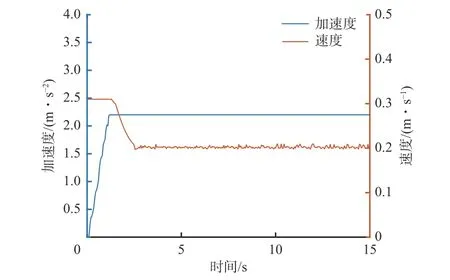
图13 模拟截割结果Fig.13 Simulated cutting results
设置3 种不同截面面积的巷道:1 号巷道宽度为4 000 mm,高度为3 000 mm;2 号巷道宽度为4 000 mm,高度为2 500 mm;3 号巷道宽度为3 000 mm,高度为2 500 mm。采用定速截割控制和自主调速截割控制分别对3 种巷道进行截割,实验结果见表5(为模拟真实情况下从控制指令下发到截割头运动之间的通信延迟,将远程虚拟模块获取当前截割头信息的脚本刷新频率设置为400 ms)。可看出相对于定速截割控制,使用自主调速截割控制完成的巷道断面宽度规格偏差降低了37%,高度规格偏差降低了17%。根据煤炭行业标准MT/T 5009-1994《煤矿井巷工程质量检验评定标准》的规定,掘进过程中巷道宽度规格偏差是无中线测全宽距离在-50~+250 mm 为合格,0~+200 mm 为优良,巷道高度规格偏差是无腰线测全高距离在-50~+250 mm 为合格,0~+250 mm为优良,实验数据基本符合要求。
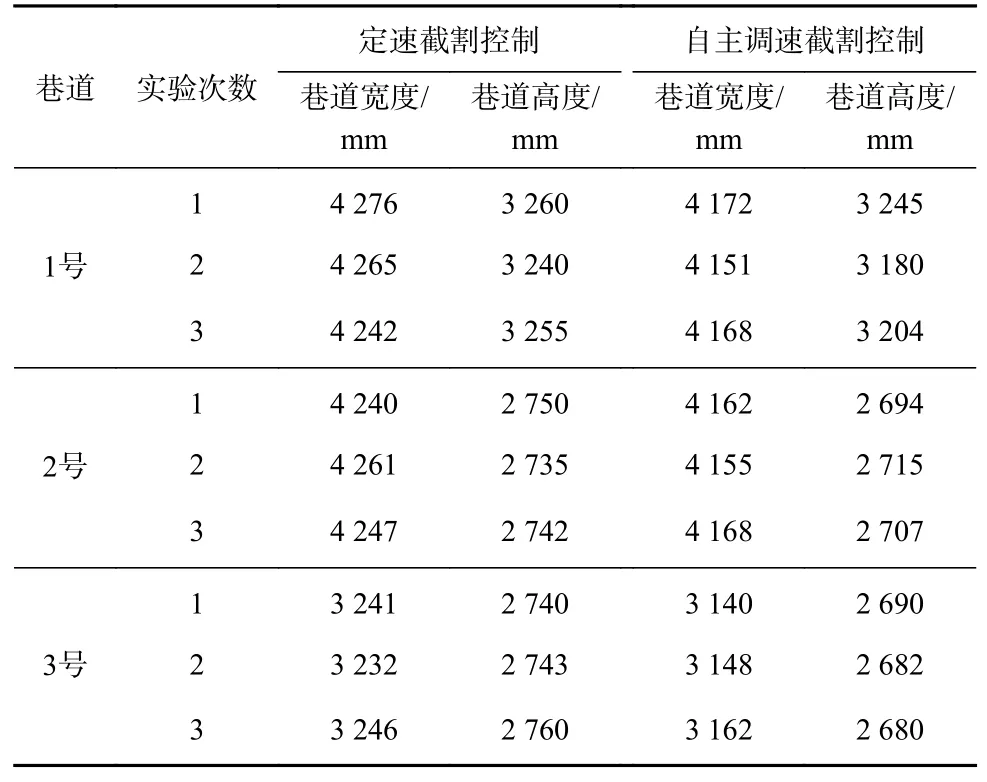
表5 巷道断面截割实验结果Table 5 Experimental results of roadway section cutting
6 结论
(1)利用非线性仿真软件分析了掘进机截割煤壁过程中截割头受到的反作用力和截割臂摆动速度之间的关系,得到截割臂摆动速度和截割头加速度之间的关系,对截割头加速度进行分层,以便根据加速度分层结果寻找对应的目标速度。
(2)以截割头碰撞检测模型为基础,构造采用改进S 形截割路线设计的离散截割轨迹规划点,利用全局最优速度模型求解截割头运动至离散截割轨迹规划点的速度,利用运动学逆解计算获得截割头到达离散截割轨迹规划点所需的控制量,并通过模糊PID 控制驱动截割头完成断面截割。
(3)搭建掘进机虚拟调速截割控制实验平台进行巷道断面截割实验,结果表明,采用自主调速截割控制的断面成形质量较高,宽度规格偏差降低了37%,高度规格偏差降低了17%,满足MT/T 5009-1994 巷道成形质量要求。
