基于图像计数酿酒酵母的统计分析
2023-02-21李雪松陈翔宇李蒙蒙徐娟林丽军陆利霞崔晓文熊晓辉
李雪松,陈翔宇,李蒙蒙,徐娟,林丽军,陆利霞,崔晓文,熊晓辉
(南京工业大学 食品与轻工学院,南京,211800)
传统的平板计数法是国际公认的权威微生物计数。但是平板计数培养时间长,有时具有滞后性[1],其次平板计数法仅计数可培养的活菌,对于不可培养的微生物无法进行检测[2]。目前已有许多新型的微生物计数方法,如还原显色法、阻抗法、ATP生物发光法、荧光仪法、电化学发光法等[3-7]。这些方法间接、快速获知菌体数量,但极易受环境及基质影响。对菌体逐个计数的直接计数方法更快速、准确,如流式细胞仪可对高速流动的微生物个体逐个检测,且可对死、活菌分别计数[8]。目前流式细胞仪已经应用于微生物的检测[9-11],但流式细胞仪价格昂贵,检测成本高。
基于微生物图像计数的方法是另一种成本更低的直接计数方法,其原理是显微镜镜检技术,计数载体通常为具有固定微体积的计数板或具有固定面积的滤膜。而根据载体的不同,图像计数定量微生物浓度的统计方法也有所不同。血球计数板使用最多,其计数室深度为0.1 mm,容积为0.1 μL,可计数真菌及一些形态较大的细菌[12]。而滤膜法是将试样中的微生物细胞过滤在滤膜上,在显微镜下计数一定面积滤膜上的细胞数量,进而推算出样品中微生物的浓度[13-14]。因此在图像计数中,定量结果都是基于部分体积或面积中细胞数量推算的结果。结果的准确推算基于2个假设:微生物细胞的分布是均匀的;对部分体积或面积中微生物统计的参数可以代表总体[15]。然而现有的研究中很少对以上的假设进行分析和说明,且目前图像计数没有统一的分析方法。其次,关于图像计数和平板计数的结果间的比较未见报道。
本研究使用具有固定体积的微型计数板,将不同浓度的酿酒酵母样品经美兰染色后加入微型计数室中,智能手机获取菌体的显微图像,并对图像中的活菌进行计数。本研究对图像计数过程进行了广泛的统计学分析,并与GB 4789.15—2016中的平板计数法进行了对比,以期为微生物图像计数的应用提供参考。
1 材料与方法
1.1 材料与试剂
酿酒酵母(Saccharomycescerevisiae)ATCC 9080,本实验室保存;0.01 mol/L PBS(pH 7.45),0.1%碱性美兰染色液,上海生物工程有限公司;酵母浸出粉葡萄糖(yeast extract peptone dextrose,YPD)培养基、马铃薯葡萄糖琼脂(potato dextrose agar,PDA)培养基,青岛海博生物技术有限公司。所有的试剂与培养基均用超纯水配制。
1.2 仪器与设备
自制微型计数板,聚甲基丙烯酸甲酯制作,计数室规格24 mm×4.15 mm×0.1 mm;BM1000生物显微镜,南京江南永新光学有限公司;Redmi k40智能手机,北京小米科技有限责任公司;SHP-100智能生化培养箱,上海三发科学仪器有限公司。
1.3 实验方法
1.3.1 酿酒酵母菌液的制备
将保存的酿酒酵母接种于YPD培养基中,37 ℃恒温振荡培养12 h,连续活化2~3次。取37 ℃下培养18 h的菌液1 mL于1.5 mL离心管中1 500 r/min离心5 min,去上清液,菌泥用同体积的无菌PBS重悬,以10倍稀释制得不同浓度的样品液,备用。
1.3.2 酿酒酵母显微图像的获得及菌体计数
1.3.2.1 酿酒酵母美兰染色
取100 μL酿酒酵母悬液,涡旋分散,加入100 μL美兰染色液,室温染色3 min,吸取染色后的菌液,加入并充满微型计数室。未染色的为活酵母细胞,蓝色的为死亡酵母细胞。
1.3.2.2 酿酒酵母计数用显微图像获得
所使用显微镜物镜40倍,目镜10倍,图像总放大倍数为400倍,单个显微镜视野的直径为0.45 mm。通过智能手机获得显微镜图像,每个图像对应一个完整的视野,用于酿酒酵母图像计数。通过智能手机从每个微型计数室获得均匀分布、不重叠、用于定量计数的200个图像。
1.3.2.3 图像中酿酒酵母的计数
使用Image J[16]软件对获得的图像进行酵母菌计数,分别计数每张图像中的活菌数量和死菌数量,每个图像中活菌数量计为yi。
1.3.3 酿酒酵母浓度平板计数
依据GB 4789.15—2016《食品安全国家标准 食品微生物学检验霉菌和酵母计数》对酿酒酵母浓度进行平板计数。
1.3.4 图像计数统计分析
使用1.3.1制备的不同浓度酿酒酵母样品,对每个样品进行13、25、50、100、200个图像的采集,并计数每个图像中酿酒酵母数量。对计数结果进行统计学分析[17],每个样品重复3次。
1.3.4.1 箱线图的制作
制作不同图像中酿酒酵母数量的箱线图,图中大于Q3+1.5IQR和小于Q1-1.5IQR的数量值判断为异常值,其中Q1为下四分数,Q3为上分位数,四分位间距IQR=Q3-Q1。图像中酿酒酵母数量平均值的计算如公式(1)所示:
(1)
式中:n, 计数的图像数量;yi, 每个图像中活菌数量。
1.3.4.2 统计参数的分析
1.3.4.3 图像计数定量样品中酿酒酵母浓度的计算

(2)
式中:n,计数的图像数量;V,单个图像体积,0.016 μL;2,样品加入等体积美兰染色液的稀释系数。
1.3.5 图像计数与平板计数结果的不确定度
对于图像计数和平板计数过程,都是通过对不同视野图像或平行平板重复计数计算得到最终定量结果。因此在重复计数过程中,不同图像或平板中菌体或菌落数量的差异性会造成定量结果的不确定,根据JJF1059.1—2012《测量不确定度评定与表示》的规定计算不确定度。不确定度也反映了对应分析过程的误差水平[18]。
1.3.5.1 图像计数结果不确定度的计算
以单个图像计数定量样品中酿酒酵母浓度如公式(3)所示:

(3)
基于单个图像计数定量结果的标准不确定度(以标准偏差表示)的计算如公式(4)所示:
(4)
相对标准不确定度的计算如公式(5)所示:
(5)
最终对样品的定量结果是对n个图像计数结果的平均值。因此,最终图像计数定量结果的标准不确定度按公式(6)计算,相对标准不确定度按公式(7)计算:
(6)
(7)
根据不确定度计算了定量结果的95%置信区间,如公式(8)所示:
(8)
式中:t0.025临界值由自由度为n-1的学生氏t分布确定。
1.3.5.2 平板计数结果不确定度的计算
平板计数方法按GB 4789.15—2016所规定的操作执行,但对连续2个稀释梯度,每个稀释梯度均倾注了50个平板。对100个平板进行酿酒酵母菌落计数,每个平板中菌落数标记为XAi,XBi。
基于单个平板计数结果的标准不确定度(以标准偏差表示)的计算如公式(9)(10)所示。相对标准不确定度如公式(11)所示:
(9)
(10)
(11)
式中:A,第一稀释梯度;B,第二稀释梯度;i,每个稀释梯度中的平行平板,i=1,2,3,…50。根据国标方法的要求,选择2个稀释梯度的菌落数在10~150个之间的平板为有效平板,有效平板数量记为m。Xi,有效平板中的菌落数,对于第一稀释梯度Xi=XAi,对于第二稀释梯度Xi=0.1XBi。
在GB 4789.15—2016平板计数中连续2个稀释梯度各倾注2块平板,因此平板计数的结果由4块平板得出,故n取4。得到平板计数结果的标准不确定度的计算如公式(12)所示,相对标准不确定度计算如公式(13)所示:
(12)
(13)
1.4 数据统计与分析
使用SPSS 22.0软件和Origin 2018软件对实验数据进行统计分析并作图。
2 结果与分析
2.1 不同浓度酿酒酵母样品图像中菌体数量分布
选取了105~107CFU/mL浓度范围内的5个样品,浓度由高至低标记为A~E。各样品图像中酿酒酵母的数量如图1所示(图1-a~1-e对应样品A~E;Ⅰ~Ⅲ表示每一样品的3次重复图像计数),箱体线段至上而下依次表示最大值、上四分位数、中位数、下四分位数和最小值,箱体内散点为平均数,箱体外为异常值。由图1可知,酿酒酵母数量在不同图像中存在很大的差异。如样品A,单个图像中酿酒酵母计数结果最多为449个,最少为151个。并且样品浓度为105CFU/mL,不同图像中酿酒酵母数量差异更大,如样品E的图像中酿酒酵母数量最多为11个,单个图像中出现无菌体的现象。每个样品中部分组别的箱线图中可观察到异常值,如样品A的重复2(图1-a-Ⅱ),图像数量为200时,存在异常值449、201;样品B的重复1(图1-b-Ⅰ),图像数量为25时,存在异常值104。表明溶液中细胞分布不均匀,从而导致定量结果的不确定。
对样品A、B、C不同重复的箱线图进行分析。发现在不同计数图像数量时,平均数均属于同一水平,且与中位数基本重合;随计数图像数量的变化,数据的分布范围存在差异,但箱体宽度基本一致,表明数据具有相似的集中程度。分析样品D、E不同重复的箱线图,随着计数图像数量增加到50个时,平均数逐渐达到同一水平,并接近于中位数;此时箱线图数据的分布范围与箱体的宽度也趋于一致,表明不同数据组之间具有相似的分布特点。对5个样品,3个重复,不同计数图像数量下得到的共75组数据进行正态分布检验(Shapiro-Wilk Test,P>0.05),显示仅有40组数据通过检验。
在一些基于显微图像计数的微生物计数方法中,一定区域中微生物的分布常被建模为泊松分布[19]或正态分布[20]。本研究中基于箱线图的形状,在不同的图像中酿酒酵母的数量成对称分布,不同计数图像数量的箱线图也说明对分布方式的准确判断需要足够数量的图像。
2.2 计数图像数量对酿酒酵母计数结果的影响
2.2.1 计数图像数量对酿酒酵母计数中位数的影响
在统计学中,中位数受极端数据的影响较小,是反映一组数据特征的重要参数[17]。不同计数图像数量时酿酒酵母计数的中位数及变化趋势见图2。对于106~107CFU/mL浓度的样品A、B、C,当计数图像的数量由13个增加至200个时,中位数依次为样品A(299.50~301.67),样品B(69.50~70.67),样品C(27.33~28.00)(图2-a),且其变化均小于5%,见图2-b。而对于105CFU/mL浓度的样品D、E,随统计图像数量的增加,酿酒酵母计数的中位数逐渐趋于稳定,当数量达到50个以上时,样品D中位数趋于7,样品E中位数为2;此时中位数数值变化小于10%(图2-b)。结果表明,计数一定数量的图像后,计数中位数可以代表总体的数量特征,可作为图像计数统计分析的参数。酿酒酵母浓度为106~107CFU/mL时,需计数的图像数量为13个;酿酒酵母浓度为105CFU/mL时,需计数的图像数量为50个。

a-3.5×107 CFU/mL;b-7.3×106 CFU/mL;c-3.5×106 CFU/mL;d-7.5×105 CFU/mL,e-2.7×105 CFU/mL图1 不同统计图像数量中酿酒酵母数量箱线图Fig.1 Box diagram of the cell number of S.cerevisiae by different image amounts
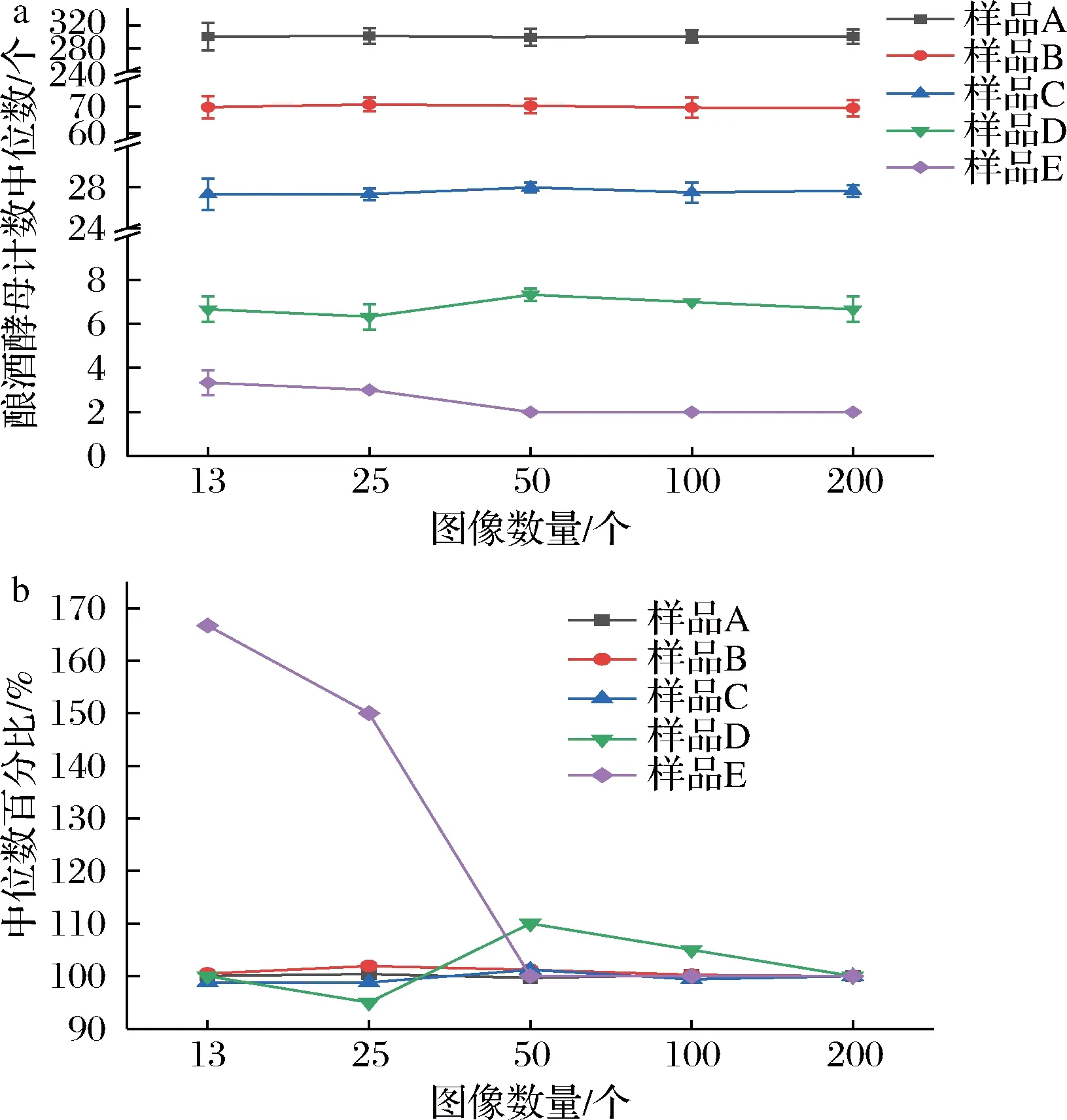
a-不同计数图像数量时中位数;b-不同图像数量中位数与200个图像计数中位数的百分比图2 酿酒酵母计数中位数随计数图像数量的变化(n=3)Fig.2 Median change of S.cerevisiae by the different image amounts(n=3)
2.2.2 计数图像数量对酿酒酵母计数平均数的影响
计数不同数量的图像后得到的图像中酿酒酵母数量的平均数及百分比变化趋势见图3。样品A、B、C图像计数的平均数均大于20个(图3-a),计数平均数随图像数量变化小于5%(图3-b),13个图像计数平均数即稳定。
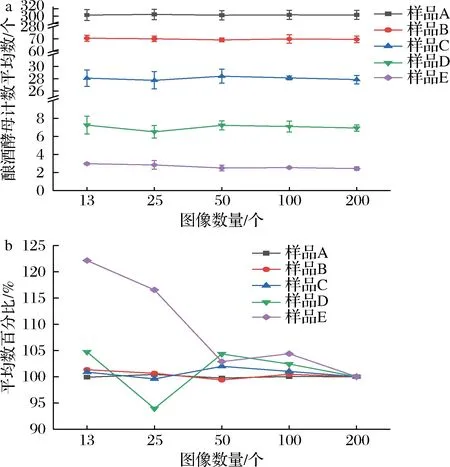
a-图像中酿酒酵母数量的平均数;b-不同图像数量计数平均数与200个图像计数平均数的百分比图3 酿酒酵母计数平均数随计数图像数量的变化(n=3)Fig.3 Average change of S.cerevisiae by the different image amounts(n=3)
对于样品D、E,图像计数的平均数小于10个,当计数图像数量为13和25时,酿酒酵母计数平均数差异大;当图像数量达到50个时,平均数随图像数量变化小于5%(图3-b)。分析表明,对一定数量的图像计数后得到的计数平均数可反映总体的数量特征,可作为图像计数统计分析的参数。在本研究中,酿酒酵母浓度为106~107CFU/mL时需统计图像数量至少为13个,浓度为105CFU/mL时需统计图像数量至少为50个,所得平均数更反映实际细胞数量。
2.2.3 不同图像间酿酒酵母数量的相对标准偏差随计数图像数量的变化
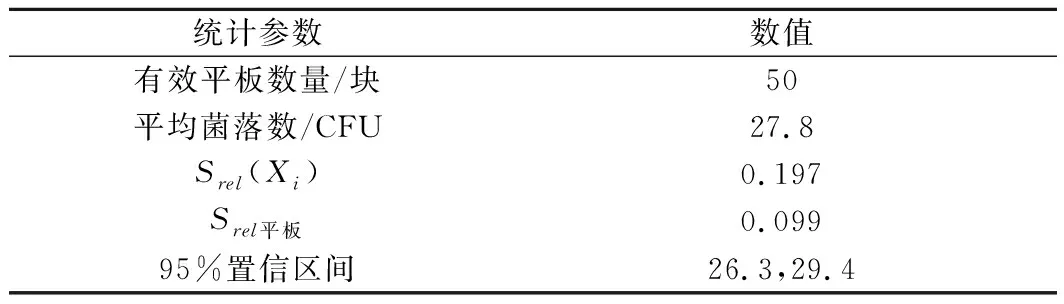
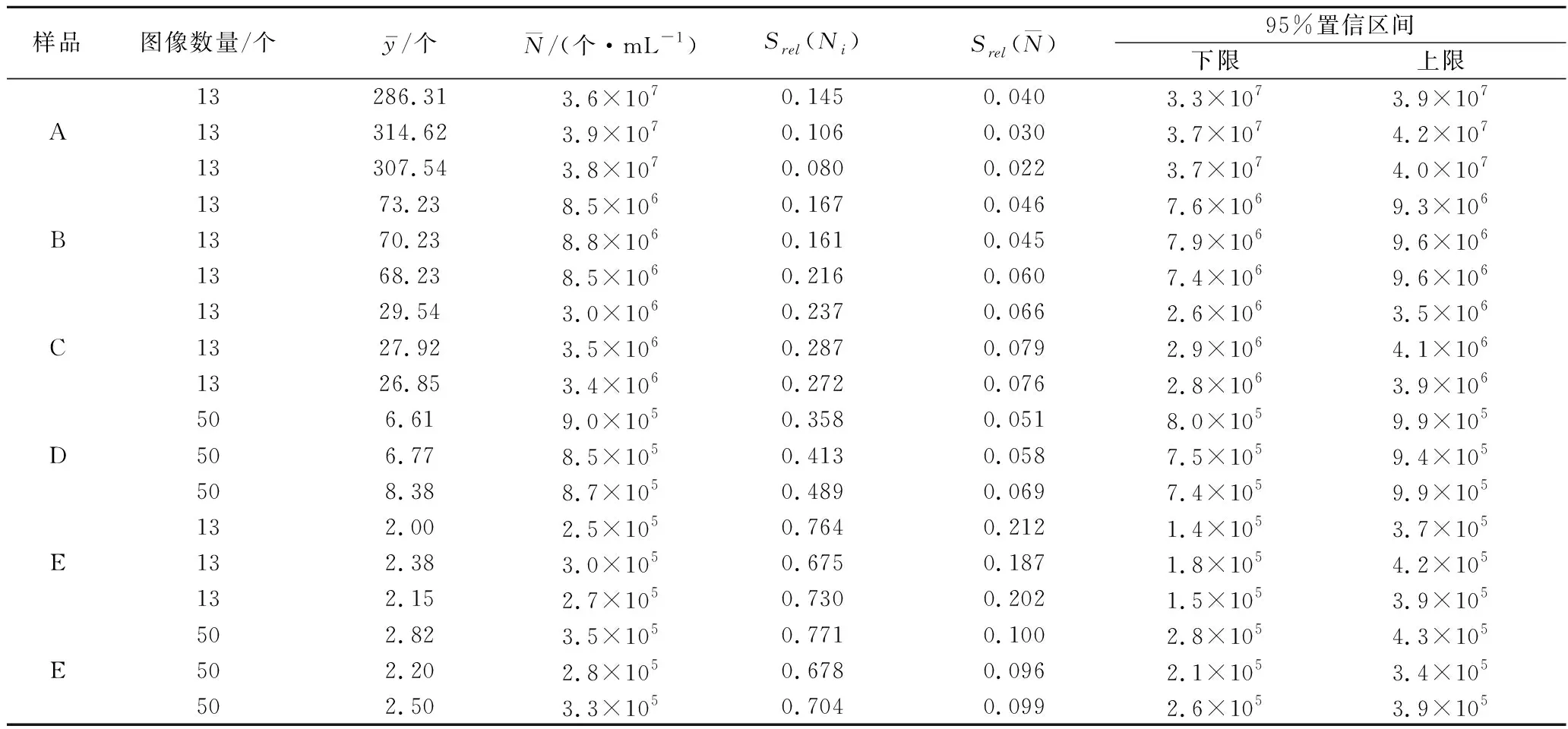
相对标准偏差(relative standard deviation,RSD)为反映不同图像中酿酒酵母数量的差异性的统计学参数,也用于计算图像计数结果的不确定度。如图4-a,不论计数图像数量为多少,均存在RSDA a-不同计数图像数量时酿酒酵母数量的RSD;b-不同图像数量下RSD与200个图像下所得RSD的百分比图4 酿酒酵母数量的RSD随计数图像数量的变化(n=3)Fig.4 RSD change of S.cerevisiae by the different image amounts(n=3) 2.3.1 图像计数与平板计数结果的不确定度 由表1可知,酿酒酵母平板计数的相对标准不确定度为0.099,95%置信区间下限为26.3,上限为29.4。 表1 平板计数统计结果Table 1 Statistical results by plate counting 表2 图像计数统计结果Table 2 Statistical results by image counting 计数的视野数量和视野中目标物的数量决定了计数误差或精密度水平[21]。如在我国水利部SL 733—2016《内陆水域浮游植物监测技术规范》中规定每个视野的浮游植物平均数须对应相应的计数视野数。美国标准《Standard Methods for the Examination of Water and Wastewater(22nd)》对水中藻类的计数中要求在滤膜的每个视野中存在10~20个自然单位。本研究也证明了增加统计的图像数量可以有效提高图像计数的精确度。而伴随着数字图像处理技术的广泛研究与应用,对超大量图像实现自动分析变得简单[22]。因此图像计数有望得到更精确的定量结果。其次,本研究中计算的不确定度仅是指2种计数过程中由于重复计数所带来的不确定度,而并非总的不确定度。但研究表明,重复的平板计数给计数结果的不确定度带来了最大的贡献[23]。而KIRCHMAN等[24]使用显微镜计数细菌的研究也表明,不同视野计数的变异是计数结果总变异的最大来源,占总变异的60%~80%。 2.3.2 两种计数结果的比较 对105~107CFU/mL酿酒酵母样品分别通过平板计数和图像计数进行定量分析,酿酒酵母样品浓度进行对数转换,结果见表3。采用双尾配对t检验对2种定量计数结果进行分析,表明图像计数结果显著大于平板计数结果(P<0.05)。并且图像计数结果的变异系数均在10%以下,小于平板计数,可重现性更好。 表3 平板计数和图像计数得到的酿酒酵母样品浓度Table 3 Cell concentration of S.cerevisiae by plate counting and image counting 对2种结果进行线性回归分析,结果如图5所示。线性回归结果表明,在105~107CFU/mL时,酿酒酵母样品采用图像计数与平板计数存在显著的相关性(P<0.001,R2=0.999 6)。2种定量结果尽管在统计学上存在显著差异,但对其差值进行比较,在试验的所有样品中,图像计数与平板计数定量样品浓度的对数值相差均小于0.1,所计数的样品中酿酒酵母浓度相差均未出现数量级上的差异。表3表明,图像计数结果的变异系数均小于平板计数结果的变异系数,也说明了图像计数变化较小。依据中国检验检疫科学研究院测试评价中心微生物定量(如食品中菌落总数)能力验证(实验室间,参与者)结果判断,能力验证评价标准按照|Z|值进行评价,|Z|<2.0为满意结果[25]。酿酒酵母浓度为105~107CFU/mL范围内,图像计数结果与平板计数结果一致,且前者精确度与重复性更好。 图5 两种定量结果的线性关系Fig.5 The linear relationship between the results of two quantitative analyses 本研究以105~107CFU/mL的酿酒酵母为分析对象,表明需一定数量的图像计数可以得到总体的数量特征,计数平均数和中位数可作为图像计数统计分析的参数。在本研究对酿酒酵母样品的图像计数中,酿酒酵母浓度为106~107CFU/mL时需统计图像数量至少为13个,浓度为105CFU/mL时需统计图像数量至少为50个,图像计数方法不确定度较小,并且通过增加计数图像的数量可以进一步减小结果的不确定度,使结果更加精确。对酿酒酵母样品图像计数和平板计数比较表明,在105~107CFU/mL时,酿酒酵母样品采用图像计数与平板计数存在显著的相关性,2种计数结果的对数值相差均小于0.1,图像计数结果的变异系数均小于平板计数结果的变异系数。 目前随着微流控技术与数字图像处理技术的快速发展,图像计数呈现出动态化、自动化的特点,使得基于图像计数的微生物计数方法具有了更大的发展空间[26-27]。本研究的成果为新型图像计数方法的开发与使用提供了统计分析依据。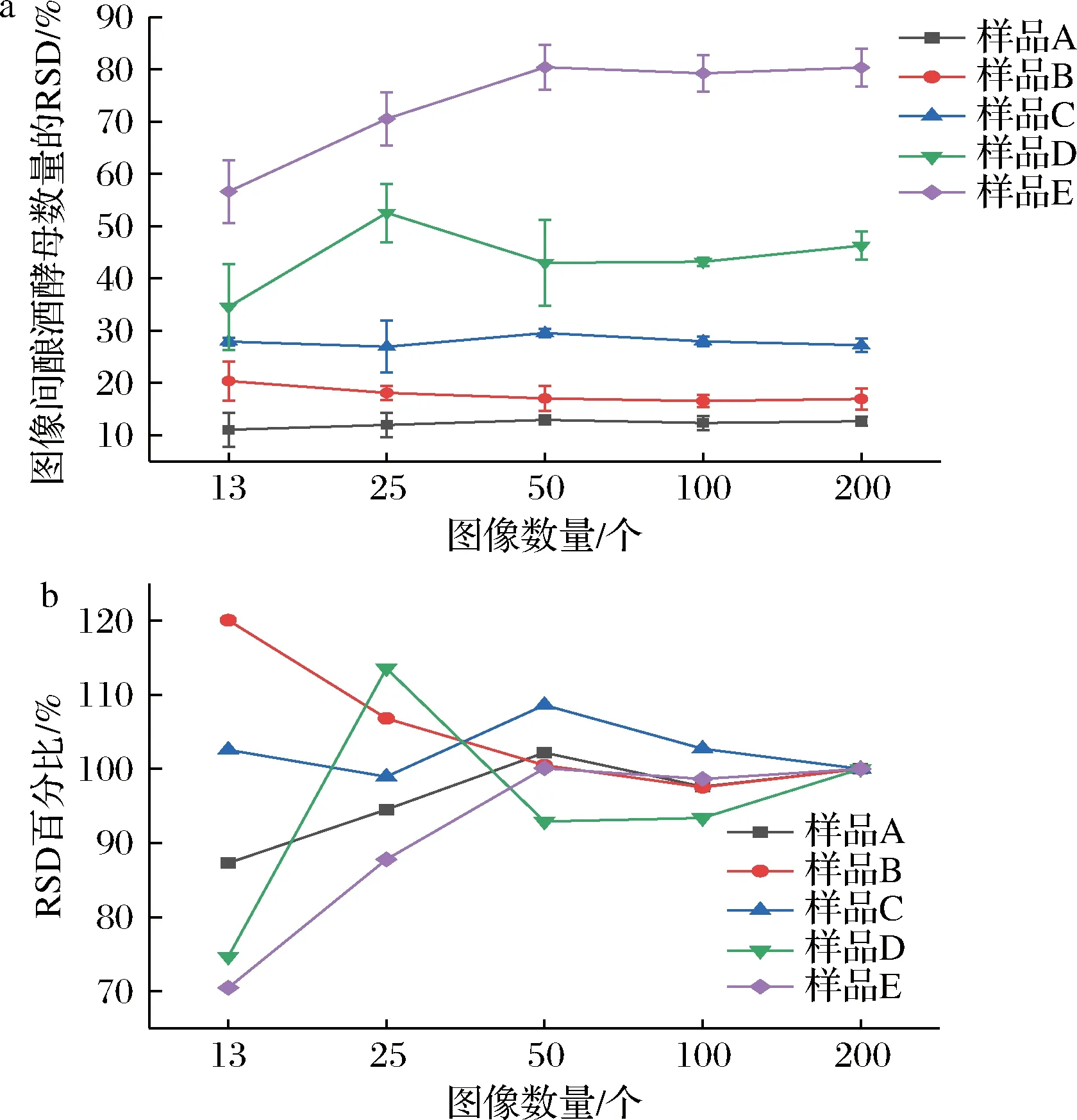
2.3 图像计数与平板计数的对比



3 结论
