柔性网衣结构变形影响因素数值模拟研究❋

曹学睿, 马 辉, 徐明林， 刘凯华， 皮君涛, 周 波❋❋

(1. 大连理工大学工程装备结构分析国家重点实验室， 辽宁 大连 116024； 2. 大连理工大学船舶工程学院， 辽宁 大连 116024;3. 港口航道泥沙工程交通行业重点实验室， 江苏 南京 210024; 4. 大连船舶重工集团有限公司， 辽宁 大连 116000)

联合国粮农组织预测，全球鱼类消费总量每年将持续攀升25%以上，鱼类资源面临巨大的压力。因此，转变人类获取鱼类蛋白质方式，大力鼓励发展海水养殖业变得尤为重要[1]。网箱主要由浮架系统，网衣系统和配重系统三部分组成。在复杂的外界环境下，网箱的网衣系统会发生不同程度的变形，改变了鱼类的生存空间，进而影响养殖鱼的生长；变形过大，甚至会导致鱼群密度激增，养殖鱼群缺氧死亡。因此，通过对模型网箱数值模拟计算，进而反应出实际情况下网衣变形影响因素的研究，具有重大的工程应用价值。

在对网箱的研究中，由于网衣属于小尺度结构物，容易受环境因素影响，产生较大变形，所以对网衣系统的研究是最关键也是困难的部分。为了攻克此难题，国内外对此都投入了大量的研究。Aarnses等[2]较早地对柔性渔网计算变形和受力分布的方法进行研究，将网衣简化为二维平面单元，再将网衣离散为若干平面线单元，忽略了网衣系统的三维效应，并提出了网衣数值模拟计算方法。Lader等[3]通过将网衣假定为由非线性弹簧连接的微元网片组成的柔性体，通过模拟数值分析方法来研究水流作用下，圆形网衣的受力和单纯波浪作用下的平面网衣的受力,并将结果同实验结果进行比对,并发现二者有一定差异,此时仿真模拟网衣系统的一些数值分析方法仍不成熟。李玉成等[4]通过分析与试验相结合的方法分析了田内相似和重力式相似准则，推出了重力相似准则在网衣模型设计中的质量矫正公式及刚度矫正公式。赵云鹏等[5]利用集中质量法建立网衣的数值模型，将不同配重对网衣变形的影响进行了模拟，为不同配重条件下对网衣变形影响因素奠定了基础。

针对目前大多数研究都只停留在对网衣结构变形整体分析，没有定量分析网衣变形程度，且对网衣变形影响因素方面的研究较为薄弱，本文引用体积剩余系数定量分析网衣变形程度，利用Orcaflex软件对网衣结构变形情况的进行研究，根据体积剩余系数的大小判断网衣变形程度的好坏，探讨影响网衣变形的主要影响因素以及影响程度，通过模型尺度网箱延伸到实际尺度网箱得到网衣变形的通用规律，使计算有实际应用价值，从而解决网衣变形导致养殖网箱内鱼类生存空间变小从而影响鱼的生长。

1 理论部分

1.1 网箱整体受力

对重力式网箱进行数值分析，最重要就是对网衣的模拟，由于实际网衣的网目数实在太多，采用直接的模拟方法十分耗时且没有太大意义。因此，为了能将网衣的计算应用到工程实践中，应采用网目群化方法[6-7]。使用此方法需要遵从群化前后的网衣质量、网目所覆盖的面积以及网目沿流速方向的投影面积相等的原则，由此可得，实际网目大小与群化后的网目大小由式(1)表示。

(1)

式中：Sn为网衣实际面积与其投影面积之比；dw为网格中单根网线的外径；lw表示单根网线的长度。

在网衣系统受力方面一般遵循以下假定准则：网衣系统是由有限个无质量弹簧链接的集中质量点构成，构成网衣的网线绝对柔软;网线只承受张力的作用，张力大小是个常数，作用方向在网线轴线上。由于网线属于小尺度构件，其直径远远小于海域中常见波波长，因此可以用Morison方程描述其水动力特性。 Morison方程是个半经验半理论公式，其表达式为：

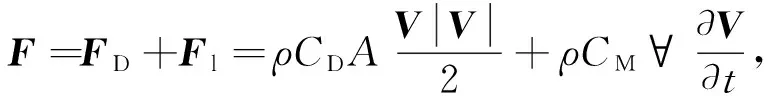
(2)

式中：FD为速度力；Fl为惯性力；ρ为流体密度；CD为速度力系数；A为构件在流速方向的投影面积；V为波流场速度；CM为惯性力系数；∀为构件体积；Cm为附加质量力系数。

1.2 网衣变形计算公式

对于定量分析网箱变形问题，目前最著名的方法就是“切面包法”[6]以及Lader[8]的九点空间坐标法

在文献[7]中，作者选取了网箱上的9个空间坐标点，其编号分别为01、03、05、21、23、25、41、43、45，并在试验中追踪记录这9个点的空间坐标(见图 1)。

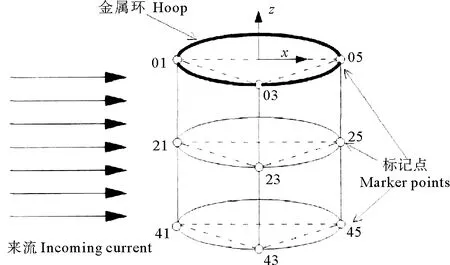
图1 网圆柱上跟踪点示意图[8]Fig.1 Schematic diagram of tracking points on net cylinder[8]

通过这些9个空间坐标点的三位坐标可以求出上下2个三棱柱的体积，相加得网箱空间体积Vp：

(3)

式中：An1,n3,n5为由点n1、n2、n3所构成三角形面积；Zn为i点的z坐标值。由式(3)求出网箱体积可求得体积剩余系数Cvh。

本文基于上述思路将网箱同样分为9个点(见图2)。坐标点编号分别为01、02、03、11、12、13、21、22、23，并跟据各点的三维空间坐标(xij,yij,zij)体系，计算剩余系数Cvh：

(4)

式中Vp0表示在流速为0 m/s，即没有流速情况下的网箱体积，又称初始体积。

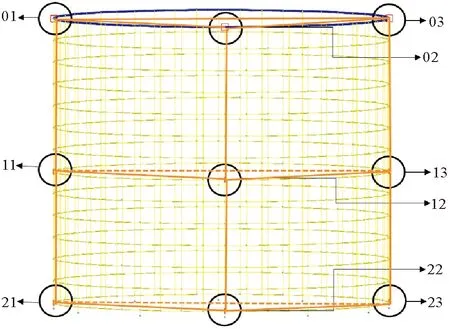
图2 网箱九点示意图Fig.2 Nine-point schematic diagram of cage

2 数值模型

本文主要利用商业软件Orcaflex进行数值模拟分析。在Orcaflex中，可以通过加载非线性阻力载荷计算因流场变化所导致的阻力系数、模型位移等参数，采用此软件对网箱和网衣进行数值模拟有很好的效果。网箱结构主要由浮架系统、网衣系统和配重系统组成。在Orcaflex中，利用line模块来模拟浮架和网衣，此模块是一种无质量弹簧，当模块被赋予质量时，赋予的质量将集中分布在两端，其水动力系数在各运动方向上是恒定的，可以看作为圆柱形杆件，因此用此模块可以等效于使用集中质量法[5]。对于浮架系统，利用6D buoys模块和line依次相连进行模拟，通过6D buoys旋转平移可以表达浮架材料的抗压程度，这种抗压特性在规则和不规则波作用下都是重要的参数。尽管buoys模块链接2个line单元，但并不包涵任何惯性或阻力载荷。在网箱底部，使用若干个带有体积和质量的小圆柱来表示重力式网箱的配重系统。

对于网衣的湿质量部分而言，一般通过调整各网绳链接处3D buoys的质量来模拟始终增加质量部分。为了模拟工程中网箱的实际尺寸大小，网衣直径和长度通过网目群化方法将直径为0.6 mm、长度为6 mm的物理网箱模型等效为直径为14 mm、长度为98 mm的数值模型。最终的网衣数值模拟模型如图3所示。

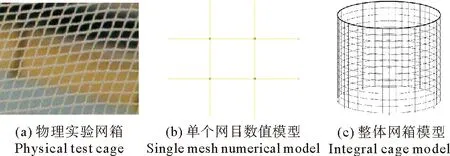
图3 网箱数值模拟示意图Fig.3 Schematic diagram of cage numerical simulation

由于网箱背流侧网衣受到的水流作用是经过上侧水流作用后得到的，所以两侧水流不同会引起两侧的阻力系数不同，对此，通常使用变阻力系数进行数值模拟。阻力系数是莫里森方程中的一个关键分量，所以必须根据不同雷诺数仔细选择。在Orcaflex软件中可以根据雷诺数的变化，计算出不同位置处的网衣阻力系数。在文献[9]中给出了不同雷诺数情况下的阻力系数的计算公式：

(5)

对于重力式网箱的系泊系统，为了能够对数值模拟计算结果进行验证，本文基于Kristiansen和Faltinsen[10]的试验与数值计算模型，采用相同的系泊系统，使用同尺度的流和浪的环境载荷，建立相似的数值计算模型。最终建立的模型如图4-6所示，模型底部是对称分布在网箱底部一周的16个带有质量的3D buoys，用来模拟配重沉子。系泊系统参考Kristiansen和Faltinsen[10]的模型布置，模型共使用了692个buoys以及1 376个line单元。为了保证所得数值模型与Kristiansen的试验模型满足几何相似，本文根据田内相似准则，对line质量、投影面积和缩结面积等参数进行了调整。所建网箱模型的参数如表1所示。

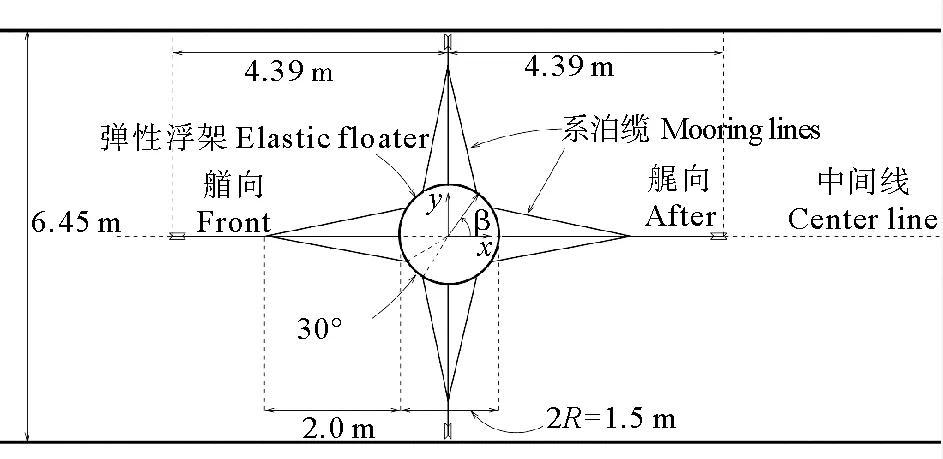
图4 Kristiansen试验模型俯视图[10]Fig.4 Top view of Kristiansen test model[10]

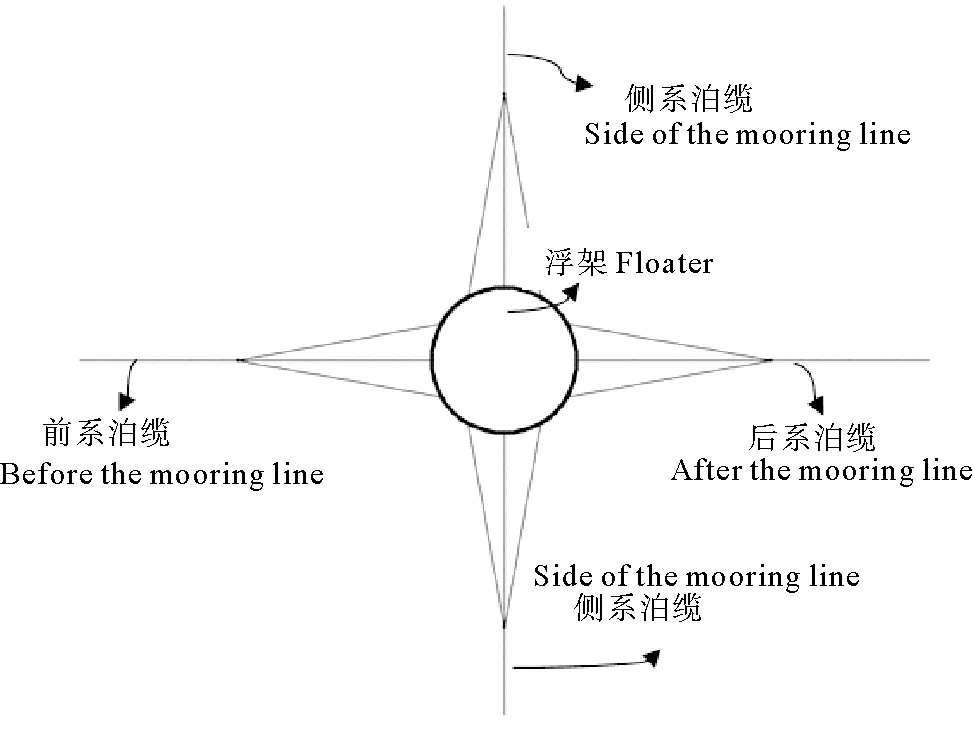
图5 数值模型俯视图Fig.5 Top view of numerical model

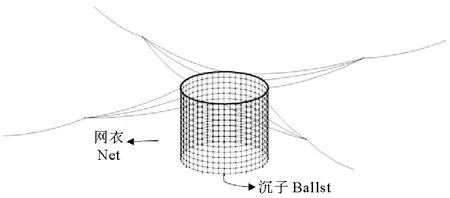
图6 数值模型透视图Fig.6 Numerical model perspective

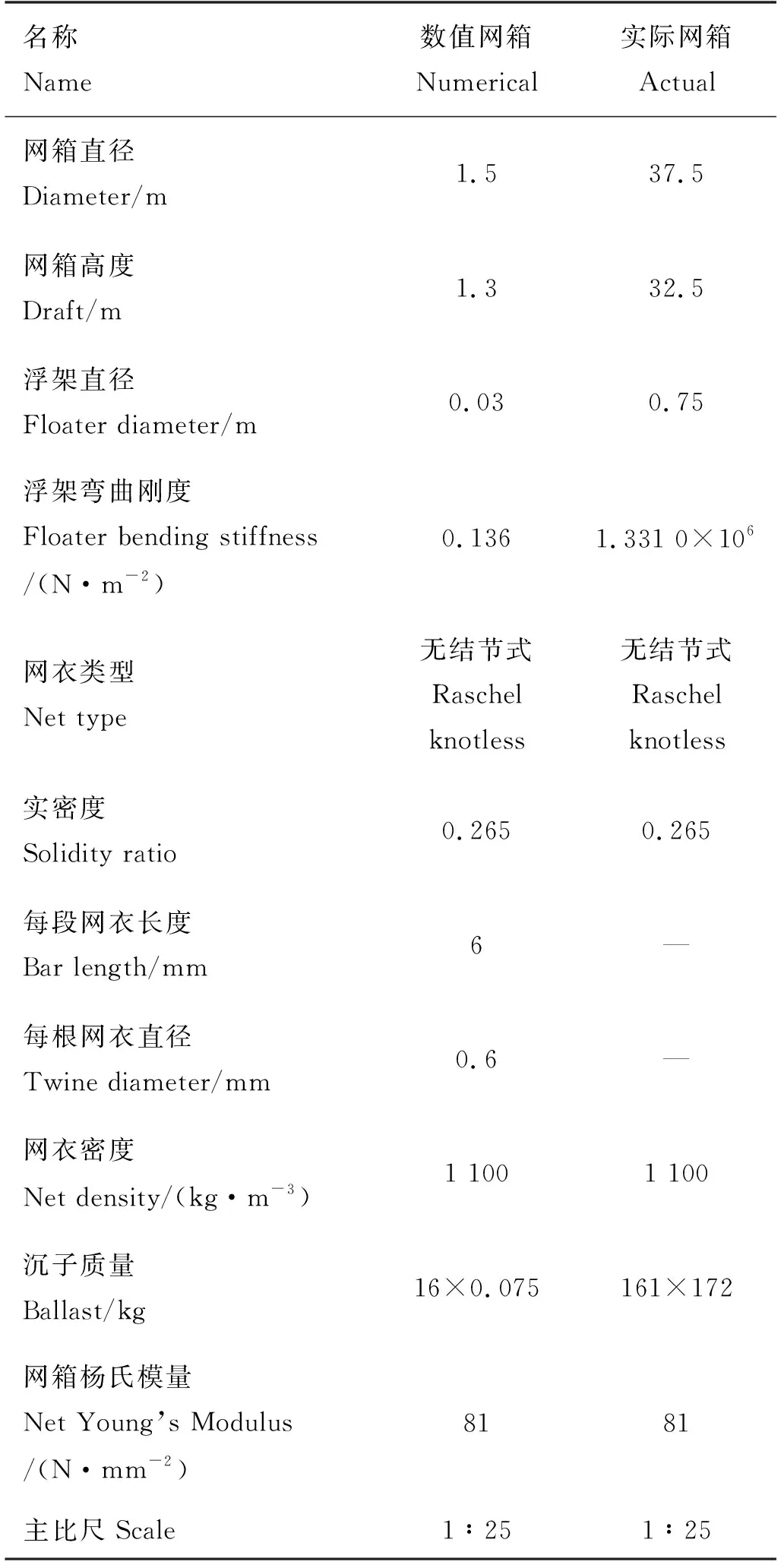
表1 质量式网箱模型参数Table 1 Weight cage model parameters

3 数值计算

3.1 数值结果验证

(1)网箱系泊力验证

将水流看作为流速恒定、流向不变的理想流体，流向为0°表示其平行于前、后系泊缆。由于侧系泊缆会分担前、后系泊缆张力，所以有侧系泊缆网箱的系泊张力略小于无侧系泊缆网箱的系泊张力。为了贴合实际，在数值模拟中加入了侧系泊缆，考虑侧系泊缆对网箱阻力的影响，并根据计算结果绘制了阻力曲线。数值计算结果与Kristiansen等[10]的试验和Cristian等[11]的数值模拟结果进行比较，如图7所示。

此曲线共包含30个数值模拟工况，从最低流速0.02 m/s到最高流速0.32 m/s，相邻工况之间相差0.01 m/s，对应的实际流速为0.1～1.6 m/s。由图4中的曲线可以看出，本文的数值模拟结果与Kristiansen等[10]的试验结果更加接近，更为准确，尤其在高流速情况下，更优于Cristian等[11]的数值计算结果。从而，验证了本文数值计算结果的准确性以及优越性。

为了更好的贴合实际情况，将验证后的数值模型等比例放大25倍，转化为实际尺寸的模型，并根据实际流速0.1～1.6 m/s计算网箱系泊缆张力大小，将该数值结果同根据比例尺放大试验结果Kristiansen等[10]所对应的实际结果相比较得到如图8所示曲线。

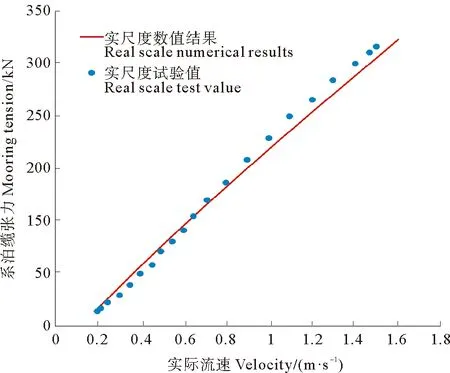
图8 模型尺度网箱放大与实尺度网箱数值对比Fig.8 Numerical comparison between model scale cage magnification and real scale cage

如图8所示，实尺度的数值模拟曲线可以较好的拟合Kristiansen等[10]物理模型所对应的实尺度网箱，因此，此实比例尺的数值网箱可以较好的模拟实际情况，具有实际工程意义。

图9、10分别表示流速为0.1和0.2 m/s的情况下，网箱试验变形与数值变形程度的视觉验证，数值变形同试验变形贴合较好，并且数值变形可以更清晰的描述网衣上方变形情况。

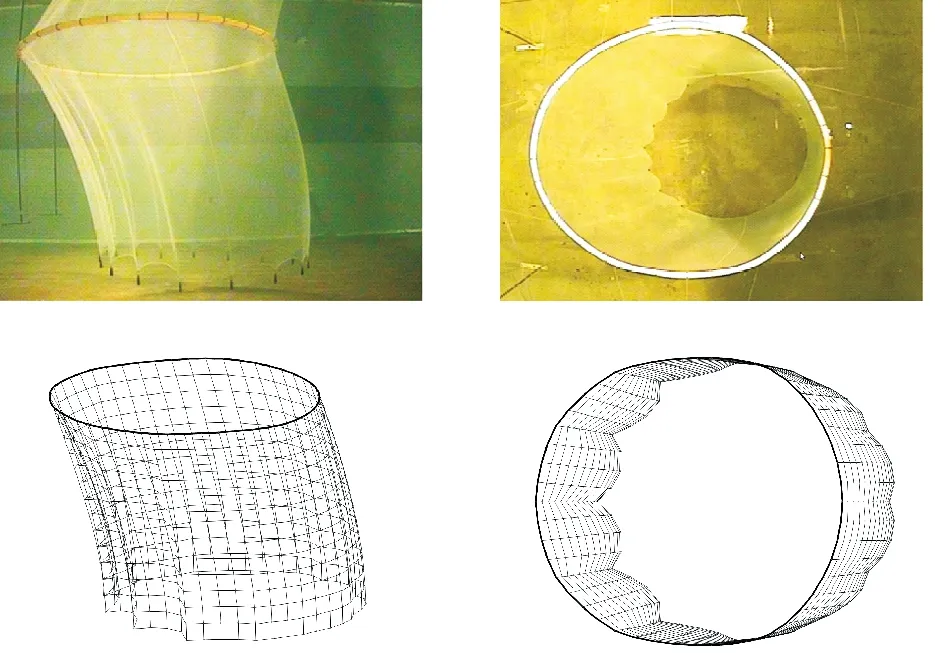
(第一排为试验中所拍得到的照片[10]，第二排为数值模拟得到的示意图。The first row is the photos taken in the experiment, and the second row is the schematic diagram obtained by numerical simulation.)

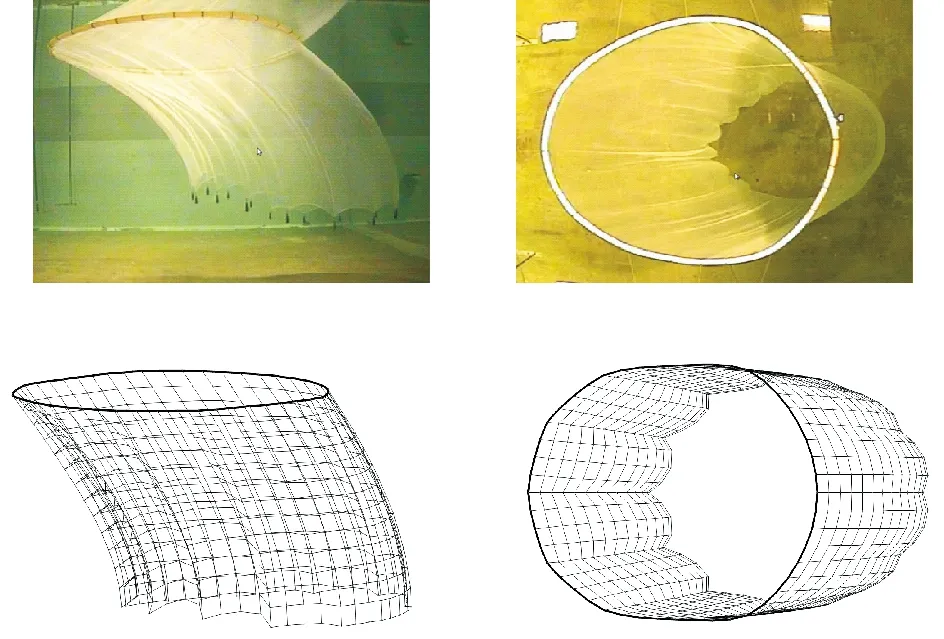
(第一排为试验中所拍得到的照片[10]，第二排为数值模拟得到的示意图。The first row is the photos taken in the experiment, and the second row is the schematic diagram obtained by numerical simulation.)

3.2 流速对网衣变形的影响

因此，此类数值模型可以较好的描述网衣变形情况，为此，图11、12整理了流速从 0.02～0.32 m/s的网衣变形情况。图13所表示，将网箱放置在流速范围在0.02～0.32 m/s的流场内，利用九点坐标法计算网箱的体积剩余系数，并绘制体积剩余系数流速变化曲线。

由图11、12可以看出，流速对网衣变形大小有着重要影响，在流速为0.02 m/s时，网箱体积剩余系数高达0.997，几乎没有发生变形；但在流速达到0.3 m/s时，网箱体积剩余系数可达0.653，网衣变形十分严重，因此可以根据图13体积剩余系数与流速变化曲线可以看出，网衣随流速的增加而变形严重。

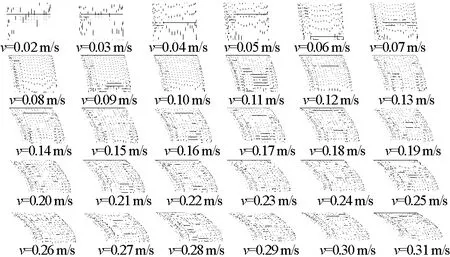
图11 流速在0.02～0.32 m/s的网衣变形正视图Fig.11 Front view of mesh deformation between 0.02 m/s and 0.32 m/s flow rate

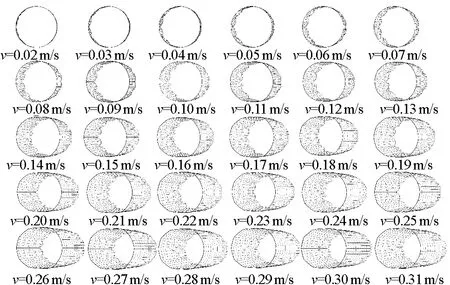
图12 流速在0.02～0.32 m/s的网衣变形俯视图Fig.12 Top view of mesh deformation between 0.02 m/s and 0.32 m/s flow rate

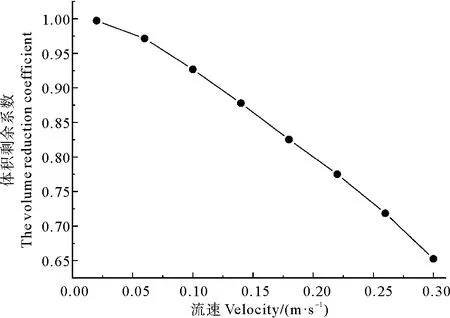
图13 体积剩余系数变化曲线Fig.13 Volumetric residual coefficient variation curve

3.3 网衣变形影响因素

网衣的体积变形不仅跟流速的大小有关，同时配重系统对其也有着不可忽略的作用。配重系统一般直接或间接悬挂于网箱底部，是重力式网箱保持有效容积的重要手段，因此研究配重系统有十分重要的意义。目前比较常用的配重系统分为两种形式：若干沉子单独悬挂网箱底部；网箱底部由一圈带有一定质量的圆形或菱形的底圈构成。

配重系统的选取应在合理的质量区间，过轻或者过重都会造成不利的影响，过轻会导致网箱在水流的作用下有效容积损失过大，不利于网箱内鱼类的生长；过重会导致网线的加粗，从而增加网箱生产成本，同时也不便于管理。所以，通过研究沉子质量对网衣变形的影响，有利于找到最合适的沉子质量。在流速为0.3 m/s时，单个沉子质量分别为55、75和95 g(每种工况下的沉子个数均为16)时网衣体积变形如图14所示。

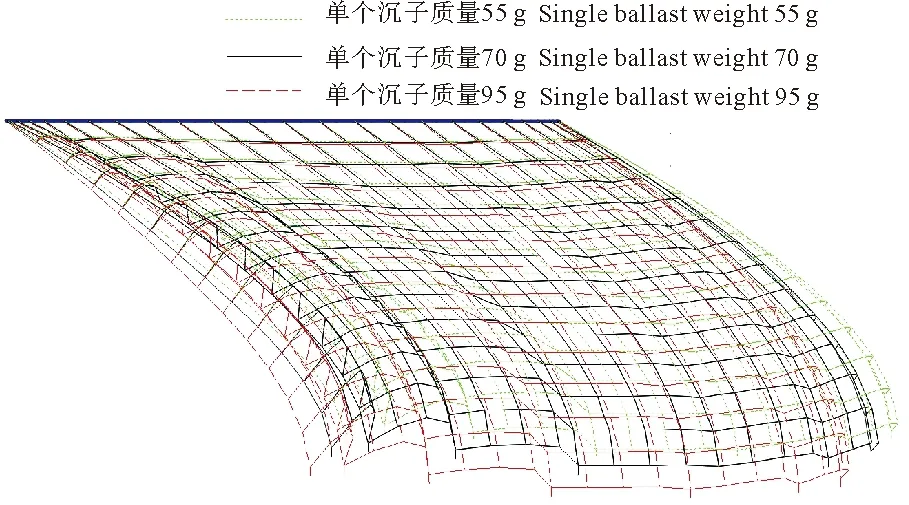
图14 恒定流速下，不同配重网衣变形Fig.14 At constant flow rate, mesh clothing with different weight deforms

由图14可以看出，在相同流速的情况下，配重对网衣变形有着重要影响。在该网箱模拟中，采用了8种设计流速(0.02～0.3 m/s)，按照相似准则对应的实际水流速度范围为0.1～1.5 m/s，取9种配重大小范围为：55～95 g，则图15表示各沉子质量在不同流速下网箱体积剩余系数。

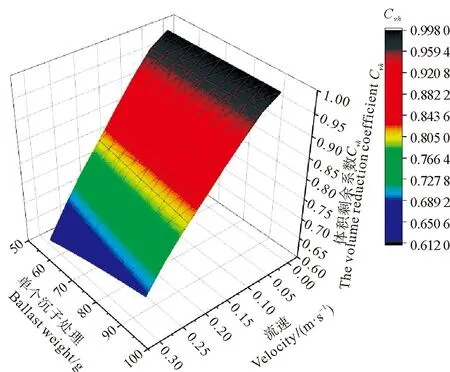
图15 不同沉子质量在不同流速下网箱剩余系数Fig.15 Residual coefficient of cage at different flow rates with different sink masses

由计算结果可知，固定流速，剩余体积系数会随配重的增加而增加；相同配重的情况下，体积剩余系数会随流速的增大而减小。在高流速情况下，配重对网衣变形有更大的影响：在流速为0.3 m/s时，55 g配重情况下的网箱体积剩余系数为0.612，95 g配重情况下的网箱体积剩余系数为0.684，95 g配重时的网箱体积剩余系数比55 g配重时的网箱体积剩余系数增加了11.76%；而在流速为0.02 m/s时，配重变化对网衣变形的影响微乎其微。图16可以看出，体积剩余系数随沉子质量变化曲线弯曲程度。

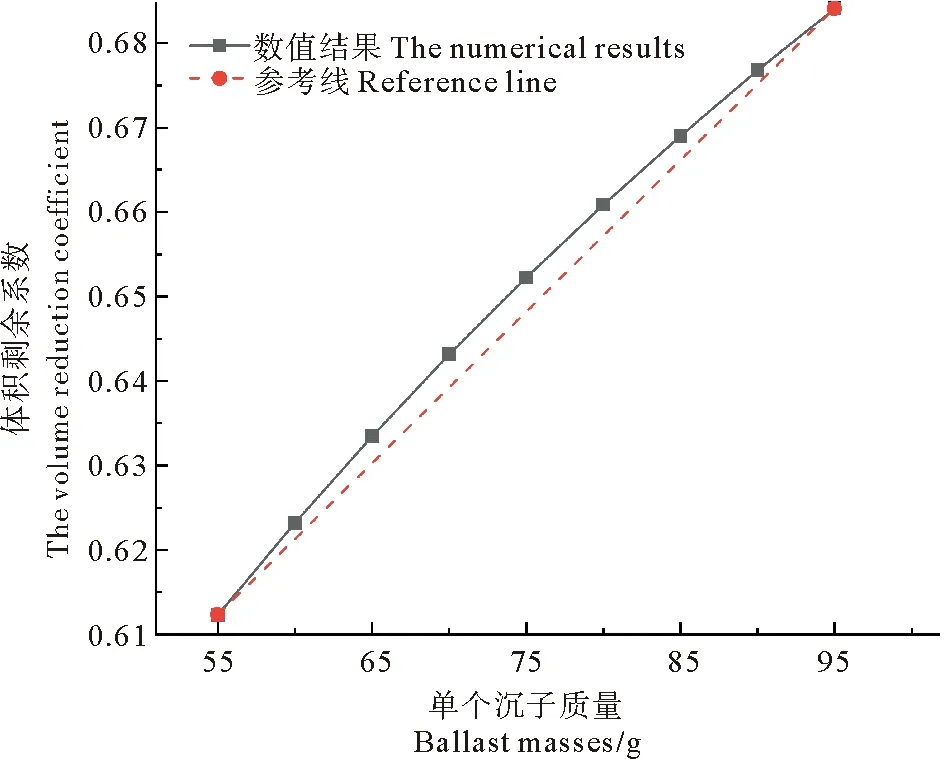
图16 高流速下沉子质量的影响Fig.16 Influence of submergence weight at high flow velocity

由图16可以看出，在高流速如0.3 m/s，沉子质量范围在55～75 g情况下，沉子质量的增加对体积系数影响较大，当沉子质量大于75 g时，沉子质量对体积系数的影响开始减少，所以此网箱系统选择75 g沉子质量最合适,根据弗劳德准则，实际网箱应选择沉子质量为1 172 kg的配重系统。

4 结论

本文基于Orcaflex软件对单一重力式网箱进行了数值模拟分析，将计算得到的纯流条件下系泊缆张力与Kristiansen试验[10]和Cristian数值模拟结果进行比较，验证了数值模拟的准确性，并且在高流速情况下优于Cristian所做的数值模拟。针对水流条件下网衣变形情况，基于九点空间坐标法计算了网箱体积剩余系数，定量分析了网衣随流速以及配重变化的变形程度。经过数值模拟，得出以下结论：

(1)流速对网衣变形有较大影响：在较低流速如0.02 m/s情况下，体积剩余系数可达0.997，网衣基本不发生变形；随着流速的增加，网衣变形程度愈发明显，在流速高达0.3 m/s的情况下，体积剩余系数可达0.653，网衣变形严重。因此可以得出，流速大小对网衣变形程度有重要影响。

(2)在相同流速情况下：配重系统越重，体积剩余系数越大，流速越高，配重系统对网箱变形程度的影响越大；在流速为0.3 m/s的情况下，55 g配重工况下的体积系数为0.612，95 g配重工况下的体积剩余系数为0.684，95 g配重工况下的体积剩余系数比16×55 g配重工况下的体积剩余系数增加了11.76%；而在低流速情况下，配重系统对网衣变形程度的影响较小。但配重并非越重越好，会影响经济效益，因此对于沉子质量的选择，应综合考虑经济性和沉子对网衣变形的影响。针对本文研究的直径为37.5 m、高度为32.5 m的网箱，最佳的配重质量为1 172 kg。