大直径长桥桩钢护筒贯入施工参数优化研究

2023-02-20彭明刚黄顺佩杜长铃郭运华黄文旭

水利水电快报 2023年2期

彭明刚，黄顺佩，杜长铃，郭运华，甘鑫，黄文旭

(1.中电建铁路建设投资集团有限公司，北京 100044； 2.中国水利水电第七工程局有限公司，四川成都 611730； 3.武汉理工大学土木与建筑学院，湖北武汉 430070)

0 引言

中国沿海城市的人口及经济约占全国比重的60%～70%，也是软土分布较广的区域。随着这些城市交通的大规模建设，常常遇到软土地层大直径桩基施工对近接已建工程的扰动问题。研究桩基钢护筒振动下沉施工对近接地铁隧道的影响及施工控制方法，对揭示桩基施工对周边环境影响的规律、提高沿海城市市政设施建设技术水平意义重大。

目前学者对类似问题的研究主要围绕灌注桩钢套管高频振动贯入机理及施工效应。肖勇杰[1]研究了振动频率、动力荷载幅值、接触面摩擦系数和土体模量等参数对施工安全距离的影响，对钢套管高频振动贯入黏性土地基过程中的土塞效应和挤土效应进行了理论计算和数值模拟，并结合试验数据，揭示了套管振动贯入黏性土地基过程中挤土位移和超孔隙水压力的变化规律，分析了土体模量、泊松比、摩擦系数、振动频率和套管直径对挤土位移的影响。秦朝辉[2]通过高频振动下沉钢板桩足尺原位试验和下沉过程数值模拟，研究了钢板桩下沉速率变化特征及下沉作业引起的环境问题。张智梅等[3]进行了PHC管桩数值模拟，发现激振频率与沉桩对环境的影响成负相关，静载力与沉桩对环境的影响成正相关，桩径尺寸的大小与地面振动的相关性不大，主要对地面位移有影响，且砂土场地比黏土场地更易受振动沉桩的影响，土质越硬，沉桩产生的影响越大。刘建鹏[4]通过ABAQUS模拟振动打桩，分析了静载力和激振力与贯入时间的关系。林良庆[5]分析了钢护筒贯入和上拔过程中，管土间摩擦系数、土体杨氏模量、振动锤激振频率等对土体的影响。杨祁[6]研究了高频振动贯入过程中套管内土塞特性及对周围土体的影响，发现高频振动能削弱套管与土体的摩阻力，降低土拱效应的影响，不易形成土塞闭塞，使套管可以贯入更深的土层。倪淯丹[7]使用Plaxis研究了大直径套管贯入过程中套管与土体间的相互作用、沉管后的土体变形情况、超孔隙水压力的分布及沉管对周边环境的影响。张龙等[8]通过ABAQUS建模计算和工程现场监测提出了实际工程条件下近海埋地管道在沉桩振动施工下的安全控制标准，并在实际工程中取得了良好效果。朱福民等[9]提出了一种套筒减振方法，用以将桩与土体浅层隔开，使桩在地下才与土体接触，充分利用土体的几何阻尼和材料阻尼减小地面环境振动。

然而在实际工程中，近地铁处的桩基施工既要考虑地铁的变形，又要保证桩基的下沉贯入。本文结合福州南港道大桥与福州地铁6号线滨海新城站-壶井站区间隧道交汇工程实例，在隧道最小埋深为 4.5 m、与邻近桩基最小间距仅为2.1 m 的情况下，通过有限差分软件FLAC3D模拟钢护筒施工过程，分析了各工况下施工过程对隧道位移的影响，并据此优化施工参数，可为类似工程提供借鉴。

1 工程概况

福州南港道大桥与福州地铁6号线滨海新城站-壶井站区间隧道交汇工程位于福州市长乐区。地铁6号线滨海新城站-壶井站区间盾构隧道直径为6.48 m，最小埋深为4.5 m，地铁隧道与邻近桩基最小间距仅2.1 m。南港道大桥全长105 m，桥宽52 m；桥分左、中、右幅，共有42根桩基，其中中幅桩基18根，左、右幅桩基均为12根。临近地铁隧道的24根桩基采用永久钢护筒，套筒长44～54 m，桩径为1.6，1.8，2.2 m，桩长为65～88 m；其余22根桩基采用临时钢护筒，套筒长6 m，桩径为1.3，1.6，2.2 m，桩长为62～88 m。桥型布置如图1所示。

2 振动下沉荷载计算

采用液压高频振动锤对钢套管进行沉桩施工。总贯入力为Fd。施加在钢套管头端的振动荷载包括2个部分：① 静载力(打桩机配重)F0取300 kN；② 正弦变化的激振力Fv(单位为kN)，最大激振力Fc，其中初始相位为φ0，振动圆频率为ω，如式(1)所示：

Fd=F0+Fv=F0+Fcsin (ωt+φ0)

(1)

根据日本的工程经验[10]，当钢护筒与土相对静止时，管土界面存在静摩阻力。高频振动钢套管将导致界面土体发生液化，摩阻力急剧下降。以Qsv表示高频振动后下降的摩阻力，以μ表示极限静摩阻力Qs变为Qsv时下降的系数，Fmax为液压高频振动锤的最大激振力，则钢护筒贯入所需满足的条件为

Fmax≥Qsv=μQs

(2)

式中：μ根据黄占芳等[10]研究中相关算例取0.2。

钢护筒向下冲击时的振动加速度可由式(3)计算：

(3)

式中：M为当前钢护筒质量，kg；g为重力加速度。其中，M和Qsv大小均与贯入深度h相关。

结合市面上联动型、大型、中型、小型振动锤的性能，分别考虑4 000，2 000，1 000，500 kN的最大激振力输出，计算出各贯入深度阶段振动峰值加速度变化规律，如图2所示。

图1 南港道大桥桥型布置(尺寸单位：cm)Fig.1 Layout of Nangangdao Bridge

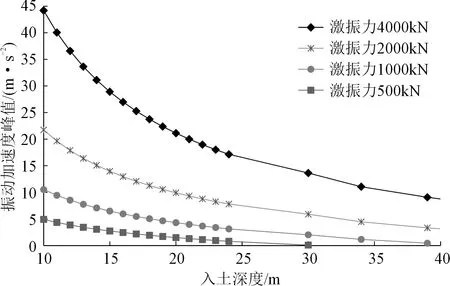
图2 钢套管振动峰值加速度与入土深度关系Fig.2 Relationship between peak vibration acceleration of steel casing and soil depth

从图2中可以看出，在液压振动锤的最大激振力不变的情况下，钢套管振动峰值加速度随着入土深度的增加而呈现减速衰减的变化；根据式(2)，可以确定满足振动下沉条件的最小激振力。为顺利完成振动下沉，本文工程选择联动型或大型振动锤。

3 振动荷载控制

由于本项目需要严格控制近接隧道变形，振动下沉激振力的选择还必须满足冲击导致的地层变形控制要求。因此，采用三维仿真模型研究深厚软土大直径钢护筒振动下沉对既有超近距地铁隧道扰动的影响规律。分析模型的长、宽均取100 m，高为40 m，桩径为2.2 m，隧道直径为6.4 m，埋深为4.5 m。双线隧道中心距为13.2 m。5个桩共线，与隧道走向成20°角。计算模型网格划分如图3所示。

图3 计算模型及网格划分Fig.3 Simulation model and grid division

土体采用finn本构模型，隧道管片采用弹性本构模型。计算参数如表1～2所示。

表2 管片物理力学参数

根据JTG/T F50-2011《公路桥涵施工技术规范》中对钢护筒的规定：钢护筒内径应大于桩径200 mm 以上、高于地面0.3 m，当钢护筒长度大于10 m、需要锤击或振动下沉时，其径厚比不宜大于120，取20 mm。

通过施加钢护筒振动加速度，分析振动下沉对隧道变形的影响，其中加载方式采用加速度动荷载施加方法，即钢护筒模型的所有节点施加相同的加速度，振动锤工作频率取固定值100 s-1。

3.1 钢护筒振动加速度与管片振动速度关系

地铁隧道管片振动安全控制标准为2 cm/s，取钢护筒在隧道轴线高程振动贯入的情况，研究钢护筒振动加速度与管片峰值振动速度的关系，计算结果如图4所示。

计算结果表明：随着钢护筒振动加速度的增大，地铁管片水平峰值振动速度呈减速增长，并最终趋近极限值；垂直峰值振动速度呈加速增长。在该工程的钢护筒峰值振动加速度区间内，管片最大振动速度均在安全范围内；随着振动加速度的增加，振动残余位移增加，岩土振动变形由弹性变形转为塑性变形，最终导致隧道产生永久变形。

3.2 隧道周边最大振动速度与贯入深度关系

根据前述分析结果，选取激振频率100 s-1、峰值振动加速度0.2 m/s2分析隧道周边最大振动速度随贯入深度(以管底低于隧道轴线的距离计)的衰减规律，如图5所示。

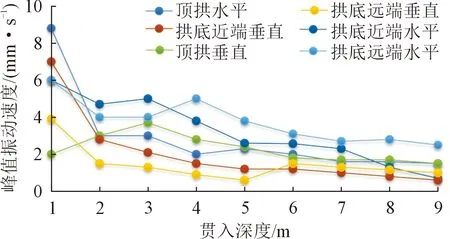
图5 隧道管片振动速度峰值随贯入深度衰减规律Fig.5 Attenuation law of peak vibration velocity of tunnel segment with penetration depth

计算结果表明：除顶拱垂直振动速度峰值出现先增强后衰减的情况外，拱顶水平振动峰值速度、拱底水平振动峰值速度及拱底垂直振动峰值速度均为衰减趋势。根据3.1节分析，顶拱垂直振动峰值速度绝对值为隧道周边振动速度最小值，且随钢护筒峰值加速度增长缓慢，因此在这种情况下，即使出现峰值振动速度增加1倍的情况，振速仍在安全范围内。

3.3 护筒最大振动加速度对隧道周边变形的影响

一般情况下，钢护筒振动峰值加速度最大不超过24 m/s2。分别采用50，28 m/s2及0.2 m/s2的振动加速度计算隧道周边的位移响应。隧道周边位移与钢护筒峰值加速度关系如图6所示。

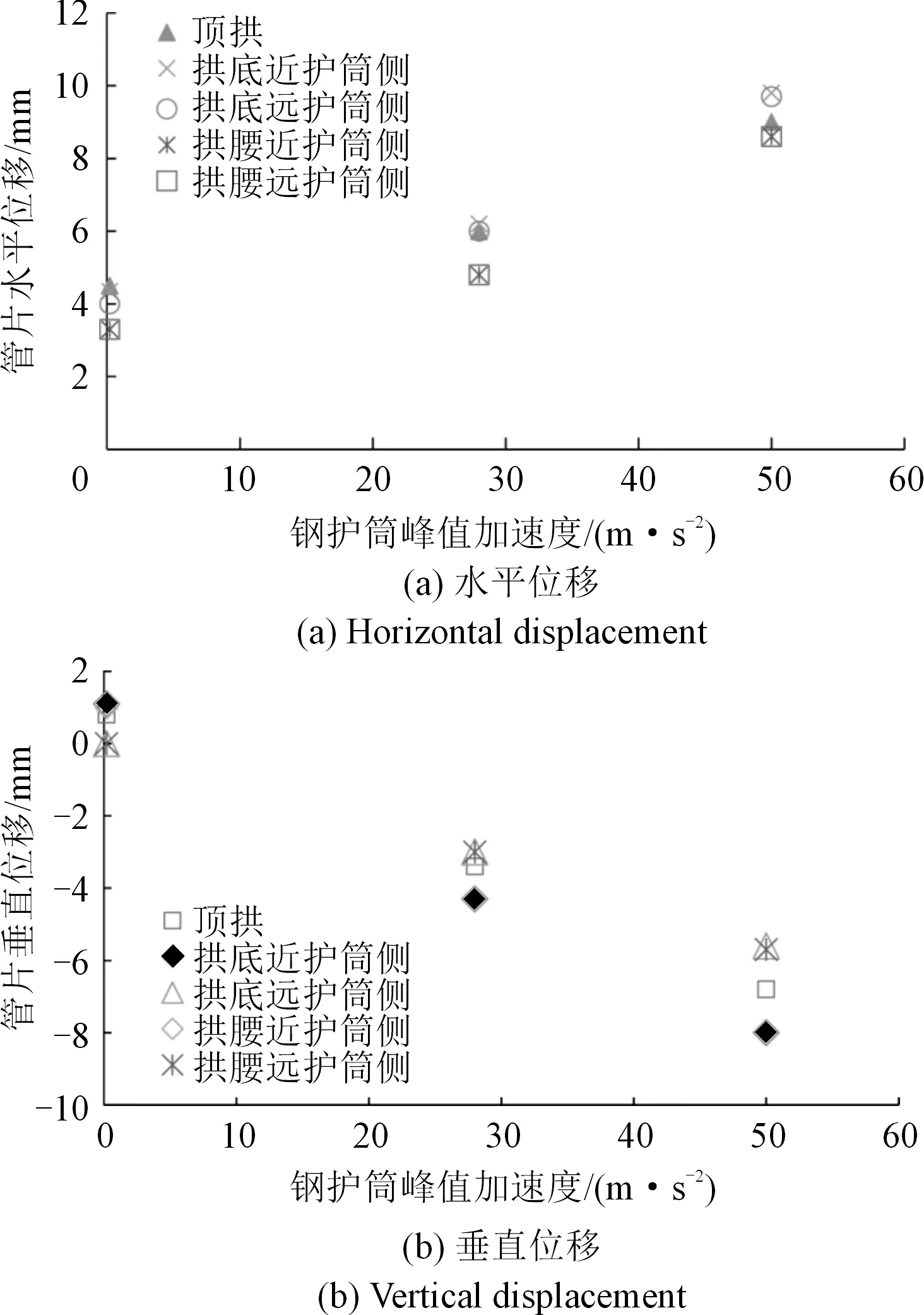
图6 钢护筒加速度与隧道周边位移响应Fig.6 Relationship between acceleration of steel casing and displacement of areas around tunnel

计算结果表明：地铁顶拱、拱底与拱腰处管片的水平位移和垂直位移均随钢护筒振动峰值加速度的增加呈线性增加。其中，各对称部位远近钢护筒侧水平位移基本相对协调变化，但随着钢护筒振动峰值加速度越大，远近钢护筒侧的相对变形协调性越差。因此，控制隧道整体位移与周边变形的关键点在于控制钢套管振动峰值加速度，即控制振动激振力。