非球形气泡的超声定量检测*
2023-02-19张雅婧李凡雷照康王铭浩王成会莫润阳
张雅婧 李凡 雷照康 王铭浩 王成会 莫润阳
(陕西师范大学,陕西省超声学重点实验室,西安 710119)
超声是检测不透明液体中气泡的有效方法,声散射模型是超声反演技术的核心.经典气泡散射模型通常是基于球形假设及ka ≤ 1(a 为气泡半径,k 为入射波的波数),然而实际应用中这些假设并不总能得到满足.本研究针对非球形气泡及ka 偏离假设情况,提出一种超声反演定量方案.建立不受ka 约束的球形气泡级数背散射模型,将其与经典Medwin(ka ≪1)和Anderson(ka≈1)散射模型进行对比,发现ka 偏离引发的散射截面效应仅体现在散射高阶共振峰位置及大小差异上.据此提出:可通过曲线拟合法解决散射截面σbs/(πa2)与ka 间的多值问题,同时用当量半径a* 对非球形气泡尺寸进行量化.具体首先利用非球形气泡背散射信号的频域信息测定其散射截面σbs,再根据σbs 与非球形当量半径a* 间拟合曲线进行反演,同时利用回波时域信息勾画气泡形状轮廓.反演结果通过高速摄影定量结果进行检验.结果表明:气泡沿之字形路径上升过程中产生非球形形变,当9 ≤kr0≤ 35 时,反演得到的非球形气泡当量半径与高速摄影定量半径r0 的相对误差小于45%,对应的最大绝对误差约为1 mm.说明该方法在一定测量精度范围可用于非球形气泡的声反演.
1 引言
液体中气泡在生物应用、渔业科学、工业选矿、纸浆生产及声空化等工程和环境应用中至关重要.如在深水盆地和大陆边缘等地质环境中进行水下甲烷气体泄漏监测[1,2],工业选矿中利用气泡大小分布监测浮选过程[3,4],复合材料[5,6]或推进剂[7]生产中对气泡是否混入及气泡含量进行监测以提高质量;造纸工序中O2泡大小分布是决定纸浆脱木素环节是否顺利进行的关键[8].
气泡表征常用方法有光学和声学两类.光学方法如高速摄影[9]、粒子图像测速系统[10](particle image velocimetry,PIV)、Mie 散射[11]等,定量精度高但在光线不充足或血液、深海及磁流体等不透明环境中则无能为力.超声作为液体中最佳的信息载体,由气泡引起的声能量衰减、声速变化、目标强度和散射截面等均与气泡尺寸和数量等信息直接相关.Ren等[12]设计了脉冲超声和双光纤探头组合测量系统,利用声衰减测量气泡直径,并对三相流中气泡含量进行定量研究.Leighton等[1]通过测量气泡引起的声速变化,对水下沉积物表面气泡大小分布进行量化.Padilla等[13]实验建立了水下气体通量与声背散射强度之间的关系,对南加州海岸圣巴巴拉海峡油田天然气的通量进行评估,并对该区天然气分布予以描绘.
利用声散射信息反演气泡大小的技术,大都基于气泡散射解析模型.较为经典的散射模型主要有Anderson 模型、Medwin 模型、Ainslie-Leighton模型和Yeh 模型[14]等,每个模型都是在一套特定假设条件下的数学表达.散射不仅是入射声波频率和泡内外介质特性的函数,而且要求泡形状为球形,尺寸需满足特定假设条件,若a为气泡半径,k为入射波的波数,Medwin 模型[15]假设ka ≪1,Anderson 模型[16]假设ka≈1.然而,这些基于气泡形状为球形的假设使得这些模型对非球形气泡难以应用.事实上,超声造影剂气泡半径通常在0.5—5 µm 间,形状通常为球形,而液体介质中的气泡若其半径超过1 mm 则很难保持球形[17].海洋、工业过程最为常见的是半径在1—10 mm 的非球形气泡,而且用于气泡监测的声波频率一般从千赫兹到兆赫兹直接导致ka> 1[14].气泡形状的非球形偏离及测量中ka偏离使得上述经典解析模型在用于气泡特性测量如半径反演时出现偏差.Padilla和Weber[14]研究了非球形变对气泡背散射截面的影响,并对基于Anderson,Medwin,Ainslie-Leighton和Yeh 等经典模型进行对比,发现ka在[0.03,0.5]间模型与实验结果一致性很好,而当ka在[0.5,4.4]范围时理论与实验产生明显差异,原因可能是由于这几种模型受ka远小于1 或近似为1 的假设条件约束.
本研究首先建立不受ka约束的球形气泡级数散射模型,通过与Medwin(ka ≪1)和Anderson(ka≈1)模型对比,分析ka偏离引发的散射截面效应;实验测量水中上升的非球形气泡的背散射信号确定其散射截面,通过散射等价对非球形气泡引入当量半径,同时利用散射级数模型拟合关系对气泡当量半径进行反演.反演结果与高速摄影图像分析结果进行对比,研究非球形气泡超声定量方法.
2 实验装置与测量方法
2.1 实验装置
以管内上升气泡为对象,采用光学和声学两种方法同时进行.高速摄影记录气泡运动过程并分析气泡尺寸、形变及轨迹等特征,以这些数据作为对照组,用以检验超声散射信号反演结果.实验装置如图1 所示,充满水的圆柱形水槽高300 mm,底面直径200 mm,在其底部安插一个橡胶管,管出口处接入一个微型针管并用以向水槽中注入气泡.通过调节针管直径和气体流量等控制气泡大小和初速度,气泡半径远远小于容器半径.同一种针管产生的气泡在出口处具有相同的半径,称为气泡出口半径或气泡初始半径并用r0表示.为研究半径不同气泡的运动,采用9 种不同规格的针管在当气体流量一定时,获得出口半径r0分别为0.5,1.0,1.3,2.5,3.2,4.2,4.5,4.8,5.5 mm 的气泡.

图1 气泡测量装置(1-高速摄影机,2-水槽,3-流量控制阀,4-进气口,5-超声换能器,6-声卡,7-工控机)Fig.1.Bubble measuring device.1-high-speed camera,2-tank,3-flow control valves,4-air inlet,5-ultrasonic transducer,6-sound card,7-controller.
多功能超声信号发射接收卡(型号:SUT2008 0125S,中国科学院)产生电脉冲信号并激励固定在水槽壁上的8 个超声换能器,采集和存储气泡背散射信号(采样频率为100 MHz).以换能器声束中心线所在水平位置为超声测量位置,以气泡离开管口时刻为计时起点.高速摄影机(型号:千眼狼X213,拍摄帧率:1000 帧/秒)安放在水槽左侧方,记录气泡上升过程.
2.2 基本理论
2.2.1 气泡的声散射级数模型
声学反演技术的理论基础是散射模型.球形气泡有多种散射模型,其中以Medwin 模型和Anderson 模型最为常用.Anderson 模型给出泡半径尺寸a与入射声波长λ相近(ka≈1)的球形气泡散射模型,未考虑热阻尼和液体黏性的影响,仅考虑传播距离造成的声能衰减.Medwin 模型综合考虑了传播距离、热阻尼和周围液体黏度对声能量的影响,描述了半径远小于波长(即ka ≪1)球形气泡的声散射.然而,这两个模型中球形假设以及ka≤1 这些限制条件,在很多实际应用需求中并不总是能得以满足.那么,若ka> 1 以及非球形气泡的散射截面,因偏离上述假设所产生的效应以及这些模型的偏离程度是值得研究的问题.为此,首先构建球形泡的声散射级数模型,然后与上述两个模型对比,利用偏离程度调整级数模型,使其能用于非球形上升气泡半径的反演.
如图2 所示,球形气泡半径为a,泡内气体为空气,泡外的介质为水.在幅值为1 的平面波声场中,为求解在泡外任意M点的散射声场,借鉴Anderson[16]模型中入射、散射及透射声波的表达式和边界条件,在以r,θ和φ为坐标变量的球坐标系中,入射波pi沿z轴方向,省略时间因子,则pi展开为

图2 球形气泡散射模型Fig.2.Scattering model of spherical bubble.
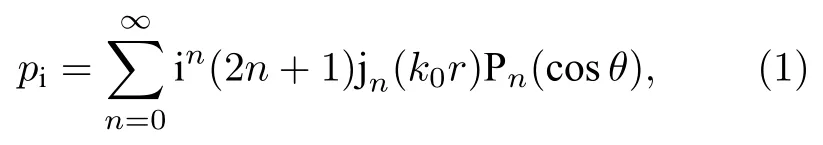
其中k0=ω/c0为水中波数,ω为入射声波角频率,c为水的密度,f为入射声波频率且ω=2πf,n为阶数,jn(k0r)为球贝塞尔函数,Pn(cosθ)为勒让德函数.
泡外散射声压ps可表示为

泡内的透射波声压p1可表示为

其中k1=ω/c1为空气中的波数,c1为空气中声速,bn为待定系数.在r=a处满足边界条件:

将(1)—(3)式代入(4)式和(5)式得散射系数an.考虑到an与气泡形态函数f∞存在关系:

散射截面σbs可表示为[18]

需要注意,利用级数法构建球形气泡散射模型时,忽略热阻尼和液体黏度的影响,因为当入射声波频率远高于气泡的共振频率时,热阻尼和液体黏度对散射的影响很小[19].其次,构建级数模型时仅进行远场近似,且未对ka进行任何限定,故级数模型并不受ka限制.
2.2.2ka偏离引发的散射截面效应
关注ka偏离假设后的效应,将上述3 个模型进行对比.图3(a)和图3(b)给出ka在10—3—1 和1—50 范围内无量纲散射截面(σbs/(πa2))的变化规律.其中蓝色实线表示级数模型,Anderson 模型和Medwin 模型分别用红色虚线和绿色点划线表示.ka≤ 0.1 时(图3(a)),3 条曲线完全重合且具有单值对应性,此时利用散射截面σbs反演泡半径a时3 个模型完全一致;0.1 图3 气泡散射模型对比(a)0.001≤ka≤1;(b)1 ka在1—50 间级数模型和Anderson 模型高阶共振特点见图3(b).ka在1—10 区间,两模型曲线包括稀疏尖峰位置基本重合,说明ka偏离对Anderson 模型影响较小.随ka增大,两者高阶峰均更加密集且位置存在错落,ka偏离产生的散射截面效应主要体现在高阶共振上.ka> 1 后高阶共振峰的出现意味着(σbs/(πa2))-ka单调关系遭到破坏,利用散射截面σbs反演泡半径a则无可能,除非散射波干涉影响可忽略.所幸的是,Sage等[20]在实验中并未观察到高阶共振现象,得到一条近似Anderson 模型的σbs/(πa2)-ka单值关系,认为可忽略高阶共振继续采用Anderson 模型进行反演.事实上,高阶共振未被实验观察到有两种可能:一是散射模型均是基于球形假设,不能分辨气泡的二维形状;另一种可能是,测量中数据点离散恰好与共振点错过.然而,当ka>10 甚至更高为50 时,理论上高阶峰密集程度更高,要使半径反演成为可能须对散射信号进行处理并设法消除高阶影响,具体方法在实验部分3.2.2 节详述.另外,气泡偏离球形假设产生的散射截面效应体现在依据σbs反演出的泡尺寸与实际大小的差距上,同样将在3.2.2 节中进行评价. 3.1.1 上升气泡的形态变化 图4(a)—(c)分别为r0=0.5,1.3 和2.5 mm 的气泡从深度h=120 mm 水下上升时不同时刻的形态变化.在实验过程中,为保证气泡上升条件的一致性,调节气体流量使气泡离开管口时的初速度极小几乎为零,认为所有气泡均从静止开始上升.由图4 可见,气泡刚离开管口时均为球形,上升过程中形态发生了非球形变化,对比发现,r0越小形变越小.通常认为半径在1 mm 内的气泡基本保持球形形状[17],而较大的气泡则难以继续保持球形.上升过程中气泡发生形变,主要归因于泡内外压力差、黏滞阻力和浮力不断变化.另外,出口半径不同的气泡,在上升运动路径中各自的力学过程不同,到达同一水平位置时形态不同,如在图4 中超声测量位置处,3 个气泡在竖直方向上的形状完全不同. 图4 上升气泡的形态变化(h=120 mm)(a)r0=0.5 mm;(b)r0=1.3 mm;(c)r0=2.5 mmFig.4.Shape change of rising bubbles(h=120 mm):(a)r0=0.5 mm;(b)r0=1.3 mm;(c)r0=2.5 mm. 考虑到在测量位置处气泡形态不规则,难以对其大小进行量化评定.为此,将这些非球形气泡近似看作为椭球形,若该椭球与半径为r*的球具有相同体积,则气泡大小可用等效半径r*表示[21]: 其中,m和n分别为椭球的短轴和长轴,χ=n/m为气泡形变率.通过高速摄影所得测量位置处气泡的长轴和短轴,按(7)式对9 种出口半径r0不同气泡,在测量位置处的等效半径r*进行计算,结果见表1. 从表1 可以看出,r0不同的气泡在上升过程中虽然大小形态变化各异,却仍有共同的规律,即到达测量位置时气泡的等效半径r*略大于r0,个别意外可能是测量误差所致,整体上两者差别非常小.这符合力学规律,表明可用等效半径r*对不规则形状气泡进行描述. 表1 测量位置处各泡的等效半径r*Table 1.Equivalent radiusr* of each bubble at the measurement position. 3.1.2 气泡上升轨迹 高速摄影记录了气泡上升全过程,并利用tracker 软件分析其运动轨迹.为便于对比,将追踪软件所得每个泡的轨迹数据重构到一张轨迹图中.以针管出口中心为坐标原点,建立坐标系,其中X表示气泡中心偏离原点O的水平位移,Y表示上升高度.图5(a)和图5(b)分别为r0=4.2 和4.5 mm 两个气泡,从水深h=120 mm(紫实线)和h=160 mm(蓝点线)位置上升的轨迹.由图5(a)和图5(b)可见,气泡上升轨迹呈现“之”字形曲线,水平偏移量与水深h和r0有关.除此之外,水平偏移可能还有一定随机性.图5(c)为r0=4.2 mm两个等大气泡,从同一深度h=160 mm 处上升的轨迹追踪结果.开始时两泡轨迹基本重合,但随着上升高度增大出现水平偏离,两个等大、上升条件完全相同的气泡轨迹偏离表明随机性存在的可能. 图5 气泡“之”字形上升轨迹(a)r0=4.2 mm,h=120,160 mm;(b)r0=4.5 mm,h=120,160 mm;(c)r0=4.2 mm,h=160 mmFig.5.Zigzag rising trajectory of the bubbles:(a)r0=4.2 mm,h=120,160 mm;(b)r0=4.5 mm,h=120,160 mm;(c)r0=4.2 mm,h=160 mm. 气泡上升轨迹发生水平偏移的原因与其形状变化密不可分,而气泡形变则与浮力、黏滞阻力以及泡内外压力差和压差所致的内外气体交换等有关.气泡上升的“之”字形轨迹以及水平偏移量与其出口半径r0和水深h有关.为进一步探究当h一定时水平偏移量与r0间关系.令h=120 mm,图6(a)—(c)为高速摄影直接追踪所获r0=0.5,1.3,2.5 mm三个气泡的运动轨迹.可见,r0=0.5 mm 气泡轨迹近似直线,而后两者出现明显水平偏移.可以推测,r0在1 mm 内的气泡上升过程中非球形变很小、轨迹近乎直线,大泡则一定会发生非球形变. 图6 自同一水深处上升气泡轨迹(h=120 mm)(a)r0=0.5 mm;(b)r0=1.3 mm;(c)r0=2.5 mmFig.6.Rising bubble trajectory with same depth(h=120 mm):(a)r0=0.5 mm;(b)r0=1.3 mm;(c)r0=2.5 mm. 气泡在测量位置处的大小、形状与其运动过程密切相关.气泡散射一般用散射截面σbs或远场背散射声压Pf表示,利用测量位置处气泡的声散射特性,可对其散射截面进行测量,对形状及半径进行反演. 3.2.1 基于时域回波信号幅值的气泡截面形状轮廓 在图7(a)所示圆周每间隔45°采集散射时域信号,整个圆周共计采集8 个信号.图7(b)为在信号采集硬件、参数设置及其他条件完全相同时,r0=1.3 mm 气泡在不同角度测量位置所获散射信号的时域波形图,其中以红、蓝、绿和黑色表示的波形分别对应图7(a)中的1,3,5,7 号换能器,因气泡形状为非球形,在各测量角度所得回波幅值Pfj(j=1,2,···,8)和回波时间tj(j=1,2,···,8)并不相同(图7(b)中虚线对应不同位置处脉冲回波前沿),利用回波到达时间和幅度差异对非球形气泡的水平截面进行描绘. 图7 气泡散射时域信号及采集方法(a)信号采集示意图;(b)不同角度的气泡时域散射信号Fig.7.Time domain scattering signal of bubble and data acquisition method:(a)Schematic diagram of signal acquisition;(b)time domain scattering signals of bubbles at different angles. 勾画泡的水平截面形状时,借用超声无损检测中当量半径概念,即若一个非球形气泡的散射强度与同距离处球形气泡的散射强度相等,则认为该球形泡的半径即为该非球形气泡的当量半径,并用a*表示.换能器在8 个角度采集到的气泡远场回波声压幅值Pfj与其当量半径间关系近似为[22] 其中dj为泡表面到换能器端面的距离且dj=(ctj)/2,水中声速c=1480 m/s,P0为入射波声压,Fs为压电晶片面积,λ为水中声波波长,A是与测量系统相关的系数且对同一套测试系统A为常数,此时Pfj与成线性关系. 具体步骤是,首先将换能器在不同位置处采集到的回波信号幅值Pfj(j=1,2,···,8)和回波时间tj(j=1,2,···,8),按关系式(8)求出其对应的等效半径(j=1,2,···,8),然后分别以为半径、以45°圆心角做8 个圆弧(由于散射信号是间隔45°采集,故取45°为圆心角),最后将这8 段圆弧拼接得到非球形泡的水平截面形状.当然,若信号采集单元更多、圆心角分割更小,则勾画出的水平截面图则更详尽.表2 第1 行为出口半径r0分别为0.5,1.3 和2.5 mm 三个气泡在测量位置处的水平截面形状,三者几乎都为椭圆.为便于全面了解气泡形态,表2 第2 行列出了高速摄影所获泡的竖直面图像.为进一步分析气泡在上升过程中的形变,将气泡在水平面上的形变率用χ*表示,上述3 个气泡的χ*依次为1.2,1.2,1.3,对应于表1 中竖直面上形变率χ分别为1.5,3.2,2.7.可见,气泡在上升过程中的形变主要发生在竖直方向上,水平方向上的形变程度很小,以至于气泡的水平面长短轴之比依然接近1,更接近于圆形. 表2 测量位置处气泡的形状及形变率Table 2.Shape and deformation rate of bubbles at the measurement position. 3.2.2 气泡散射截面σbs测量及当量半径a*反演 用σbs描述气泡散射并通过频域信息对其进行测量.具体步骤是:采集并提取气泡散射时域信号,对其进行傅里叶变换并将结果记为g1(f),如图8(a),提取某一频率所对应的g1,再按(9)式计算气泡散射截面σbs[14]: 其中d为超声换能器端面到气泡表面的距离;α为水中的衰减系数;Cm[23]为图8(b)所示校准因子(具体确定方法见附录A),是一个与气泡大小无关而仅与收发系统、发射信号及泡周围介质有关的常量.实验采用中心频率为4.5 MHz(—6 dB 带宽,2.5—6.5 MHz)的换能器激励和接收散射信号. 图8 频域散射信号(a)和散射截面校准因子(b)Fig.8.Frequency domain scattering signal(a)and calibration factor of scattering cross section(b). 图9 中为实验所测r0=0.5,1.3,2.5,3.2 mm四个气泡对应于各频率点上的散射截面σbs.对比4 条曲线发现,σbs具有频率依赖性;相同频率下,气泡r0越大σbs越大、散射越强.利用σbs进行a*反演时不同频率下所得a*值不同. 图9 -6 dB 带宽范围σbs 测量结果Fig.9.Measurements ofσbs in the —6 dB bandwidth. 为使反演结果更接近实际,需根据气泡尺度合理选择频率或频率范围.在此首先在探头—6 dB 带宽范围(2.5—6.5 MHz),按照100 kHz 间隔逐点对气泡当量半径a*进行反演.在此以f=4.5 MHz为例介绍具体反演过程.图10 黑色点线为按(6)式计算级数模型当f=4.5 MHz 时的σbs-a*曲线,显然因高阶共振影响σbs与a*并非单值对应,在此对该曲线进行二次方拟合且拟合方程为σbs3×10-7a*2-1.1×10-7a*+5.8×10-8m2(红色实线所示),将超声所测σbs=9.7×10—8m2与拟合曲线对照,反演出其当量半径a*=0.6 mm(绿色 所示). 图10 非球形气泡当量反演示意图Fig.10.Inversion schematic for non-spherical bubbles. 图11 给出了上述4 种气泡在探头—6 dB 带宽内a*的反演结果,其中用δ=|a*-r0|/r0表示其与高速摄影测量结果的相对误差.对比r0=1.3,2.5 和3.2 mm 三种气泡发现,r0=1.3 mm时a*偏离r0最小(用绿色表示,18%≤δ≤42%),r0=2.5 mm 次之(用红色表示,35% ≤δ≤ 61%),r0=3.2 mm 偏差最大(用蓝色表示,32%≤δ≤67%).由此可见,气泡初始半径r0越小、a*偏离越小,主要是由于反演的级数模型是建立在球形假设上,气泡越小其形状越接近球形,反之气泡尺寸越大非球形变越严重,理论反演时偏差越大.r0=0.5 mm 的气泡在9 ≤kr0≤ 14 范围内的结果依然表现出和其他3 种气泡相同的规律(用黄色表示),但当5 ≤kr0<9 时却出现反常,这可能是由于小气泡散射较弱使测量结果不准确所致,而且对高速摄影图像处理得到的r0与气泡实际大小也存在误差.从kr0范围上分析发现,9 ≤kr0≤35 范围内,非球形气泡当量半径反演结果与高速摄影定量结果间的相对误差基本可控制在45%以内,另外经计算发现实验中的4 种气泡在这一范围里a*和r0的绝对误差|a*-r0|都基本可以控制在1 mm 以内,这种定量精度在很多工业应用中基本可以满足. 图11 超声与高速摄影定量结果对比Fig.11.Comparison of quantitative results of ultrasound and high-speed camera. 改进了偏离ka≤ 1 假设及发生非球形形变的气泡的散射反演技术,给出了一种基于超声量化评定气泡形状和尺度的方法.建立气泡的散射级数模型解除经典散射模型中ka≤ 1 这一约束条件,同时通过引入当量半径概念对不规则的非球形气泡大小进行定量.对于ka >1时σbs-a曲线出现的高阶共振峰,采用对级数解进行二次拟合的方法进行消除并将拟合曲线用于非球形气泡当量半径的反演.在9 ≤ka≤ 35 范围,该方法在对实验所用出口半径分别为0.5,1.3,2.5,3.2 mm 气泡的测量中,非球形气泡当量半径反演结果与高速摄影定量结果间的绝对误差基本可控制在1 mm 以内,相对误差可控制在45%以内.此外,还根据时域回波信号勾画出了非球形气泡的水平切面轮廓. 附录A 校准因子Cm的确定方法 校准因子Cm[23]是一个与探头频率、发射信号类型及泡所处的液体介质有关的量,和所测气泡半径并无直接关系,因此在Cm确定中可任意选择某一尺度的气泡进行.在此任选出口半径r0=1.0 mm 气泡确定Cm(f).由于气泡上升过程中的形变和水平偏移具有随机性,故通过对8 组数据求平均的方式来降低这种随机性的影响.
3 结果与讨论
3.1 高速摄影-气泡形态和运动轨迹分析

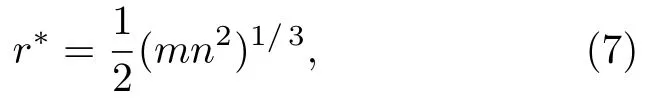



3.2 运动气泡高频超声检测
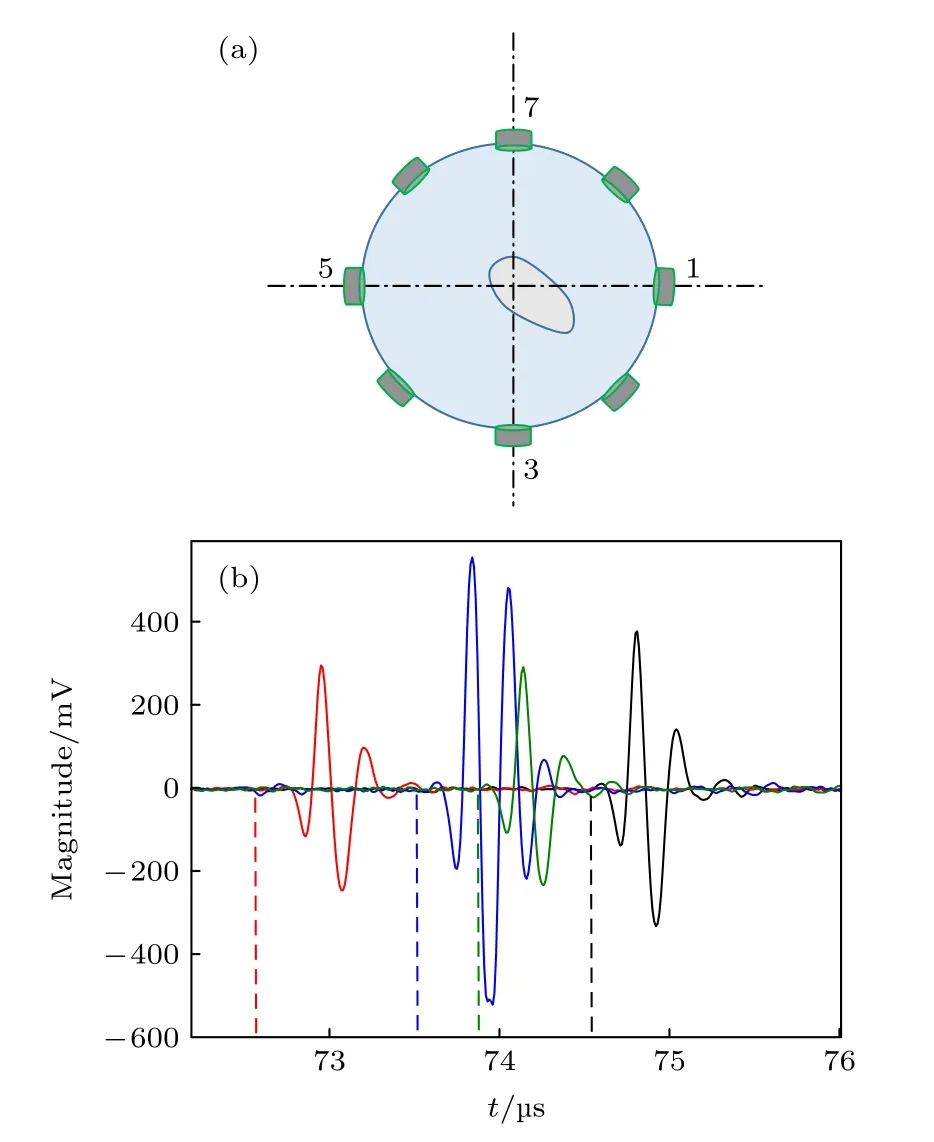






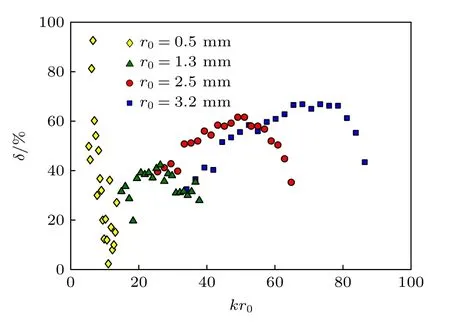
4 结论

