基于一种近邻传播的多目标分布估计算法

傅红宇

(重庆邮电大学 自动化学院，重庆 400065)

0 引言

目前，多目标优化问题(Multi-objective Optimization Problem，MOP)已出现在众多工程领域，与传统单目标优化问题不同，MOP中存在多个相互冲突的目标，如何获得所有目标的最优解，一直是学术领域和工程领域关注的焦点[1]。自1985年Scahffer[2]首次提出求解MOP的算法——基于矢量评价遗传算法 (Vector Evaluated Genetic Algorithm，VEGA)以来，众多的多目标优化算法也相继被提出。

分布估计算法(Estimation of Distribution Algorithm，EDA)是众多优化算法中的一种[3]，因其亮眼的表现，也被应用于MOP[4]。与传统的优化算法相比，EDA没有交叉和变异操作，而是通过提取全局统计信息来建立概率分布模型，然后采样生成新的解决方案。

在一定的平滑情况下，根据Karush-Kuhn-Tucker条件，连续MOP的中帕累托解集PS是一个(m-1)维的分段连续的流形[5]，其中m为目标函数的个数。基于此，Zhang等[5]于2008年提出基于规则模型的多目标分布估计算法(Regularity Model-based Multio-bjective Estimation of Distribution Algorithm，RM-MEDA)来解决MOP。在RM-MEDA中，采用LPCA算法建立K个概率模型来分别描述子种群的分布信息，然后采样生成新个体。同时，RM-MEDA也存在以下不足：① 该算法的全局搜索能力较弱，从而影响了算法的收敛速度；② 概率模型的准确性依赖于聚类数目K值，具体问题的K值是不尽相同的，预设的K值过大或过小，都将影响概率模型的准确性，从而影响算法的性能。

针对RM-MEDA全局搜索能力较弱的问题，许多学者通过引入全局搜索能力强的多目标优化算法与之结合，在一定程度上提高了算法的性能。王剑文[6]通过判断种群是否收敛来自适应地选择遗传操作或者建模采样操作来生成下一代种群，提高了算法的收敛性。向健[7]将差分变异算子与RM-MEDA相结合，混合产生新的个体，有效提高了全局搜索和局部搜索能力。2019年王惠君[8]在RM-MEDA的基础上，与另一种基于逆模型的连续多目标分布估计算法相结合，自适应地通过2种算法生成新个体，在一定程度上提高了算法的整体性能和解的分布性。

为了降低预设K值对算法性能的影响，当预设的K值大于实际情况时，Wang等[9]提出了一种去冗余聚类算子(RRCO)来修正K值，以此在进化过程中建立更精确的模型，提高了算法的收敛能力。当预设的K值小于实际情况时，无法建立正确的概率模型，从而降低算法的性能，故Shi等[10]提出了去聚类操作，同时结合全变量高斯模型，提高了算法的整体性能。不同问题的PS所构成的流形结构不同，故所需的K值是不尽相同的，如何根据实际问题自动确定K值是研究的重要内容。

基于以上分析，本文提出了一种基于近邻传播(Affinity Propagation，AP)的多目标分布估计算法(AP-RM-MEDA)。针对RM-MEDA中预设的K值可能与实际不符从而导致无法建立准确的概率模型的情况，引入了AP算法来自动确定种群的聚类个数，从而避免人为设置K值的不确定性；考虑到迭代后期种群的数据信息逐渐趋同，提出了一种聚类数目重用策略，根据重用策略来判断是否进行聚类操作或重用之前的聚类结果，在一定程度上减小了聚类操作所带来的计算开销；针对RM-MED全局搜索能力较弱的问题，除根据概率模型采样生成新个体外，还将混合差分变异算子产生部分新的个体，提高了算法的整体性能。

1 问题描述

一个MOP通常由N个决策变量、M个目标和若干约束条件组成[11]，表示如下：

minF(x)=(f1(x),f2(x),…,fM(x))T，

(1)

s.t.x∈Ω

gi(x)≤0;i=1,2,…,p，

(2)

hj(x)=0;j=1,2,…,q，

(3)

式中，x=(x1,x2,…,xM)为M个N维决策变量形成的变量集；fi(x):Rn→R,i=(1,2,…,M)为第i个目标函数；F(x)为M个目标函数组成的目标向量集。式(2)为p个不等式约束条件；式(3)为q个等式约束条件。

大多数情况下，各目标函数之间是相互冲突的，同时使得所有的目标函数达到最优是不太容易实现的，故需要寻得一组均衡解集[12]，即Pareto解集，使得目标函数在满足给定约束条件的情况下尽可能达到最优。

2 AP-RM-MEDA算法

在RM-MEDA算法中，按照预设值，将种群分为K类，并通过PCA算法建立相应的概率模型。但是对于不同的问题，预设的K值并不一定符合实际问题。如果K值设置得过大，对于实际问题的Pareto前沿则显得冗余；如果K值设置得过小，则不能覆盖实际的Pareto前沿，从而无法准确地刻画种群的分布。因此，如何设定合理的K值是一个比较困难的问题。

本文提出的一种AP-RM-MEDA，根据具体的种群数据信息对种群进行聚类，自动确定了种群的聚类数目，从而避免了人为设置K值的不确定性。

2.1 AP聚类

AP算法是Frey等[13]于2007年提出的一种聚类算法。与其他经典聚类算法不同的是，该算法不需要指定聚类数目[14]和初始聚类中心，而是以数据点集合的相似度矩阵作为输入，将所有的数据点作为潜在的聚类中心，通过传递、交换数据点之间的信息来确定聚类中心，从而得到聚类结果。

在AP算法中，传递的信息参数包括吸引度(Responsibility)和归属度(Availability)2种。吸引度r(i,k)代表的是，考虑样本点xi对其他候选类中心点支持程度的情况，数据点xk适合作为xi类中心点的程度。归属度a(i,k)代表的是，考虑其他数据点对xk的支持度的同时，样本点xi选择xk作为其类中心点的适合程度。通过对归属度和吸引度的计算更新，当二者的和稳定不变时，得到聚类结果，计算步骤如下：

① 设置吸引度和归属度的初始值：r(i,k)，a(i,k)均为零。

② 根据式(4)对吸引度进行计算更新：

(4)

式中，s(i,k)表示样本点xi和数据点xk之间的相似度，吸引度r(i,k)的更新使得所有数据点都能成为候选类中心点。

(1)更新归属度

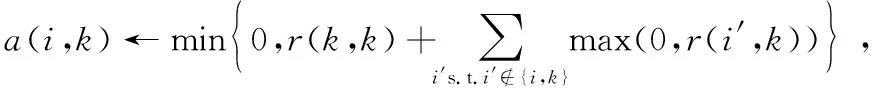
(5)

归属度a(i,k)的更新将确定每个候选类中心点是否是一个好的类中心点。式中，r(k,k)表示数据点xk的自我吸引度。

(2)自我归属度a(k,k)更新

(6)

式(6)反映了基于其他数据点对候选点xk的支持，数据点xk成为类中心点的适合程度。

(3)得到类中心点

对吸引度和归属度进行多次计算更新后，当r(i,k)+a(i,k)连续多次取得最大值k不变时，则表明xk成为当前样本点xi的类中心点。若i=k，表明xi为当前类的类中心点；若i≠k，表明xi属于xk代表的类。

2.2 聚类数目重用策略

为了减小AP聚类操作带来的计算量，在不过多损失聚类结果准确度的前提下，在提出的AP-RM-MEDA算法中，考虑重用聚类数目K值。即如果连续L代的聚类结果都保持不变，表明相邻种群的个体组成差异较小，种群分布信息类似，则直接使用当代聚类数目作为后续种群的聚类数目。具体的实现过程如下：

① 保存历代AP聚类结果K值。

② 判断连续L代的K值是否改变，若保持不变则将该值作为当前及后续进化的聚类数目。

从上述可以看出，该重用机制本身并没有带来额外的计算量。通过后续实验发现，在迭代次数较大的情况下，尤其在算法进化的后期，每代AP聚类结果变化率很小，故这种重用机制在没有过多影响算法的性能下能较好地减小计算开销。

2.3 混合算子

在RM-MEDA中，执行聚类操作后通过LPCA对每一类群体建立对应的概率模型，高斯采样生成新的种群。这种建模操作属于宏观操作，有利于开采种群的统计信息，充分体现了解集在决策空间的分布性，但忽略了个体的特征，不利于勘探搜索空间的不同区域。故考虑引入简单高效的差分变异算子进行搜索[15]，利用个体的信息可以增强算法的性能。由此，通过建模采样和差分变异2种算子混合产生新解，有利于提高RM-MEDA的求解能力。

采用差分变异算子产生新解的过程如下：聚类操作之后，从每类当中随机选择2个个体，组成全局子种群I。然后，随机从全局子种群中选择2个个体作为父个体xr1，xr2，采用差分进化算子产生新解：

x′i=xr+u×(xr1-xr2)+F×(xr1-xr2)，

(7)

式中，xr是从当前种群中随机选择的个体；u为0～1的随机数；xr1，xr2是从全局子种群I中随机选择的互不相同的个体；F为变异因子的缩放参数。

2.4 AP-RM-MEDA算法步骤

根据2.2节中提出的聚类数目重用策略判断是否进行AP聚类操作，然后根据其聚类结果或重用聚类结果分簇建立相应的概率模型，其建模步骤如下：

(8)

式中，Xi为种群第k簇决策向量的集合；n为每簇所包含的个体数量。

② 每簇的协方差矩阵D为：

(9)

③ 根据协方差矩阵计算每簇个体的特征值λi及特征向量a，并根据特征值降序排列，选择前(m-1)个特征向量作为主向量，且由主向量组成向量矩阵A。

④ 将每簇的个体都按照主向量方向进行投影，计算每簇子种群的概率矩阵B：

(10)

对每簇生成的(m-1)个主成分概率模型采样生成新的个体向量，同时为了使个体更加均匀地分布在非支配解集周围，叠加一个均值为0的噪声向量ε：

x′=x+ε，

(11)

式中，x′为新产生的个体；x为采样得到的个体向量。

AP-RM-MRDA算法的完整步骤如下所示。

输入：种群规模NX，决策变量维度DX，最大进化代数MaxIter，决策变量的最大值XUpp及最小值XLow。

输出：算法最终得到的新种群PopX(t)及其目标函数值PopF(t)。

(1)种群的初始化：随机生成初始种群PopX(0)，并计算其目标函数值PopF(0)。

(2)判断算法是否满足停止条件：若t>MaxIter，结束算法并输出结果；否则执行步骤(3)。

(3)根据2.2节聚类数目重用策略判断是否执行AP聚类操作，若不满足条件，根据2.1节执行AP聚类操作，输出聚类结果，执行步骤(4)；若满足条件，则直接重用上一代聚类结果，执行步骤(4)。

(4)通过建模采样方式和差分变异算子共同生成新个体：

① 根据步骤(3)的聚类结果，根据式(8)～式(10)分簇建立对应的概率模型，对概率矩阵B按式(11)采样生成新的子种群Pk；

② 从每类子种群中随机选择一个个体组成全局子种群I，并从I中随机选择父个体，通过差分变异算子式(7)生成新的子种群Q，并计算其目标函数值。

(5)环境选择：采用NSGA-Ⅱ非支配排序选择，从P∪Q∪PopX(t)中选择NX个优秀个体作为下一代种群PopX(t+1)。

(6)t=t+1，跳转到步骤(2)。

3 实验结果及分析

本文选择RM-MEDA[5]、基于差分进化采样(Differential Evolution Sampling，DES)的多目标分布估计算法DES-RM-MEDA[16]、基于规则模型的无聚类多目标分布估计算法FRM-MEDA[10]作为对比算法来测试AP-RM-MEDA算法的性能。由于本算法是基于RM-MEDA改进的，与之对比将突显所提算法的性能。与RM-MEDA采用高斯采样方法不同，DES-RM-MEDA将决策变量中的个体映射到隐空间中，然后采用差分变异算子进行变异操作，再映射回原空间中，由此避免对概率模型进行扩展。FRM-MEDA通过去聚类操作来消除聚类数目K值对算法的影响，同时引入全变量高斯模型来弥补去聚类操作对算法多样性的影响，从而保持了算法的良好性能。

3.1 多目标算法的评价指标

为了更直观、准确地体现以上4种算法的性能，本文选择世代距离(Generational Distance，GD)[17]和反世代距离(Inverted Generational Distance，IGD)[18]作为算法性能评价指标，具体如下：

① GD：该指标通过计算算法寻得的Pareto解集到真实Pareto前沿上的平均距离，定量地评价了算法的收敛性，其值越小说明算法求得的最优解集越逼近真实Pareto前沿。计算表达式为：

(12)

式中，d(x,p)表示个体xi到真实Pareto前沿的欧氏距离；|P*|表示算法寻得的Pareto解集中解的个数。

② IGD：该指标为综合性指标，通过计算真实Pareto前沿到算法得到的Pareto解集上的平均距离，其值越小越突出解的多样性和算法的收敛性。计算表达式为：

(13)

式中，|P|表示真实Pareto前沿中的参考点个数。

3.2 参数设置

在本文的实验中，算法的决策变量维度DX设为30，RM-MEDA，DES-RM-MEDA两种算法的聚类数目K值均设为5，而FRM-MEDA的K值为1。在RM-MEDA中，模型的缩放比例为0.25。DES-RM-MEDA和ADC-RM-MEDA中变异算子中的缩放因子F均设为0.4。

AP-RM-MEDA中，在执行混合算子产生新种群时，需要设置一个参数H来设置2种算子产生新个体的比例，由于差分变异算子利用了个体的信息，可以增加种群的多样性，但是在进化后期产生有效解的概率不大，所以引入迭代次数以控制该值，即：

H=0.2-0.1×iter/MaxIter，

(14)

式中，iter为当前迭代次数；MaxIter为最大迭代次数。

本文将以上4种算法利用文献[5]中的测试函数F1～F4，F7～F9和DTLZ2，共8个测试函数上进行实验比较。其中，F4，F8，DTLZ2属于三目标函数，F4中变量线性相关，F8中变量非线性相关，DTLZ2为变量无关测试函数，种群规模NX为200；F1，F2，F3，F7，F9为两目标函数；F1，F2，F3为变量线性相关测试函数；F7，F9为变量非线性相关函数，种群规模NX为200。对于两目标测试函数F1，F2，MaxIter设置为100，对于三目标测试函数，MaxIter设置为200，其余测试函数为1 000。对于每个测试函数，每种算法各单独运行20次。算法在各个测试函数所需的迭代次数、种群规模以及真实Pareto前沿的参考点个数如表1所示。

表1 各个测试函数所需的不同参数Tab.1 Different parameters required by each test function

3.3 重用策略的有效性

在AP-RM-MEDA中，为了降低AP聚类操作带来的计算开销，将重用连续L=20代都保持不变的聚类数目K值，而不再进行AP聚类。为了验证其有效性，使用带重用机制的和不带重用机制的AP-RM-MEDA算法分别对迭代次数1 000的测试函数F3，F7，F9进行实验验证。其中，不带重用机制是指算法每次迭代过程中都将进行AP聚类操作，得到聚类数目K。在独立运行算法20次之后，2种算法得到的评价指标的均值、方差以及带重用机制算法的平均聚类次数如表2所示。

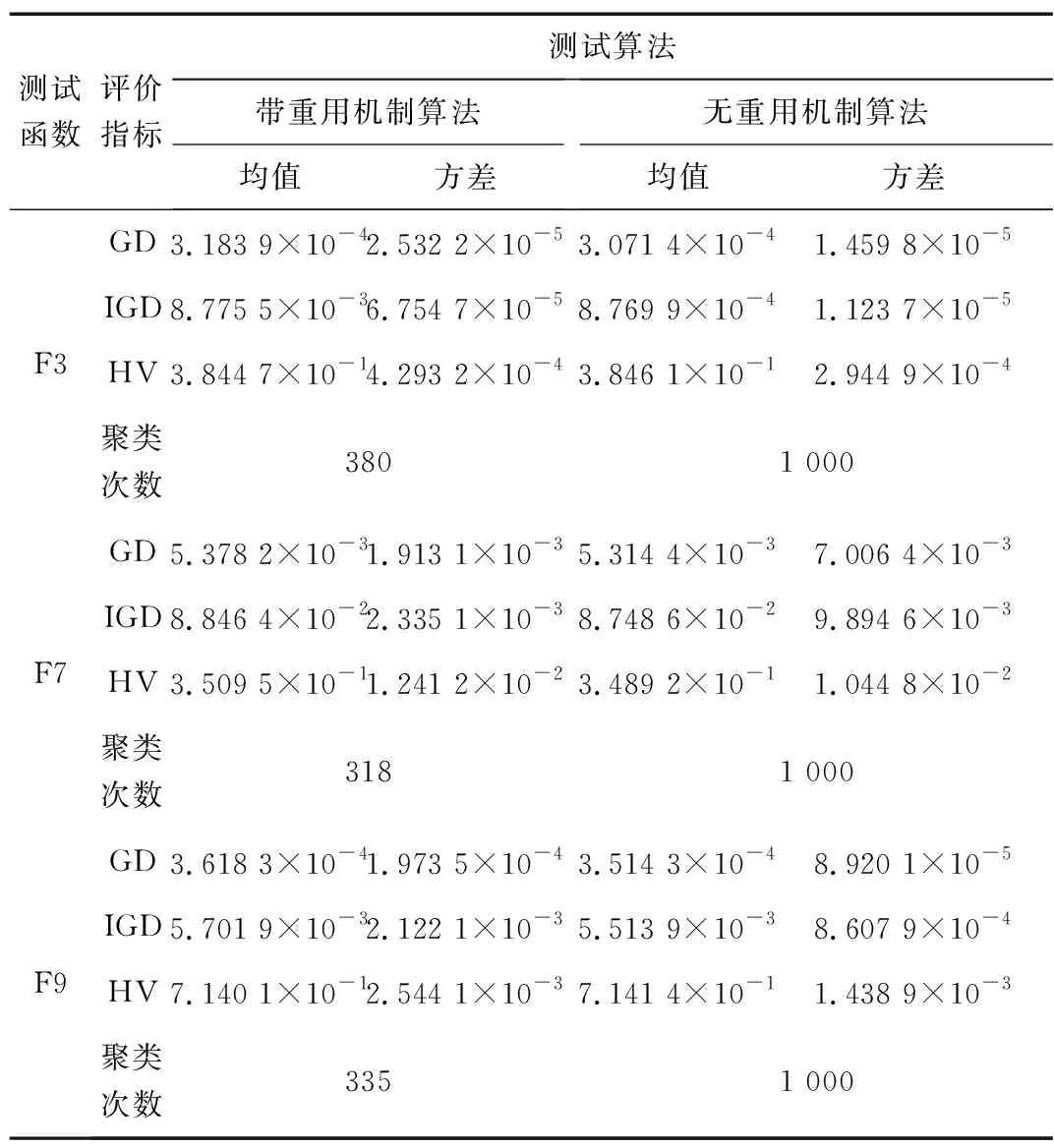
表2 2种算法在测试函数上的GD，IGD和HV的均值及方差Tab.2 The mean and variance of GD, IGD and HV of two algorithms on the test function

表2的数据结果显示，对于有或无重用机制的2种算法在以上测试函数上所表现的性能并没有较大差异。从聚类次数上看，带有重用机制的算法需要的聚类次数大大减少，而没有重用机制的算法均需要聚类1 000次。基于上述实验结果可以证明，在对提出的AP-RM-MEDA算法性能影响不大的前提下，重用机制能有效地降低算法的计算开销。

3.4 实验对比结果及分析

表3、表4和图1分别是4种算法在两目标测试函数上测试得到的评价指标GD和IGD的均值、方差及解集构成的Pareto前沿。表3和表4中，为了更好地突出最好的数据值，对结果数据中最好的值进行加粗表示。

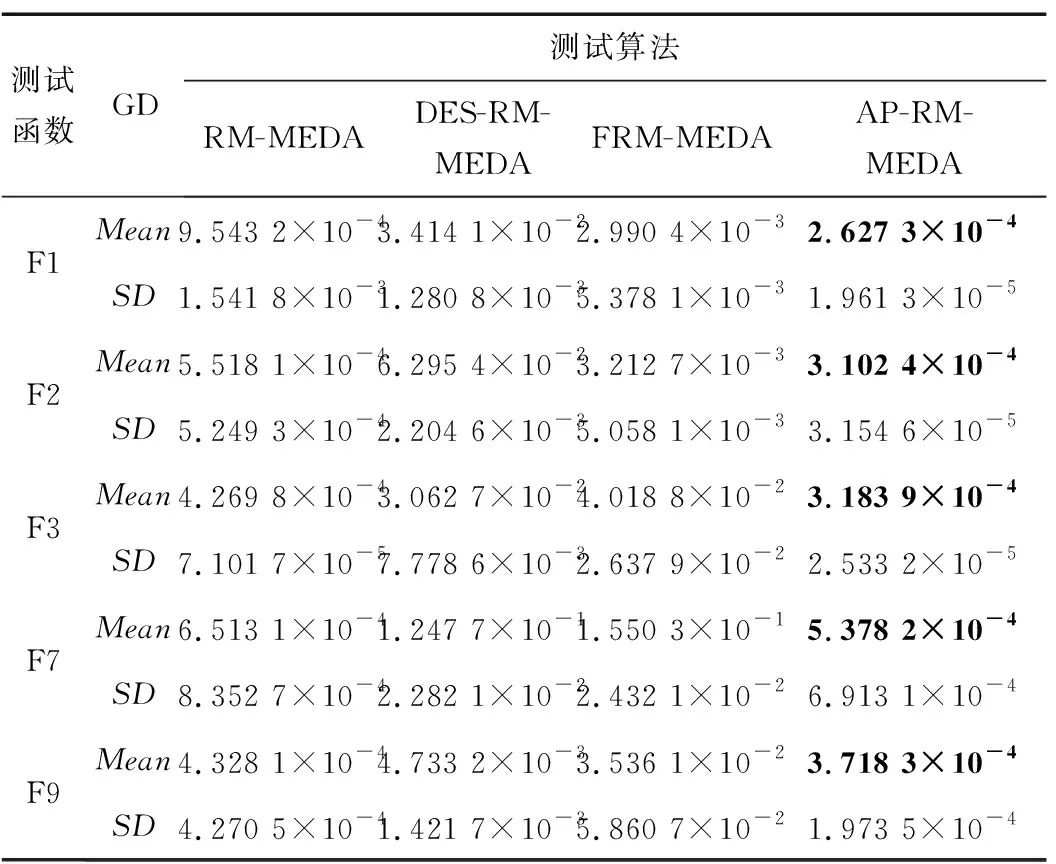
表3 4种算法在两目标测试函数上的GD的均值及方差Tab.3 The mean and variance of GD of four algorithms on the two-objective test functions

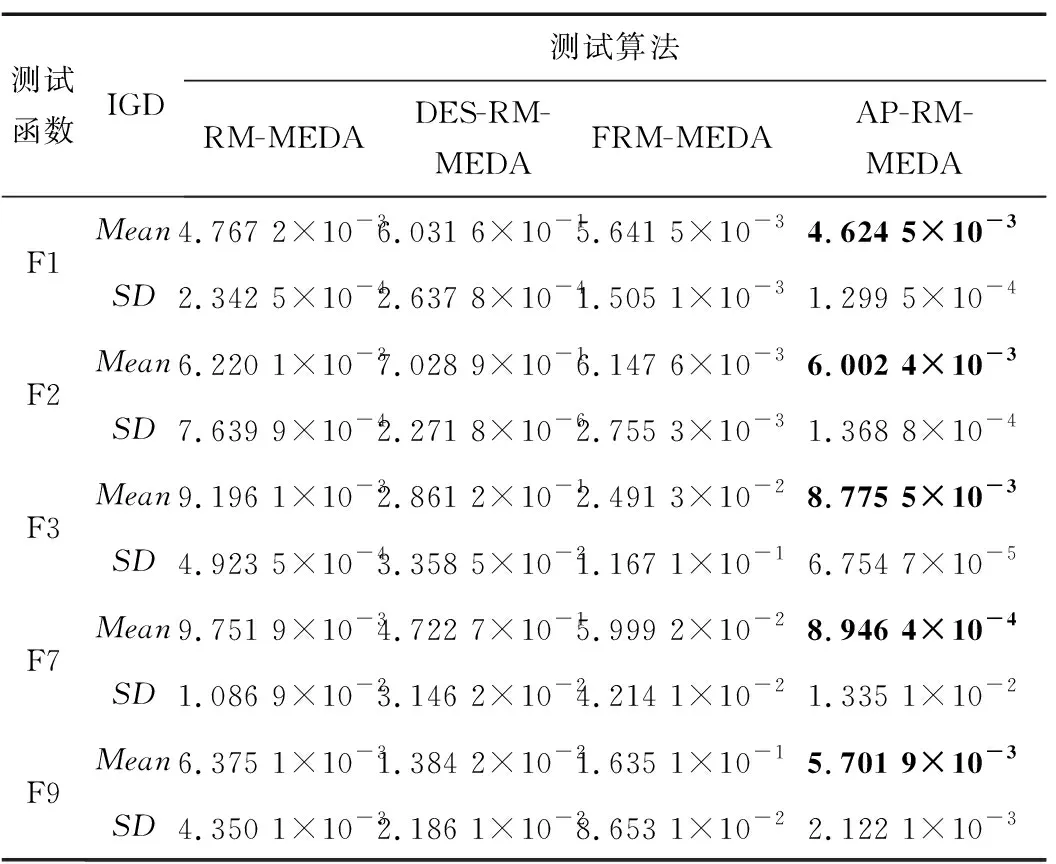
表4 4种算法在两目标测试函数上的IGD的均值及方差Tab.4 The mean and variance of IGD of the four algorithms on the two-objective test functions

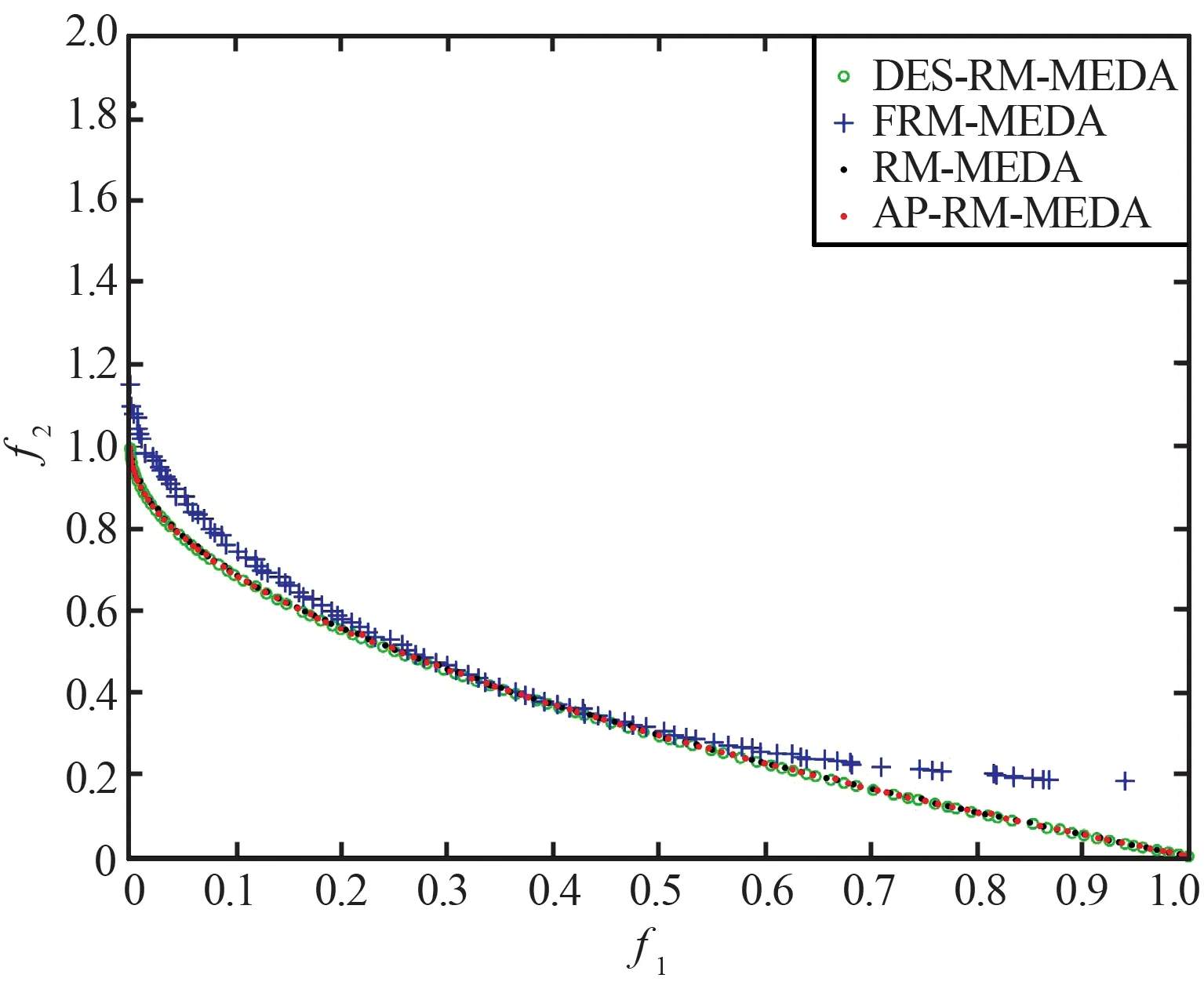
(a) 4种算法在F1函数上获得的PF对比图

(b) 4种算法在F2函数上获得的PF对比图

(c) 4种算法在F3函数上获得的PF对比图

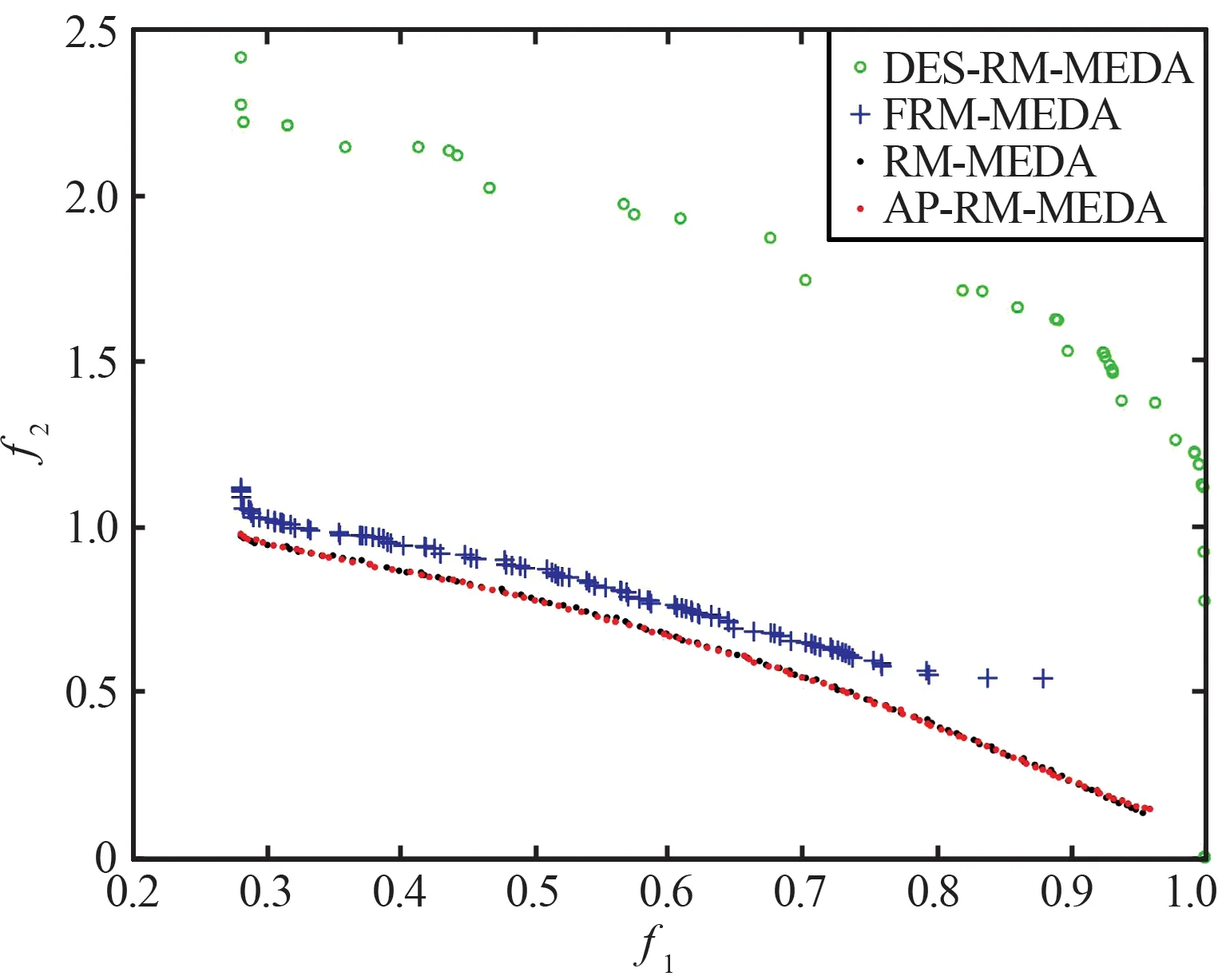
(d) 4种算法在F7函数上获得的PF对比图

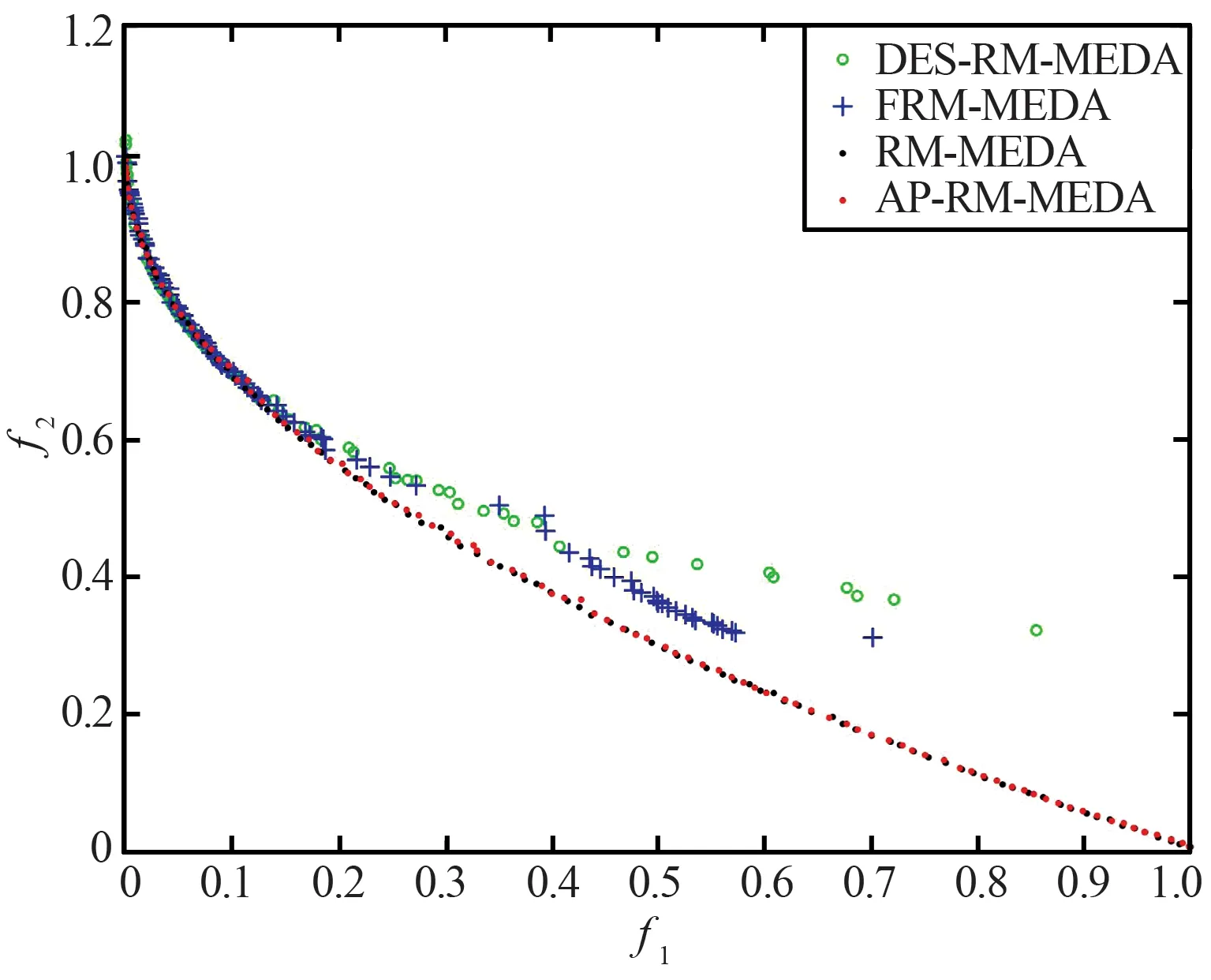
(e) 4种算法在F9函数上获得的PF对比图图1 4种算法在两目标函数上获得的Pareto前沿对比Fig.1 Comparison of Pareto front obtained by four algorithms on two-objective functions

从表3和表4中的数据可以看出，在绝大多数两目标测试函数上，AP-RM-MEDA算法与对比算法相比具有更好的表现。从表3中GD的结果数据可看出，对于较为简单的测试函数，无论是凸函数还是凹函数(如F1和F2)，AP-RM-MEDA算法的表现更加稳定，收敛能力得到明显提升。对于较困难的测试函数(如F3，F7和F9)，AP-RM-MEDA算法的收敛效果也好于其他对比算法。表4中IGD的数据显示，在收敛性和多样性方面，AP-RM-MEDA算法的综合性能表现也不差于RM-MEDA。

表5和表6分别是4种算法在三目标测试函数上测试得到的评价指标GD和IGD的均值、方差。在表5和表6中，为了更好地突出最好的数据值，对结果数据中最好的值进行加粗表示。

表5 4种算法在三目标测试函数上的GD的均值及方差Tab.5 The mean and variance of GD of four algorithms on the three-objective test functions

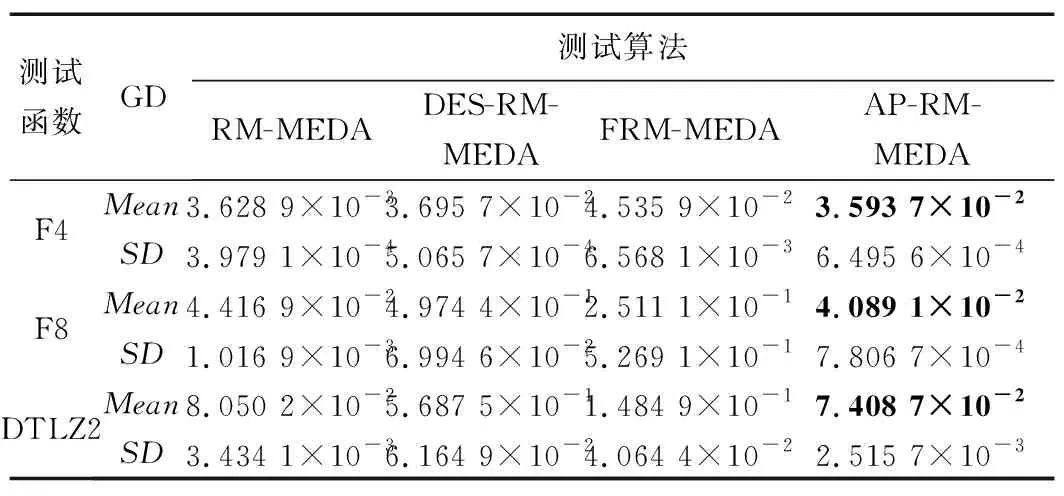
表6 4种算法在三目标测试函数上的IGD的均值及方差Tab.6 The mean and variance of IGD of four algorithms on the three-objective test functions

4种算法在三目标测试函数F4上获得的Pareto前沿对比如图2所示。

(a) RM-MEDA获得的PF与真实PF对比图

(b) DES-RM-MEDA获得的PF与真实PF对比图

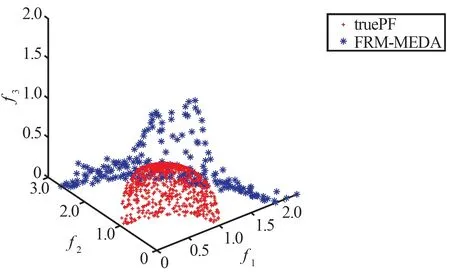
(c) FRM-MEDA获得的PF与真实PF对比图

(d) AP-RM-MEDA获得的PF与真实PF对比图图2 4种算法在F4上获得的Pareto前沿Fig.2 Pareto front obtained by four algorithms on F4

4种算法在三目标测试函数F8上获得的Pareto前沿对比如图3所示。

(a) RM-MEDA获得的PF与真实PF对比图

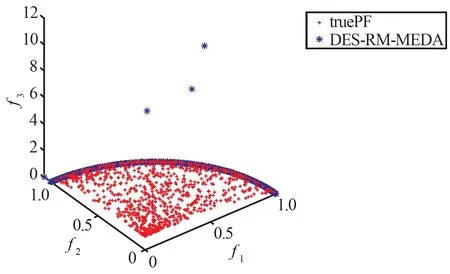
(b) DES-RM-MEDA获得的PF与真实PF对比图

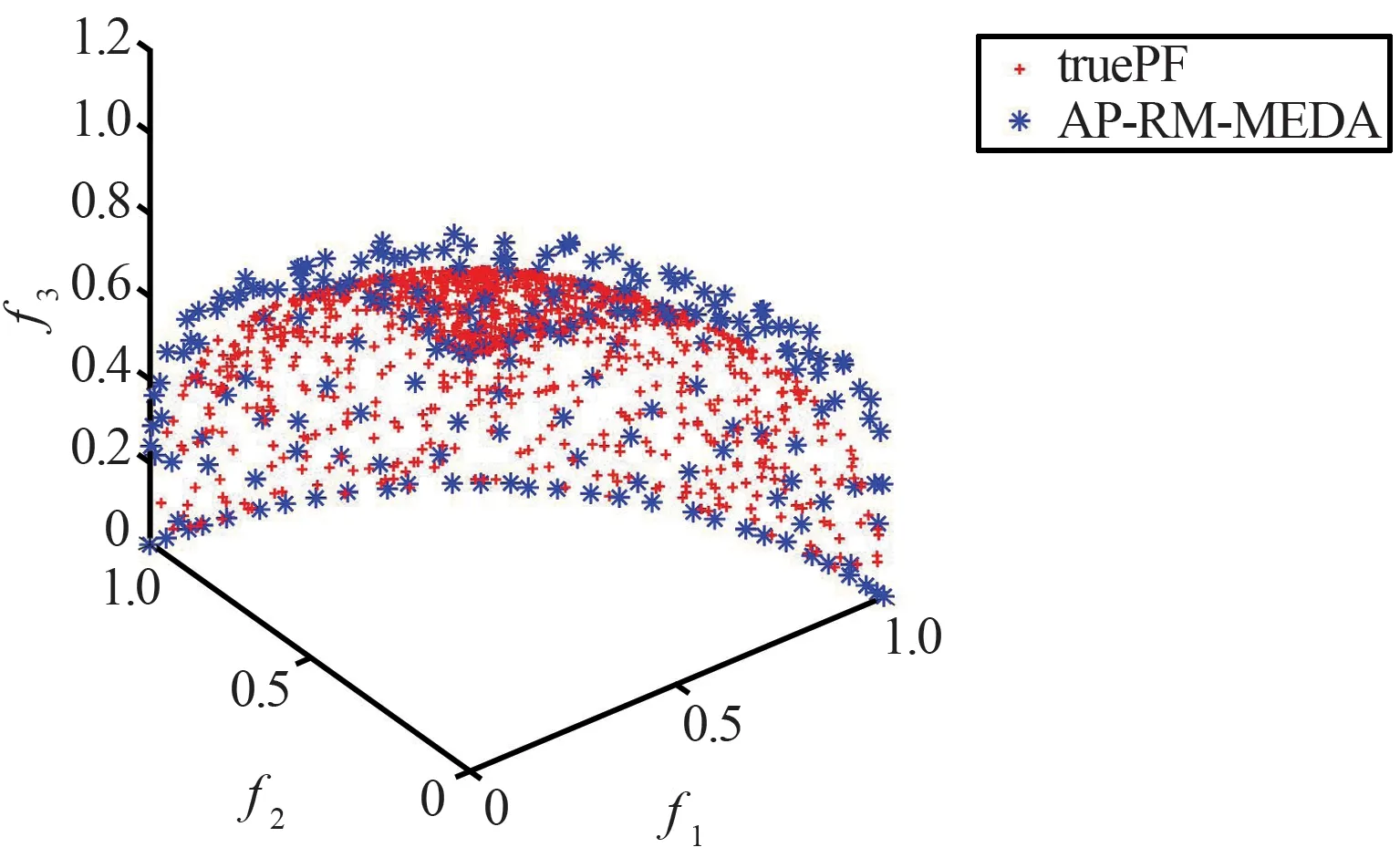
(d) AP-RM-MEDA获得的PF与真实PF对比图图3 4种算法在F8上获得的Pareto前沿Fig.3 Pareto front obtained by four algorithms on F8

4种算法在三目标测试函数DTLZ2上获得的Pareto前沿对比如图4所示。

(a) RM-MEDA获得的PF与真实PF对比图

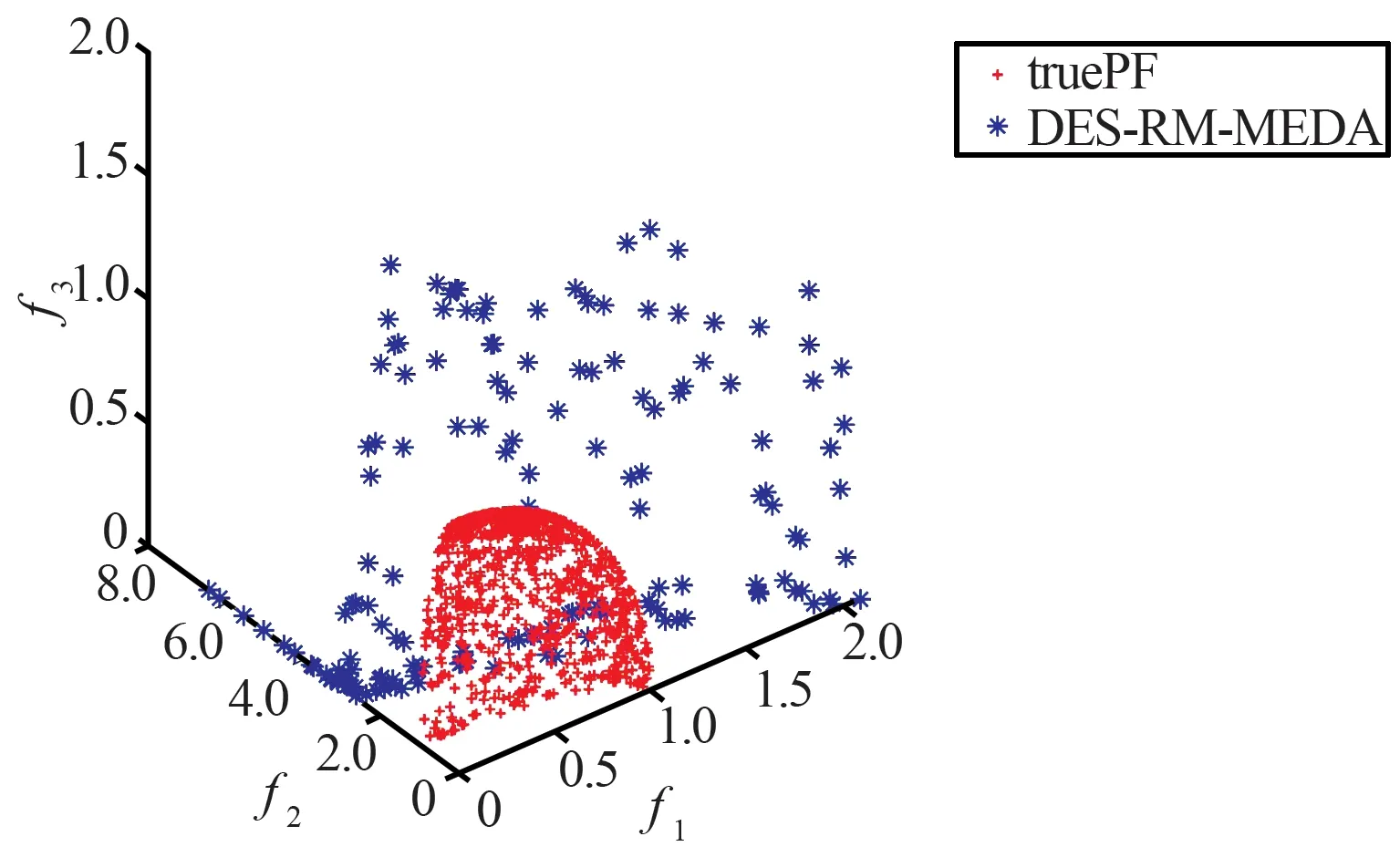
(b) DES-RM-MEDA获得的PF与真实PF对比图

(c) FRM-MEDA获得的PF与真实PF对比图

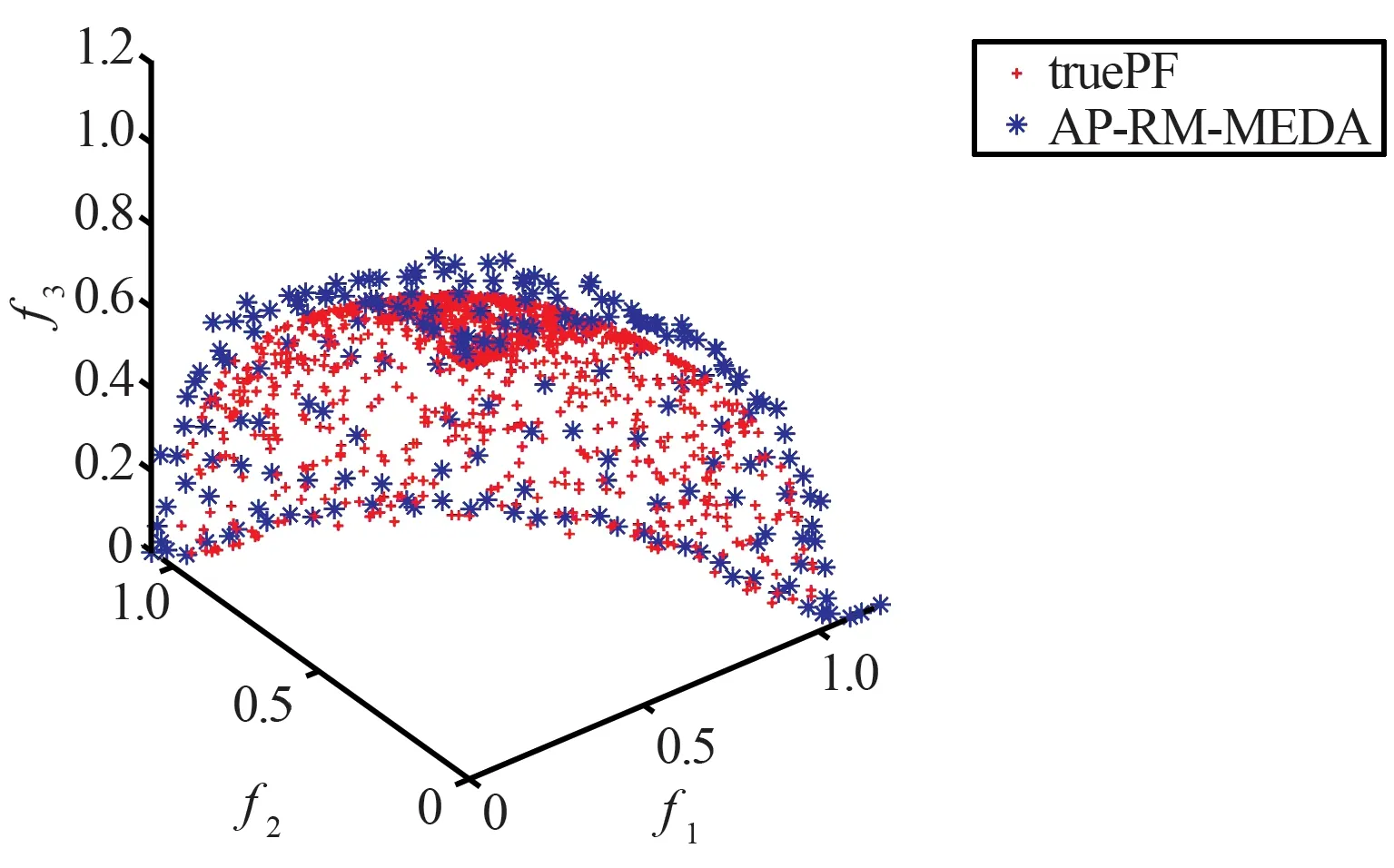
(d) AP-RM-MEDA获得的PF与真实PF对比图图4 4种算法在DTLZ2上获得的Pareto前沿Fig.4 Pareto front obtained by four algorithms on DTLZ2

从表5、表6和图2～图4中的数据可以看出，在三目标测试函数上，AP-RM-MEDA算法与对比算法相比，其非支配解都可以更好地收敛到真实Pareto前沿上，其综合性能也有一定程度的提升。

结合上述表中的对比数据和Pareto前沿的对比图表明，AP-RM-MEDA算法在收敛性和多样性方面有着较优的表现。

4 结束语

本文提出的基于AP的多目标分布估计算法中，通过引入AP聚类操作来自动确定种群需要聚类的数目，避免了人为确定聚类数目的不准确性以及聚类数目与实际所需不等时以致算法无法建立正确的概率模型。同时，为了减小AP聚类操作所带来的额外计算开销，设计了一种将聚类数目进行重用的策略，并通过实验验证了其有效性。通过混合算子共同生成新的个体，结合种群的整体和个体信息，提高了算法的全局搜索能力。与其他3种算法的对比实验结果表明，本文提出的AP-RM-MEDA算法与其他几种性能较好的算法相比，收敛性和整体性能均有提升，同时在绝大多数两目标和三目标测试问题中，都有着更好的表现。