COVID-19影响下的城市PM2.5浓度预测
2023-02-18孟春阳谢劭峰魏朋志张亚博唐友兵
孟春阳,谢劭峰,魏朋志,张亚博,唐友兵,熊 思
(1.桂林理工大学 测绘地理信息学院,广西 桂林 541006; 2.湖北科技学院 资源环境科学与工程学院,湖北 咸宁 437100)
0 引言
PM2.5是指大气中空气动力学当量直径小于或等于2.5 μm的颗粒物,是空气污染的主要来源,可以直接进入肺泡,危害人类安全。
近年来,国内外众多学者利用多种方法对PM2.5浓度进行预测研究。文献[1]利用快速傅里叶变换(Fast Fourier Transform,FFT)与长短时记忆(Long Short-Term Memory,LSTM)网络结合的方法,建立PM2.5浓度预测模型,对PM2.5浓度进行预测。文献[2]通过获取的观测数据,采用主成分分析法处理,构建鹰潭市PM2.5浓度预测模型。文献[3]对于存在缺陷的多元线性回归和时间序列模型进行优化,提出了基于多元时间序列的PM2.5浓度预测的方案。文献[4]对预测因子利用遗传算法进行优化后的神经网络建立PM2.5浓度的预测模型,并对模型预测结果进行可行性分析。文献[5]通过数据分析广西主要城市PM2.5浓度和大气可降水量(Precipitable Water Vapor,PWV)的变化,构建多元线性回归-差分自回归移动平均(MLR-ARIMA)模型,对3市PM2.5浓度变化进行短期预测。文献[6]采用反距离加权插值获得的PWV和风速值,建立3种模型对中南地区4省1区2年春节期间进行PM2.5浓度估算。文献[7]研究PM2.5浓度的空间覆盖格局,利用中国中南地区的340个PM2.5浓度数据,建立6个插值模型,分析不同时段PM2.5浓度的变化规律。文献[8]利用国际GNSS服务(International GNSS Service,IGS)提供的天顶对流层延迟产品,研究其与雾霾之间的相关性。文献[9]等运用贝叶斯时空模型对京津冀区域的PM2.5浓度变化建立预测模型。文献[10]通过对各个季节PM2.5浓度预测,利用主成分分析法(Principal Component Analysis,PCA)进行数据降维,分析各个季节以及气象因素对PM2.5浓度的影响。文献[11]采用2013—2016年PM2.5与臭氧数据分析其相关性,发现PM2.5与臭氧之间存在明显的季节变化,且PM2.5浓度逐年有降低趋势,而臭氧越来越难以控制。文献[12]选取北京有雾霾和无雾霾2个时间期,分别在2个时期分析AQIZTD和反演得到的PWV之间的相关性,研究结果表明在3个时期的大部分时间内三者均相关性显著。文献[13]采用了基于深度神经网络(Deep Neural Network,DNN)的反演模型,对PM2.5浓度进行反演,并将反演得到的进行验证,结果表明反演得到的PM2.5浓度精度高、相关性强,能够分析其时空演变特征及季节变化特征。文献[14]通过北京市2019—2021年空气质量指数(AQI)以及6大污染物浓度变化,采用ARIMA模型和神经网络分析AQI与污染物之间的相关性,研究结果表明PM2.5,PM10和O3对AQI影响最大且有明显的季节性趋势。
上述研究主要结合大气污染物、气象因素等方面与PM2.5进行相关性分析,对PM2.5浓度进行预测,且均取得了较好的预测结果,但缺少对2020年爆发至今的新冠肺炎疫情期间的城市PM2.5浓度变化规律及预测模型适用性研究。2020年初,新冠肺炎疫情爆发,全国人口流动、车辆出行以及工业生产等大幅度降低,PM2.5浓度相比2019年整体有下降[15],因此疫情期间的城市PM2.5浓度变化情况有一定的研究价值。本文通过ARIMA,BP神经网络和PSO-BP三种模型比较在2019年与2020年疫情期间预测PM2.5浓度的适用性,为疫情期间的PM2.5浓度预测与防治工作提供一定的理论基础与改进思路。
1 数学模型
1.1 ARIMA模型
ARIMA模型全称为自回归积分滑动平均(Auto regressive Integrated Moving Average,ARIMA)模型,其中ARIMA(p,d,q)称为差分自回归移动平均模型,AR是自回归,p为自回归项,MA为移动平均,q为移动平均项数,d为时间序列成为平稳时所做的差分次数,该模型可表示为[16]:
(1)
式中,L为滞后算子;Φ(L)为L的SAR多项式;Δd=(1-L)d,d为差分阶数;c为差分;Θ(L)为L的SMA多项式;E为期望;Var为方差;εt和εs为误差;yt为单变量时间序列。
1.2 BP神经网络模型
BP(Back Propagation)神经网络是根据误差逆传播算法训练的多层前馈网络中的一种,它由信息的前向传播和误差的反传播组成,是应用面最广的神经网络模型之一。通过外部输入信息被输入层上的每个神经元接收,之后由它们传递给中间层的神经元,中间层可以根据信息转换的能力设计为单隐藏层或多隐藏层,将信息进一步处理,再通过最后一个隐藏层传递到输出层上的每个神经元。信息的处理结果由输出层导出到外部,当实际输出和预期输出相互矛盾时,就会进行误差的反传播。通过输出层,每个权重根据误差的梯度下降进行修订,并逐层反向传播到隐藏层和输入层,BP神经网络模型的基本公式为[17]:
(2)
式中,W为权重;n为层数;η为学习率;E为误差函数的梯度 ;αΔW(n-1)为全权重增量。
1.3 PSO-BP模型
(Particle Swarm Optimization)PSO算法是由Kennedy和Eberhart通过对于鸟类摄食行为的研究所提出的一种群体智能优化算法。在算法中,每个粒子代表问题的潜在解决方案,并具有由适应度函数确定的适应度值,其速度决定粒子运动的方向和距离,并根据自己和其他粒子的运动经验动态调整,从而实现解决方案空间中的个体化优化。由于PSO算法较强的全局优化能力,能够大大提高神经网络的泛化能力,通过PSO优化BP神经网络的过程中,神经网络的权重和阈值映射到PSO算法的粒子,将最优个体的权值和阈值分配给BP神经网络,实现网络训练。PSO的适应度函数是神经网络的输出误差,其公式为[18-19]:
(3)
式中,ni为训练集的样本个数;Oiq,Tiq分别是训练样本q在第i粒子的位置所确定的权值和阈值的输出。
1.4 方法流程
针对BP神经网络、ARIMA等传统模型预测精度不高等缺点,通过采用粒子群算法对BP神经网络模型进行优化,通过粒子适应度确定个体最优和群体最优位置,设定模型粒子数量为10,迭代次数为30,当误差达到预期目标后,模型根据最优权阈值得到最佳预测结果,3种模型算法具体流程如图1所示。

图1 模型流程Fig.1 Model of the process
2 实验数据与分析
2.1 数据来源
在2020年1月—3月新冠疫情期间,上海、长春、武汉和北京4市累计出现新冠患者51 147人。4市在疫情爆发后均采取严格的进出城市及人员外出的限制政策,武汉市采用封城来减少疫情期间人群流动和车辆出行等,对PM2.5浓度变化有一定影响。针对不同城市的疫情情况,根据城市间人口流动及人口密度不同的情形下,研究模型在2019年非疫情期间与2020年疫情期间的PM2.5浓度预测对比,及其在2个时期的整体适用性。
本文建模分别选取4个城市2019年与2020年的1月—3月的小时数据。其中大气污染物数据为SO2,NO2,CO,O3,PM10以及PM2.5小时数据资料,来源于天气后报(http://www.tianqihoubao.com/aqi/);气象资料采用气温、气压、湿度和风速4要素的小时观测数据,来源于中国气象数据网(http://data.cma.cn);通过IGS提供的小时ZTD的数据,来源于美国国家航空和航天局(https://cddis.nasa.gov/archive/gnss/products/troposphere)。
2.2 相关性分析
建模之前需要对影响PM2.5浓度的因素进行相关性分析,以确保对变量的适用性。本文采用非参数分析法分别对2019年与2020年的1月—3月上海、长春、武汉和北京4个城市的PM2.5影响因子进行相关性分析,结果如表1和表2所示。

表1 4城市PM2.5浓度与空气污染物相关性Tab.1 Correlation between PM2.5 concentration and air pollutants in 4 cities
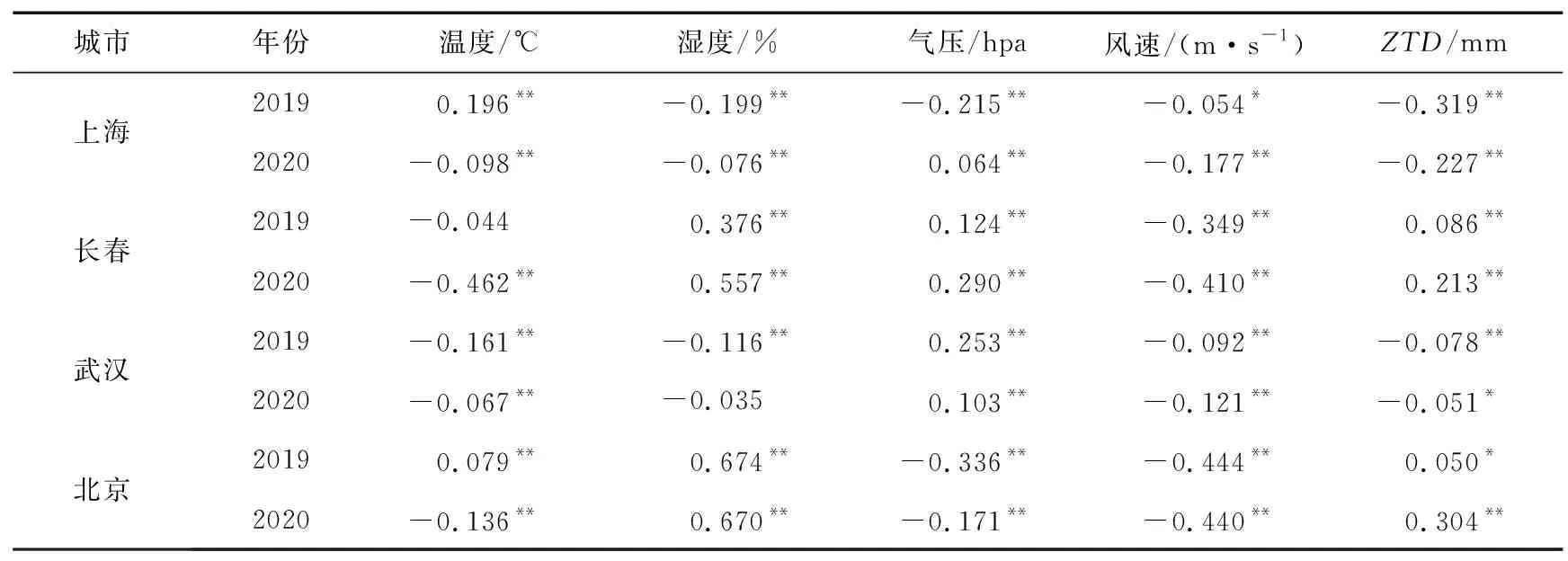
表2 4城市PM2.5浓度与气象因素和ZTD相关性Tab.2 Correlation between PM2.5 concentration and meteorological factors and ZTD in 4 cities
由表1可知,PM2.5与PM10,SO2,NO2,CO均为正相关,与O3呈负相关性,其中4个城市在2019年与2020年1月—3月中,PM2.5与PM10,SO2,NO2,CO,O3之间存在强相关性。从表2可以看出,风速对PM2.5影响最大,均呈现负相关性,在整体的气象因素中相关性最强,温度、湿度和气压次之。对于PM2.5与ZTD的相关性分析中,长春与北京2市呈正相关,上海与武汉2市呈负相关。由整体相关性可知,4个城市的PM2.5与各因素之间相关性显著,可以用于建模分析。
2.3 四市PM2.5变化规律分析
为分别探究上海、长春、武汉和北京4个城市在2019年与2020两年中1月—3月的小时PM2.5浓度变化规律及特征,现将4个城市1月—3月的PM2.5小时数据变化情况组成一个连续时间序列进行分析,为保证时间对比一致性,将2020年2月29日数据舍去,其变化趋势如图2所示。
根据图2中4个城市在2019年和2020年1月—3月的小时PM2.5浓度值变化情况可以看出,上海与武汉2市在2020年1月—3月的PM2.5浓度值基本低于2019年;北京市PM2.5浓度在2020年1月底与2月上旬有短暂波动高于2019年变化,整体变化趋势中大部分时间弱于2019年;长春市在2020年1月中,PM2.5浓度基本高于2019年,在2月和3月低于2019年,其中在2020年1月份中PM2.5小时最高浓度高达400 μg/m3,其原因可能为春季降雨较少,加之疫情期间居家人口增加、城市供暖需求增大,导致浓度飞速上升。
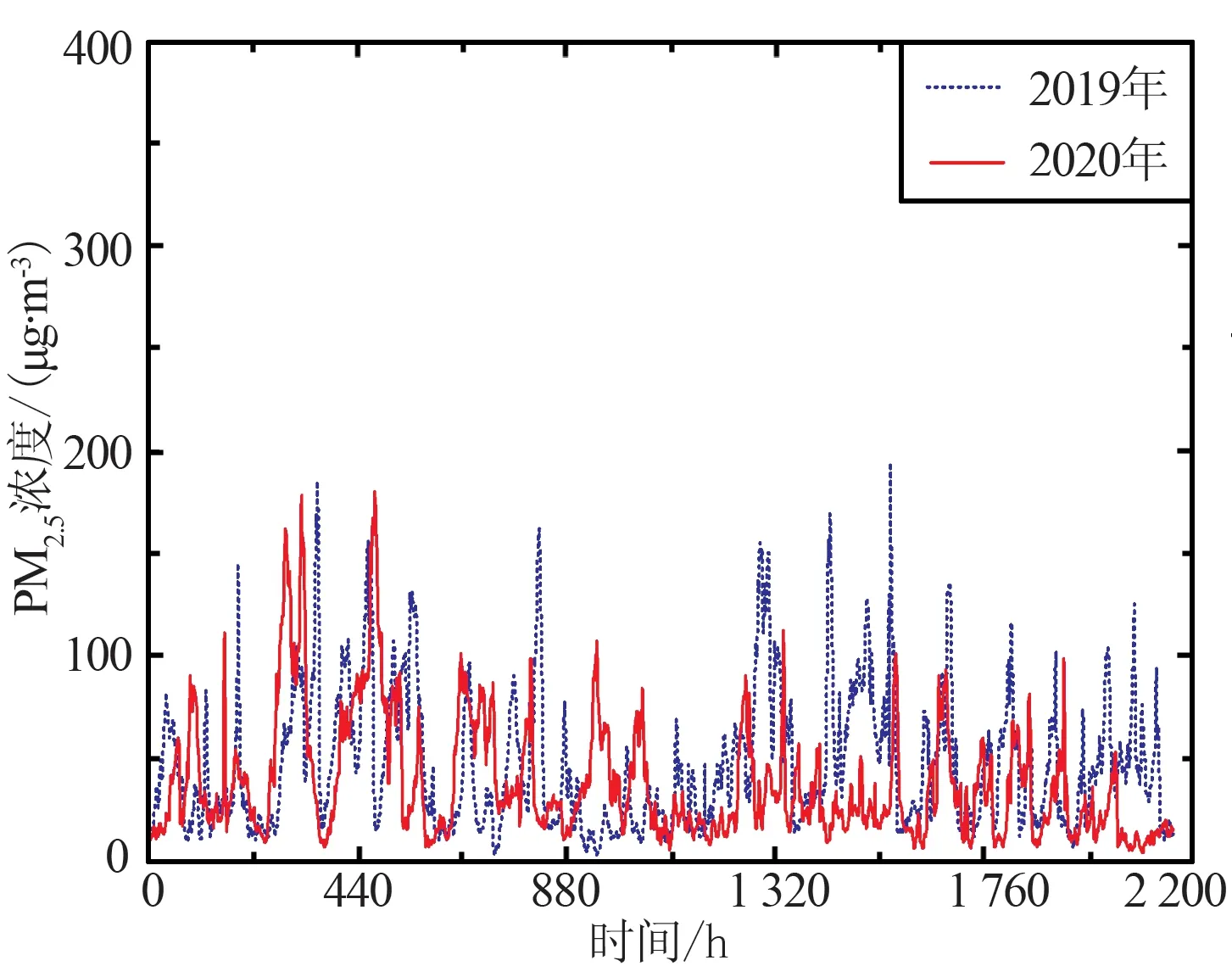
(a) 上海PM2.5浓度变化
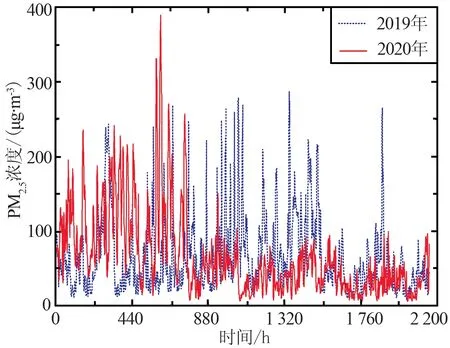
(b) 长春PM2.5浓度变化
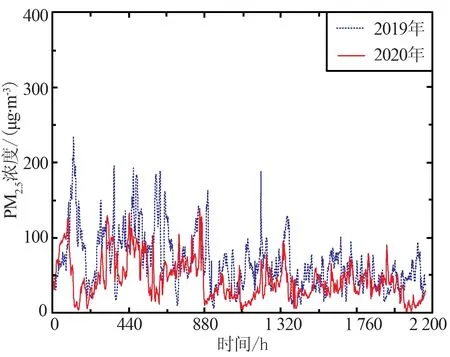
(c) 武汉PM2.5浓度变化

(d) 北京PM2.5浓度变化图2 四市PM2.5小时浓度值变化Fig.2 Hourly change of PM2.5 concentration in four cities
从整体上看,4个城市在2020年1月—3月的PM2.5浓度基本要低于2019年。在2020年1月—3月疫情期间,武汉市作为疫情的重灾区,在1月封城后,PM2.5浓度出现显著下降趋势,空气质量相比较2019年有极大的改善;上海市在此期间人群流动及外出的减少,导致浓度基本低于2019年;北京和长春2市由于疫情的影响,在1月—3月供暖期间供暖需求大幅增加,出现短暂PM2.5浓度大幅波动。在疫情的影响,人群流动性、工厂生产和日常出行量等的减少,空气质量有效改善,但对于重工业及供暖城市,疫情期间PM2.5依旧远超标准值,因此由于疫情影响的PM2.5浓度降低并没有解决污染源头问题,因此PM2.5的防治工作依旧要继续。本文分别选取4市2019年与2020年1月1日—3月29日的数据作为模型训练集,预测未来2个时期的48 h PM2.5浓度变化,并与3月30日和31日数据进行对比。选取3种模型分别对于城市疫情期与非疫情期2个时期的预测研究是富有意义的,对比2个时期的PM2.5浓度变化规律及预测精度,对未来时间内在疫情影响下的城市PM2.5浓度预测有着至关重要的作用。
3 实验结果分析与讨论
3.1 模型评价标准
为了更加直观对比模型对于数据的适用性,本文采用均方根误差(Root Mean Square Error,RMSE)、平均绝对误差(Mean Absolute Error,MAE)以及平均绝对百分比误差(Mean Absolute Percentage Error,MAPE)对模型估算的结果的进行精度评估:
(4)

3.2 预测结果与分析
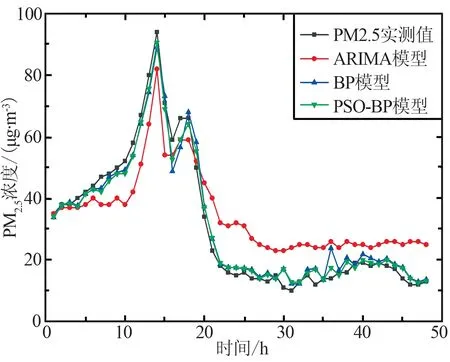
为了验证ARIMA,BP神经网络和PSO-BP三种模型在疫情期与非疫情期的预测能力,分别选取2019年与2020年1月1日—3月29日的PM2.5浓度、大气污染物、气象因素以及ZTD的小时数据进行建模,预测4市2个时期未来48 h的PM2.5浓度数据,并与3月30日和31日实测值对比。其中上海、长春、武汉和北京4市在每个时期1月1日—3月29日的PM2.5浓度训练样本有效数据的个数分别为2 109,2 106,2 112和2 102,大气污染物、气象要素及ZTD为影响因素,PM2.5浓度预测样本个数为48,各模型预测结果如图3和图4所示,其中(a)和(c)为4市2019年预测结果,(b)和(d)为4市2020年预测结果。
(a) 上海(2019年)

(b) 上海(2020年)
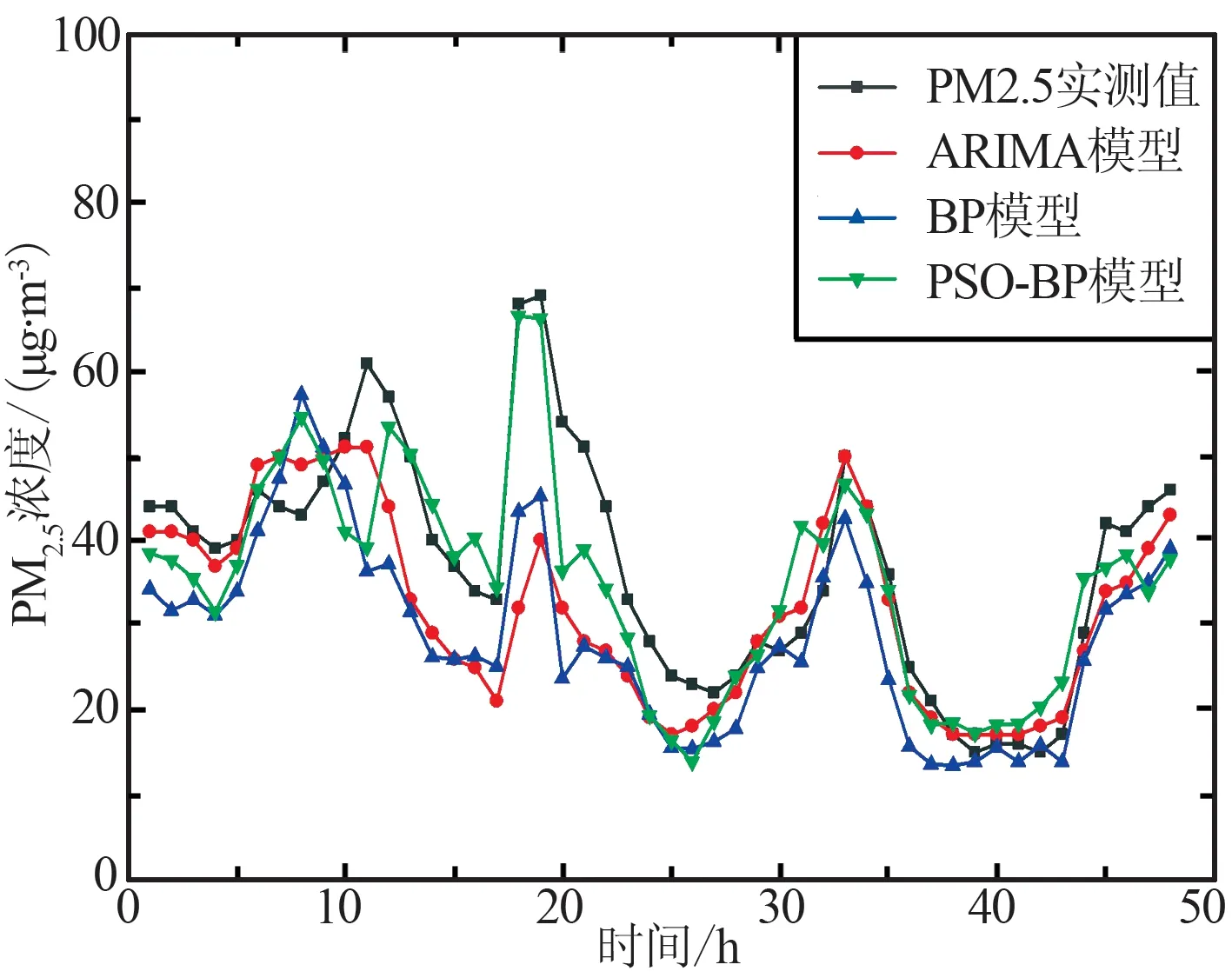
(c) 长春(2019年)
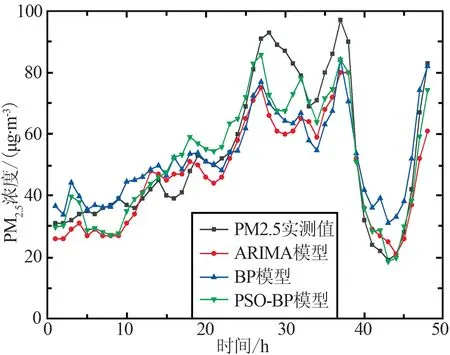
(d) 长春(2020年)图3 上海市、长春市预测结果对比Fig.3 Comparison of forecast results in Shanghai and Changchun
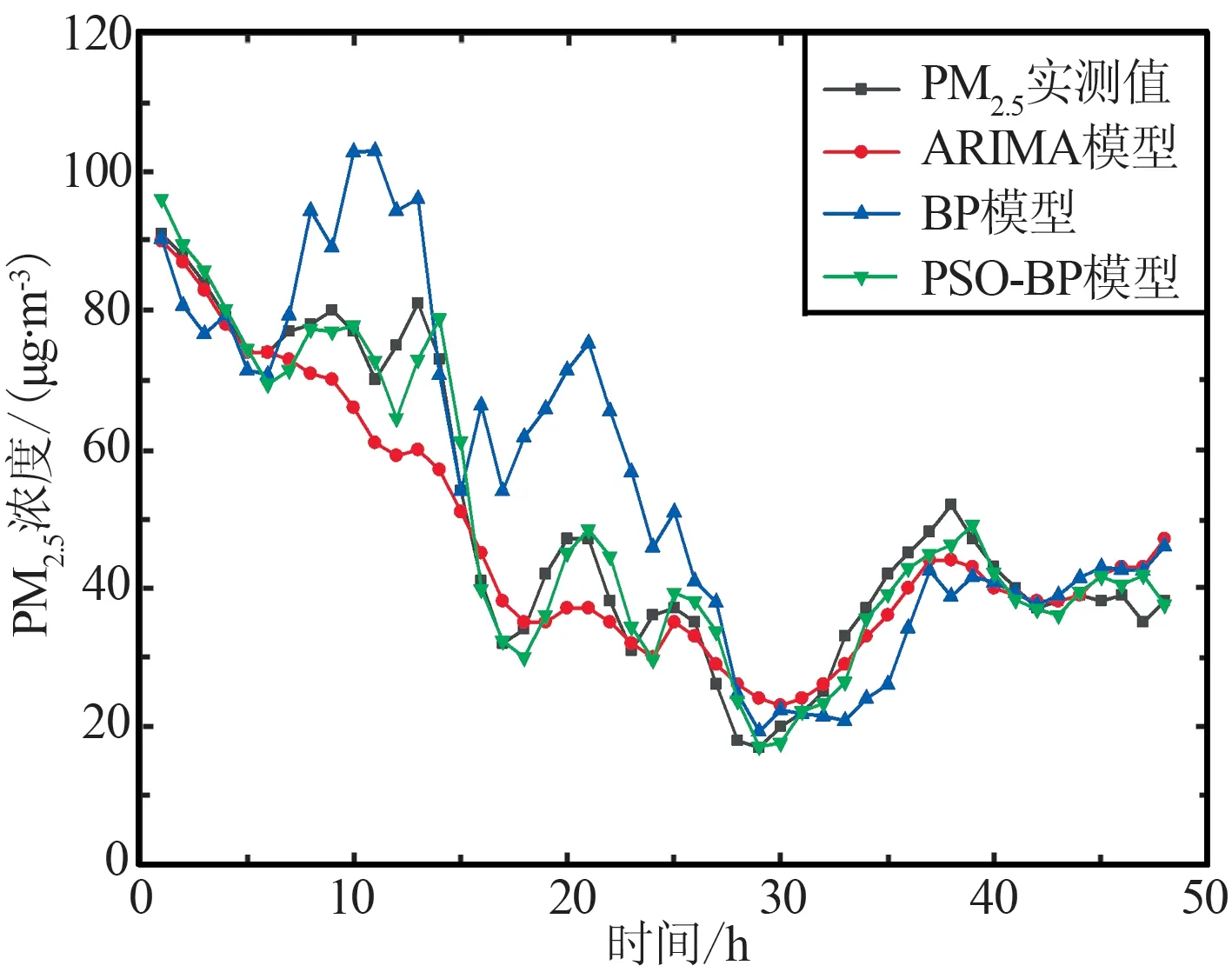
(a) 武汉(2019年)
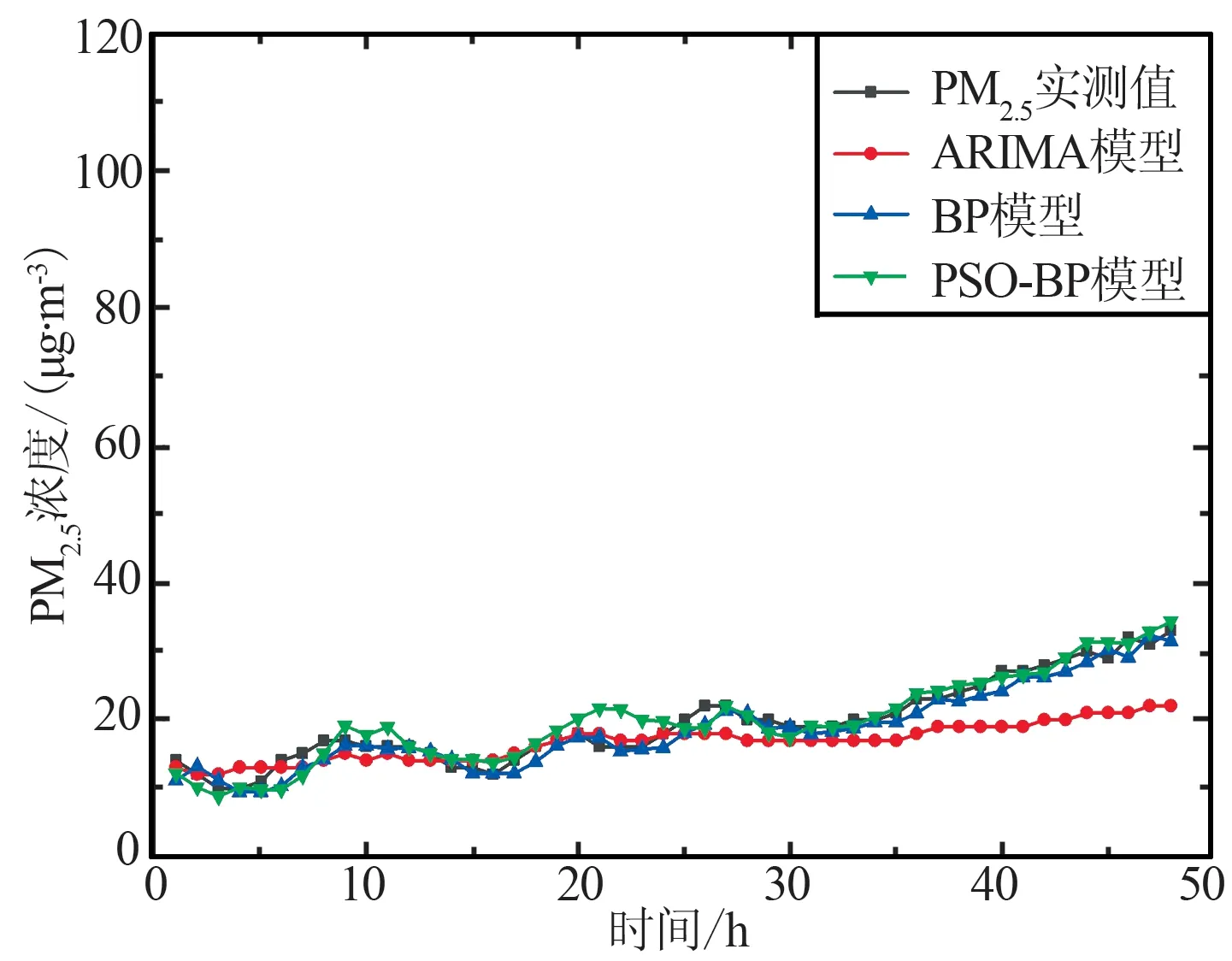
(b) 武汉(2020年)

(c) 北京(2019年)

(d) 北京(2020年)图4 武汉市、北京市预测结果对比Fig.4 Comparison of forecast results in Wuhan and Beijing
由图3和图4可以看出,各模型总体变化趋势相同,4个城市在非疫情期和疫情期的预测适用性均良好,可以基本模拟出预测未来48 h的整体PM2.5浓度变化趋势。从非疫情期和疫情期2个时期中的PM2.5真实值曲线对比可以看出,由于新冠肺炎疫情的影响,上海与武汉2市相较往年人群出行、中转及各类交通量均出现减少,并且武汉市在疫情期采取了严格的封城措施,导致2市疫情期PM2.5浓度远低于非疫情期;在1月—3月期间北京与长春处于供暖时期,其中北京市由于疫情期间供暖时间由每年3月15日24时停止延长至3月31日24时,加之人流减少,居家人口增加,供暖及用电高于往年,2市的PM2.5浓度疫情期高于非疫情期。由3个模型对于4市PM2.5浓度预测曲线与实测PM2.5浓度曲线对比可以看出,ARIMA模型在2019年上海市、2020年武汉市和BP神经网络模型在2019年武汉市、2020年上海与北京2市的预测结果与实测值有偏差,其余时期预测结果均较好。PSO-BP模型在2个时期中预测曲线趋势基本贴合实测曲线趋势,预测效果均较好,在3个模型中PSO-BP在2个时期中预测曲线与实测曲线均最为贴近,预测准确性高,说明PSO-BP模型相较于另外2个模型具有更好的模型适用性。
为了更加准确地对比各模型预测结果的精度及模型适用性,采用RMSE,MAE,MAPE三种评价指标进行评定,结果如表3所示。

表3 四市模型预测精度Tab.3 Forecast accuracy of the four-city model
由表3中各个模型预测3月30日和31日的PM2.5浓度的预测精度可以看出,ARIMA模型在2019年长春、武汉、北京3市和2020年上海、长春、北京3市的RMSE,MAE,MAPE的值均低于BP神经网络模型,BP神经网络模型在2019年上海市和2020年武汉市的RMSE,MAE,MAPE的值低于ARIMA值,PSO-BP模型在2019和2020年的预测精度均优于ARIMA模型和BP神经网络模型。
由图3、图4和表3可知,上海、武汉2市在非疫情期PM2.5浓度基本为10~110 μg/m3,而在疫情期PM2.5浓度为0~40 μg/m3,说明由于疫情管控使得2个城市在此期间空气质量得到改善,对比3个模型预测精度可知,PSO-BP模型相比ARIMA模型和BP模型,在上海和武汉2市非疫情期RMSE分别提升73.5%,22.6%和39.4%,71.2%,MAE提升了76.8%,17.8%和36.0%,69.9%;疫情时期RMSE分别提升49.0%,82.9%和70.2%,12.4%,MAE提升了48.5%,82.7%和67.0%,13.2%。长春、北京2市在非疫情期PM2.5浓度为0~80μg/m3,在疫情期PM2.5浓度为10~100 μg/m3。由图3、图4曲线对比可以看出,疫情期PM2.5浓度基本高于非疫情期,考虑到是由于疫情因素,人口外出减少,供暖需求的加大所导致,对比模型在长春、北京2市的预测精度可以看出,PSO-BP模型预测精度最高,其RMSE值相比ARIMA 模型、BP模型在长春和北京2市非疫情期提升31.3%,39.3%和23.1%,42.5%,MAE值提升20.0%,40.8%和23.3%,37.3%;疫情时期RMSE提升25.1%,25.3%和41.2%,71.8%,MAE提升了23.2%,27.0%和45.4%,72.8%。对比MAPE的值可以看出,PSO-BP模型的误差均要小于ARIMA模型和BP模型,且PSO-BP模型在上海、长春、武汉和北京4个城市中,疫情期的数值要小于非疫情期,说明疫情期间PSO-BP模型预测准确度更高。通过4个城市的分析可以看出,PSO-BP模型相较于ARIMA模型和BP模型,RMSE和MAE在疫情期的整体提升数值要优于非疫情期,MAPE在疫情期整体优于非疫情期,则说明在疫情期间PSO-BP模型预测结果准确度更高,模型适用性更优,更加适合疫情时期的城市PM2.5浓度预测工作。
4 结束语
本文探索了上海、长春、武汉和北京4个城市疫情前后2年1月—3月的PM2.5浓度变化规律,综合结果分析,4市均由于新冠肺炎疫情的出现,疫情年的PM2.5浓度相比较非疫情年出现了降低趋势。根据模型在4市对于PM2.5浓度预测的适用性可知,PSO-BP模型在预测结果及精度均优于ARIMA模型和BP神经网络模型,同时通过2个时期的RMSE,MAE,RMSE的值对比分析可知,PSO-BP模型在疫情期间的模型适用性会表现更好。但是由预测结果来看,这3种预测模型的结果对于疫情期间的短期PM2.5浓度预测的精度都还有很大的改进空间,通过预测疫情期间的城市PM2.5浓度变化,能为疫情期间城市空气质量治理提供一些借鉴意义。
