N 阱电阻的单粒子效应仿真*

琚安安 郭红霞 张凤祁 刘晔 钟向丽 欧阳晓平 丁李利 卢超 张鸿 冯亚辉

1) (湘潭大学材料科学与工程学院,湘潭 411105)

2) (西北核技术研究院,强脉冲辐射环境模拟与效应国家重点实验室,西安 710024)

利用计算机辅助设计(technology computer aided design,TCAD)软件针对N 型阱电阻的单粒子效应开展仿真研究,结果表明单个重离子入射到N 阱电阻中会造成器件输出电流的扰动.经过对电阻的工作机理和单粒子效应引入的物理机制进行分析,结果表明重离子在N 阱电阻中产生的电子-空穴对中和了N 阱电阻中的空间电荷区,使得N 阱电阻的阻抗瞬间减小、电流增大,且空间电荷区被破坏的面积越大瞬态电流的峰值越高.随着阱结构中的高浓度过剩载流子被收集,单粒子效应的扰动会消失.但N 阱电阻独特的长宽比设计导致器件中的过剩载流子收集效率低、单粒子效应对阱电阻的扰动时间长.文中还对影响N 阱电阻单粒子效应的其他因素开展了研究,结果表明重离子的线性能量传输(linear energy transfer,LET)值越高、入射位置距离输入电极越远,N 阱电阻的单粒子效应越严重.此外,适当缩短N 阱电阻的长度、提高阱电阻的输入电压、降低电路电流可以增强其抗单粒子效应表现.

1 引言

随着航天技术和半导体技术的发展,越来越多的电子元器件被应用到航天电子系统中.宇航级电子元器件是航天电子系统的第一优先级选择,这类元器件针对空间应用背景进行了加固设计,有较高的在轨运行可靠性,但是价格昂贵、性能落后、可供选择的型号较少[1].为了满足日益增长的空间任务需求,高性能、低成本的商用电子元器件逐渐应用于空间环境中[2].然而,空间中存在大量的高能粒子及射线,它们会对电子元器件产生辐射效应,从而影响器件的可靠性.尤其近年来,随着摩尔定律的发展,电子元器件的特征尺寸不断缩小,空间辐射环境中的单个高能粒子对其造成的威胁(即单粒子效应)也愈发严重.因此,未经过抗辐射加固设计的商用电子元器件在应用于航天电子系统之前,必须要进行筛选、测试与评估.电子元器件的组成结构非常复杂,其单粒子效应可靠性受其中的短板所限制.例如大规模集成电路中集成了数以万计的基本电路单元,它们对单粒子效应的敏感程度不同,器件的LET (linear energy transfer,LET)阈值是由对单粒子效应最敏感的单元决定的.因此对基本电路单元开展器件级单粒子效应研究,对于提高集成电路整体的抗单粒子效应能力具有重要意义,目前已有多种基本电路组成单元表现出对单粒子效应的敏感性,如NMOS晶体管[3]、VD MOS 晶体管[4]、纳米体硅鳍形状晶体管[5]、绝缘体上硅晶体管[6]等.从这些研究对象可以看出,目前对于单粒子效应的关注多集中于后摩尔时代的晶体管等有源器件,而很少针对基本的电阻、电容器等无源器件,然而它们在电子系统中同样不可或缺.

在一项关于商用存储器的单粒子效应试验研究[7]中,发现位于器件外围控制电路中的集成N 阱电阻(如图1(a)所示)才是对单粒子效应最敏感的单元,其敏感程度甚至超过晶体管.因此,N 阱电阻的单粒子效应同样值得被关注.N 阱电阻在模拟电路和混合信号电路中扮演着重要的角色,常见的应用模块有数模转换电路[8]、静电放电(electrostatic discharge,ESD)保护电路[9]、恒定电流源电路[10]等.现有针对集成电阻的研究多集中于器件本身的电学特性和电路应用,而忽视了对器件辐照效应的关注.如1997 年,Booth 和McAndrew[11]研究了三端扩散电阻的电阻值;2006 年,Singh 和Roy[12]计算了N 阱电阻的电阻值;2007 年,李月影等[13]通过建立SPICE 模型研究了高压阱电阻的欧姆特性;2009 年,石晓峰等[14]研究了N阱扩散电阻在电应力下产生的潜在损伤;2010 年,Srinivasan 等[15]研究了N 阱电阻中的低频噪声特性;甚至在2018 年,罗捷等[16]提出一种利用电阻作为静态随机存储器(static random access memory,SRAM)辐射加固的应用方法.但是针对N 阱电阻的单粒子效应一直缺乏报道.

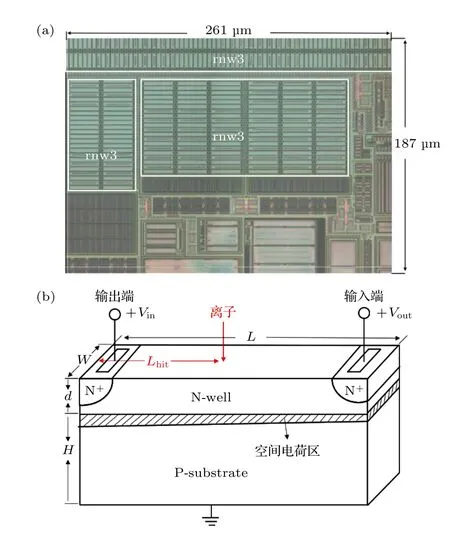
图1 N 阱结构示意图 (a)位于一款存储器外围电路中的N 阱电阻,图中的rnw3 表示三端N 阱 电阻;(b) N 阱 电阻的三维结构示意图Fig.1.Structure diagram of the N-well resistor: (a) An Nwell resistor located in a memory peripheral circuit,rnw3 in the figure represents a three terminal N-well resistor;(b) the three-dimensional structure of N well resistor.

由于试验[7]中发现的N 阱电阻集成在其他电路中,单粒子效应对它产生的影响只能通过整体电路的响应来体现,因此较难从试验上开展针对N阱电阻的单粒子效应研究.本文通过TCAD Sentaurus 仿真工具对N 阱电阻的单粒子效应进行了仿真计算,确定了单个N 阱电阻的单粒子效应规律,从内部过剩载流子的产生、运动及收集过程揭示了器件的单粒子效应机理,并在此基础上对其单粒子效应敏感因素开展了研究,提出了抗单粒子效应建议.

2 模型建立与校准

集成电路设计中有多种常见的集成电阻如多晶硅电阻、金属电阻、阱电阻等等,它们的电学参数(方阻、温度系数和电压系数)不同,各自的优缺点明显.多晶硅电阻精度较高,电阻值对温度和电压的敏感性较小,但其方阻较小.金属电阻是所有集成电阻中方阻最小的电阻,通常用它来做其他电阻无法完成的小电阻.阱电阻受温度、电压、光照、辐射因素影响较大,它的优点在于具有较高的阻抗,达到同样的电阻值所需要的电路版图面积小,因此阱电阻通常被应用于需要高电阻值的电路中.阱电阻有N 阱电阻和P 阱电阻两种,本文以试验[7]中发现的N 阱电阻为研究对象进行说明.N 阱电阻的结构示意图如图1(b)所示,由P 衬底、N 阱以及输入端和输出端的电极构成,P 型区和N 型区之间形成热平衡PN 结.工作时电流从器件输入端流入从输出端流出,P 衬底接地.

根据图1(b)中电阻的结构示意图,分别建立了N 阱电阻的二维和三维器件模型,如图2 所示.在实际的集成电阻中,电阻两端通过金属电极(通常为铝)给电阻施加偏置,金属电极与硅材料形成欧姆接触,接触可视为一个纯电阻,整个电阻为电极接触电阻和N 阱电阻组成的串联电阻总和.为了简化模型,金属材料并未添加在电极上.模型由硅材料构建,分别对衬底区域和阱区域进行了均匀的P 型掺杂(硼掺杂)和N 型掺杂(磷掺杂).图2中三维模型的建立是为了对试验中发现的三维电阻的单粒子效应进行定量地计算仿真,为了保证计算精度,模型中的网格划分必须细密,这导致三维模型中的节点众多,需要大量的仿真时间.因此建立了二维器件模型,二维模型的计算速度较快,虽然仅考虑了两个维度的因素,无法定量计算器件的实际工作结果,但在这两个维度内可以定性地揭示N 阱电阻的单粒子效应机理.

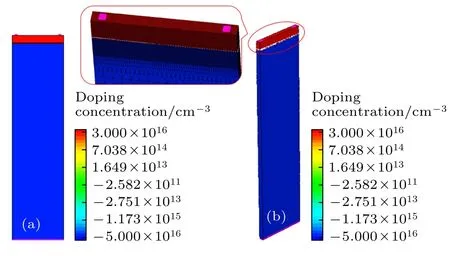
图2 N 阱电阻TCAD 模型示意图 (a)二维模型;(b)三维模型Fig.2.The diagram of N well resistor TCAD model: (a) Twodimension model;(b) three-dimension model.

在建立模型之后,需要对模型的网格划分进行优化来保证模型的准确性和运行速度.通过网格优化发现N 阱结构部分的网格密度对仿真结果的影响较大,而P 衬底部分的网格密度对仿真结果影响较小,因此N 阱部分需要细密的网格划分以确保计算精度,而衬底部分的网格划分可适当放宽以提高计算速度,节约计算时间,最终优化后的三维模型网格划分如图2(b)中的左上角所示.二维模型的网格划分策略同样如此,图中并未再次展示.

为了验证上述网格优化的合理性和模型的准确性,对比了本文模型和其他参考文献中N 阱电阻的电阻值.本文模型的电阻值是基于欧姆定律计算得到,具体操作为在输入端施加一个逐渐增大的电压,固定模型输出端的电压为零,观察输出端电流随输入电压变化的情况,其结果如图3 所示,在电压较小的情况下,输出端的电流随着输入端电压的提高线性增大.文献[11]中利用Matlab 工具根据N 阱和P 衬底之间空间电荷区的厚度精确计算了N 阱电阻在不同掺杂浓度、不同尺寸下的一系列电阻值,而本文则基于欧姆定律同样计算了不同掺杂浓度和不同尺寸下的模型电阻值.表1 中展示了本文模型的电阻值和文献[11]中电阻值的对比情况.从表1 可以看出,尽管仿真工具和计算原理不同,但得到的电阻值表现出良好的一致性,这验证了本文三维模型的准确性.注: 输入电压为3 V,N阱和P衬底的掺杂浓度为5×1016cm3,长度为100 µm.

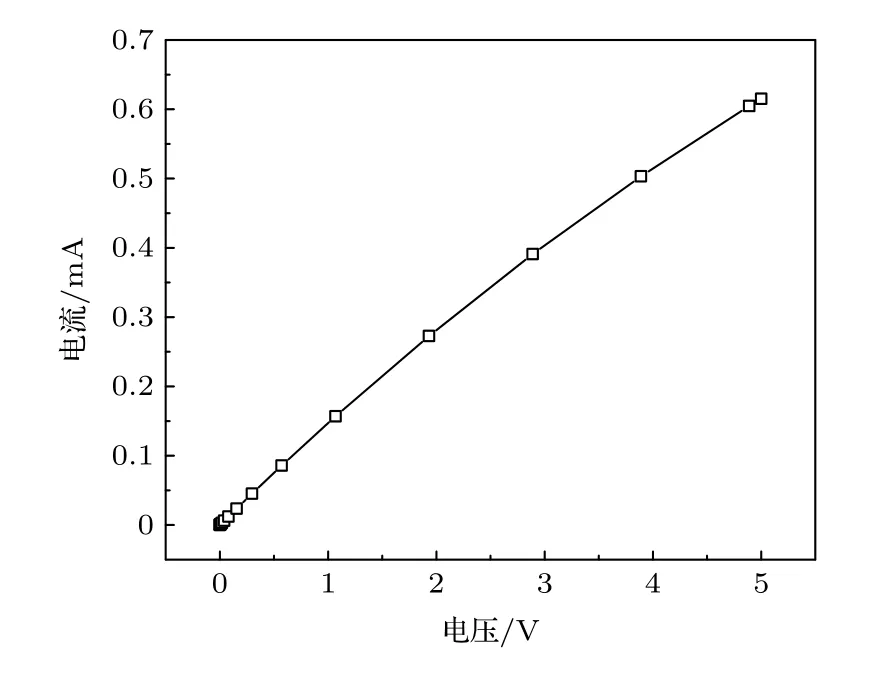
图3 N 阱电阻输出电流随输入电压的变化情况Fig.3.The output current versus the input voltage of the N-well resistor.

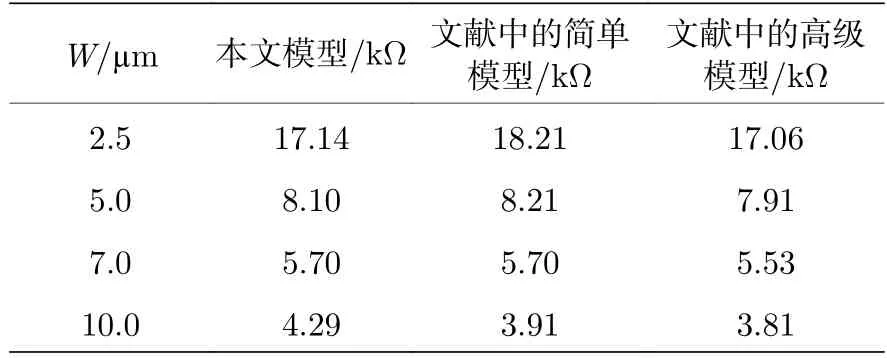
表1 本文模型电阻值与文献[11]中模型电阻值的比较Table 1.The comparison of calculated resistance values in this paper and results in Ref.[11].

3 阱电阻的单粒子效应及其机理分析

在模型校准之后,为了使仿真研究更具有现实意义,模型中尽量采用了试验中发现的N 阱电阻实际参数.电阻的长和宽可以在电子显微镜下通过直接测量得到,而实际的掺杂浓度较难测量,因此在仿真中通过不断调整模型中的掺杂浓度,最终选用的掺杂浓度参数可使模型电阻值等于单个N 阱电阻的实际值(7.5 kΩ).模型所采用的其他参数如表2 所示,其中所选用的N 阱和P 衬底深度均为半导体中常用的工艺参数[11,17].

表2 TCAD 模型中所使用的具体参数Table 2.Detailed parameters used in TCAD models.

在模型校准阶段,为了简化计算将输出端的电压定义为零.但是在实际的应用过程中电阻两端的电压情况比较复杂,输出端的电压可能为零也可能不为零.如电路中常见的上拉电阻和下拉电阻,其作用就是将不确定的信号保持在高电平(通常为电源电压)和低电平(0 V).因此,为了研究单粒子效应对不同工作状态下N 阱电阻的影响,本节设置了不同的输出端电压.模型的输入电压设为3.3 V,即试验[7]中器件的工作电压,输出电压分别设置为0,1.3,2.3 和3.3 V.然后,从模型表面的中间位置入射一个重离子,观察重离子入射后N阱电阻输出电流的变化.入射重离子选用了试验中所用的86Kr25+离子,该重离子的LET 值为37.6 MeV·cm2/mg,在硅材料中的穿透深度为57.5 µm.三维模型的仿真结果如图4 所示,在离子入射之前N 阱电阻的输出电流稳定在一个特定值,当重离子入射后,输出端出现了一个瞬态电流脉冲.N 阱电阻在不同输出端电压下产生的瞬态电流具体信息如表3 所示.表3 中瞬态电流的积分电荷远比单个重离子在阱结构中电离的总电荷量多,重离子对阱电阻的扰动不仅仅为过剩载流子的收集[18−20].因此接下来根据阱电阻内载流子在重离子入射前后不同时刻内的运动情况对器件的单粒子效应机理进行了分析.

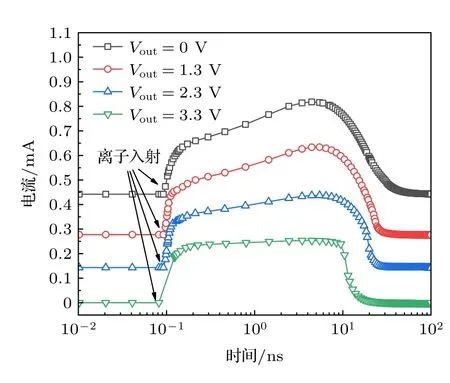
图4 在不同输出电压下,重离子在三维N 阱电阻模型中产生的瞬态电流Fig.4.Ion-induced transient current in the three-dimensional model of N-well resistor under different output voltage.

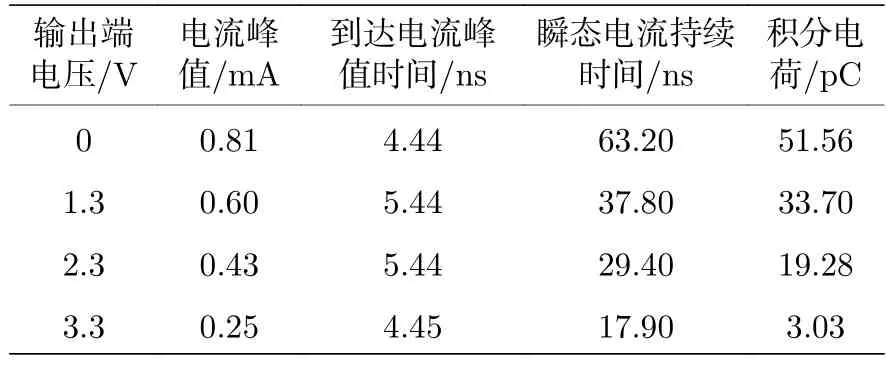
表3 不同输出端电压下,重离子在N 阱电阻三维模型中产生的瞬态电流参数Table 3.Detailed parameters of ion-induced transient current in three-dimension model under different output voltage.

首先讨论输出端电压为3.3 V 的情况,当N 阱电阻的输入和输出电压均为3.3 V 时,N 阱电阻中几乎没有电流通过.由于N 阱结构的电压高于P 衬底电压,PN 结处于反向偏压状态,势垒高度增大,耗尽区(空间电荷区)的宽度增大,如图5(a)所示.由于空间电荷区的电阻远远高于电中性区(即远离PN 结的P 型区和N 型区)[21],这正是阱电阻具有高阻抗的原因.反偏PN 结是N 阱电阻高阻抗的来源,当阱电阻中未形成反偏PN 结时,电阻仅为掺杂硅材料的本征电阻,几乎可以忽略.当重离子入射到N 阱电阻后,沿着其入射径迹在硅材料中电离出大量电子-空穴对.这些电子-空穴对的浓度远高于N 阱的掺杂浓度,重离子径迹附近的耗尽层被中和而消失,如图5(b)所示.耗尽层的消失使电阻阻抗瞬间降低、电流迅速增大.随着重离子引入的非平衡载流子在横向径迹内漂移、扩散,被中和的耗尽层面积逐渐增大、输出电流也进一步增大,如图5(c)所示.最后,随着N 阱结构中过剩载流子的收集,载流子的浓度逐渐降低、耗尽层逐渐恢复,如图5(d)所示,输出电流也逐渐降低直至恢复至正常值.

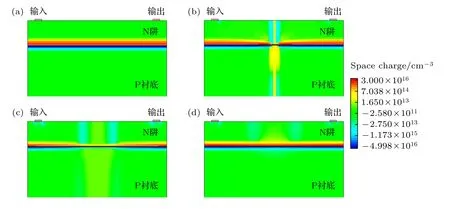
图5 输出电压为3.3 V 时,不同时刻内N 阱电阻内空间电荷区分布 (a) 0 ns;(b) 0.1 ns;(c) 0.6 ns;(d) 5 nsFig.5.When output voltage of model is 3.3 V,the space charge distribution in N well resistor at : (a) 0 ns;(b) 0.1 ns;(c) 0.6 ns;(d) 5 ns.

从表3 中得知,当输出端电压为3.3 V 时,单粒子效应在三维模型中产生的瞬态电流持续时间为17.90 ns,电流峰值为0.25 mA,积分电荷为3.03 pC.然而当输出端电压降低为0 V 时,单粒子效应产生的瞬态电流持续时间、电流峰值及积分电荷分别增至63.2 ns,0.81 mA 和51.56 pC,重离子入射对N 阱电阻产生的影响显著恶化.为了揭示这种现象背后的物理机制,在二维模型中分别提取了不同时间内,深度为2 µm 处的位置上电场强度随N 阱电阻长度分布的情况,结果如图6 所示.当输出端电压和输入端电压相同时(3.3 V),在重离子入射之前(t=0 时),N 阱结构在长度方向上不会产生电场,如图6(a)中的黑色曲线所示.重离子在0.05 ns 时刻入射到N 阱电阻中,当时间为0.1 ns 时,重离子在其入射径迹内产生了大量的电子-空穴对,电场强度增大.电子-空穴对浓度沿着离子入射径迹半径方向逐渐降低、电场强度也随之降低,由于86Kr25+离子径迹中心部分的能量密度低,电场强度在径迹中心位置(L为12.5 µm 处)出现了下凹.最后随着过剩载流子的收集过程,N 阱结构中的横向电场强度逐渐下降,分别图6(a)中t=0.6 ns 和t=5 ns 时的电场分布所示,最终电场强度会降为零.

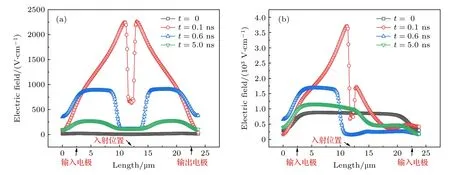
图6 两种不同电压条件下,N 阱结构中深度为2 µm 处的位置上横向电场强度在不同时刻的分布情况 (a) 输出端电压为3.3 V;(b) 输出端电压为0 VFig.6.The distribution of transverse electric field in N well structure at depth of 2 µm location: (a) Output voltage is 3.3 V;(b) output voltage is 0 V.

当输出端的电压与输入端电压不相同时,N 阱结构在长度方向产生了电压降.以输出端电压为0 V 的状态进行说明,N 阱结构中电场强度随长度的分布如图6(b)中的黑色曲线所示,电场方向由输入端指向输出端.重离子入射N 阱电阻后,产生高浓度过剩载流子.由于输入端电场的影响,重离子入射径迹两端的电子不再对称分布,径迹左侧的电子浓度高于右侧,进而导致径迹左侧的电场强度显著高于右侧的电场强度,如图6(b)中时间为0.1 ns 的红色曲线所示.最后,随着N 阱结构中过剩载流子的收集,电子浓度降低,电场强度随之降低.在完全恢复至重离子未入射的状态之前,径迹左侧的电场强度始终高于右侧的电场强度,如图6(b)中时间为0.6 ns 和5.0 ns 时的电场分布曲线所示.

N 阱结构中横向电场的改变显著影响了重离子产生的过剩载流子的收集过程.当N 阱结构中无横向电场(即输出端电压为3.3 V)时,重离子产生的载流子在长度方向沿着入射径迹对称分布,径迹左侧电子向输入端漂移,径迹右侧电子向输出端漂移,整个载流子的收集过程(即瞬态电流的持续时间)仅需要17.90 ns (表3).当输出端电压为0 V时,在重离子入射前,N 阱结构中的电子在输入端电场的作用下向输入端漂移,电流方向从输入端指向输出端.在靠近输入电极的位置电场强度增大,电子的移动速度随之增大,如图7(a)所示.当重离子入射产生高浓度载流子后,N 阱结构中的电场强度增大,电子的漂移速度也随之增大.N 阱结构中电子漂移速度的变化和图6 中电场强度的变化情况保持一致,重离子入射径迹左侧的电子漂移速度始终高于右侧的电子.当重离子入射径迹右侧的电场低于重离子入射前的电场时(如图6 中t=0.6 ns 和t=5.0 ns),径迹右侧的电子速度明显低于左侧,如图7(c)—(e)所示.这导致径迹右侧电子的收集效率远低于径迹左侧,过剩载流子的收集过程需要花费更多的时间.从表3 中可知,当输出电压为0 V 时,载流子的收集过程需花费63.2 ns,但是图4 中Vout=0 V 的瞬态电流在4.44 ns 就达到峰值,后续58.76 ns 的时间内输出电流均处于下降趋势.这是由于输出电流的上升阶段对应着N 阱电阻中耗尽层的破坏过程,而输出电流的下降阶段则对应着耗尽层的恢复过程.如图8 所示,在重离子入射N 阱电阻后,提供高阻抗的空间电荷区被破坏.随着重离子引入的非平衡载流子漂移、扩散,被中和的空间电荷区区域逐渐增大,输出电流也进一步增大.输出电流在4.4 ns 达到峰值,此时除了输入端附近,N 阱电阻中的耗尽层几乎完全消失,如图8(d)所示.这是由于输入端附近的电场较强、电子的收集效率高、过剩载流子浓度低导致.此后,随着N 阱结构中过剩载流子的收集,空间电荷区逐渐恢复,N 阱电阻中的阻抗逐渐增大、输出电流也逐渐降低,最终恢复至正常值.

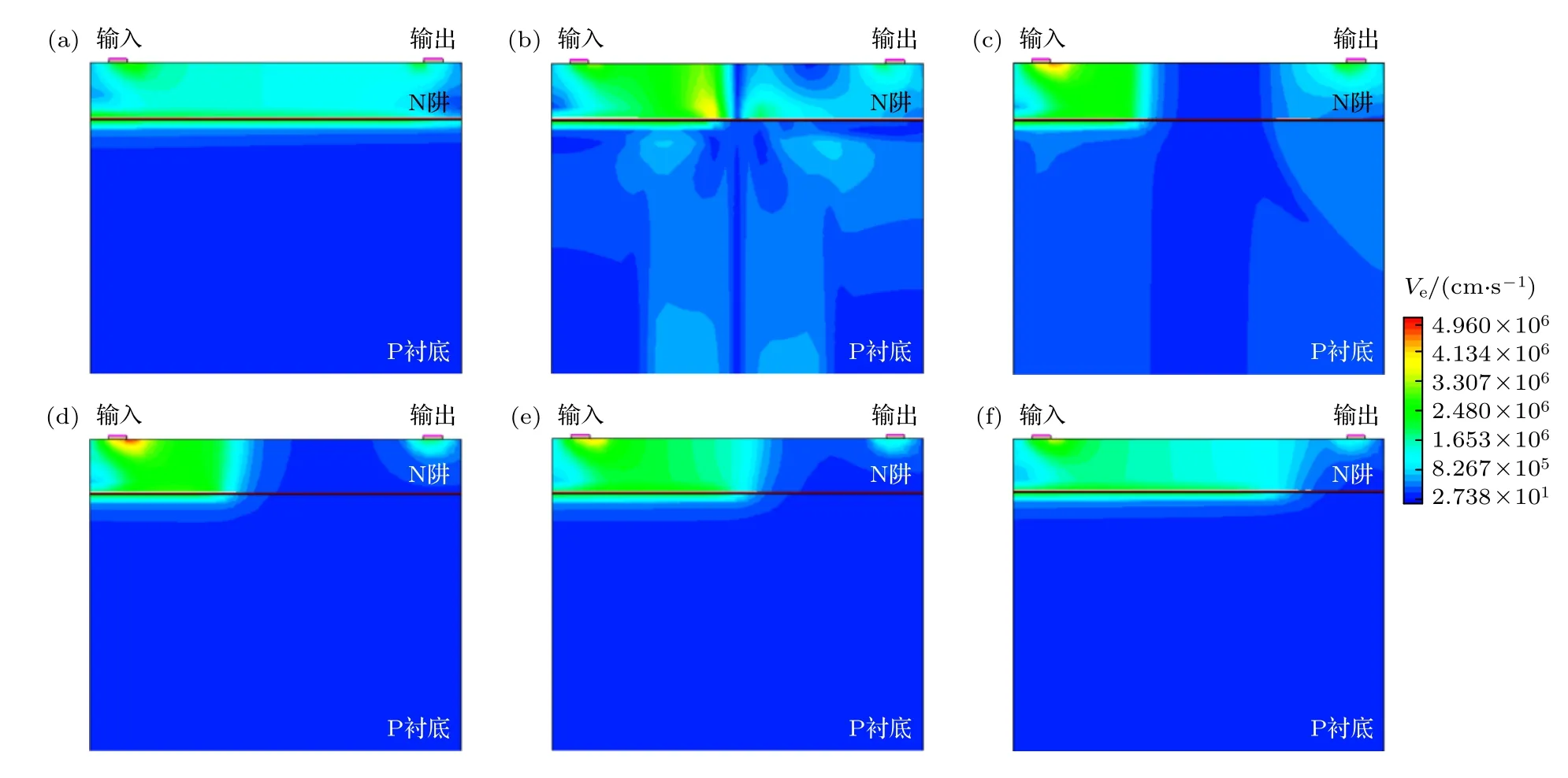
图7 输出电压为0 V 时,不同时刻内N 阱中电子速度分布 (a) 0 ns;(b) 0.1 ns;(c) 0.6 ns;(d) 5 ns;(e) 15 ns ;(f) 30 nsFig.7.When output voltage is 0 V,the distribution of electron velocity in N well structure at: (a) 0 ns,(b) 0.1 ns,(c) 0.6 ns,(d) 5 ns,(e) 15 ns and (f) 30 ns moment.

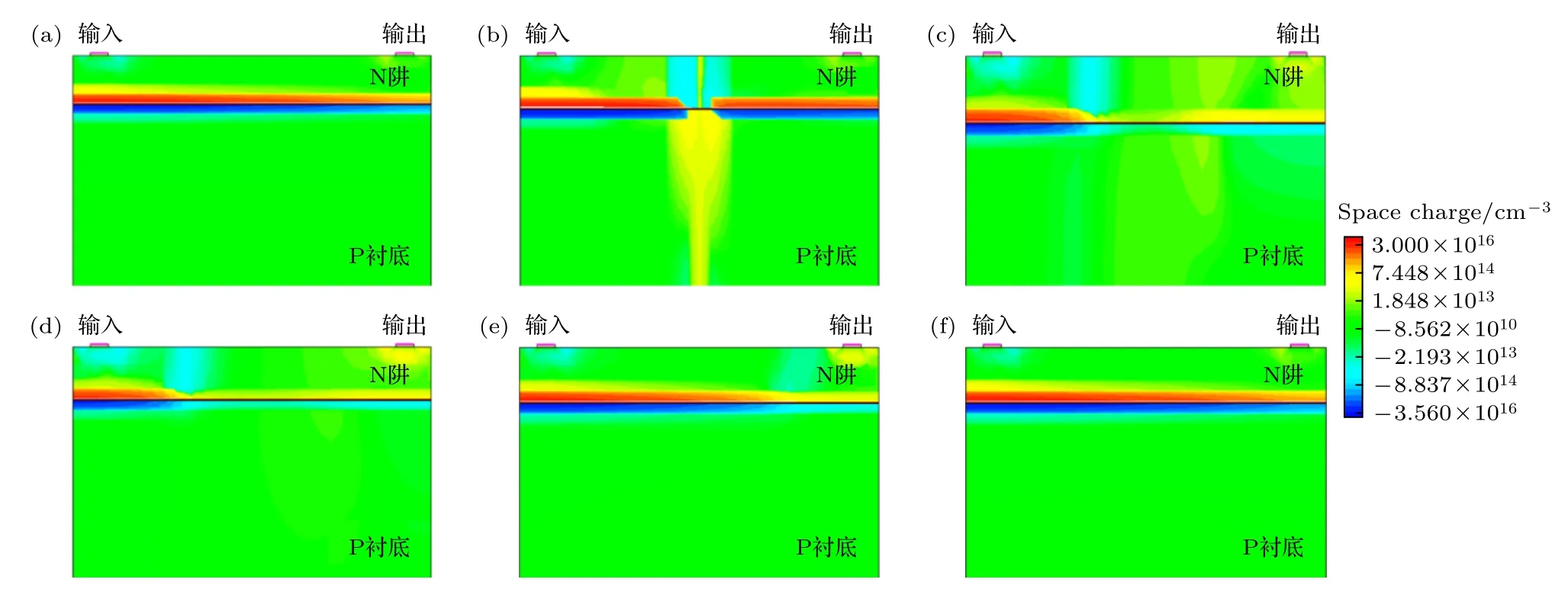
图8 输出电压为0 V 时,不同时刻内N 阱电阻中空间电荷区的变化 (a) 0 ns;(b) 0.1 ns;(c) 0.6 ns;(d) 5 ns;(e) 15 ns ;(f) 30 nsFig.8.When output voltage is 0 V,the change of space charge region in N well structure at (a) 0 ns,(b) 0.1 ns,(c) 0.6 ns,(d) 5 ns,(e) 15 ns,(f) 30 ns moment.

重离子入射到其他常见的晶体管[1−4]中也会使器件产生瞬态电流,但是这些器件中瞬态电流的持续时间仅为数纳秒,重离子在N 阱电阻中产生的瞬态电流持续时间远超过有源器件和数字电路[22]中的瞬态电流.这与N 阱电阻的长宽比有关,在电路设计中集成电阻的电阻值R由其尺寸和电阻率ρ所决定,如(1)式所示:

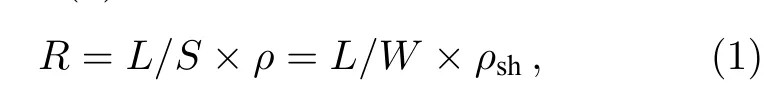
式中,L,W,S分别为电阻的长、宽和表面积,ρsh为集成电阻的方阻.由此可见,为了得到更大的电阻值,除了选用方阻大的电阻外,较大的长宽比也极为重要,所以集成电路设计中的电阻通常会设计成狭长的长方体,如图1(a)所示.但过大的长宽比一方面会增大过剩载流子的漂移距离,另一方面会降低N 阱结构中的电场强度.如在文献[3,23]中器件内的电场强度在105—106V/cm 范围内,而本模型中的电场强度仅在103—104V/cm 内,这使得过剩载流子只能以较低的漂移速度被收集.因此,单粒子效应对N 阱电阻产生的影响要大于在其他器件中的影响.

上述分别讨论了当输出电压为0 V 和3.3 V时,N 阱电阻中的单粒子效应机理,输出电压介于二者之间的瞬态电流及物理过程也介于上述两种情况之间.输出电压为0 V 是N 阱电阻对单粒子效应最恶劣的工作状态,因此,集成电路中输出端接地的下拉电阻受单粒子效应的影响最大.此外,当一个固定值的电阻接入电路后,在输入端电压固定的情况下输出端的电压实际上是由电路中的电流决定的.电路中的电流增大后,电阻中产生的电压降也随之提高、输出端的电压降低.因此,从上述研究结果中也可以看出单粒子效应对应用于高电流电路中的N 阱电阻产生的影响更大.

4 阱电阻单粒子效应敏感参数

从上述N 阱电阻的单粒子效应机理可以看出,重离子在N 阱电阻中产生的电流脉冲与N 阱电阻的几何尺寸、电场的强度、入射重离子电离出的载流子浓度及产生位置密切相关.因此接下来在三维模型中分别对器件的瞬态电流与重离子入射位置的依赖性、重离子LET 值的依赖性、器件尺寸和输入电压的依赖性进行了研究,并提出了一些抗单粒子效应加固建议.需要补充的是,模型输出端的电压固定为0 V,让N 阱电阻处于最恶劣工作条件下进行讨论.

4.1 入射位置的依赖性

重离子的入射位置决定了N 阱结构中非平衡载流子的产生位置,也会影响过剩载流子的漂移距离和电荷收集时间.图4 中的电流瞬态是由86Kr25+离子从N 阱电阻表面的中间位置处入射导致的,当该离子分别从长度为4,8,16,20 µm 的位置入射到N 阱电阻中,得到的单粒子瞬态电流如图9所示.从图9 可知,重离子的入射位置越靠近输入端,器件中产生的瞬态电流峰值越大、脉冲持续时间越短.这是因为高浓度电子-空穴对越靠近输入端,输入端电场对N 阱结构的影响区域越小,即图8(d)中未被中和的耗尽层面积越小,N 阱电阻的阻抗越小、输出电流越大.但是在过剩载流子的收集过程中,电子的漂移距离减小、漂移速度提高、器件内耗尽层的恢复过程加快.在重离子产生的非平衡载流子浓度不变的情况下,电子收集效率提高、瞬态电流的脉冲时间缩短.

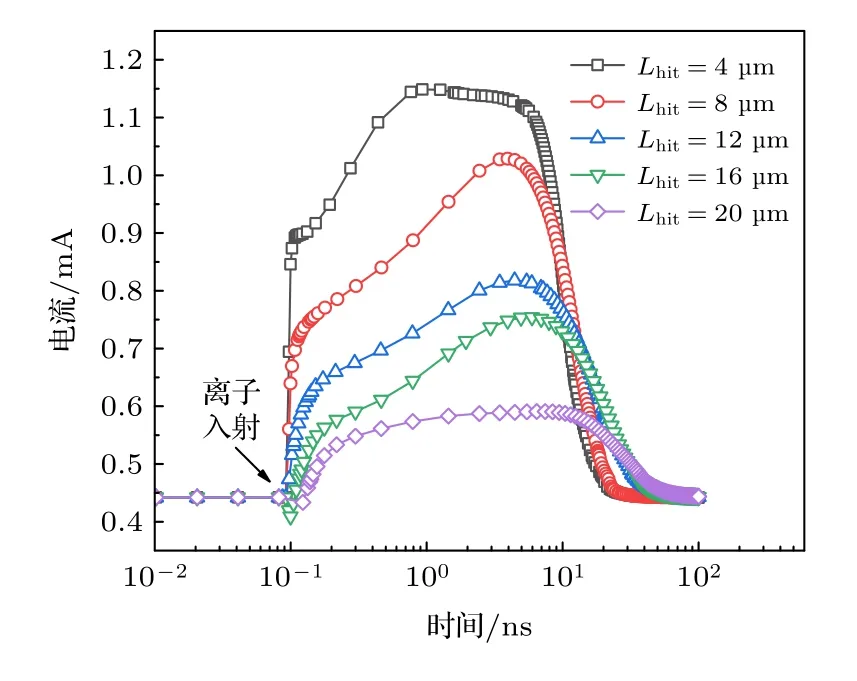
图9 重离子从不同位置入射N 阱电阻产生的单粒子瞬态电流Fig.9.Single event transient current in N-well resistor generated by ion from different incident locations.

4.2 重离子LET 的依赖性

重离子在材料中产生的电子-空穴对浓度是由重离子LET 值和入射深度决定的,由于N 阱电阻的阱深较浅,在不考虑金属布线层的阻挡情况下,大部分重离子均能穿透N 阱结构,因此主要针对重离子的LET 值进行研究.为评估N 阱电阻在单粒子效应试验中常见重离子辐照下的表现,仿真中采用地面模拟试验装置中常用的5 种不同表面LET值的重离子,分别为1.73 MeV·cm2/mg 的12C6+、4.06 MeV·cm2/mg 的19F9+、11.8 MeV·cm2/mg 的32S10+、18.7 MeV·cm2/mg 的40Ca9,13+、65.6 MeV·cm2/mg 的127I15+.重离子从器件中间位置入射,输出电流结果如图10 所示,LET 值越高的重离子在硅材料中电离出的载流子浓度越高,耗尽层被破坏的面积越大,瞬态电流的峰值越高.另外,高浓度过剩载流子被收集所花费的时间越长,瞬态电流的持续时间也随之增加.

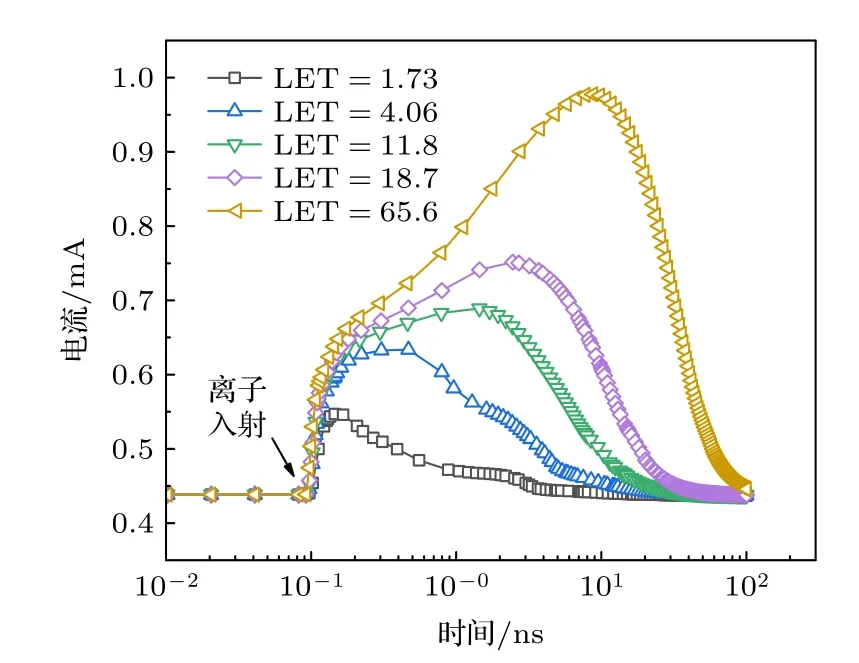
图10 不同LET 值的重离子在N 阱电阻中产生的瞬态电流Fig.10.Single event transient current in N-well resistor generated by ions with different LET values.

4.3 几何尺寸和工作状态的依赖性

以上探讨了入射离子参数对阱电阻单粒子效应的影响,这些因素是由器件的外部应用环境所决定.为了探讨是否可以从阱电阻本身的设计及应用上改善器件的单粒子效应性能,接下来在入射离子不变的情况下,开展了针对阱电阻自身几何尺寸、输入电压等因素对其单粒子效应影响的研究.

在几何尺寸方面,从(1)式可知在电路设计中通过改变电阻的长宽比可以获得想要的电阻值.在目前的工艺中阱电阻的宽度已经很小,通常为2 µm,因此更多根据阱电阻的长度设计电阻值.图8 中展示了将长度扩大1 倍后,N 阱电阻对入射重离子的响应.86Kr25+离子仍然从器件表面中间位置入射,其参数与第3 节工作的描述相同,图8 中的单粒子瞬态电流对阱电阻的长度进行了归一化处理.在输入端电压不变的情况下,当电阻的长度扩大1 倍后,电阻值增长1 倍、单位长度上的稳态电流降低1/2.为了体现重离子入射对器件电流造成的扰动程度,定义瞬态电流的峰值与稳态电流的比值为扰动因子,扰动因子越大表明重离子导致的瞬态峰值电流超过稳态电流的程度越大.图11 中的结果表明N 阱电阻的长度扩大1 倍后,瞬态电流的扰动因子从1.84 增大到2.46.此外由于长度增加,重离子产生的载流子被输运到输入端的距离增加,载流子的收集过程更加缓慢.对重离子在电阻中产生的瞬态电流进行积分后,得到长度为24 µm 的N 阱电阻在86Kr25+离子从中间位置入射后得到的积分电荷为7.28 pC,而长度增大1 倍后器件内得到的积分电荷增大值17.19 pC.因此尽管增加N 阱电阻的长度可以提高电阻值,但其单粒子效应敏感性也随之增大.单粒子效应对N 阱电阻造成的扰动(无论是电流峰值的扰动还是持续时间的扰动)都随器件长度的增大而提高.出于抗单粒子效应的考虑,在版图设计中阱电阻的长度不宜过长.

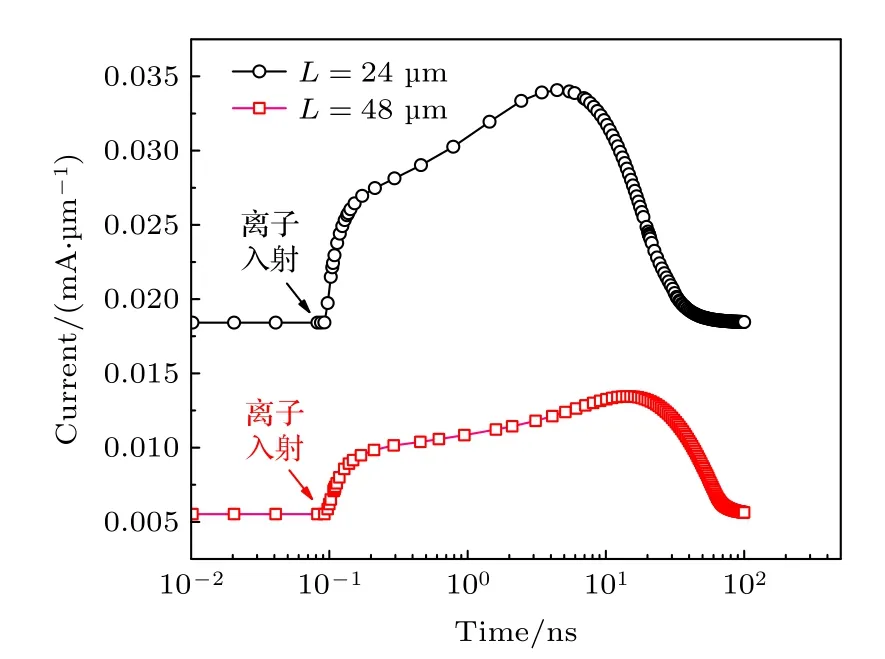
图11 不同长度的N 电阻中产生的归一化单粒子瞬态电流Fig.11.Normalization single event transient current generated in N-well resistors with different lengths.

图12 中展示了在不同输入电压下N 阱电阻单粒子瞬态电流的对比,在输出端电压不变的情况下,器件中的电流随输入端电压的提高而增加.当输入电压为1 V 时,瞬态电流的扰动因子为3.1,积分电荷为11.98 pC.当输入电压增长至5 V 后,瞬态电流的扰动因子降至1.75,积分电荷降低为8.71 pC.该结果表明提高输入端电压后,单粒子效应对N 阱电阻的影响明显降低.这是因为输入电压提高后,阱结构内的电场强度增加、过剩载流子的收集效率提高、耗尽层的恢复时间缩短导致.因此,当N 阱电阻应用于驱动能力低的电路中,器件的单粒子效应敏感性提高.

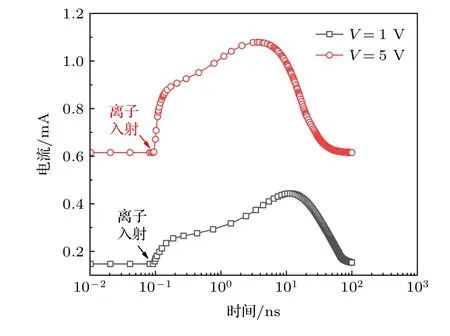
图12 不同输入电压下的N 阱电阻产生的单粒子瞬态电流Fig.12.Single event transient current generated in N-well resistors under different input voltage.

5 结论

本文基于试验中的发现,指出N 阱电阻作为电路系统中的常用组件对单粒子效应尤为敏感.N 阻电阻依靠反向偏压下阱与衬底之间形成的空间电荷区为电路提供大阻抗,但单粒子效应在材料电离出的高浓度载流子会中和N 阱电阻的空间电荷区,导致电阻的阻抗降低,器件中出现瞬态电流.当N 阱电阻应用于低电流的电路中,单粒子效应对其产生的影响明显增大.输入端接电源电压、输出端接地是N 阱电阻对单粒子效应最恶劣的工作状态.由于N 阱电阻采用较大的长宽比设计导致器件中的电场强度低、非平衡载流子收集效率低,最终使得N 阱电阻中产生的瞬态电流持续时间远大于重离子在晶体管等其他有源器件中产生的电流.此外,重离子从N 阱电阻中的不同位置入射对器件造成的影响不同,从靠近输入端的位置入射,耗尽层的破坏程度最严重,但是电荷收集效率更高、载流子达到平衡状态的时间更短,表现在瞬态电流上为高电流峰值、低脉宽.不同LET 值的重离子对器件输出电流的扰动程度也不同,低LET值的重离子在器件内产生的载流子浓度低,瞬态电流的持续时间和峰值也随之降低.从阱电阻的几何尺寸和输入电压对其单粒子效应开展研究,发现器件长度的增加固然会提高电阻值,但其单粒子效应敏感性也随之增加,因此在抗辐射电路设计中应避免使用过长的阱电阻.此外,当N 阱电阻应用在驱动能力高的电路中,瞬态电流的峰值和持续时间都会降低,单粒子效应的扰动减弱.总而言之,虽然N 阱电阻的结构简单但其应用广泛,N 阱电阻的单粒子效应值得更多关注,在针对辐射环境应用背景进行抗辐射集成电路设计时,N 阱电阻的使用仍然需要慎重.