基于形貌优化的动力电池上盖模态优化

刘学荣，童 辉，冯 刚，苏国栋

基于形貌优化的动力电池上盖模态优化

刘学荣，童 辉，冯 刚，苏国栋

（新兴际华应急产业研究院，北京 100070）

动力电池上盖模态直接影响到整车噪声、振动与声振粗糙度（NVH）性能及结构耐久性能，为了提升动力电池上盖模态性能，通过形貌优化方法对上盖进行了结构优化。基于求解器MSC.Nastran对动力电池上盖的模态进行了分析，根据分析结果，利用形貌优化法对重点关注的第1阶模态进行了优化，通过改变上盖结构特征，使得上盖第1阶模态由9.6 Hz提升至25.61 Hz。结果表明，形貌优化技术能够有效提升动力电池上盖模态性能，为动力电池上盖优化设计提供了参考。

动力电池；上盖；模态；形貌优化

新能源汽车技术发展突飞猛进，动力电池作为新能源汽车及其重要的部件之一，对整车性能有着至关重要的影响。动力电池的结构耐久，噪声、振动与声振粗糙度（Noise, Vibration, Harshness, NVH），耐撞性均对整车性能有重要影响。对新能源纯电动汽车而言，汽车整车质量对续航里程影响较大，汽车整车质量每减少10%，耗电下降5.5%，续航里程增加5.5%[1]。因此，整车开发对电池质量提出了更严苛的要求。

不同形状的动力电池上盖需要有不同的加强筋进行加强。形貌优化在薄板形状的结构寻找最优加强筋均有很好的优势，在产品优化中得到了很好的应用。文献[2]利用形貌优化的方法对列车空调的箱体进行了轻量化设计。文献[3]使用形貌优化技术对邮轮防火墙进行了优化设计，得到了重量轻、强度好的优化方案。

为了提升动力电池上盖模态，避免经验优化带来的时间成本问题，本文利用形貌优化方法对动力电池上盖模态进行了优化。

1 动力电池上盖结构

动力电池的上盖位于动力电池顶部，由薄板结构组成，起到了保护电池内部组件的作用，上盖与箱体框架之间采用螺栓连接。上盖结构如图1所示。

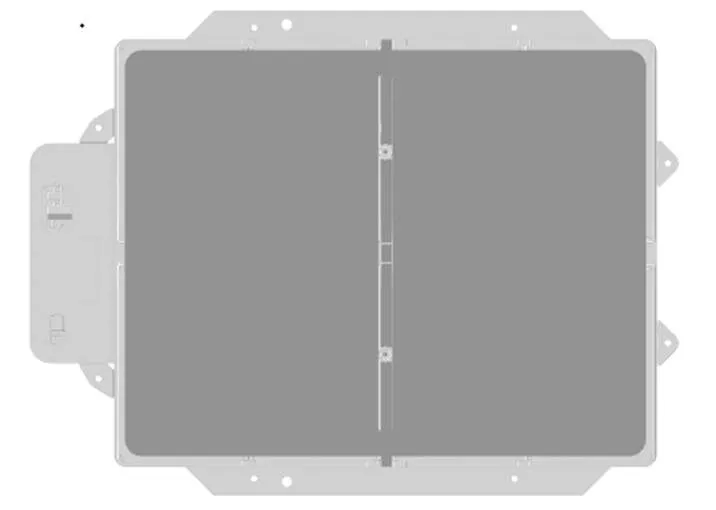
图1 动力电池上盖

2 动力电池上盖有限元模型建立

2.1 网格划分

文中动力电池上盖属于薄板结构，厚度方向尺寸远小于长度方向尺寸，因此，上盖可用壳单元进行划分网格。使用前处理软件对上盖抽取中面，并进行网格划分，单元基本尺寸为10 mm，如图2所示。

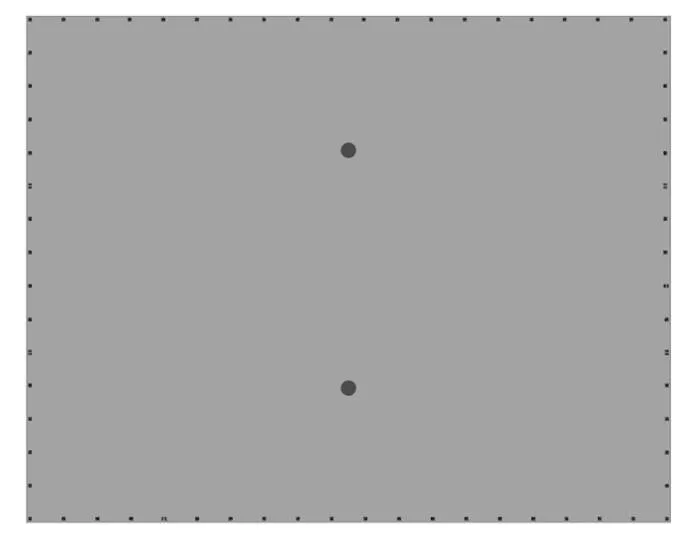
图2 动力电池上盖有限元模型

由于动力电池上盖通过螺栓固定在电池箱体上，螺栓贴合面需要做刚性处理，因此，螺栓安装孔的网格需特殊处理，用一圈深度为5 mm的washer进行划分网格，并用刚性单元rbe2将washer的各个节点连接，用来模拟垫片，使得上盖的连接形式接近真实情况，如图3所示。

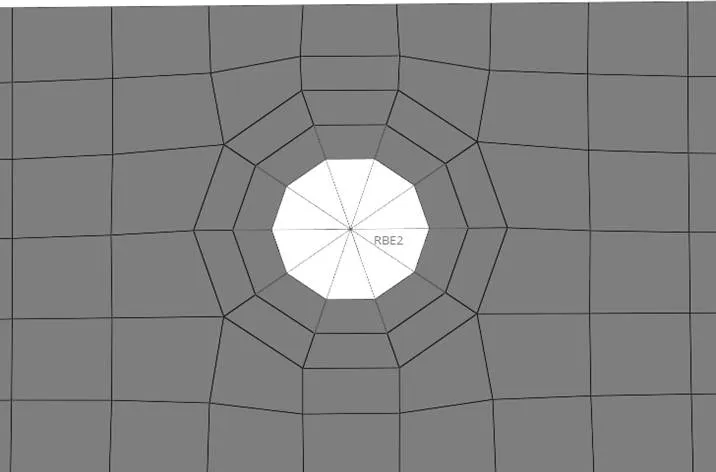
图3 螺栓安装孔建模

有限元模型共有96 889个节点、93 825个单元，其中三角形单元数为6个，四边形单元数为93 690个。

2.2 模型定义

模型定义为壳单元属性，厚度为1.2 mm。上盖的材料为铝合金6063-T6，材料物性参数如表1所示。

表1 材料物性参数

3 上盖模态分析

3.1 模态分析求解方程

模态结构的固有特性之一，用来衡量结构振动性能，每一个结构具有无穷阶模态，对应的每一阶模态具有固定频率和模态振型。模态分析指通过计算或者试验的方法获取模态的固有频率、模态振型。复杂模型可以通过有限元分析方法获取结构模态。动力电池上盖无法通过解析法求得模态，只能借助于有限元方法进行求解。有限元自由振动方程为

(-)=0 （1）

式中，为结构刚度矩阵；为结构质量矩阵。

动力电池上盖为金属材料，其结构阻尼小，由于小阻尼对固有频率的影响小，因此，上盖模态分析可忽略阻尼影响，属于实模态分析。求解式（1）可以得到个特征值λ[4]，从而可以得到固有频率为

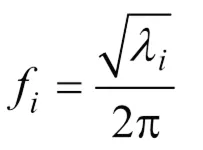
3.2 模态分析结果

对动力电池上盖进行模态分析可以得到上盖固有频率，上盖第1阶模态的高低直接影响到NVH性能及随机振动疲劳可靠性，同时为上盖优化提供理论依据。上盖通过螺栓与电池箱体连接到一起，因此，需要对上盖进行约束模态分析。电池箱体具有刚度高、质量大的特点，根据工程分析经验，上盖模态分析的约束条件为约束上盖各螺栓安装孔的全部自由度。为提高计算效率，采用兰索斯法计算模态，对应的关键字为EIGRL。通过求解器MSC.Nastran求解约束模态分析得到动力电池上盖的前6阶固有频率，如表2所示。

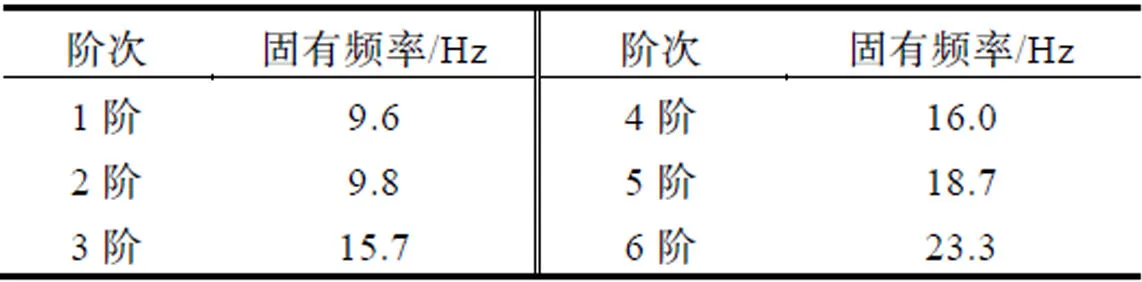
表2 各阶固有频率

第1、2阶模态振型表现为上盖左右两部分垂直于上盖平面方向的振动，第3、4阶模态振型表现为上盖上下左右四部分垂直于上盖平面方向的振动，第5阶模态振型表现为上盖中间部分垂直于上盖平面方向的振动，第6阶模态振型表现为中间部分左右两侧垂直于上盖平面方向的振动。因此，前6阶模态振型均为垂直于上盖平面方向的振动。其中，作为重点关注的动力电池上盖第1阶模态振型图如图4所示。

图4 动力电池上盖第1阶模态振型

4 上盖优化设计

新能源电动车的主要激励来源于汽车行驶过程中的路面激励，根据国标《电动汽车用动力蓄电池安全要求》（GB 38031—2020），其激励频率主要集中在10 Hz～20 Hz之间。为了避振，需要保证动力电池上盖与路面激励频率具有5 Hz的避振频率。因此，上盖模态性能要求不低于25 Hz。通过模态分析结果可以看出，前6阶模态均低于25 Hz，在汽车行驶过程中可能发生共振问题，不能满足性能要求。

4.1 形貌优化理论模型

形貌优化是一种针对薄壳结构加强筋优化布置的优化方法，在不改变厚度的情况下，通过改变薄壳结构上加强筋的位置及加强筋的形状提高薄壳结构的刚度，从而提升模态性能。与拓扑优化不同的是拓扑优化采用的是单元变密度为设计变量，而形貌优化采用的是起筋形状为设计变量[5]。

形貌优化的理论数学模型为

=(1,2,3,4,...,)T（3）

Min=T(e)（4）

式中，e为有限元模型节点在设计空间的位移量，其方向为单元法相或全局坐标方向，0＜e＜；为优化对象的柔度；为在外载情况下节点的位移；(e)为节点移动后的对应模型的刚度；为设计空间内允许节点移动的上限值。

4.2 动力电池上盖变量定义

动力电池上盖四周及中面螺栓安装孔为密封区域，此处需要保持钣金具有完整的平面。因此，将上盖中间区域定义为优化区域，如图5所示。

图5 动力电池上盖优化区域

上盖起筋的高度由设计空间决定，顶部空间需保留与电动车地板之间的间隙，底部空间需保留与模组之间的间隙，根据设计需求，定义起筋高度为5 mm。起筋宽度及起筋角度由单元尺寸及成型工艺决定，定义最小起筋宽度为15 mm，起筋角度为60°。

4.3 动力电池上盖约束及目标定义

形貌优化过程中的变量响应通常为位移、质量、模态、应力等。动力电池上盖主要性能指标为模态，以模态及质量作为响应，以模态作为约束，质量最小作为目标[6]。其中，考虑到形貌优化之后仍需工程化处理，此过程有可能造成优化指标下降，因此，需要对约束值设定一定的裕度。根据工程经验，设置优化约束裕度值为5 Hz，即模态约束值为不小于30 Hz。

4.4 形貌优化

优化求解经过19次迭代后，目标函数收敛，得到各部分节点的变形量，中间区域表示变形量为5 mm，四周区域变形量为0，变形云图如图6所示。

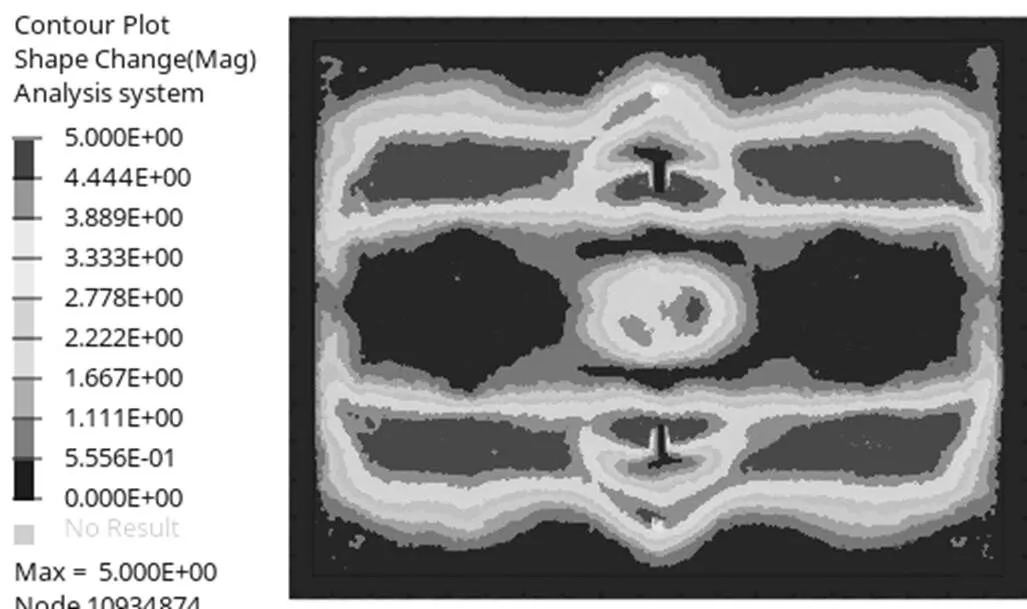
图6 形貌优化变形云图

4.5 结果快速验证

在前处理软件HyperMesh中对形貌优化结果进行快速处理，计算优化后方案的模态，从而快速验证方案可行性。快速验证模型如图7所示。

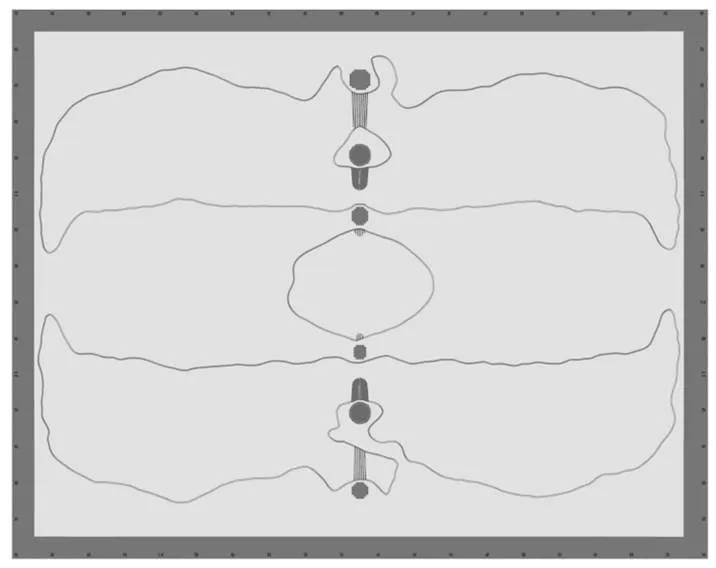
图7 动力电池上盖快速验证模型

经求解计算得到前6阶模态结果，其中第1阶模态为29.6 Hz，满足性能指标要求。其振型图如图8所示。

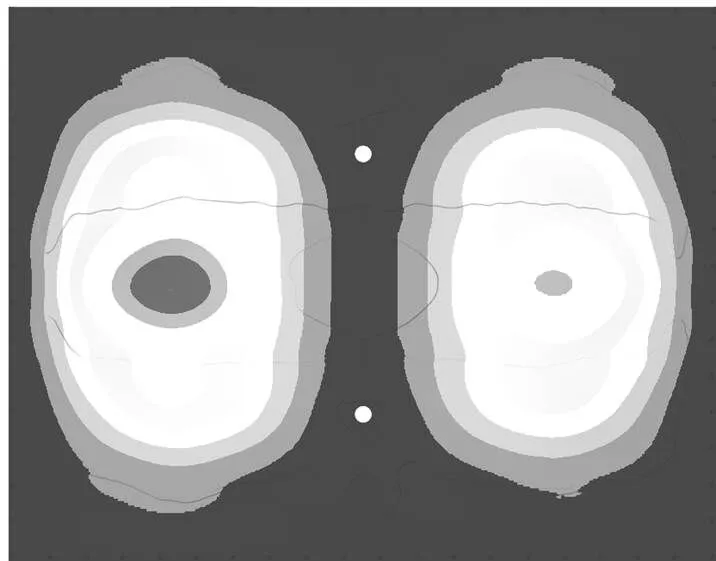
图8 形貌优化结果快速验证振型图

4.6 工程化处理

形貌优化的结果存在一些锐角、断面等容易产生工艺缺陷的问题，无法直接使用形貌优化结果。因此，需要对形貌优化的结果进行工程化处理。将优化结果导出igs格式的几何面，在三维设计软件SolidWorks中对其进行工程化设计，工程化设计过程中主要考虑最小圆角、拔模方向、密封性的要求。工程化结果如图9所示。

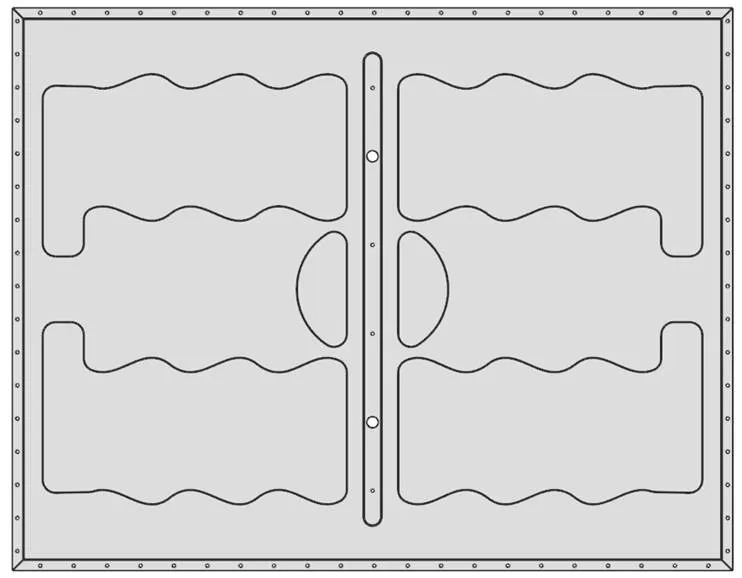
图9 工程化模型

5 优化结果验证

将优化后的几何模型导入到前处理软件中进行网格划分、材料定义、属性定义、求解设置等前处理工。使用求解器MSC.Nastran求解前10阶约束模态，得到各阶模态值。其中前6阶固有频率如表3所示。

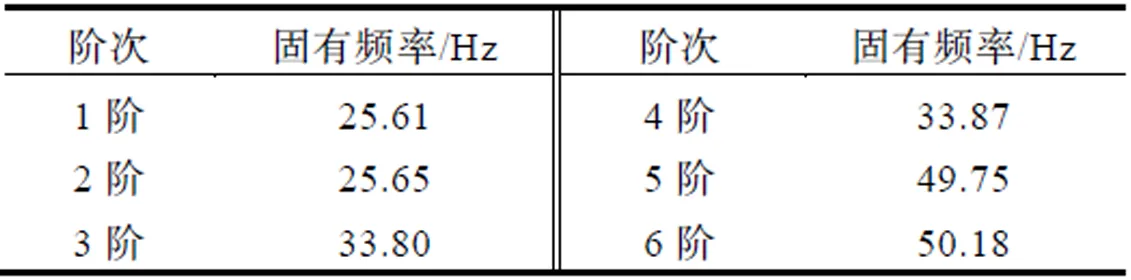
表3 各阶固有频率

其中，第1阶模态固有频率为25.61 Hz，比形貌优化快速验证模型结果低了3.9 Hz，主要是由于工程化之后部分特征移除造成的。优化结构比原始结构提升了16.01 Hz，固有频率提升了167%，有效地提升了固有频率，达到了优化效果。第1阶模态振型图如图10所示。

图10 优化后第1阶模态振型图

为验证仿真优化结果的准确性，使用求解器ABAQUS对同一有限元模型进行模态分析，得到前六阶固有频率，与MSC.Nastran计算结果偏差最大的为第4阶频率，偏差为0.5%。通过两种软件仿真分析结果对比可知，仿真分析结果差异小、仿真精度满足工程需求。ABAQUS仿真计算得到的前6阶固有频率如表4所示。

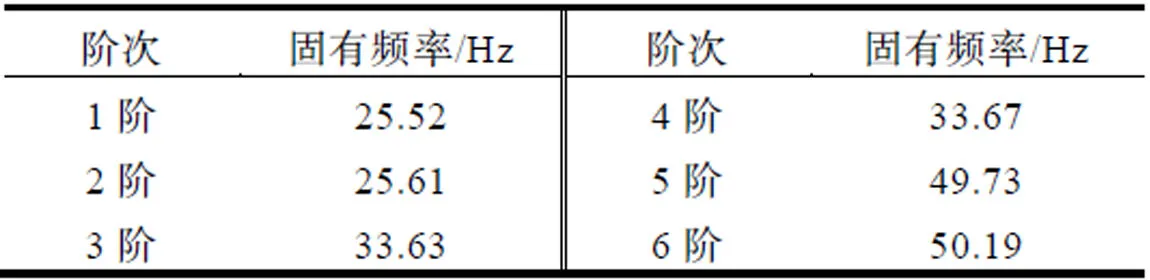
表4 ABAQUS求解所得各阶固有频率

6 结论

本文以动力电池上盖为研究对象，通过模态分析得到了前6阶模态的固有频率和振型。根据动力电池上盖的性能要求，得出原有方案不能满足求解的结论。为满足性能要求，对动力电池上盖进行了形貌优化，根据形貌优化结果对上盖合理起筋，固有频率由9.6 Hz提升至25.61 Hz，固有频率提升了167%，优化后的上盖满足了性能要求，保证产品安全性。

[1] 王品健.纯电动汽车动力电池包箱体结构轻量化设计与优化[D].长沙:湖南大学,2018.

[2] 王枫,曹立达.基于形貌优化的列车空调箱体轻量化分析[J].流体机械,2019,47(5):79-83.

[3] 张帆,杨德庆,邱伟强.基于形貌优化技术的邮轮轻型防火围壁设计[J].上海交通大学学报,2021,55(10): 1175-1187.

[4] 欧贺国,方献军,洪清泉.RADIOSS理论基础与工程应用[M].北京:机械工业出版社,2013.

[5] 洪清泉,赵康,张攀,等.OptiStruct&HyperSsudy理论基础与工程应用[M].北京:机械工业出版社,2013.

[6] 程必良.纯电动汽车电池包结构优化设计研究[D].太原:中北大学,2021.

Modal Optimization of Power Battery Cover Based on Topography Optimization

LIU Xuerong, TONG Hui, FENG Gang, SU Guodong

( Xinxing Cathay Emergency Industry Institute, Beijing 100070, China )

The modal of the power battery cover directly affects the noise, vibration, harshness(NVH)performance and structural durability of the whole vehicle. In order to improve the modal performance of the power battery cover, the cover structure is optimized by using topography optimization method. Based on solver MSC.Nastran analyzed the modal of the power battery cover. According to the analysis results, the first modal that is of great concern was optimized by using the topography optimization method. By changing the structural characteristics of the cover, the first modal of the cover is increased from 9.6 Hz to 25.61 Hz. The results show that the topography optimization technology can effectively improve the modal of the power battery cover, which provides a reference for the optimization design of the power battery cover.

Power battery; Cover; Modal;Topography optimization

TH122

A

1671-7988(2023)03-95-05

10.16638/j.cnki.1671-7988.2023.03.018

刘学荣（1988—），男，硕士，工程师，研究方向为特种装备仿真技术应用，E-mail:liu.x.rong@163.com。