电双层电容孔隙渐变多孔电极电化学特性分析

李泽宇，陈 威

(上海海事大学商船学院，上海 201306)

电化学超级电容器具有充电快、充放电周期长、工作温度范围宽等优点。电化学超级电容的数学模型可以分为三种类型：多孔介质微尺度建模[1-3]、等效电路模型[4-6]和多孔电极理论框架[7-9]。由于多孔电极中的变孔隙结构对电解质中离子的迁移和扩散有很大的影响。因此，许多学者将这种电极结构应用到液流电池和锂离子电池的电极上[10-12]。这种多孔结构化设计使得相应的电化学性能有所提升。

本文基于多孔电极理论框架，将Chen 等[10]提出的新型电极结构布置在多孔电极上，并参考Subramanian 等[13]的研究修正了电解质和固相多孔电极的电导率；考虑到电解质溶液的扩散和迁移来分析多孔电极上的变孔隙结构对电双层电容性能的影响，进一步补充了分级多孔电极的理论研究。通过在电双层电容的电极上采用渐变孔隙结构，模拟分析了其结构对恒流恒压及恒功率下的电化学性能的影响，得到了不同孔隙结构下的恒流充电恒压放电特性，恒功率充电下电双层电流源和电荷密度及恒功率放电下的电流电压特性。

1 物理模型

如图1(a)所示，电双层电容器是由两个活性炭电极、电解质溶液、隔膜等组成，隔膜将两个多孔电极隔开，非水电解质LiPF6溶液充满整个电双层电容器。在电双层中，由于电解液中的阴阳离子可以被稳定地吸附到具有活性材料的多孔电极上，因此，电荷是静电存储的。双电层电容的电荷存储是发生在电极材料上，在界面上没有发生任何的电荷转移。由于在多孔活性炭电极表面上所吸附的带有正负电荷的离子被平衡，从而产生了电容。

图1(b)为电双层电容器几何结构示意图，蓝色区域为具有多孔性的隔膜，里面充满着自由电解质。左右黑色区域是含活性炭的多孔电极，电极孔隙内的溶液是电中性的。沿x轴依次排列的是50 μm 的活性炭电极，25 μm 的隔膜，50 μm的右侧活性炭电极。在充电过程中电解质中的离子向两侧多孔电极扩散和迁移，锂离子在多孔碳电极表面积累，形成双电层；在放电过程中，双电层被中和，其中储存的能量也随之释放出来，从而达到放电的效果。

图1 电双层电容器原理示意图(a)与几何结构示意图(b)

2 数学模型

2.1 模型假设

在模拟分析电双层电容器的电化学特性时，做如下假设：

(1)该模型模拟的是一维的超级电容截面，忽略其长度和高度的边缘效应。

(2)假设正负离子在dq+/dq=dq-/dq=-1/2 上是相等的。

(3)假定电容aC是恒定的。

(4)扩散过程的阻力无作用，忽略扩散阻力。

(5)认为是一维等温的，忽略温度的变化。

(6)当电极厚度为50 μm 时，假定多孔电极理论是有效的，因为输运现象基本上是一维的。

2.2 描述方程和边界条件

有效介质理论考虑了孔隙度和弯曲度对输运参数值的影响。对液相采用了两个唯象方程。首先，离子通过迁移和扩散进行输运，一维通量关系由能斯特-普朗克方程提供：

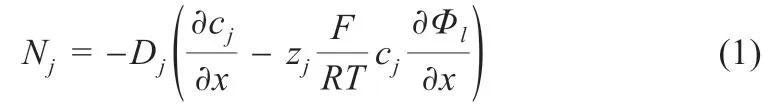
式中：Nj为物质通量；Dj为扩散系数，m2/s；zj为电荷数；F为法拉第常数，C/mol；R为通用气体常数，J/(mol·K)；T为绝对温度，K；cj为浓度，mol/L；Φl为电解质液相电势，V。

采用的第二种关系由于双电层充放电而使物质j远离电极表面的摩尔通量表示为：

式中：j为稀物质种类；C为电容，F；qj为电极表面电荷；Φs为固相多孔电极电势，V。

固相多孔电极采用欧姆定律：

式中：is为固相多孔电极侧的电流，A；σ为固相电导率，S/m。

考虑孔隙率和曲度，定义了多孔电极的有效电导率和有效扩散系数：

式中：ε为孔隙率；τ为曲度。

液相的欧姆定律呈浓度有关的非线性形式：

式中：il为液相电解质侧的电流，A；k为电解质电导率，S/m；t+为电荷转移数。

其中转移数tj与离子扩散系数有关：

电解质的有效电导率与阿奇指数[14]有关：

式中：keff为电解质有效电导率，S/m。

通过能斯特方程计算迁移离子的迁移率：

中性液相中电荷守恒为：

式中：a为比表面积，cm2/cm3。

二元电解质的物质平衡产生的守恒方程：

其中多孔电极处的比表面积与孔隙率可以表示为[15]：

边界条件如下所示。

在左集流体处（x=0）有：

在电极-隔膜边界处（x=LA和x=LA+LS）均有：

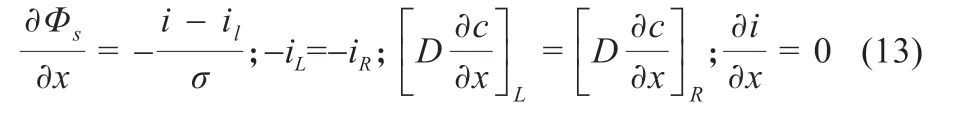
在右集流体处（x=LA+LS+LB）有：

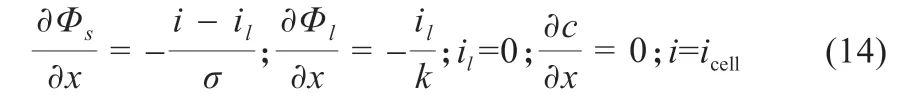
计算中所用参数和负载参数分别如表1 和表2 所示。

表1 计算中所用的参数

表2 负载参数

2.3 模拟计算过程和模型验证

对所建立的模型使用COMSOL Multiphysics5.5 进行求解，其中在电化学模块选择“三次电流分布，Nernst-Plank”，以及使用数学中的事件来模拟由恒电流充电-恒电压放电组成的负载循环。使用全局方程节点计算电流密度，在右侧活性炭多孔电极边界上指定恒功率充电，用静息电位来确定初始值，采用参数扫描法模拟了不同的外加功率和静息电位。选择向后差分公式(BDF)方法用于时间步进器。求解使用的迭代方法是广义最小残差法，相对容差设定为10-4。

网格质量对数值计算的稳定性和准确性尤为重要。本文对模型网格进行了用户控制网格，通过在两侧的多孔电极创建更高分辨率的网格，使计算结果准确稳定。自定义使用三种不同的网格数：普通网格(424 单元)、细网格(536 单元)、较细网格(1 948 单元)。分析结果如表3 所示。

表3 恒电流充电电压范围随网格数变化

结果表明，网格大小质量对模拟结果产生的影响极小，为了节省计算所需的时间，本文采取较细化网格。将25 ℃下恒电流充电和电压实验所得到的电流电压曲线，与数值模拟计算所得到的一个周期内25 ℃下的恒电流电压曲线进行对比。实验数据来自文献[18]。从图2 可以看出，模拟曲线与实验曲线吻合度较高，由于模型建立过程中存在很多假设理想化以及部分物性参数选取有所差异，这个误差是可以允许的，因此验证了模拟的正确性。

图2 电双层电容恒电流电压模拟结果与实验[18]对比(25 ℃，100 A恒流充电，1.4 V恒压放电)

3 结果与讨论

3.1 渐变孔隙率结构对恒流充电恒压放电性能的影响

多孔电极中不同孔隙结构下对应的电双层电容器的恒流充电恒压放电特性如图3 所示。如图3(a)所示，在孔隙率ε=0.67 时，电容器以100 A 恒流充电至1.8 V，然后恒压5 s，静息180 s，分别充电至最大电压为1.8、2.0、2.2 和2.4 V。每个周期的电压依次升高0.2 V，最终经过4 个周期充电电压达到2.4 V。实验中在很短时间内捕获大电流充放电是较为困难的，一般恒压充电2.2 V 放电的最大电流实际上大于2.4 V 放电时的最大放电电流。因此，通过数值模拟可以在短时间内得到准确的充放电特性。

通过采用不同孔隙结构可以提高充电电压及充放电速率。通过图3(a)和(b)的比较，可以发现采用较大孔隙率的多孔电极，电双层电容的最大充电电压有所提升。因为在较大孔隙的电极中，电解液的有效扩散系数较大，扩散阻力减小，而且迁移离子的迁移率也随之增大。从图3(a)和(c)可以看出，在多孔电极上使用渐变增加孔隙率结构可以提高最大充电电压和充放电速率。从图3(b)和(c)可以看出，对于较大孔隙的电极结构，采用渐变增加孔隙的电极结构一定程度上提高了系统的充放电速率。因此，相对于单纯的较大孔隙率而言，渐变增加孔隙的多孔结构更具有电化学优势。这是因为在渐变增加孔隙率的多孔电极中，电解质从电极内侧可以较好地扩散至电极外侧，内部电解质分布较为均匀。而且在线性增加孔隙率中，电极内侧的孔隙率较大，使得此处具有较好的扩散率及较小的扩散阻力。然而，从图3(c)和(d)中可以看出，电双层电容充放电速率有所下降，因为渐变减小孔隙率的电极内侧孔隙率较小，所以比表面积较大，从电双层中释放电解质较多，在电极内侧形成电解质的累积。此时有效扩散系数减小，扩散阻力随之增大。充放电速率有所下降。

图3 不同孔隙结构下的恒流充电-恒压放电电压电流分布

3.2 渐变孔隙率结构对不同周期恒流充电恒压放电响应的影响

电双层电容重叠的电流电压分布特性如图4 所示，从图中可以看出在恒流充电中每个周期增加的最大电压值。从图4(a)中可以看出，当孔隙率ε=0.67 时，电双层电容处于恒流100 A 充电，恒压1.4 V 放电的工况。当电压达到2.5 V 的充电上限目标电压时，一共要经历3 个周期。在2.0～2.5 V 之间的电流与电压曲线重叠，此时为电双层电容的恒功率运行状态。图4(a)与(b)相比，可以看出在较大孔隙率的电双层电容进行充电时到达各个周期的电压所需时间相对缩短，提升了充电速率。从图4(b)和(c)可以发现，采用渐变增加孔隙的电极结构，充电速率提升最为明显，缩短了充电时间。此外，从图4(d)中可以发现，对应的渐变减小孔隙结构的充放电周期加长，不利于系统性能的提升。由于渐变增加孔隙结构合理地规划了具有较大比表面积的小孔隙率电极和具有较高扩散率和迁移率的大孔隙率电极，因此，渐变增加孔隙结构更具有电化学优势，进一步提升了电双层电容器的功率密度。

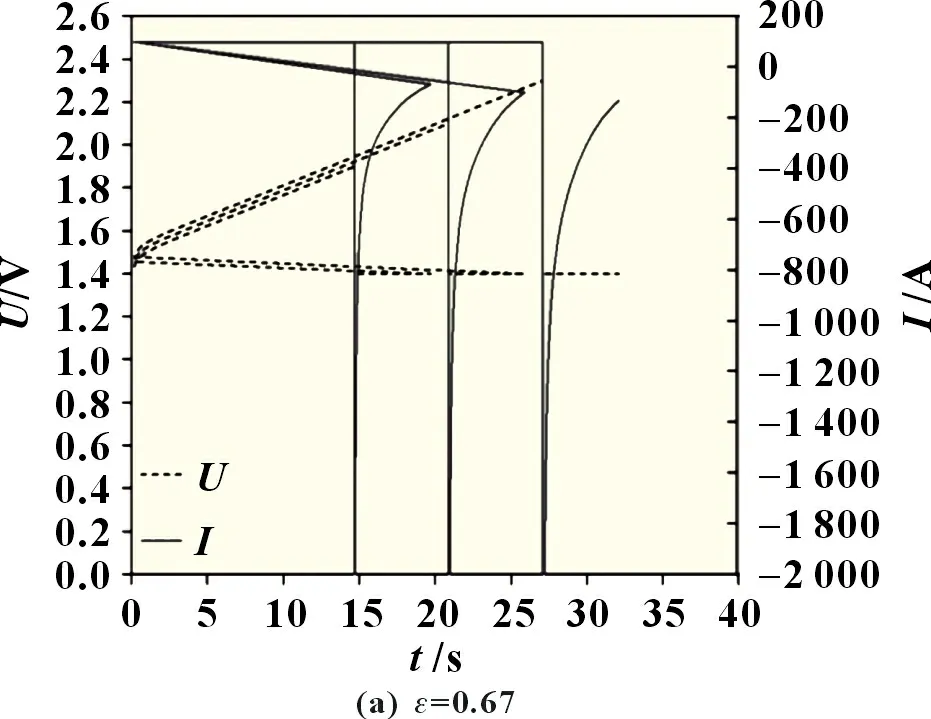
图4 不同孔隙结构下的恒流充电和恒压放电周期响应

3.3 渐变孔隙率结构对恒功率充电下电双层电流源的影响

在恒功率充电下的电双层电流源和电荷密度可以作为超级电容的电极利用率的指标。电化学电容在无量纲长度上的恒功率充电时的电双层电流源分布特性如图5 所示。从图5(a)可以看出，当孔隙率ε=0.67且系统功率为0.5 kW、静息电位为-2.1 V 时，电双层电流源差值为2.5×106A/m3；随着功率增加到0.85 kW 且静息电位为-2.5 V 时，电双层电流源差值为3.5×106A/m3。从图5(b)中可以发现，对于较大孔隙率ε=0.77 且功率为0.5 kW 时，其电双层电流源差为2.4×106A/m3；与此同时，当功率为0.85 kW 时，其电双层电流源差为3.5×106A/m3。从图5(c)中可以看出，对于渐变增加孔隙率ε=0.67～0.77 且功率为0.5 kW 时，其电双层电流源差为2.6×106A/m3；随着功率增加到0.85 kW，电双层电流源差为4.1×106A/m3。在图5(d) 中可以发现，渐变减小孔隙率ε=0.77～0.67且功率为0.5 kW，可以获得2×106A/m3的电双层电流源差；此外，功率增加到0.85 kW，与之对应的电双层电流源差为3×106A/m3。

图5 不同孔隙结构下恒功率充电下的双电层电流源

在渐变增加孔隙率中随着电极外侧孔隙率的减小，渐变电极的平均孔隙率减小，电极的比表面积增大，引起电荷在电极表面积累的空间变大，电解液中的离子聚集增多，强化了电双层电荷储存量。因此，通过改变孔隙结构可以对电双层电流源有所改进，其中渐变增加孔隙排列方式在较小功率0.5 kW 和较大功率0.85 kW，电双层电流源都有较大的提升。

3.4 渐变孔隙率结构对恒功率充电下电荷密度的影响

恒功率充电时电双层电容器的电荷密度分布如图6 所示。从图6(a)可以看出，当孔隙率ε=0.67 且功率为0.5 kW、静息电位为-2.1 V 时，电荷密度变化为4.5×106C/m3；随着功率增加到0.85 kW 且静息电位为-2.5 V 时，对应的电荷密度变化为5×106C/m3。对于较大孔隙率ε=0.77 且功率0.5 kW 时，电荷密度变化增加了5×106C/m3；随着功率增加到0.85 kW，对应的电荷密度变化增大了7×106C/m3。当渐变增加孔隙率ε=0.67～0.77 并且功率为0.5 kW，相应的电荷密度变化为4×106C/m3；随着功率增加到0.85 kW，与之对应的电荷密度变化为5×106C/m3。当渐变减小孔隙率ε=0.77～0.67 并且功率为0.5 kW，相应的电荷密度变化为4.5×106C/m3；此外，当功率增大到0.85 kW 时，其电荷密度变化为6×106C/m3。

图6 不同孔隙结构下的恒功率充电下电荷密度分布

从图6(a)和(c)中可以发现，渐变增加孔隙率ε=0.67～0.77的电极在同一低功率下的电荷密度变化比常孔隙率ε=0.67的小，随着功率的增加，在较高功率下的电荷密度与ε=0.67的变化相同。图6(b)和(c)相比可以发现，采用渐变增加孔隙率电极结构的电容器，无论是高或低功率下，电荷密度变化幅度都有所减小。一般而言，电荷分布的均匀性随充电功率的增大而减小，充电功率较低时对应的电极更均匀，电极利用率较高。渐变增加孔隙率可以在功率增大的同时保证电荷在电极上的均匀性。这是因为电极的比表面积增大，电解质溶液中的电荷更能均匀地分布在电极上。因此，与常孔隙率电极结构相比，采用渐变增加孔隙结构的多孔电极可以提高电极利用率。

3.5 渐变孔隙率结构对恒功率放电的电流电压的影响

图7 显示了不同功率参数下的放电电流和电压分布。当常孔隙率ε=0.67 且功率为0.5 kW 时，对应的电压为2.35 V；随着功率增加到0.85 kW，相应的电压为2.8 V。当常孔隙率ε=0.77 且功率为0.5 kW 时，获得的电压为2.4 V；随着功率增加至0.85 kW，与之对应的电压为2.85 V。当渐变增加孔隙率ε=0.67～0.77 且功率为0.5 kW 时，相应的电压为2.6 V；随着功率增大到0.85 kW，与其对应的电压为3.1 V。当渐变减小孔隙率ε=0.77～0.67 且功率为0.5 kW 时，对应的电压为2.3 V；随着功率增加到0.85 kW，所对应的电压为2.75 V。在常孔隙率的电双层电容中表现出充电功率越高，电压变化越大。对比多孔电极上不同孔隙结构发现，采用渐变增加孔隙率在低功率和高功率下都可以较好地提高电双层电容的放电电压。这是因为渐变增加孔隙率可以提高固相电极的有效电导率。而且与常孔隙率相比，使用这种电极结构由于电极内孔隙率的合理布置，使得电双层电容器在放电过程中的电压损失减小。

图7 不同孔隙结构下恒功率放电的电流电压分布

4 结论

本文主要研究了一种渐变孔隙分布电极结构的电双层电容器，研究结果表明，渐变增加孔隙率对其性能有较好的改进。得到的主要结论如下：

(1)在电双层电容的恒流充电恒压放电中，使用渐变增加孔隙结构相比于ε=0.67 来说，在第四个周期达到最大充电电压时，所耗费时间从680 s 缩短到620 s，减小了60 s，因此充放电速率有所提升。

(2)在不同周期恒流充电恒压放电响应中的恒功率运行下，渐变增加孔隙结构相比于ε=0.67 而言，恒功率运行状态从15～27 s 缩短到6～12.5 s，达到恒功率时所需时间缩短了15 s，一定程度上提高了系统的功率密度。

(3)针对恒功率充电下双电层电流源而言，与ε=0.67 相比，采用渐变增加孔隙率的电极结构在功率均为0.5 kW 时，电双层电流源增加了0.1×106A/m3；当功率密度均为0.85 kW时，电双层电流源增加了0.6×106A/m3。这种渐变电极结构强化了电双层电荷储存量。

(4)在恒功率充电电荷密度变化下，相对于ε=0.67 的电极结构来说，渐变增加孔隙率在功率均为0.5 kW 时，电荷密度变化减小了0.5×106C/m3；当功率增大到0.85 kW 时，电荷密度保持不变。渐变增加孔隙结构在小功率时减小了电荷密度的变化，在功率增加的同时保证了电荷在电极上的均匀性，一定程度上提高了超级电容的电极利用率。

(5)在恒功率放电下的电流电压中，相比ε=0.67 的电极结构，采用渐变增加孔隙率在功率均为0.5 kW 时，放电电压提升了0.25 V；在功率为0.85 kW 时，放电电压提升了0.3 V。这种电极结构减小了放电过程中的电压损失，适当地提高了超级电容的放电电压。