基于高斯分量标准化的K近邻故障检测策略

张 成 赵丽颖 郑百顺 戴絮年 李 元*

1(沈阳化工大学理学院 辽宁 沈阳 110142) 2(沈阳化工大学技术过程故障诊断与安全性研究中心 辽宁 沈阳 110142)

0 引 言

随着工业过程产品质量和运行安全的要求提高，工业过程的复杂性持续增加。在这种情况下，生产过程一旦发生故障，将导致生产中断等严重后果，造成巨大的经济损失。因此故障检测是生产过程中必不可少的环节。近年来，基于多元统计分析方法的复杂工业过程故障检测成为研究热点[1-3]。

主元分析PCA、动态主元分析DPCA和偏最小二乘(Partial Least Squares,PLS)等经典的多元统计分析方法在半导体、石油和化工等故障检测领域的应用中取得了丰硕的成果[4-9]。PCA通过一组线性映射将原始数据投影至低维空间，有效去除变量间的相关性，简化原始过程特性分析的复杂性[10]。DPCA引入时滞参数来构造增广矩阵，然后对增广矩阵进行PCA建模提取过程的动态信息[11]。PLS是从过程数据中提取有效的信息并建立过程模型的降维技术[12]。对于在线检测过程，PCA、DPCA和PLS方法要求运行数据近似服从单峰高斯分布。但是，在工业过程中，由于原料、产品规格、设定值和制造策略等各种因素的变化，操作条件经常会发生变化[13]。当一个进程在完全不同的运行条件下运行时，在正常运行数据中平均值和协方差的变化是显著的。在多模态过程中，数据往往不服从单峰多元高斯分布，限制了传统的多元统计方法在此类过程中的应用。Zhao等[14-15]提出了用于多模式过程监控的多模型PCA(Multiple PCA Models,MPCA)和多模型PLS(Multiple PLS Models,MPLS)。MPCA和MPLS需要过程的先验知识将运行数据按模态划分为对应于各自操作模式的数据组。此外，用户必须预定义一个相似性阈值，以合并相似的数据组。在工业实践中，上述条件对自动过程检测很难实现。

He等[16]针对多模态过程中的故障检测问题提出了一种K近邻KNN故障检测方法。KNN通过比较测试样本与近邻训练样本的距离和正常样本与近邻训练样本的距离来检测故障[17]。与传统的多元统计方法相比，KNN方法具有更好的故障检测性能，并且成功应用于半导体制造中的故障检测。然而，KNN方法也具有一定的局限性。KNN是基于距离的故障检测方法，而实际工业过程中数据的均值和方差会随着操作条件的切换而发生变化，使得正常数据的统计距离异常扩大，导致故障样本未被有效识别。然而由于KNN处理高维数据时，计算量较大，因此He等[18]提出了一种基于主成分的KNN(Principal Component based KNN,PC-KNN)故障检测方法减少KNN的计算量。但该方法应用于主成分空间进行故障检测，忽略了残差子空间中的故障。针对PC-KNN的缺陷，郭小萍等[19]提出了一种基于特征空间的KNN故障检测方法，改进了故障检测性能。为了避免KNN方法受到参数K值的选取的影响，Song等[20]提出局部信息KNN(Locally Informative KNN,LI-KNN)和全局信息KNN(Globally Informative KNN,GI-KNN)方法。冯立伟等[21]提出了基于权重K近邻(Weighted KNN,WKNN)的多模态故障检测方法。WKNN通过引入近邻距离的权重，保持数据离散程度的一致性。但是在实际工业过程中，WKNN在搜索近邻时必须遍历所有样本，导致计算成本高昂。

监控多模态过程的主要挑战是如何确定历史数据中的模式数和在线样本的操作模式。因此高斯混合模型GMM被提出用于解决此问题[22]。GMM是一种无监督学习算法，采用混合高斯概率密度函数来模拟多变量数据集的统计分布，并已成功地应用到多个领域中[23-24]。Choi等[25]将GMM与PCA和DA集成，用于检测和隔离非线性、多状态或动态过程中的故障。PCA-GMM将每个监控样本确定地归类到一个特定的高斯聚类中，然后选择相应的局部PCA模型进行故障检测。Yoo等[26]将类似的策略与多路主成分分析相结合，用于监控生物批处理过程。

针对复杂多工况过程故障检测问题，本文提出一种基于高斯分量标准化的K近邻GCS-KNN故障检测策略。首先对数据进行预处理，运用GMM将预处理后的数据分解为多个高斯分量，计算每个高斯分量的均值和协方差；然后应用每个高斯分量的统计信息对样本进行标准化；最后利用KNN方法对过程进行检测。GCS-KNN不仅能够消除数据的多模态特征，并且可以减少建立模型的个数，极大地降低了检测过程的复杂度。通过数值例子和半导体蚀刻过程仿真实例，进一步证实本文方法相比于其他方法具有明显的优势。

1 基本算法

1.1 高斯混合模型GMM

假设X∈RN×m，N为样本数，m为维度。其中X={x1，x2，…，xN}每个样本x的概率密度函数表示为：

(1)

式中：k为GMM中高斯分量的个数；ωi为第i个高斯分量的权重。

θi={μi，Σi}

(2)

Θ={θ1，…，θk}={μ1，Σ1，…，μk，Σk}

(3)

式(2)和式(3)分别代表局部和全局高斯模型的参数(μi为均值向量，Σi为协方差矩阵)，第i个高斯分量的高斯密度函数表示为：

(4)

采用极大似然估计(Maximum Likelihood Estimation,MLE)方法求解Θ={{ω1，μ1，Σ1},…,{ωk，μk，Σk}}参数，数据集X的对数似然函数如下：

(5)

参数估计问题进一步表示为：

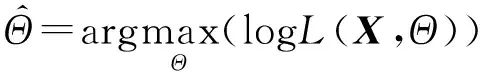
(6)

MLE方法通过令对数似然函数的一阶导数为零来分析估计参数Θ。但是由于解析解可能导致高斯模型参数的奇异或病态估计，因此，使用EM算法来估计最大似然分布参数。通过重复期望步骤(E-step)和最大化步骤(M-step)来迭代计算后验概率。然后计算相应的分布参数，直到满足对数似然函数的收敛准则。

(1) E-步骤：

(7)

式中：p(s)(ck|xj)表示经过s次迭代后第j个训练样本属于第k个高斯分量的后验概率。

(2) M-步骤：

(8)

(9)

(10)

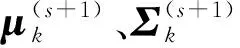
1.2 K近邻规则故障检测

KNN方法主要通过判断测试样本到其K近邻的距离与正常样本到其K近邻的距离大小来检测样本状态。在训练样本中找到每个样本的K个近邻，并计算样本与其K个近邻的欧氏距离平方和，如下：

(11)

(12)

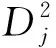
2 策略设计

在多模态过程故障检测中，常用的KNN方法由于其模型简单，并且具有无须估计参数、精度高对异常值不敏感等特点，使其具有较好的检测结果。但是KNN也具有一定的局限性，当样本分布不均衡且模态间方差差异较大时，KNN会根据较大的统计量确定控制限，若产生微小故障，会造成漏报的后果。为了避免这一现象，本文提出了基于高斯分量标准化的K近邻故障检测策略。

假设X∈RN×m为来自多工况过程的数据，N为样本数，m为维度。利用GMM建立高斯混合模型，通过式(7)-式(10)计算出每个高斯分量的统计信息。根据式(13)计算样本属于第k个高斯分量的后验概率。

(13)

将样本X分解为多个高斯分量子集{Y1,Y2,…,Yk}，其中Y1表示第一个高斯分量的样本集，Y1={y1,y2,…,yk}。通过GMM将训练数据分解为多个高斯分量，并对每个样本应用高斯分量的统计信息进行标准化处理：

(14)

式中：yi、μi和Σi分别为第i个高斯分量的样本、均值和协方差。应用式(14)对每个高斯分量进行标准化处理，原本稀疏模态的数据由发散向中心聚拢，密集模态的数据由中心向外扩散。也就是说，正常数据从多峰结构转换为遵循单峰多元高斯分布的结构，从而消除了多峰特性的影响。最后应用KNN方法对过程进行检测。将GMM与高斯分量标准化方法相结合，不仅降低了模型的复杂度，简化计算量，而且有效地提高了检测率。GCS-KNN的检测过程由离线建模和在线检测两部分组成，其检测流程如图1所示。

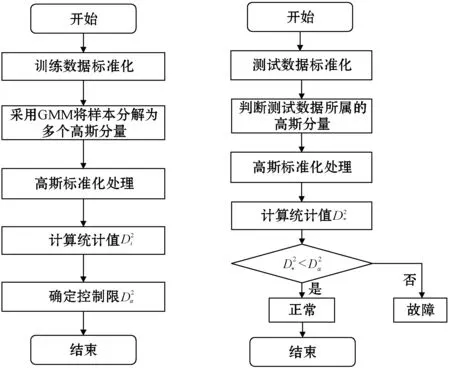
图1 GCS-KNN故障检测流程

2.1 离线建模

(1) 首先对训练样本中的数据采用z-score方法进行预处理。

x*=(x-μ)σ-1

(15)

式中：μ为训练样本的均值；σ为训练样本的标准差对角矩阵。

(2) 将标准化后的样本应用GMM分解为多个高斯分量，通过式(7)-式(10)得到每个高斯分量的参数μk、Σk和ωk。

(3) 通过式(14)对分量进行高斯分量标准化处理，消除多模态特征。

2.2 在线检测

(1) 测试样本采用式(15)中的μ和σ进行预处理。

(2) 应用式(13)计算测试样本x*属于第k个高斯分量的后验概率，判断其所属的高斯分量。

(3) 利用式(14)对每个样本进行高斯分量标准化处理。

3 数值例子

本节通过改进文献[27]中的一个数值例子对本文方法进行验证，具体模型如下：

Xj=Ξjsj+ejj=1,2,3

(16)

式中：sj=[s1,j，s2,j]T是高斯随机向量，ej服从均值为零和标准差为0.05的正态分布，变换矩阵为Ξj∈R3×2。

(17)

每个模态根据式(16)和式(17)产生300个样本，共产生900个样本作为正常的训练数据，同时每个模态各产生50个样本作为校验样本。另外，在第一个模态上添加了阶跃故障生成100个故障样本。表1列出各模态产生训练数据集的参数。数据分布如图2所示，为了清晰展示数据结构，将故障样本所属的模态数据放大。

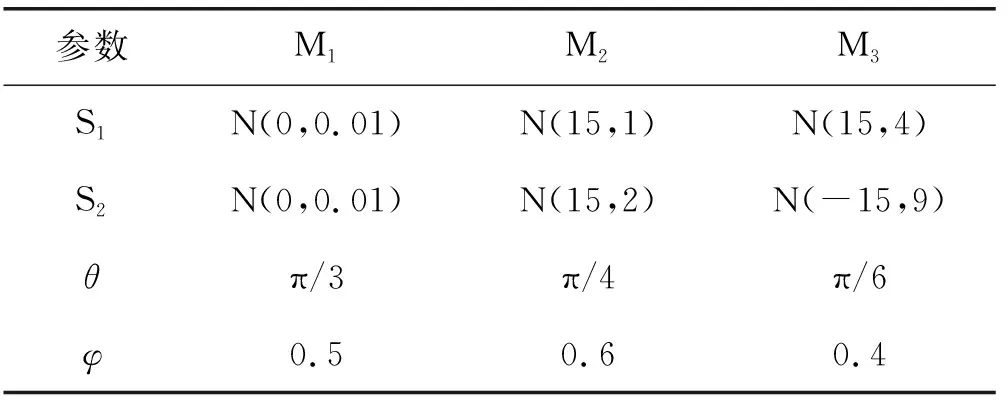
表1 各模态参数设置

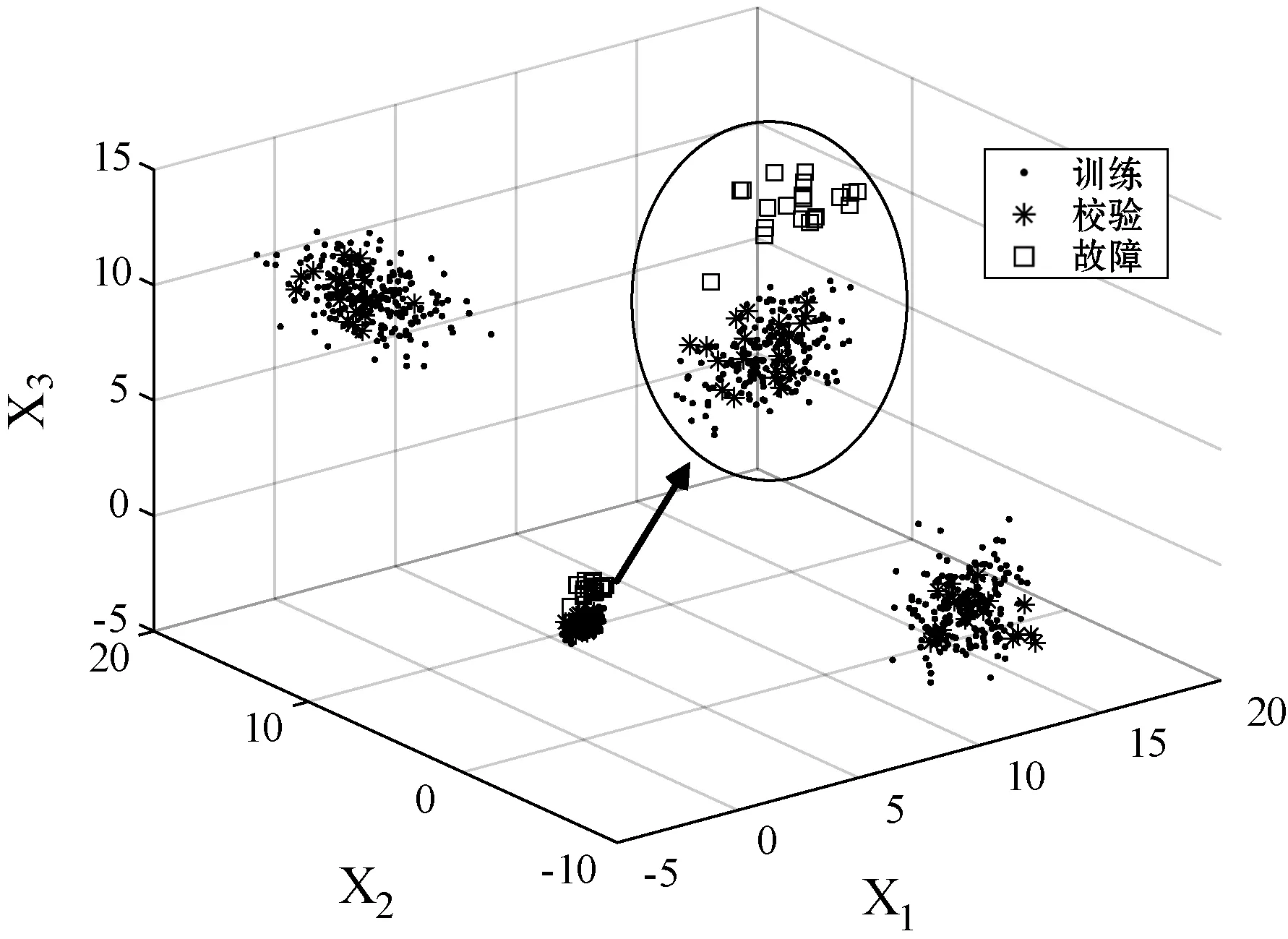
图2 数据散点图

由图2可知，数据呈现多模态结构且各模态方差差异明显。本节分别使用PCA、DPCA、KNN、WKNN和GCS-KNN对该数值例子进行检测。根据主元贡献率达到85%，PCA主元个数选取为2[28]。DPCA的时滞参数和主元个数确定为2，WKNN的权重参数k选取为3，WKNN、KNN和GCS-KNN近邻数K均确定为5，具体参数设置如表2所示。各方法的置信度为99%。首先应用PCA和DPCA检测此数据集，在置信度为99%的情况下，其检测结果如图3、图4所示。由于PCA和DPCA均使用统计量T2作为检测指标，而此数据集具有显著的多峰分布特征，不满足统计量的假定前提要求，故导致出现漏报的情况，检测效果较差。

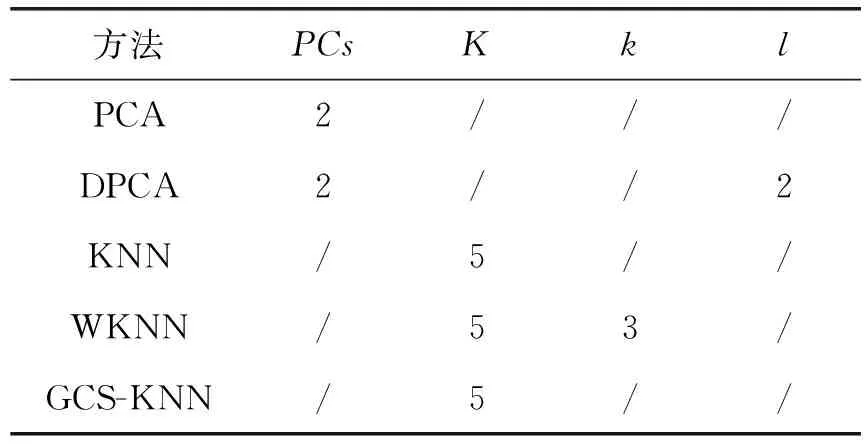
表2 各方法参数设置

图3 PCA检测结果

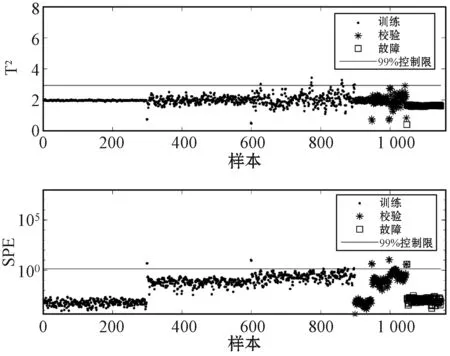
图4 DPCA检测结果

KNN方法通常用于有多模态特征的数据，但是，当多个模态的方差差异较大时，控制限则根据较大的统计值确定。若在方差较小的模态附近产生微小故障时，会出现漏报的现象。本例为方差差异较大的多模态数据，此时，KNN统计信息无法反映故障数据与正常数据之间的差异。由于KNN由方差较大的模态数据确定控制限，而此数据集的故障发生在较小方差模态的附近，所以KNN检测方法针对此数据集的检测效果较差，如图5所示。WKNN通过引入距离权重，消除KNN无法检测出多模态过程中微小故障的局限性，故能够检测出大部分故障，其检测结果如图6所示。但是WKNN在对数据量大的过程进行故障检测时，存在计算量大、及时性差等问题，并且模型的性能易受到参数的影响，因此在故障检测时存在局限性。

图5 KNN检测结果

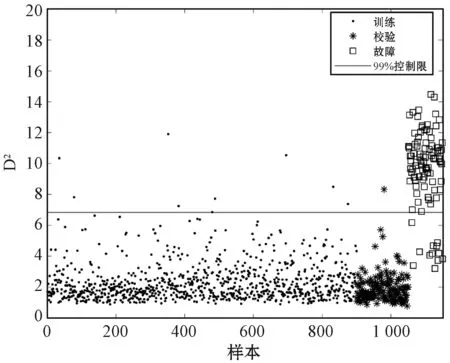
图6 WKNN检测结果

GMM对样本的分类结果如图7所示，将训练数据分解为3个高斯分量。图8为各个高斯分量标准化后的数据散点图，高斯分量标准化可将故障数据和正常样本分离，消除了多峰特征的影响，数据遵循多元高斯分布，符合统计量的假设前提条件，为后续的检测过程提供了较好的数据基础。经过标准化后的样本采用KNN进行故障检测，样本中的所有故障都能够被检测出来，如图9所示。该数值例子表明本文方法能够通过高斯分量标准化消除数据的多模态特征，因此可以有效地检测多模态过程。

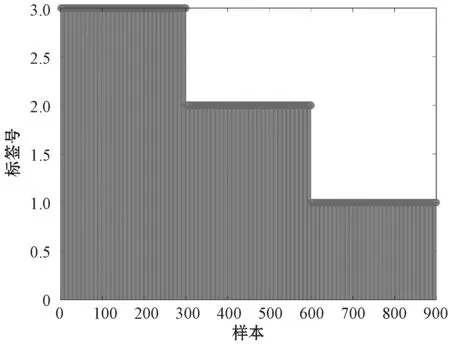
图7 数据分类图

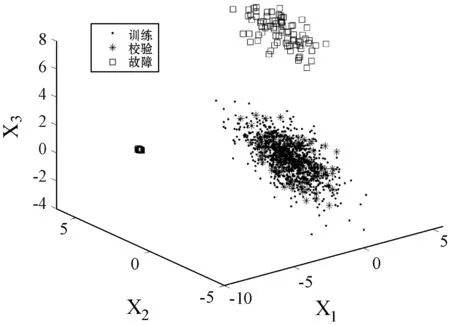
图8 标准化后的数据图

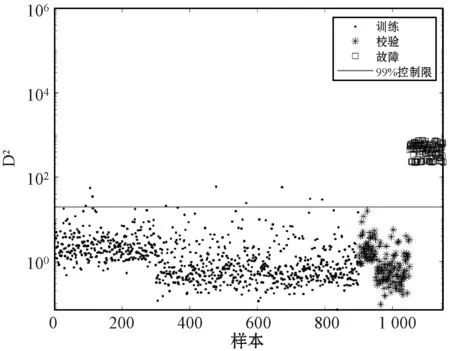
图9 GCS-KNN检测结果

4 半导体工业例子

本节以半导体蚀刻工艺为例，验证GCS-KNN的有效性[29]。该数据包含108个正常晶片和21个故障晶片。由于两片晶片丢失大量数据信息，故本节实验仅使用107片正常晶片和20片故障晶片用于测试。在本次仿真实验中，选取96批正常数据作为训练数据建立模型，11批校验数据，20批故障数据用于测试模型。半导体工艺具有间歇时间不等、步长不等、过程漂移以及多模态等特点。为了提高不等长批处理过程的故障检测性能和降低算法的复杂度，利用统计模量分析(Statistical Pattern Analysis,SPA)对半导体数据进行展开[30]。

本节分别采用PCA、DPCA、KNN、WKNN和GCS-KNN对半导体数据进行故障检测并进行对比分析。本节中各参数设置如下，其中PCA主元个数选取为3，DPCA主元数和时滞参数分别选取为13和2，根据交叉验证，KNN和GCS-KNN的近邻数为9，WKNN的参数K和k设置为9。各方法置信度为99%。

图10和图11分别为PCA和DPCA方法用于该例的检测结果，可知PCA和DPCA用于该例的检测率较低。其主要原因是半导体过程的数据是由相隔数周的多次实验中收集的，受到不同批次生产工具状态变化的影响，导致不同批次数据间存在不同的均值和协方差信息。此外，由图12可以发现降维后的主元空间仍然具有多模态结构，影响PCA与DPCA检测模型的检测性能。图13为使用KNN对该例进行故障检测的结果，KNN算法对多模态数据具有较好的检测效果，但是前提是多模态数据为模态方差差异不明显的数据。否则其控制限会由较大的统计值决定，导致出现漏报的情况，因此KNN方法的检测率也较低。WKNN的检测结果如图14所示，WKNN通过引入权重将每个模态的稀疏程度调整为相同的尺度，消除了模态间不同离散程度对故障检测的影响。但是，WKNN的计算量很大，原因是在搜索近邻时必须遍历所有样本。

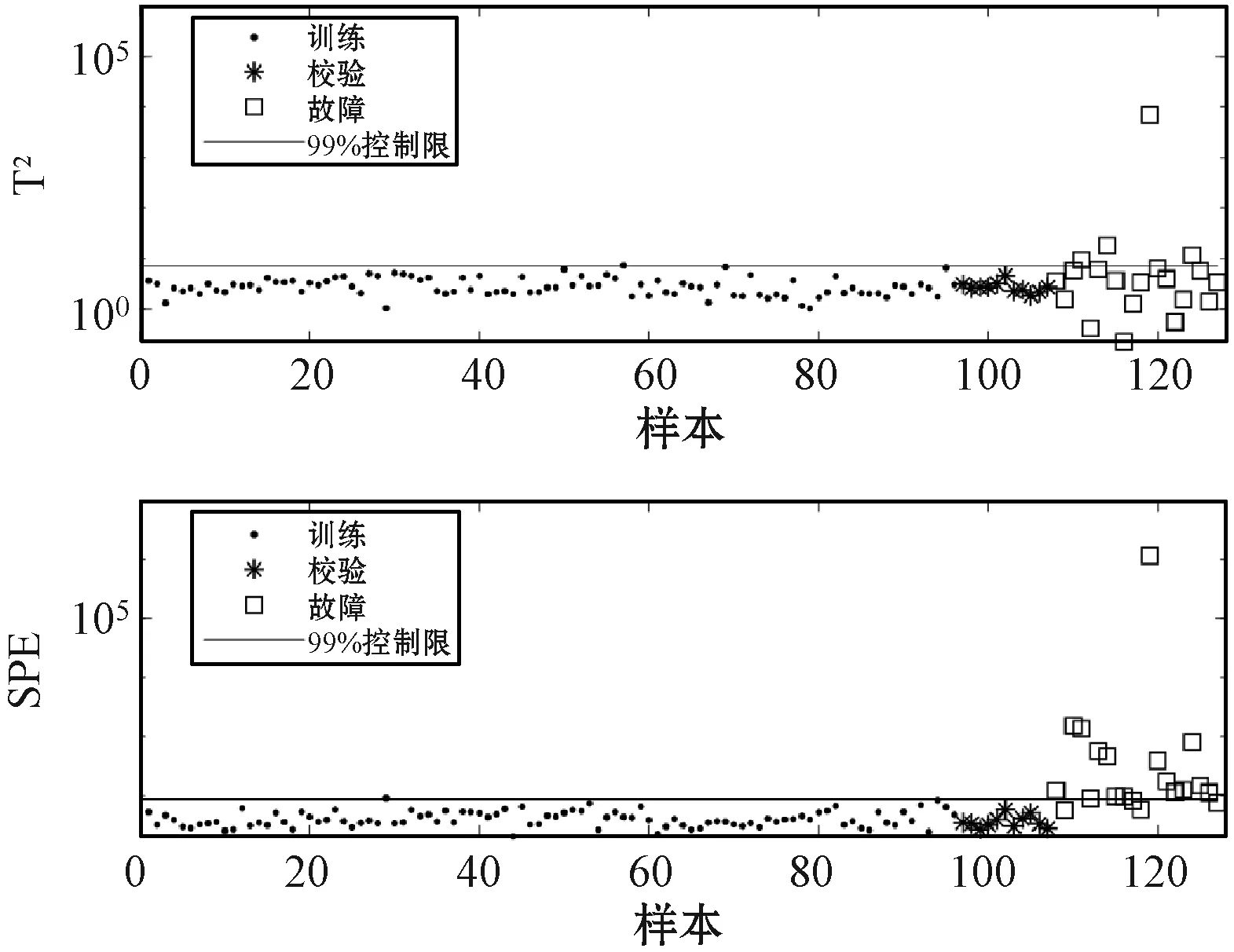
图10 PCA检测结果

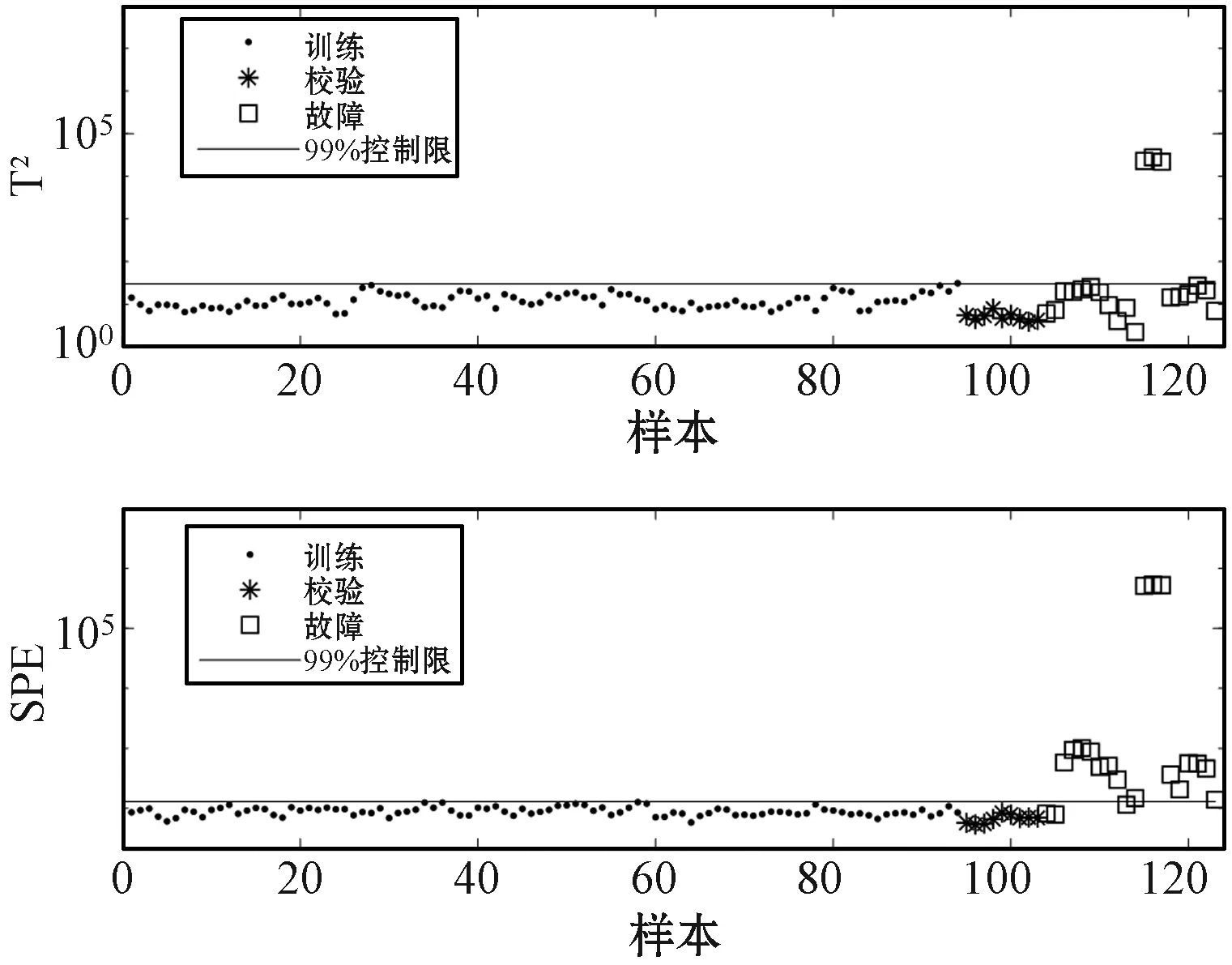
图11 DPCA检测图

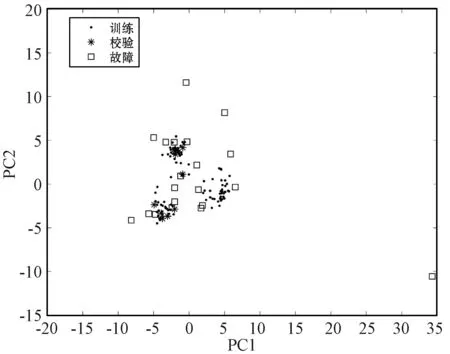
图12 主元空间散点图

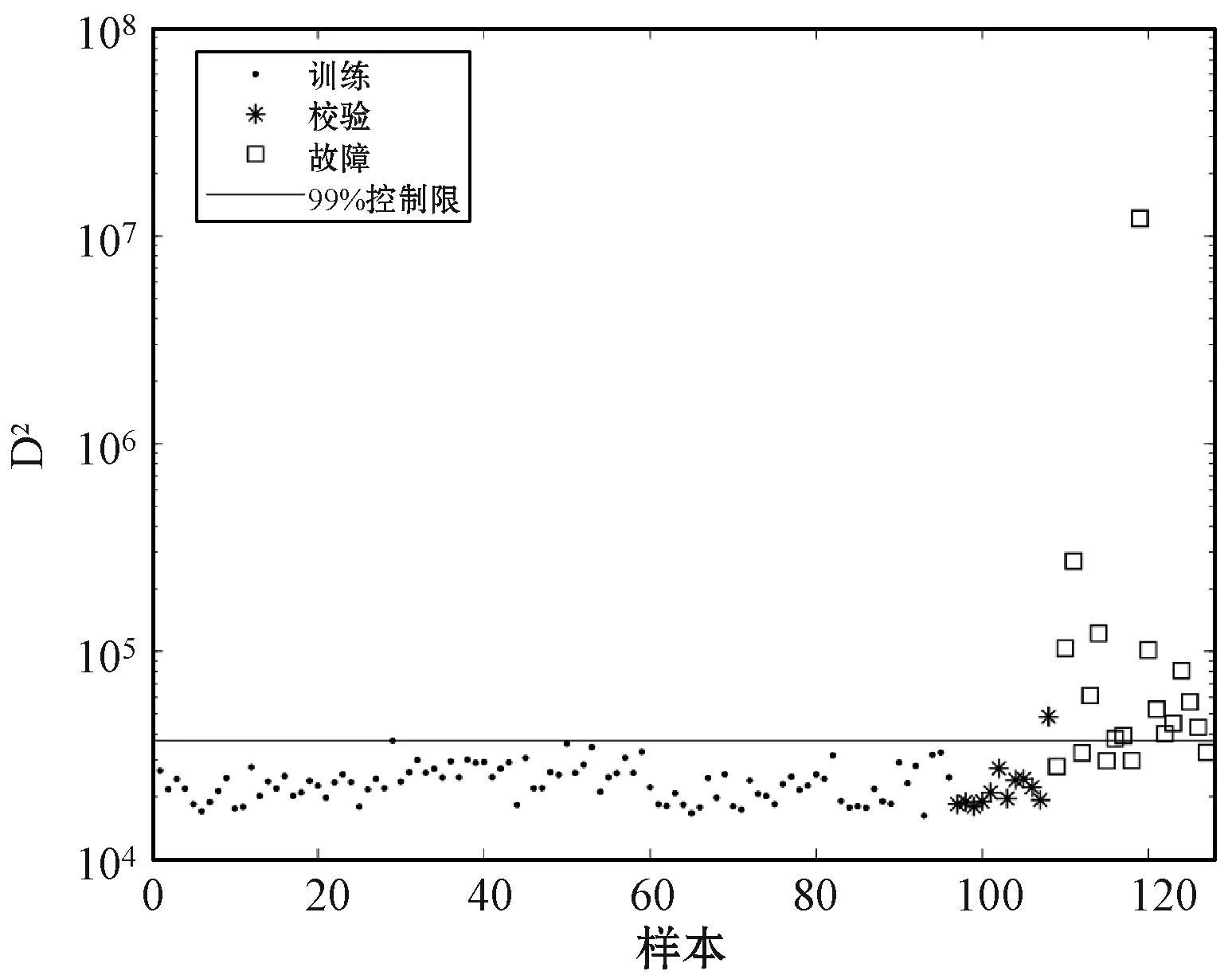
图13 KNN检测结果

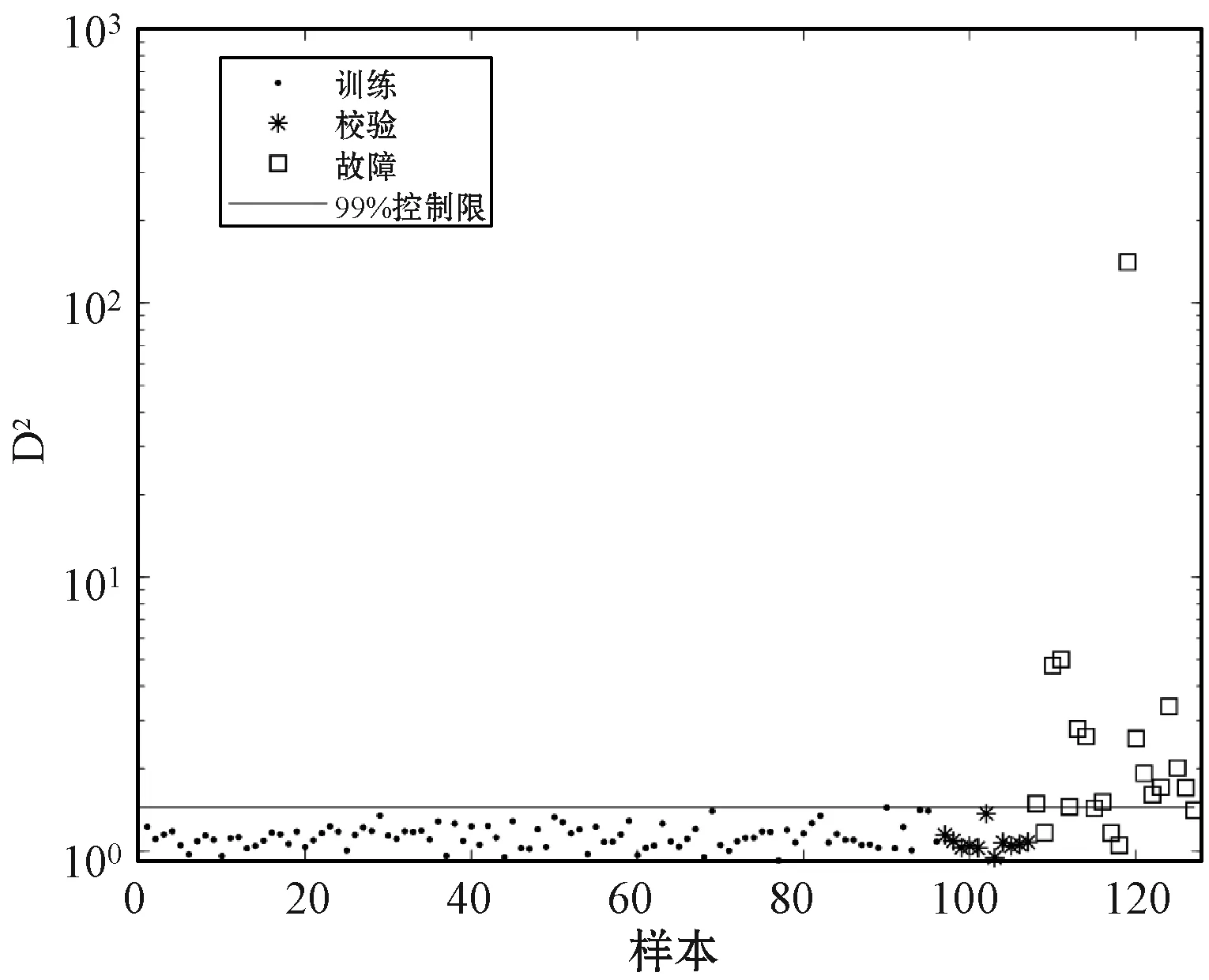
图14 WKNN检测结果

图15为半导体数据经过高斯分量标准化处理的数据图，由图知高斯分量标准化有效地消除了数据的多模态特征。同时，由图16可以发现，大部分故障能够和正常数据分离，为后续的检测过程带来了良好的数据基础。标准化后的数据应用KNN进行故障检测，大部分故障均能够被检测，GCS-KNN的检测率达到0.95。由表3可知GCS-KNN故障检测率明显高于其他方法。综上，实验结果验证了本文方法的有效性。

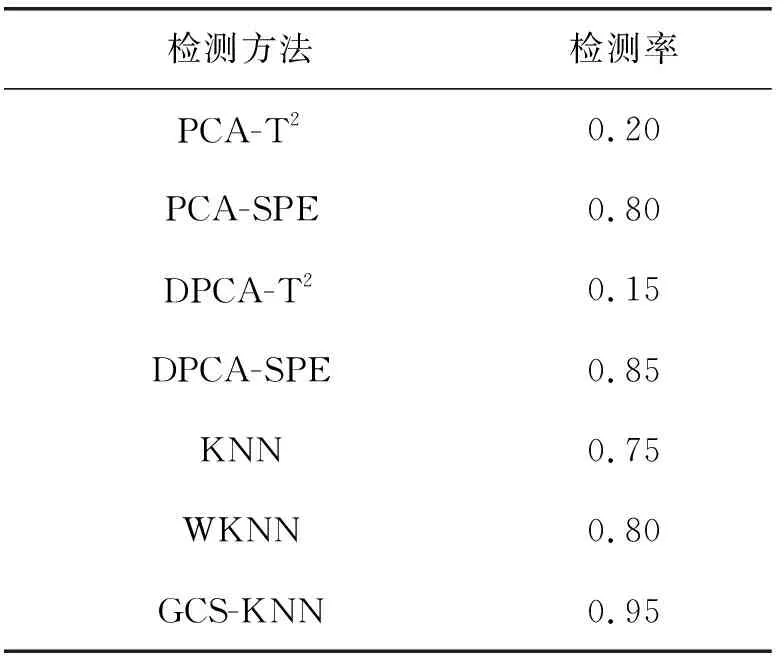
表3 各方法故障检测率

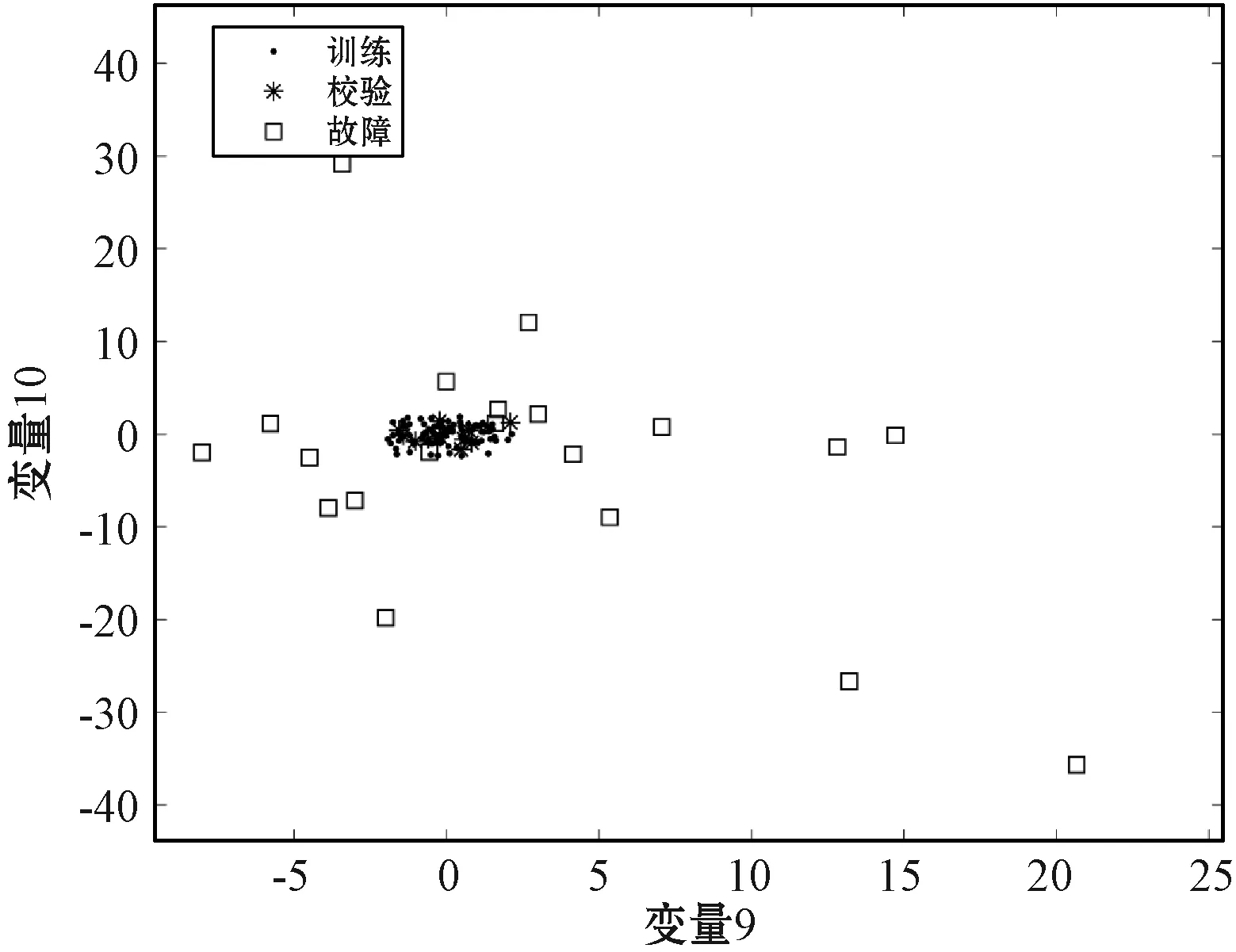
图15 GCS标准化的数据图

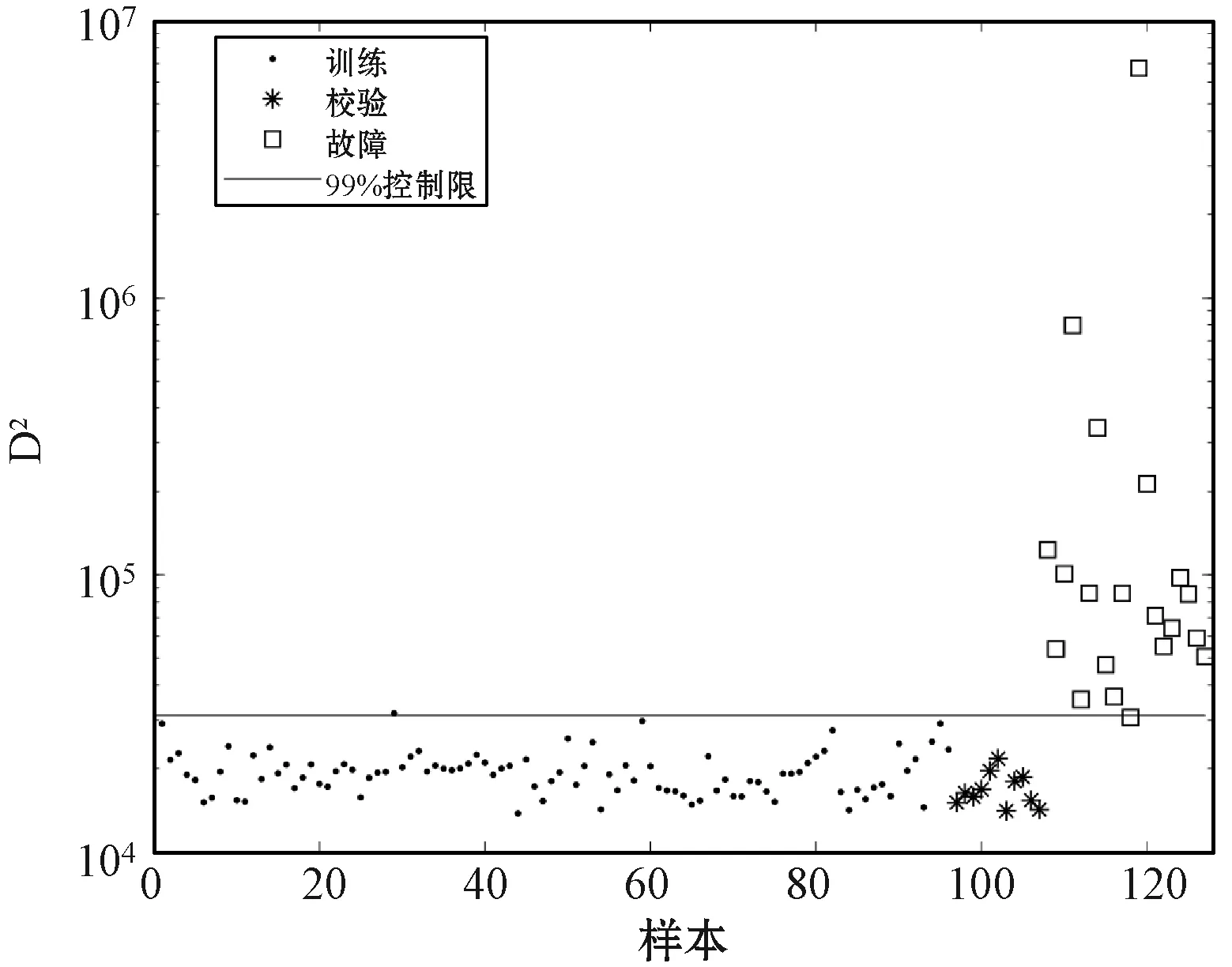
图16 GCS-KNN检测结果

5 结 语

本文提出一种高斯分量标准化的方法消除数据的多模态特征，在此基础上,结合高斯分量标准化与KNN，提出了一种多模态过程检测方法。首先，该方法利用高斯分量标准化描述多模态过程，从而提高了基于KNN方法在复杂过程中的检测性能；其次，GMM将过程数据分解为多个高斯分量，且各分量中的数据服从多元高斯分布，为后续的检测过程提供了较好的数据基础。由数值例子和半导体蚀刻过程的仿真实验验证该方法的有效性。仿真结果表明高斯分量标准化能够有效将多模态数据转化为单一分布的数据，提高KNN在多模态工业过程中的检测效果。然而GCS-KNN在已知过程数据模态个数先验知识的前提下具有良好的检测效果，因此如何获取过程数据模态个数成为下一步的研究方向。