空塔横风向振动分析讨论

赵 耿，赵云浩

（江苏金诺化工装备有限公司，江苏 宿迁 223800）

塔式容器在化工、石化、医药、石油天然气及轻纺等行业应用广泛。塔式容器结构方面的突出特点是高径比大，设计时要考虑风载荷诱发的塔体振动[1]。风载荷分为横风载荷和顺风载荷，其中横风载荷对塔式容器的影响和危害较大。低风速下的横风载荷振动振幅过大时，甚至会危及塔式容器的安全使用。近年来塔式容器工业应用朝着大型化发展，风载荷诱发振动的频率也在增加[2]，处于内部填料、塔板等内件和外部平台管线尚未安装阶段的裸塔，更容易发生诱导振动。

国内塔式容器设计主要依据是NB/T 47041—2014《塔式容器》[3]。NB/T 47041—2014 规定，当塔式容器的高径比H/D＞15且高度H＞30 m时，还应计算横风向风振。NB/T 47041—2014中提供了判别共振的方法和发生横风向振动时塔顶振幅的计算方法。在塔顶振幅计算的基础上，依次计算共振时组合风弯矩和塔器的轴向应力可以进行塔式容器的安全性判定。但NB/T 47041—2014中未规定塔式容器振幅的许用值，现场安装条款表述也很笼统，只是提出必要时应根据需要设置螺旋形扰流片。塔式容器因而缺少振幅设计校核的具体依据。此外，常用设计软件如SW6在风诱导共振核算方面程序设计不足[4]，许多设计者回避甚至忽略了该问题，导致了某些塔式容器工程项目中的设计计算结果合格，设备实际安装甚至操作时却产生剧烈振动、振幅远大于计算值的后果。

2021-08，某院设计的1台乙二醇浓缩塔在宁夏一工业园区安装期间发生了明显振动，文中以此塔式容器为例，结合NB/T 47041—2014与压力容器设计标准分析探讨高耸塔式容器的横风向振动设计考虑要点要素，补充和完善标准方法的不足。

1 塔式容器横风向振动案例分析

1.1 振动类型判定

1.1.1 塔式容器概况

某乙二醇浓缩塔式容器设计参数为，压力0.3/-0.1 MPa，设计温度200℃，内部介质为乙醇、丁醇、草酸二甲酯、水等，高度49 275 mm，内径1 800 mm，材质 S30408+Q345R，腐蚀裕量 0 mm，厚度3+16/3+12/12 mm，内部填料高度6 800 mm（4段）+3 200 mm（1 段），基本风压 450 Pa，地面粗糙度B，设备质量（不含填料）42 160 kg。其结构尺寸见图1。

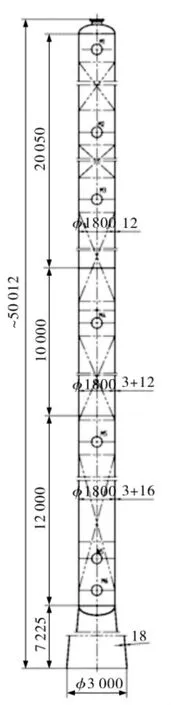
图1 某乙二醇浓缩塔式容器结构尺寸示图

1.1.2 临界速度判定法

根据施工期间现场的视频和图片分析，该塔的实际振动周期约1.1 s，振幅约0.3～0.4 m。该填料塔在现场安装时无内部填料，依照NB/T 47041—2014进行空塔状态下的振动校核计算，得到第一振型自振周期T1=1.22 s，第二振型自振周期T2=0.22 s。第一振型临界风速vc1=7.45 m/s，第二振型临界风速vc2=41.3 m/s，设计风速v=34.7 m/s。

若是改用SW6软件进行计算，按照此塔式容器材料为复合板输入的壁厚一般是基层厚度，则会出现因设备设计厚度及质量相对实际值偏小，计算出的自振周期相应偏大的情况。这对后续振幅、强度等计算结果的影响偏保守，在工程上是可以接受的。

按照NB/T 47041—2014中的方法，通过比较v与vc1分情况判别共振，①若v＜vc1，不需考虑塔式容器的共振。②若vc1≤v＜vc2，应考虑塔式容器的第一振型的振动。③若v≥vc2，除考虑塔式容器的第一振型外还应考虑第二振型的振动。

现在该设备v=34.7 m/s，此值大于vc1而小于vc2，会产生第一振型的振动。振动期间当地的风力为 4～5级，10 m高度的风速 v10为 5.5～10.7 m/s，塔顶的风速为：

风压高度变化系数fi按标准取值1.662，可以得到vH在7.1～13.8 m/s。对于圆截面结构，风速约为1～1.3倍的vc1，处于共振状态的锁定区域[2]。所以结合塔器的振动情况，可以判断该振动为横风向振动,并且只发生1阶振动。

1.1.3 其他判定法

除了临界速度的判定，还有其他的判定方法及准则，文献[4]中有详细介绍和比较。现主要对国内相关标准使用的准则进行说明。

横风向风振机理复杂、影响因素多，工程结构中易于遇到且机理相对清楚的振动形式包括涡激振动、驰振、颤振及抖振等[5]。其中，最为常见的是涡激振动，又称卡门涡街[2]，其振动机理表述为，当风以一定的速度绕流圆柱形塔时，会在柱体背后的两侧形成周期性交替漩涡并以一定频率从柱体表面上脱落，在尾流中有规律地交错排列成两行。在漩涡形成和脱落过程中，塔体两侧气压会产生相同周期变化，从而在侧面产生周期变化的升力，引起塔振动。雷诺数大小决定着漩涡形成的规律性和频率。

GB/T 50009 —2012 《建筑结构载荷规范》[6]基于雷诺数大小，将风振划分为亚临界、超临界、跨临界3种，并规定当亚临界和跨临界风振时进行横风向核算，当超临界风振时可以不考虑。但实际工程经验是，符合超临界范围的风振会导致建筑物剧烈振动，本文讨论的塔式容器便是发生了该范围内的风动。可见，雷诺数对气动阻尼参数影响较大，更能反映振动效应[7]，影响升力系数，作为判定准则则存在一定不足。

GB/T 50051—2021《烟囱工程技术标准》[8]中不再以雷诺数作为判定钢制烟囱共振条件，而是改用临界风速判定依据。GB/T 50051—2021对振动强度进行判定，使用烟囱的单位质量和阻尼计算斯科顿数Sc，依据Sc值判断是否采取相应的措施避免烟囱变形过大破坏或疲劳破坏。GB/T 50051—2021规定，①当Sc≤5时，应安装减振装置。②当5＜Sc≤15时，可安装减振装置，或进行抗疲劳设计。③当Sc＞15时，可不安装减振装置。空塔设计可以参考这种判定准则。

Sc计算如下：

其中

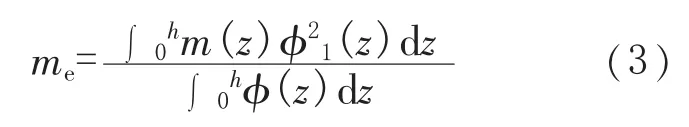
式中，ρa为空气质量密度， 取值 1.25 kg/m3；d1为烟囱顶部1/3高度范围筒身平均外直径，m；ξs为烟囱结构阻尼比，标准中规定为0.01；me为当量单位高度质量，m(z)为单位高度质量，kg/m；ϕ1(z)为第一阶振型。

1.2 共振振幅分析

1.2.1 问题

依据NB/T 47041—2014，振幅按下式计算。

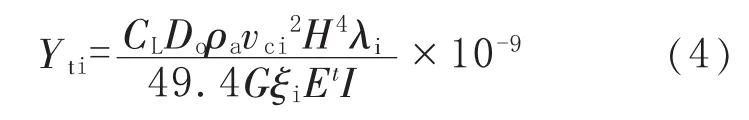
式中，CL为升力系数，与雷诺数相关；Do为设备外径，H为容器高度，mm；υci为共振时临界风速，m/s；λi为计算系数，按 NB/T 47041—2014选取；G为系数，按NB/T 47041—2014选取；ξi为阻尼比；Et为设备的弹性模量，MPa；I为设备截面惯性矩，mm4。

从式（4）可以看出，振幅的影响因素有很多，但在设备外形尺寸、设备质量、材料、外界环境相同的情况下，影响振幅计算结果的因素就明确为阻尼比。对现场发生共振晃动的乙二醇浓缩塔应用式（4）计算振幅。NB/T 47041—2014中规定的阻尼比在0.01～0.03，校核计算时选取的值为0.01。因振幅与阻尼比成反比，而实际的振幅又大，可定性判断出相应空塔状态下的阻尼比会标准最小值还要小。

1.2.2 讨论

阻尼比是线性黏性阻尼系数和临界阻尼的比值，其大小与塔器材料、结构尺寸、内部填料或塔盘、振型等因素有关，受塔式容器的种类、尺寸、结构的多样性及其越来越复杂的发展趋势限制，阻尼比还没有标准化的统一计算公式，目前主要是通过实验得到。

文献[9]中通过实验模拟特定结构塔的振动得出结论，该塔在无塔盘和有塔盘时的一阶固有频率一致，即振动周期相同，并且塔盘内的液体可以增大塔体的阻尼比。于此可以看出，一定小间距均布的塔盘有增大阻尼比的作用，操作工况的物料也有增大阻尼比的作用。填料塔中填料也是有效的阻尼物，在振动时，填料内部的流体也会随之晃动改变分布[10]，这也会增加阻尼比。

塔式容器操作工况阻尼比通常不会小于NB/T 47041—2014中的阻尼比推荐值，但某些大高径比的高耸塔式容器会有例外，其实际振幅相应超出计算振幅。塔式容器结构种类繁多，其操作工况下的阻尼比无法具体计算，多通过实验得出。本文仅计算空塔下的阻尼比。

SH/T 3098—2011《石油化工塔器设计规范》[11]附录F中建议，在进行风力和风弯矩校核计算后，再增加裸塔（即无保温、无平台梯子、无管道连接、无介质的塔器）的横风向共振计算校核，且此时一阶振型的阻尼比取值不应高于正常操作工况时的阻尼比。SH/T 3098—2011未进一步给出空塔阻尼比具体计算公式。

ASME STS-1—2017《Steel Stacks》[12]中 将烟囱阻尼比定义为结构阻尼比+气动阻尼比。其中，结构阻尼比与烟囱支承形式和内部是否有衬里有关，不带衬里的刚性支承烟囱的结构阻尼比ξs为0.002,气动阻尼比ξa用下式计算。

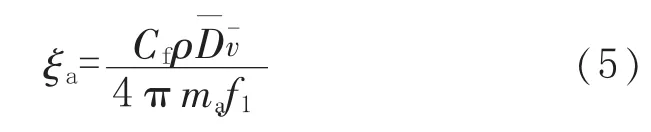
式中，Cf为升力系数，按 ASME STS-1—2017选取；ρ为空气密度，kg/m3；为烟囱顶部 1/3高度范围筒身平均外直径，m；v为平均风速，m/s，此处可以取一阶临界风速；ma为距离烟囱顶1/3处的单位长度质量，kg/m，可以按式（3）计算；f1为烟囱的一阶振动频率，Hz。空塔构造与烟囱相似，确定空塔横风向振幅时，可以参考式（5）计算阻尼比，然后将阻尼比计算值代入式 （4）中计算振幅，得到的振幅计算结果可作为判断塔式容器振动情况的考量项。

2 塔式容器横风向振动案例有限元分析

2.1 振动特性模态

常规计算中，不同厚度的塔式容器的计算模型为多自由度体系，求解方法是利用折算质量法求其近似解。该方法只能求出基本振型的自振周期，高振型的自振周期还要采用其他的计算方法。为了更准确地计算自振周期，下面进行有限元分析，对乙二醇浓缩塔进行振动特性模态分析，求解前三阶的振动周期。

简化模型，仅对筒体进行建模，略去接管、法兰等部件，将质量集中到壳体上。根据筒体复合板厚度和式（6），计算当量弹性模量 Et，弹性模量取30℃时数据。分别在空塔和操作（不考虑内部压力）两种情况下进行模态分析。因填料的弹性模量相对较小，在操作工况将填料的质量当量到壳体上，填料的含液密度为210.7 kg/m3。分段计算Et，计算过程中需要的第一段～第四段筒体的弹性模量依次为2.005×1011MPa、1.996×1011MPa、1.993×1011MPa、1.943×1011MPa，第一段～第四段筒体的密度见表1。

表1 筒体复合板厚度计算用分段密度 kg/m3

式中，E1为基层材料弹性模量，E2为复层材料弹性模量，MPa；δ1为基层材料的有效厚度，δ2为复层材料的有效厚度，mm。

使用壳单元shell63建模，然后进行模型的振动模态分析，得到的前3阶空塔状态下多阶振动特性见图2。根据图2中振动频率计算的振动周期见表2。

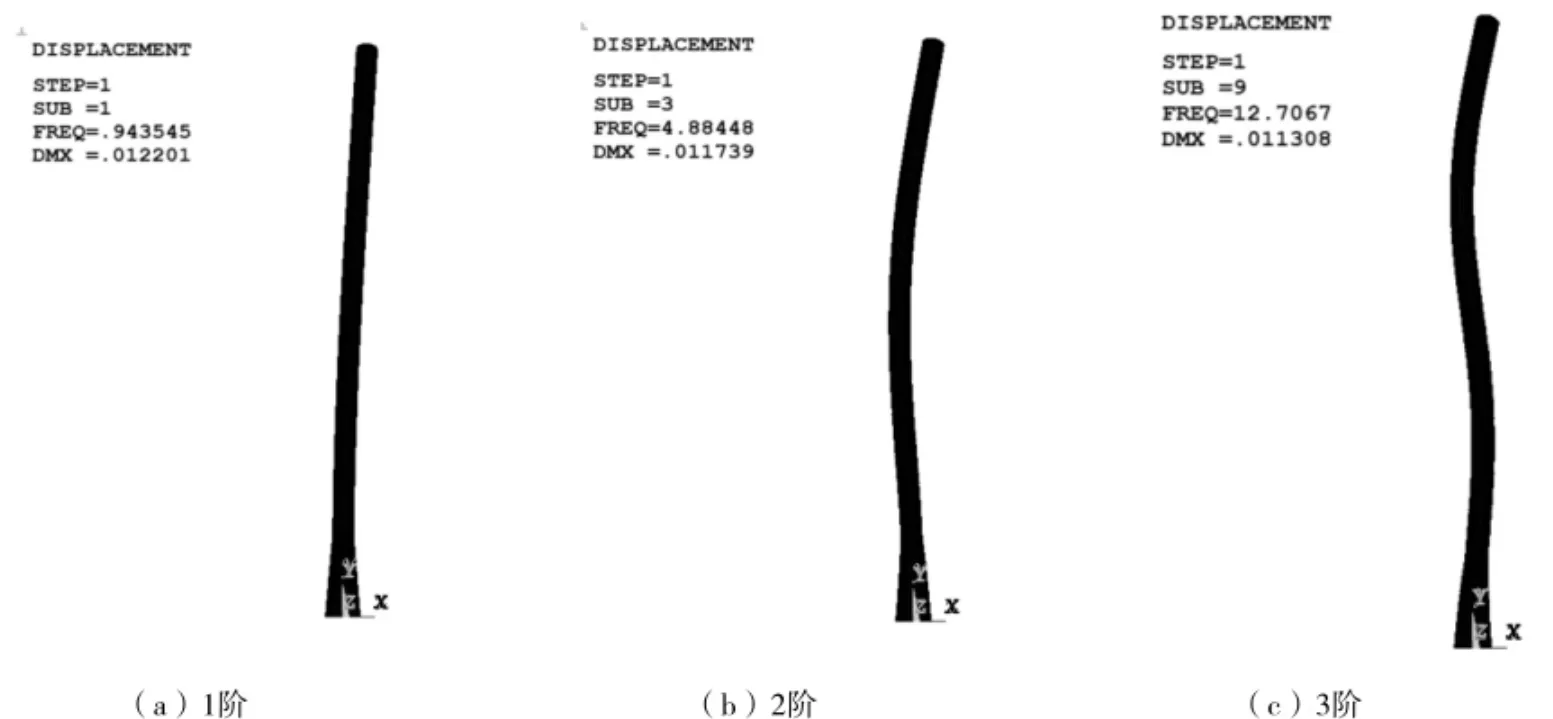
图2 空塔状态塔式容器通体模型下1阶～3阶振动特性图

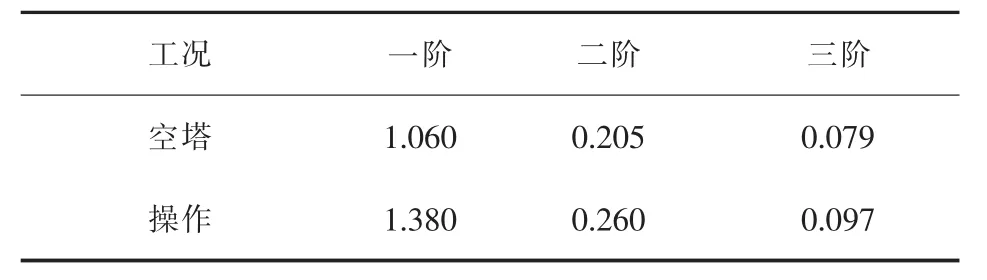
表2 模态分析得到的前3阶振动周期 s

由表2可知，空塔状态下第一阶振动周期为1.06 s，上文中采用SW6计算结果1.22 s与之的误差率为15%。同时，操作工况时的一阶振动周期1.38 s比空塔状态下的一阶振动周期1.06 s大。由此可见，同样条件下，塔体质量增大，振动周期随之增大。该塔的前三阶振动曲线与文献[3]附录B中曲线一致。

2.2 塔器横风向激励瞬态动力学分析

2.2.1 横风压

共振产生的横风向力可参照文献 [13]采用CFX流体计算方法得到，该方法可以得到较为准确的横向力幅值和直观的力分布。为简化计算过程，采用文献[5]中的公式计算：

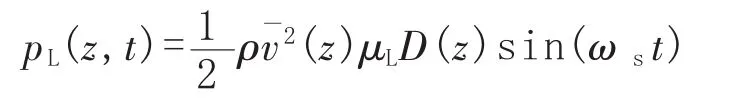
该公式也是NB/T 47041—2014中所采用的，能够满足工程上的使用需求。将塔任意高度z换成常用的符号h表示，得到高度h处的临界风速又已知涡流脱落频率 ωs=2fi，带入公式后得到塔任意高度风压值p(h,t):

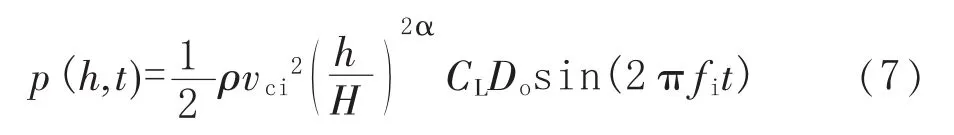
式中，h为设备任意位置高度，H为设备有效总高度，m； 指数 α 按粗糙度 A、B、C、D分别取 0.12、0.16、0.22和 0.3，本塔按粗糙度 B选取为0.16；fi为共振频率，Hz。

根据空塔分析的振动周期结果，可以得到vc1=8.6 m/s，在一阶临界速度下的雷诺数Re=1.08×106，CL取0.2。因振幅在1.3倍的临界速度下最大，所以将11.18 m/s代入式（7）计算，得设备受到的横向风压p(h,t)=28.5×(h/49.3)0.32×sin(5.93 t)。阻尼比按照式（5）计算得气动阻尼比 ξa=0.000 56， 其中 ma按照式 （3） 计算为591.7 kg/m。该乙二醇浓缩塔空塔时的一阶阻尼比为0.002 56。

在上述模型的基础上，瞬时动态分析使用最为精确的full法进行求解，假定风向为z轴的方向，所以在x轴方向施加横风向载荷p(h,t)。因为乙二醇浓缩塔的振动周期很小，设置的载荷步要足够小，计算出的振幅才能是准确的。

2.2.2 塔顶振幅

用乙二醇浓缩塔模型进行风载荷模拟，得到塔顶振幅随时间变化情况，见图3。由图3可以看出，塔的振幅由零逐渐增大，在80 s左右增加至最大值，随后按该振幅进行振动。最终得到的x向的振幅为0.335 m。该结果与现场的实际振幅情况吻合。当阻尼比为0.002 56时，使用SW6按NB/T47041—2014计算，得出的振幅为0.221 m,分析值为其1.52倍。这是NB/T47041—2014中未考虑在1.3倍的临界风速下的共振，所以NB/T 47041—2014的公式应予以一定的修正，以考虑苛刻的工况。

图3 乙二醇浓缩塔塔顶振幅随时间变化情况

2.2.3 轴向应力

风振需要校核的应力为图3上稳定振动最大振幅时间点82.47 s时刻对应弯矩所致的轴向应力，即是模型中的y轴应力。风振模拟得到的乙二醇浓缩塔模型塔体轴向应力分布见图4。由图4可知，最大轴向应力在裙座与下封头的焊缝处,最大压应力σ1=143 MPa，最大拉应力σ2=134 MPa。材料许用应力[σ]t=185 MPa，锥壳材料外压应力系数B=153 MPa。载荷组合系数K=1.2,进行应力校核，σ1＜K[σ]tφ=1.2×185×0.85=188.7(MPa)，σ2＜KB cos2β=1.2×153×cos24.8=182.3(MPa)。应力校核合格。

图4 乙二醇浓缩塔塔体轴向应力分布云图及裙座部分放大图

再对该处进行疲劳校核，对交变应力幅值考虑焊缝系数 K1=1.2[14]后计 算为 σalt=K1（σ1+σ2）/2=1.2×（143+134）/2=166.2(MPa)，查询 JB4732—1995《钢制压力容器——分析设计标准（2005年确认）》[15]中C-1疲劳曲线，得空塔运行状态下的循环振动次数N=6.5×104,已知振动周期为1.06 s，据此可计算得到允许连续振动的时间为19.1 h。乙二醇浓缩塔实际安装要数月时间，远超19.1 h的允许连续振动时间，所以安全隐患极大，必须采取相应的措施，如平台与塔同步安装、内部填料尽快装填、顶部增焊破风圈等，以避免连续振动的产生，防止设备变形及焊缝疲劳断裂。

2.2.4 操作工况风振

按上面的步骤计算设备操作工况振动情况，此时的临界速度6.61 m/s，设备受到的横风压为p(h,t)=16.78×(h/49.3)0.32×sin(4.55t)。 因操作工况下阻尼比不能准确计算，所以无法得出具体的振幅。比较可以看出，相比空塔工况时的情况，操作工况设备受到的横风压较小，阻尼比较大，振幅相应也较小。

推荐做法是，操作工况下，首先按照阻尼比0.01计算出塔式容器振动的斯科顿数Sc，然后根据Sc判断是否采取措施防止振动。

2.3 校核计算结果

对乙二醇浓缩塔横向风振校核计算工况及计算得到的临界速度vC、当量单位高度质量me、计算阻尼比ξ、分析计算的顶部最大振幅Y、按计算阻尼比SW6计算的顶部最大振幅Y1、标准阻尼比ξ0、按标准阻尼比标准计算的顶部最大振幅Y0、实际顶部最大振幅Y2、连续振动时间t进行汇总，见表3。

表3 乙二醇浓缩塔横向风振校核计算工况及结果汇总

3 结语

对安装期间发生明显振动的某乙二醇浓缩塔进行了横向风振校核计算和计算方法探讨，形成如下认识：

(1)空塔状态按ASME STS-1—2017计算阻尼比分析得到的顶部最大振幅与实际最大振幅的误差在10.5%～19.4%，按NB/T 47041—2014中阻尼比得到的振幅的误差在457%～642%。计算阻尼比更加接近填料塔的实际阻尼比，但若需要准确的值还需要一定的理论和数学模型的计算。同时，建议标准中振幅计算需添加修正系数，考虑到苛刻情况下1.3倍临界风速导致的最大振幅。

(2)空塔状态下斯科顿数Sc=2.94，按GB/T 50051—2021应安装减振装置，这与分析计算结果是一致的，需要考虑疲劳损伤。操作状态下斯科顿数Sc=5.08，按GB/T50051—2021应安装减振装置，或进行抗疲劳设计，给操作工况下塔器振动设计提供一定的参考。

（3）使用软件SW6计算,将计算阻尼带入得到空塔的最大振幅更接近实际的振幅，标准阻尼比得到的振幅不能反映空塔实际振动情况。同时斯科顿数Sc结果对于空塔计算具有正确的导向性，所以在不具备分析设计能力时，可采用计算阻尼比来计算空塔振幅，并进行相关强度校核，再使用斯科顿数Sc判定空塔状态下的安全性，从而判定是否需要添加扰流装置或减振控制系统。

（4）空塔结构与烟囱相近，上述计算的准确性仅针对空塔，特别是填料塔的空塔。板式塔有相对密集的塔盘支撑，空塔下可能会有较大的阻尼比。操作工况下的塔无法定量计算，文中计算不适用于操作工况。同时，本文的分析仅仅是个例的填料塔，所以仅作为工程设计过程的参考。