基于粒子群优化神经网络模型的BDS-3 卫星钟差预报
2023-02-16柴洪洲
王 旭,张 文,柴洪洲
(1.辽宁科技学院 资源与土木工程学院,本溪 117004;2.辽宁科技大学 土木工程学院,鞍山 114051;3.战略支援部队信息工程大学,郑州 450001)
在北斗(BeiDou navigation satellite system,BDS)精密单点定位中,主要通过获取GNSS 监测评估系统(international GNSS monitoring and assessment system,iGMAS)提供的钟差产品参与计算来实现实时精密单点定位[1]。目前,iGMAS 提供的BDS 实时超快速卫星钟差(iGMAS ultra-rapid,ISU),其观测部分(iGMAS ultra-rapid observe,ISU-O)和预报部分(iGMAS ultra-rapid predict,ISU-P)的精度分别为1ns 和10ns,均难以满足高精度实时精密单点要求。而iGMAS 提供的BDS 快速钟差产品和最终精密钟差产品精度虽然可以达到0.5 ns,但这两个星历分别需要经过17 小时和12天的延迟才能获取到,不具有很好的实时性[2]。因此,研究如何提高钟差产品质量或至少提高超快速钟差预报产品精度具有非常重要的意义。
小波神经网络(Wavelet Neural Network,WNN)由于具有良好的时频分析性能和有能力得到非平稳的结果而得到广泛的应用,这些特点使其在钟差预报中也取得了不错的成果[3-4]。但在实际的应用中发现,该模型在构造网络时需要随机选取网络参数,同时在网络训练过程中会出现局部极值而难以收敛到全局最优的现象。这会导致该模型每次钟差预报的结果有很大的不同,使得钟差预报结果不稳定;在实际中通常需要取多次预报结果的平均值作为最终的钟差预报结果,这样的结果在实际应用中是不理想的[5]。因此,本文针对这一问题,利用粒子群(Particle Swarm Optimization,PSO)算法优化小波神经网络网络参数,从而提高WNN 模型预报结果的稳定性,使其更好地应用到卫星钟差预报中。
1 粒子群优化算法
粒子群算法是以鸟类捕食为基础设计的一种群体智能的优化算法[6],通过随机产生一定规模的粒子对问题空间进行迭代搜索,得到优化结果。在粒子群优化算法中,每个问题的一个潜在解都与每个粒子一一对应[7],通过适应度函数计算的值来确定粒子的质量[8],粒子的速度决定了粒子移动的方向和距离。同时,在进行PSO 优化时,需要随机初始化每个粒子的位置和速度,并通过跟踪个体最优解pbest 和全局极值gbest 两个位置来更新自己。
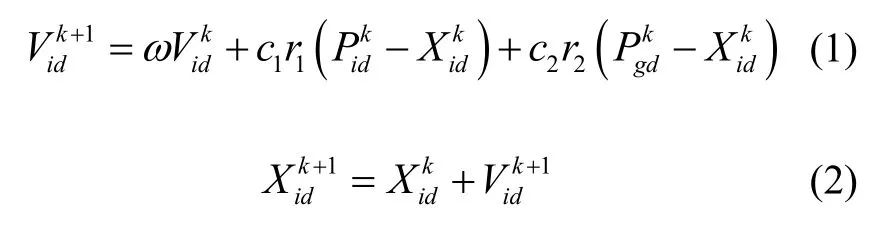
式中,ω为惯性权值,d=1,2…D,i=1,2…n,k为进化次数,Vid为粒子的速度,c1和c2为非负的常数,称为加速因子,r1和r2是取值为(0,1)的随机数。为防止粒子的盲目搜索,一般建议将其位置和速度限制在(-Xmax,Xmax)、(-Vmax,Vmax)区间。
小波神经网络学习过程主要是通过不断调整隐含层参数完成的,可将小波神经网络的各阈值和权值与粒子群算法中粒子位置一一对应,不断调整粒子的位置和速度向量,并通过式(1)(2)来进行迭代寻优,从而寻求最优网络的阈值和权值。这样做取代了传统网络仅凭借误差的传播来修正网络参数的缺点,降低了网络出现局部极值的概率[10],从而改善了小波神经网络预报结果不稳定的缺点。
2 钟差预报的PSOWNN 模型
WNN 模型的工作原理详见有关参考文献[11],在此就不再赘述了,本文主要详细说明适合钟差预报的PSOWNN 模型的构造过程。该模型构造过程包括以下几个步骤:
(1)小波基函数的选取。在小波函数的选择上,选择适合非线性时间序列预报的Morlet 小波函数。
(2)确定卫星钟差的学习样本,包括输入向量和期望输出向量。假设有L组卫星钟差数据并且每组数据包括N个元素,记作T=(t(1),t(2)…t(j)…t(L))其中,Y=(y(1),y(2)…y(j)…y(L)),其中y(j)∈RNt(j)∈RN;同时网络输出一个P维向量,记为
(3)粒子群优化网络参数。初始化网络参数,包括:设定伸缩因子aj、平移因子bj、网络连接权wi,j和wj,k、网络学习率η、动量系数α及容许误差ε。将向量{aj,bj,wi,j,wj,k} 作为粒子群算法里粒子的位置向量X。PSO 优化WNN 网络参数的具体步骤如下:
①初始化粒子群。对每个粒子的初始位置X和初始速度初始化,确定粒子群规模为m,设置最大优化次数k和粒子群算法的适应度函数f。适应度函数f选为小波神经网络的训练误差均方差:

式中,N是采样点个数,y(t)为第t的期望输出,为第t点的实际输出。
②利用粒子群算法的式(1)(2)在算法规定的最大值内不断更新粒子的速度和位置,并对更新后的位置进行记录。
③根据粒子的位置和训练样本,计算出每个粒子的适应度值,并更新当前个体极值Pi和全局极值Pg
④当误差达到最大值或者最初设定值时,进化停止,否则,返回第③步继续进行进化,直到满足精度要求为止,输出最优网络权值和阈值。
(4)网络训练方法的选取。网络在进行迭代训练时,通常对训练后的误差进行反向修正达到网络参数最优的目的[12],同时,采用成批训练样本的方法进行网络训练[13],WNN 模型具体训练步骤如下所示:
①将各连接权值和各阈值带入到小波神经网络中,并且设置训练迭代次数。
②自学习并且计算实际的网络输出向量,即:


④判断误差E和容许误差之间的关系:当误差E小于允许误差时停止迭代,网络训练结束;当误差E大于允许误差时并且未达到设定的迭代次数,则继续迭代。
⑤最后,网络的学习训练的相关参数通过误差E进行调整,具体的调整公式如下所示[11]:

第l次迭代时的网络参数可用式中表示。迭代结束后返回到第③步,直到误差E满足要求。
最后,由于输出的只有钟差数据一种类型,因而输出层的节点确定为1。通过实验尝试,最大的训练次数设1000 次,模型预报效果最好。对于隐含层的神经元个数为6 时[14],钟差预报得到的效果最好。另外,本文所设计的粒子群算法中,种群规模设为20,惯性权值设为0.8,加速因子和设为1.45,进化次数设为100。粒子群优化小波神经网络流程图如图1 所示。

图1 粒子群小波神经网络的工作流程Fig.1 Algorithm flowchart of the PSOWNN
3 算例与分析
为了验证文中提出方法的有效性,本文使用iGMAS 提供的BDS week 791 第二天15 min 采样间隔的快速卫星钟差进行实验分析。选取所有BDS-3 数据完整的卫星进行实验,表1 给出了当前使用的BDS-3卫星钟类型[15]。最后,以预报时间段对应精密钟差数据为基准,使用表征预报精度的均方根误差(RMS)和反映预报稳定性的极值(Range)为统计量[11],比较分析模型预报的效果。

表1 BDS-3 卫星钟类型Tab.1 On-board clock of BDS-3 satellites
3.1 算例一
首先对比WNN 模型和PSOWNN 模型预报性能。随机选取氢钟和铷钟的各2 颗卫星进行预报实验,文中选取PRN19、PRN21、PRN26、PRN34 四颗卫星。利用24 h 的钟差数据建模训练,预报接下来6 h 的钟差,图2 给出了4 颗卫星使用粒子群算法优化过程中最优个体适应度值变化曲线。
从图2 中可以看到,粒子群算法得到的最优个体适应度最小值与0 非常接近,并且有很快的收敛速度。表2 给出了4 颗卫星使用粒子群优化算法得到最优个体适应度的统计值。
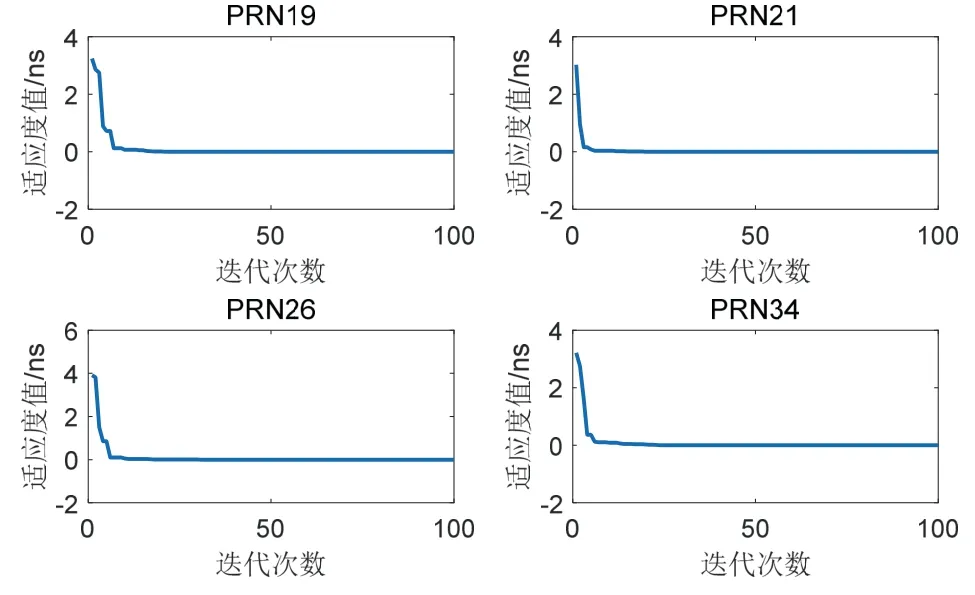
图2 PSO 算法最优个体适应度值变化曲线Fig.2 The variation curve of fitness value of the optimal individual for PSO

表2 最优个体适应度的统计值(单位:ns)Tab.2 Statistical values of the optimal individual fitness based on PSO(Unit: ns)
从表2 可以看到,PSO 在对WNN 模型参数进行优化时,在进化20 次以内就可以得到最优个体适应度值,并且最优个体适应度值都在0.001 左右,接近于0。这说明粒子群算法具有较强的函数极值寻优能力。另外,本文还给出了WNN 和PSOWNN 两种模型训练误差曲线的对比情况(图3)以及两种模型5 次预报结果RMS 变化情况(表3)。
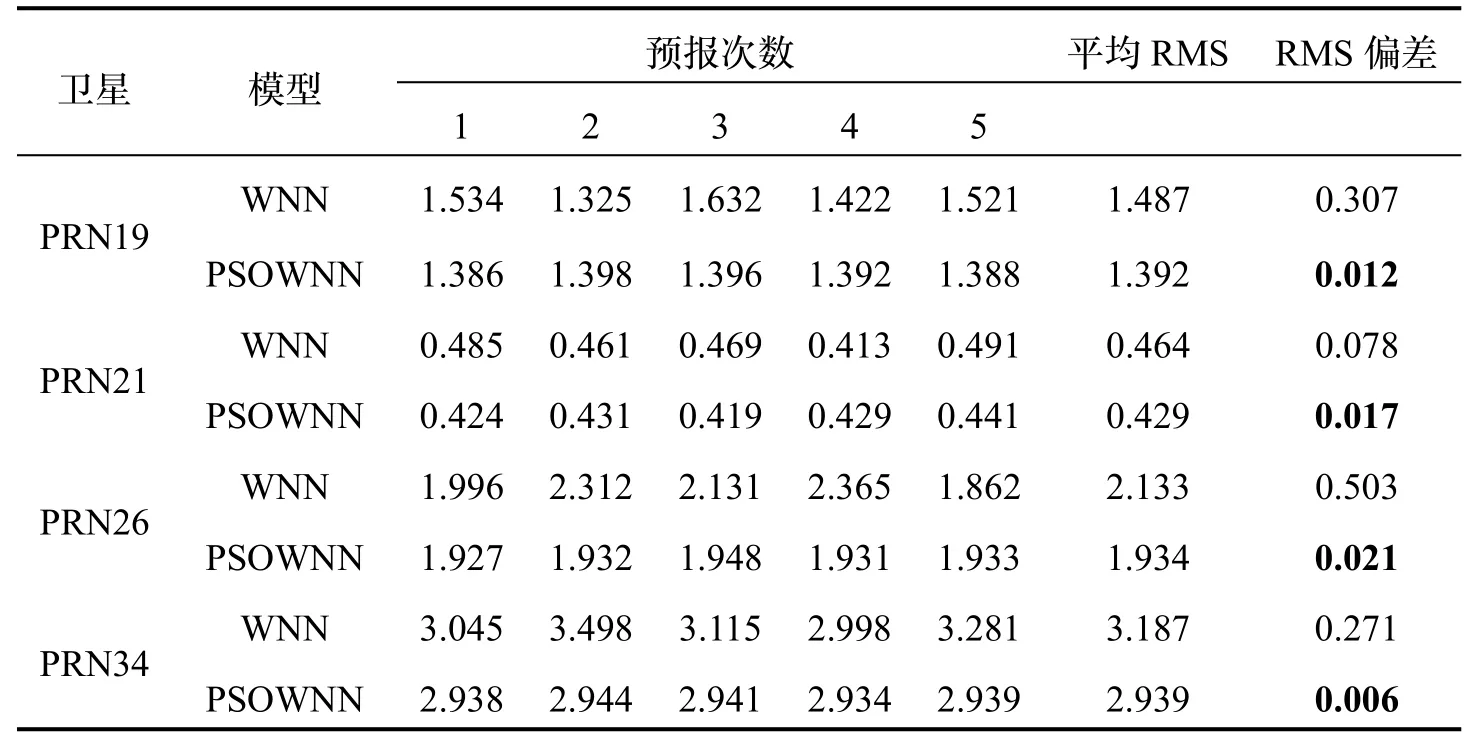
表3 两种模型5 次预报的平均统计值/nsTab.3 Statistics of the five times predictions of the two models/ns
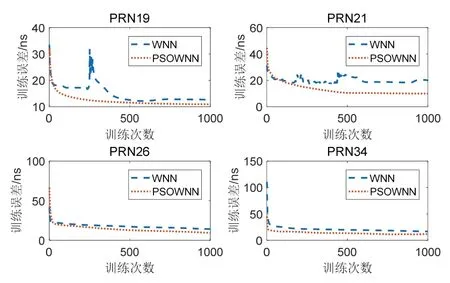
图3 两种模型训练误差曲线Fig.3 Variation curves of the training errors of the two models
图3 可以看到,对4 颗卫星进行预报时,PSOWNN模型训练误差小于WNN 模型,并且随着训练次数的增加收敛的速度明显高于WNN 模型。同时发现,对PRN19 和PRN21 两颗卫星预报时,WNN 模型在训练过程中误差曲线出现局部极值振荡的现象。另外,通过两种模型预报5 次的统计值可以发现,WNN 模型预报5 次结果的RMS 平均值大于PSOWNN 模型,同时预报结果的RMS 偏差范围较大,最大的偏差值已经达到了0.5 ns。说明WNN 模型在训练过程中会受到局部极大值或极小值的影响,会导致每次钟差预报得到的结果不是很稳定。而PSOWNN 模型5 次预报结果的RMS 值变化不大,偏差范围较小,均在0.02 ns之内。说明WNN 模型构造参数经粒子群算法优化后,降低了网络在训练中出现局部极值的概率,改善网络随机选取参数对预报结果的影响,提高WNN 模型预报结果的稳定性。也就是说,PSOWNN 模型预报一次的结果就可以作为钟差预报的最终结果,不需要进行多次预报取最优值作为最后的预报结果,改善该模型实际应用性。另外还要说明一点,在对PRN19、PRN21、PRN26 三颗卫星预报时,出现了一次WNN 模型预报的结果好于PSOWNN 模型。出现这样结果的原因是WNN 模型在训练过程中随机选取的参数没有导致网络训练出现极值,并且随机选取的参数适合卫星钟差数据,使WNN 具有较好的预报效果。但是这样的情况在5 次实验中也仅仅出现了一次,说明了网络训练过程中随机选取参数会使网络预报结果的不稳定。
2.2 算例二
为了全面分析PSOWNN 模型预报的性能,对18颗DBS-3 卫星钟差进行12 h 和24 h 的预报实验。考虑文章的篇幅,这里仅给PSOWNN 模型与常用两种预报模型对PRN19、PRN21、PRN26、PRN34 四颗卫星预报24 h 的预报效果(图4 和表4),图5-6 和表5给出了其余卫星预报不同时长的平均统计值。

图4 三种模型预报误差Fig.4 Prediction error of three models

表4 四颗卫星预报24 小时结果统计值(单位:ns)Tab.4 Statistics of prediction result of the four satellites in 24 hours(Unit:ns)
由图4 和表4 可知,PSOWNN 模型预报的误差小于两种常用模型。对于GM(1,1)模型来说,对BDS两颗氢原子钟的预报精度和稳定性好于两颗铷原子钟,而PSOWNN 正好相反,对铷原子钟的预报效果好于氢原子钟。QP 模型对不同类型卫星钟预报的效果没有出现其他两种模型的现象,对PRN21 预报的效果最好,对PRN19 预报效果最差。图5 给出了三种模型对18 颗卫星两个时段预报结果统计对比情况,图6给出了预报24 h 三种模型对18 颗卫星结果统计对比情况,表5 给出了按原子钟类型进行分类的预报结果统计值,其中铷钟和氢钟的RMS 和Range 分别是其所对应卫星RMS 和Range 之和的平均值,“All”表示所有卫星预报的RMS 和Range 的平均统计值。
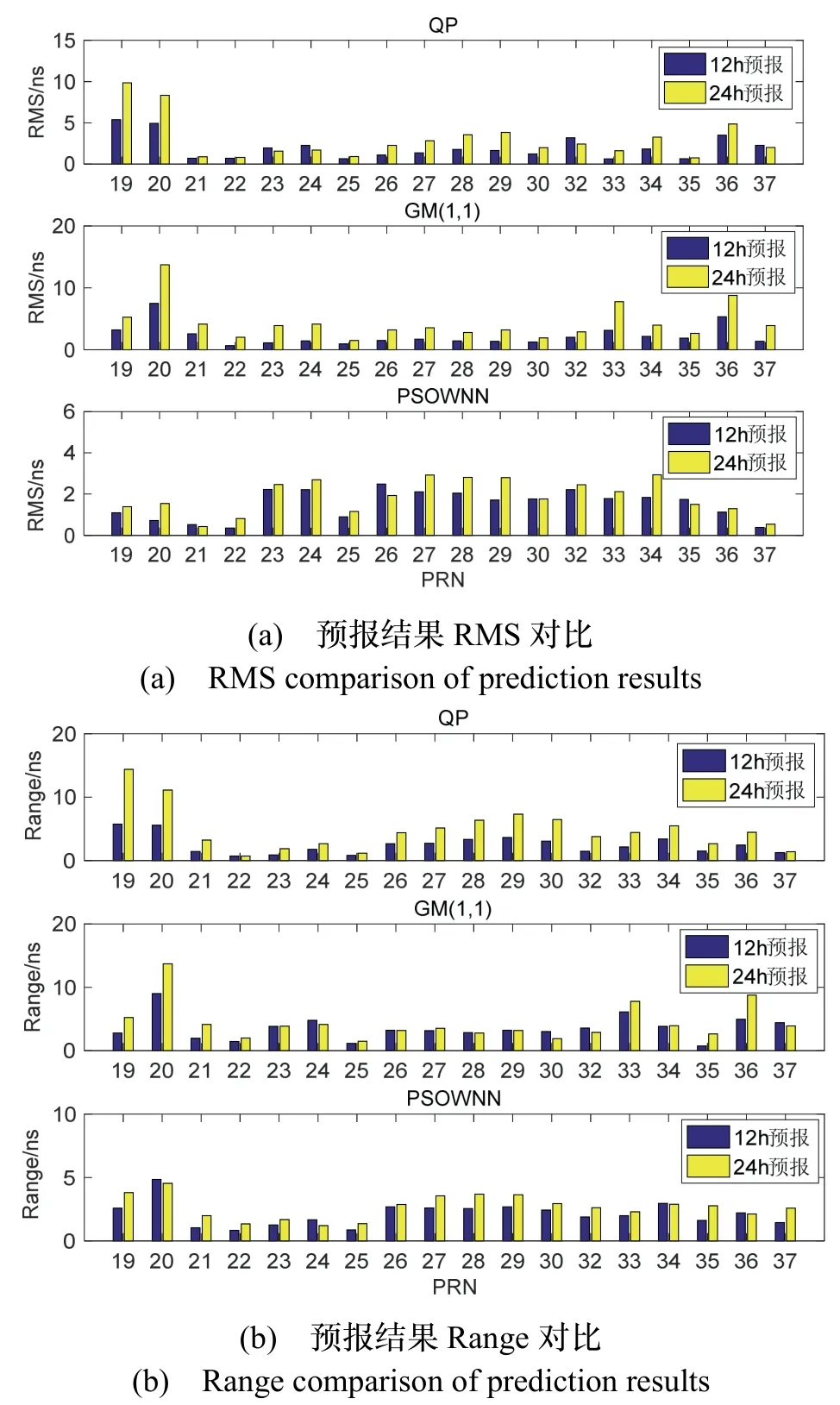
图5 三种模型预报两个时长的结果对比Fig.5 Comparison of prediction results of three models in 2 periods

图6 三种模型24 h 预报的结果对比Fig.6 Comparison of Prediction results of three models in 24 hours
从各卫星两个时长预报RMS 和Range 图可以看出,三种模型均出现了随预报时长的增加预报效果变差的现象。但从RMS 和Range 值上看,PSOWNN 预报的结果变差的幅度要明显小于两种常用模型,预报的稳定性更好。
从图6 和表5 可以看到,总体上,在24 小时预报中,本文所建PSOWNN 模型预报的精度和稳定性均优于两种常用模型。相比于两种常用模型预报的精度分别提高了约49.7%和66%。对于不同类型原子钟预报结果而言,QP 和GM(1,1)两种模型对氢原子钟预报效果优于对铷钟预报的效果,出现这样情况的原因可能是氢原子的性能优于铷原子钟,导致两种模型对氢原子钟卫星的钟差预报效果相对较好。而PSOWNN 模型对两种类型原子钟预报的RMS 和Range 值变化不大,这说明该模型不会受星载原子钟类型的影响,对不同类型的原子钟均具有较好的预报钟差能力。另外,无论对于氢钟还是铷钟来说,三种模型预报的精度明显好于ISU-P 产品,PSOWNN 模型提高的幅度最大,相比于ISU-P 产品预报精度提高了97.7%。这是因为,三种模型所使用的建模数据均为快速钟差产品,而ISR 产品的质量优于预报ISU-P 产品的建模数据(ISU-O),所以三种模型预报的精度要优于ISU-P 产品。在实际的应用中,可以使用ISR 钟差产品数据建模来获得更高质量的钟差产品。

表5 四颗卫星预报24 小时结果统计值(单位:ns)Tab.5 Statistics of prediction result of the four satellites in 24 hours(Unit:ns)
4 结论
为了解决小波神经网络预报钟差结果不稳定的问题,本文建立一种粒子群优化小波神经网络钟差预报模型,该模型通过粒子群算法确定网络的最优参数,解决了网络训练出现极值导致每次预报结果有很多差异的问题。通过实验算例验证了该方法所得到的钟差预报结果稳定,每次钟差预报结果的偏差范围在0.02 ns 之内,且预报的精度优于两种常用模型及iGMAS 提供的超快速钟差产品,这些特点让该方法在钟差预报中得到更好的应用。
