基于PSO 的建筑工程资源均衡优化研究

唐 剑，曹晶莹，王鹏杰

（江西科技师范大学土木工程学院，江西 南昌 330013）

1 前言

20 世纪50 年代中后期，随着现代工程项目管理的兴起，网络计划被广泛应用，并被认为是一种科学、行之有效的管理手段。但大多数工程初期的网络计划通常存在问题，即难以估计在项目实施过程中可能发生的意外以及消耗的时间和资源。资源管理是建筑工程项目管理的三大目标之一，资源均衡是一种有效的资源管理方法。近年来，国内外学者对资源优化问题的研究已非常深入。Alvarez-Valdes[1]采用精确算法提出优化模型，并通过案例进行分析验证。S.Kumaman 等学者[2]使用不同的启发式算法，并对其最优解进行验证。王文军等学者[3]改进了多目标粒子群算法，并将其与NSGA-Ⅱ进行对比,以证明其可行性及优越性。谢存仁[4]在资源价格变动的基础上，建立了工期最短-资源均衡多目标优化模型，该模型为项目管理人员制定合理的施工计划提供参考。刘新博等学者[5]提出以工期最短、资源均衡为目标的施工项目多目标调度优化问题，利用有向无环图描述工程项目，并与资源约束相结合，构造数学模型。孔峰[6]针对实际情况中考虑资源投入的必要性建立了一种以资源投入为变量的基于广义资源日历约束的项目调度优化模型，并通过案例验证了模型的准确性和高效性。邹豪波[7]以工期和费用的双目标权衡为目标构建问题数学模型，设计基于个体多样性自适应和动态拥挤度的改进遗传算法，并用实例验证了算法的收敛性。Ammar Mohammad A[8]将LOB（Line of Balance）方案下的资源均衡与分配问题建模为保证最优解的优化问题。本文针对工期固定，多资源均衡优化问题，先利用层次分析法对各资源赋予权重，以最小方差为目标函数作为评价指标，运用微粒群算法进行优化，最后通过实际案例验算，完善工程网络计划优化模型。

2 改进的微粒群算法

微粒群算法（Particle Swarm Optimization，PSO）源于鸟类的觅食行为。PSO 将每个微粒视为一个潜在解，其适应度值由适应度函数确定，微粒速度决定其飞行方向和距离[9]。PSO 在给定解空间随机初始化，并依据被寻优问题变量个数确定解空间的维数。在N 维目标搜索空间中，M 个微粒构成一个种群，第i 个微粒表示N 维的一个向量，即Xi＝（xi1，xi2，……，xiN），i＝1，2，……，M。第i 个微粒的速度是一个N 维向量，记为Vi=（vi1，vi2，……，viD），i＝1，2，……，M。每次迭代微粒都会跟踪个体极值和全局极值。目前为止，第i 个微粒所找到的最优位置即为个体极值，即Pbest=（pi1，pi2，……，piN），i＝1，2，……，M；整个种群目前所能找到的最优位置即为全局极值，即gbest=（g1，g2，……，gN）。

在觅食过程中，个体自身的认知惯性通常会干扰其调整自身计划。在PSO 改进过程中，需要在微粒速度更新公式中引入惯性学习因子，以充分利用算法中自我认知部分和社会认知部分，从而对算法的优化效果产生一定的影响。

其中：ω 为惯性权重；c1和c2为学习因子，即加速常数；ω1，ω2表示惯性学习因子；r1、r2∈[0，1]，增加微粒飞行的随机性，i＝1，2，…，N；vij为微粒速度，vij∈[-vmax，vmax]，vmax是常数，用来限制微粒速度。

PSO 具体流程如下：

（1）初始化微粒群的群体规模M，微粒位置xi，速度vi。

（2）计算微粒的适应度值fit[i]。

（3）比较fit[i]和pbest（i）。若fit[i]＜pbest（i），则用fit[i]代替pbest（i）。

（4）比较fit[i]和gbest。若fit[i]＜gbest，则用fit[i]代替gbest。

（5）迭代更新vi和xi。

（6）处理边界条件。

（7）判断是否满足终止条件：若是，结束算法，输出结果：否则返回步骤（2）。

3 多资源优化原理及步骤

3.1 多资源相对权重的确定

建筑工程项目的执行，往往涉及多种资源，重要性不尽相同，须按照各种资源的重要性程度确定其相对权重，从而实现多资源的均衡优化。利用层次分析法（Analytic Hierarchy Process）确定资源的相对权重。利用九标度法将资源进行两两比较，构建资源重要性判断矩阵，并采用特征根法确定资源的相对权重。

3.2 同一化多资源

假设一个建筑工程施工项目中某个工序需要Z种资源，工作（i，j）单位时间内对第a 种资源的需用量为r（i，j，k），第t 时间段内，工程对a 资源的总用量为：

式中W——网络计划中所有工作的集合；

由于不同时期的工程所需的资源不尽相同，需对资源需用量进行同一化处理后才能使其具有可比性。将各种资源同一化为相同数量级，将资源的需求转变为相对需求。

tm——工程的终止时段；

同一化处理后，第t 时间段，工程对a 资源的相对需求量为：

工程施工阶段，资源用量均保持在0～1 之间，使资源用量具有可比性。

3.3 等效资源相对需用量

项目施工时，考虑到每种资源的相对重要程度，将单位时间内各资源的相对需用量，进行加权求平均值，即：

ωa——a 资源的权重；

3.4 多资源均衡优化步骤

①运用AHP 法，确定资源相对权重；

②同一化资源；

③求出资源相对需求均值；

④从网络计划图的终止节点开始，逆箭线方向进行调整。

⑤按上述步骤调整工作的开始时间，直至无法调整。此时资源均衡效果最好。

4 资源均衡优化的数学模型

进行资源优化时，首先计算工作的时间参数，逆箭线方向调整工作的开始时间，直至所有工作均无法调整。在工程建设中，资源用量具有较大波动性。资源动态曲线上，当天各工序资源需求量叠加的影响，造成资源需求量的高峰值和低谷值，需优先调整资源需用量较大的工作。模型的目标函数为资源需求量方差σ2，约束条件为工作时间限制及资源需求限量。

式中：j=1，2，……，m；i∈p（j）；m 为工作数；Rt为第t 日资源用量；Rm为资源日均用量；Ti为工作i的实际开始时间；Rit为工作i 在第t 日的资源用量；R 为每日的资源限量；p（j）为工作j 所有紧前工作。值最小时，σ2最小，资源均衡性最好。

5 案例分析

某工程项目施工方案见图1，共包含10 项工作（记为工作A、B、C、D、E、F、G、H、I、J），消耗3 种资源（记为资源1、2、3），资源日均消耗量为箭线上方数字，工作持续时间为箭线下方数字。

图1 双代号网络计划及工序资源消耗量图

（1）运算中设定学习因子c1，c2的值为2，进化代数为500，3 种资源的权重分别为0.11，0.26，0.63。

（2）资源相对需求量见表1。

表1 资源重要性比较标度

（3）等效资源相对需用量见表2。

表2 等效资源相对需求表

（4）计算项目等效资源相对需用量的平均值。

（5）计算结果表明第4 天至11 天等效资源相对需求量大于，优先调整该时间段对应工作的开始时间。

（6）由图1 可知①②⑤⑧为该项目双代号网络计划图的关键线路，关键线路上关键工作的TFi-j和TTi-j均为0，不能调整；需优先调整非关键工作B、C、E、G、I、G。

（7）优化前后的网络计划见图2 和图3，各工作的时间参数及优化后的最早开始时间见表3。

表3 参数及其优化解

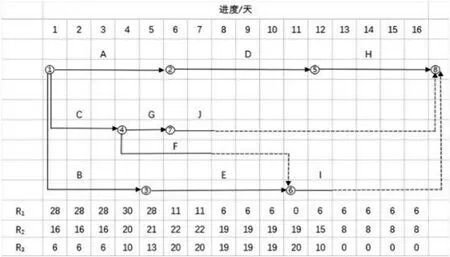
图2 双代号时标网络计划图

图3 优化后网络计划图

由表4 数据可知资源1 优化前资源强度方差为109.81，最优方案的资源强度方差为74.31，降低32.33%；资源2 优化前资源强度方差为25.38，最优方案的资源强度方差为2.38，降低89.15%；资源3优化前资源强度方差为62.25，最优方案的资源强度方差为22.5，降低63.86%。资源1、2、3 的优化效果见图4、图5 和图6，资源消耗强度更均衡。

表4 资源均衡优化效果

图4 资源1 优化前后的每天消耗强度折线图

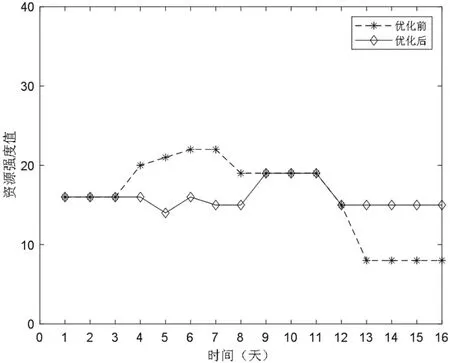
图5 资源2 优化前后的每天消耗强度折线图

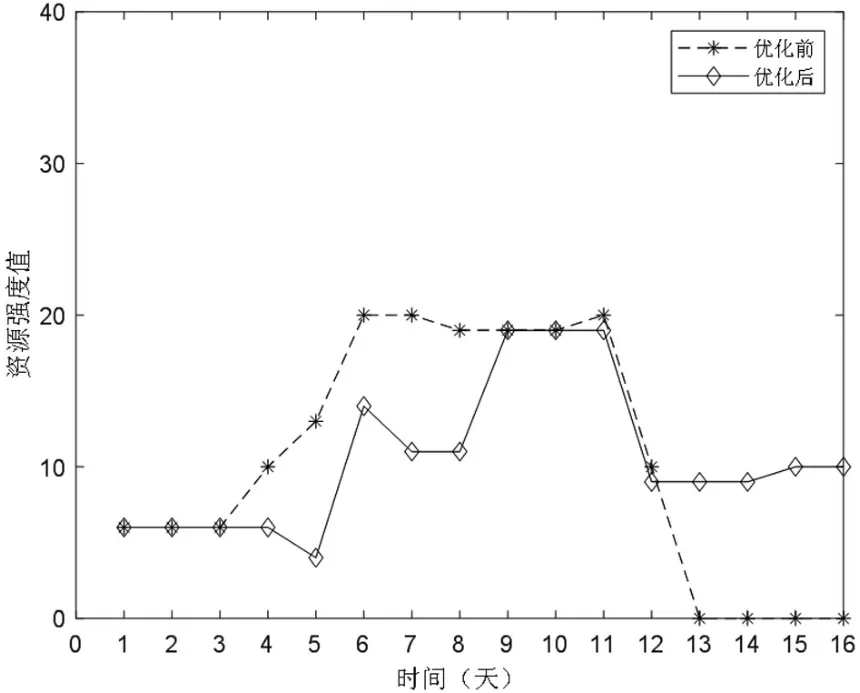
图6 资源3 优化前后的每天消耗强度折线图

6 结论

通过对施工进度的优化，达到资源均衡的目的。首先，将非关键工作的开始时间作为变量，构建以资源均衡优化为目标的数学模型；其次，采用改进PSO 对模型进行求解；最后，结合实例，验证模型的可行性。该方法可为科学地确定工程施工中非关键工作的开工时间提供借鉴，帮助施工企业更好地进行资源调度，合理使用资源。而工程施工中，要根据施工现场调整施工进度，例如，非关键工作的持续时间会有所变动，可对其进行分割或搭接，从而限制资源的进一步均衡优化。本文所述算法仍具改进空间，进一步提高其实用性。