承德市某片区海绵城市雨水径流及暴雨分析

王景浩

(河北省承德水文勘测研究中心，河北 承德 067000)

1 概述

水资源是生态环境健康发展与经济社会运行、民生安全的必备基础资源。近年来，随着经济快速发展、城镇化加剧、人口增加，水资源需求量与日俱增，我国北方地区水资源短缺已成为限制区域可持续发展的重要因素[1-2]。海绵城市是指在城市建设过程中优化地面及给排水管道设计与建设，强化地面雨水的渗透与净化，进一步优化城市给排水管道，实现对雨水的利用。雨水径流及暴雨分析对城市雨水排水系统的设计十分重要，且设计流量的合理计算又直接取决于所采用的雨型强度公式。作为承德市城镇排水管网设计的重要参考指标，不同降雨重现期下的暴雨强度及雨型分析对海绵城市设计具有显著影响。

作为国内外海绵城市排水工程设计过程的重要分析方法，暴雨强度公式及芝加哥雨型模型广泛被地应用于国内外海绵城市排水工程分析过程[3]。Kwan Tun Lee[4]等运用研究区域内台风暴雨的降雨资料及芝加哥计算法报道了从降雨强度-持续时间-频率曲线推导出的一个持续时间为48h的双三角形设计水位线，并据此模拟强台风暴雨的时间分布影响。研究结果表明：在指定的降雨重现期条件下产生的设计流量接近使用流量记录的频率分析获得的流量。Batchabani[5]等运用加拿大研究区域的降雨资料及芝加哥计算法评估了Riviere des Prairies流域的水文和环境影响。研究结果表明：为减轻研究流域洪水的潜在影响，应在此区域采取预防措施。苏海龙[6]等使用过芝加哥雨型计算法及SWMM模型对西安小寨区域现状管网能力评估及积水点分析，研究结果表明：芝加哥法具有良好的通用性，可以高效准确地分析西安小寨区域在降雨历时内的暴雨强度，并为后续海绵城市设计提供基础数据。邓培德等[7]利用芝加哥雨型概念推导出三维参数雨型，并据此提出同频率控制的模式雨型。

然而尚未有利用暴雨强度公式及芝加哥雨型法分析不同降雨重现期及雨峰位置(r)下承德市暴雨强度及雨型分析的报道。综上所述，本文结合承德市某研究区域内海绵城市系统工程项目，对研究区域内的不同降雨重现期下的雨水径流及暴雨雨型进行分析。研究结果对承德市片区海绵城市雨水排水系统设计提供可靠的理论依据。

2 研究区域概况

承德市地处河北省东北部，处于华北和东北2个地区的连接过渡地带，地近京津，背靠蒙辽。地区地貌主要由坝上高原和燕北山地2部分组成，高程介于212～2118m之间。坝上高原位于承德地区的西北部，是内蒙古高原的南缘部分，海拔高度多在1000～1700m之间。围场坝上地势平缓，主要由疏缓丘陵和坝缘山地，及波状高原组成。中部为丘间宽广谷地，北部也有固定，半固定沙地。冀北山地，海拔高度1300～1500m。研究区域位于河北省承德市东北部地区，总面积约为17.6km2，海拔在1502～1620.1m之间。研究区域位置如图1所示。

图1 研究区域位置

3 研究地区暴雨强度公式

承德地区境内自然资源丰富，有滦河、潮-白河、辽河4大水系，年产水量37.6亿m3，是京津唐的重要供水源地。年降水量多介于418～650mm之间，多年平均值为530.1mm，水资源较为匮乏[1]。近18年来承德市地表水资源量最高值为2012年的26.22亿m3，最低值为2002年的6.07亿m3，平均值为14.75亿m3。研究区域6—9月3个月降水量一般达到年总降水量的60%～80%[8]。因此，根据研究区域不同重现期的暴雨强度，合理规划雨水排水系统的设计方法和设计规模，提升研究区域雨水利用效率，进一步提高承德市排水蓄水能力。承德市气象部门联合当地住建部门颁布的暴雨强度公式，为承德市城市雨洪建设提供重要设计依据。承德市的暴雨强度公式如下：

(1)

(2)

式中，i—暴雨强度，mm/min、mm/ha；t—降雨历时，min；P—重现期，年。本次计算降雨历时t取120min，重现期P取1、2、3、5、10、20、30、50、100年。计算结果见表1。

表1 承德市不同降雨重现期下降雨强度表 单位：mm/ha

4 研究区域降雨量模拟

4.1 芝加哥雨型模拟方法

芝加哥雨型计算法因其相对较高的普适性，被广泛地应用于国内海绵城市降雨分析过程[9]。我国国内行业标准及地方雨量分析规定等也广泛地采用该方法。芝加哥雨型计算法是美国人Keifer、Chu研究出的一种应用在排水管网系统的雨量分析理论，该理论把平均强度转化成瞬时强度，进一步通过人工造峰即可求得，其中雨峰位置和研究区域的气候及水系情况相关。目前，常见的雨型分析方法有：常数法、三角法、德波尔德法(Desbordes)、芝加哥法(Chicago)、西法尔达法(Sifalda)、水土保持服务水位图(Soil conservation service hyetograph)等[6]，作为一种可以应用在大流域范围内的雨量雨型分析理论，芝加哥雨型计算法被广泛地应用于“海绵城市系统设计”及“排水系统设计”过程中。

4.2 芝加哥雨型计算法原理

芝加哥雨型计算公式如下：

(3)

式中，t—降雨历时，min；q—平均降雨强度，mm/min；A，b，n等均为地方降雨参数。进一步求得降雨历时t的总降雨量：

(4)

式中，H—降雨总量，mm。t时刻的降雨强度为：

(5)

t=ta+tb

(6)

(7)

(8)

(9)

式中，r—雨峰相对位置参数，一般取值为0.3～0.5；tb—峰后降雨历时，min；ta—峰前降雨历时，min。qa、qb—峰前、峰后降雨强度，mm/min；C—地方观测经验值。根据相关文献报道[9-10]，本研究模拟过程雨峰位置选取为0.4。

4.3 暴雨强度计算分析

基于承德市暴雨强度计算公式，计算了1、2、3、5、10、20、30、50、100年重现期下的暴雨强度值，暴雨历时为120min。结果如图2所示。

图2 研究区域内暴雨强度

根据图2及表1可以发现，在降雨历时区间内(0～120min)，暴雨强度随着重现期的增加而逐渐提高。当降雨历时为40min时，对应各重现期下的暴雨强度值分别为：92.72、128.50、149.43、175.80、211.58、247.36、268.29、294.66、330.45mm/ha。降雨重现期100年与1年的暴雨强度比值为3.56。随着降雨历时的增加，承德市暴雨强度在0～55min内迅速降低，并于60～120min后变化逐渐趋于平稳。具体来说，随着降雨重现期从100年降低到1年，经历120min降雨历时的暴雨强度从138.02mm/ha降低到38.73mm/ha。120min降雨历时下的最大暴雨强度与最低暴雨强的比值依然保持为3.56。

进一步地，对研究区域内降水量进行计算。见表2，在研究区域内的汇水量分别为：681.56、944.59、1098.45、1292.30、1555.33、1818.35、1972.22、2166.06、2429.09mm。根据项目所在地暴雨强度分析可知，随着降雨重现期增加，暴雨强度及研究区域的雨水径流汇水量将出现明显上升。

表2 降雨量统计表

4.4 芝加哥雨型分析

根据芝加哥雨型的分析公式，进一步通过积分计算研究区域芝加哥综合暴雨过程线[10]。如图3所示，在降雨历时内且降雨重现期为1、2、3、5、10、20、30、50、100年的条件下，雨峰位置下(48min)的暴雨强度分别为：1.3364、1.8521、2.1538、2.5339、3.0496、3.5653、3.8670、4.2471、4.7628mm/min。在该雨型条件下，暴雨强度最高值与最低值比值为2.56。在本研究条件下，承德市东北部研究区域内雨峰位置下暴雨强度均表现出先增加后降低的趋势，且随着暴雨重现期的增加，暴雨的强度逐渐增加。

图3 不同降雨重现期下的雨型

如图4所示，在降雨重现期为20年的条件下，随着雨峰位置参数(r)从0.30逐步提高到0.70，芝加哥雨型下雨峰位置的出现随降雨历时出现明显的滞后。具体来说，雨峰位置的出现时间从36.0min增加到84.0min。基于上述分析，在承德市研究区域内进行的雨水蓄排系统工程设计中，应根据历年降雨数据合理选择降雨重现期及雨峰参数，据此合理计算雨水径流时间，并设计雨水蓄排构筑物体积。

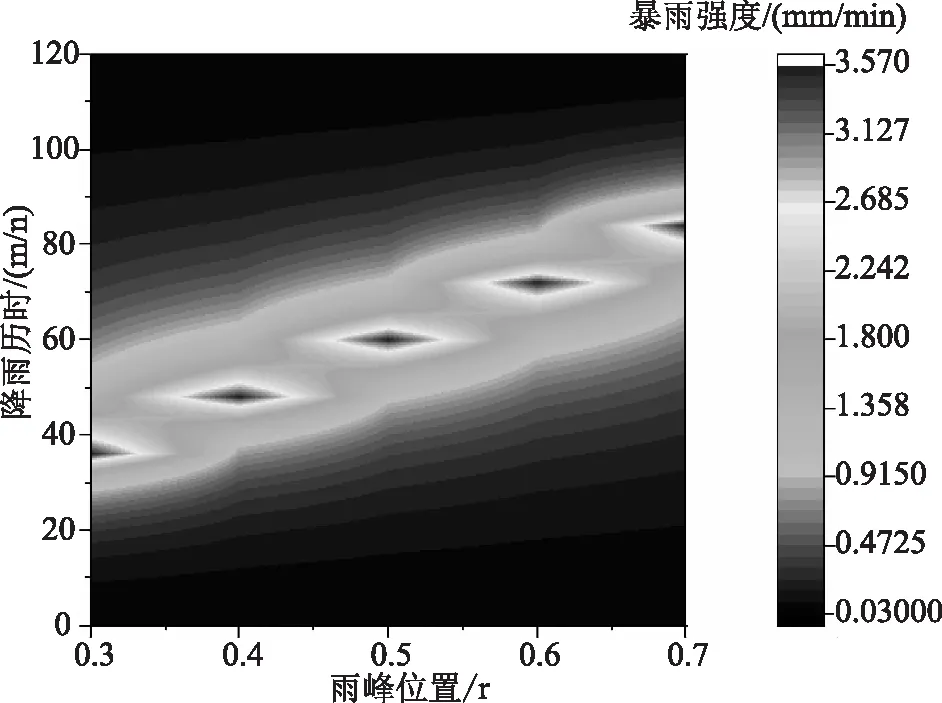
图4 不同雨峰位置下的雨型

5 结论

本研究运用承德市暴雨强度公式及芝加哥雨型分析方法，对海绵城市概念下不同降雨重现期及雨峰参数条件下研究区域内的雨水径流及暴雨进行分析，得到了如下结论。

(1)随着降雨历时的增加，不同降雨重现期下的暴雨强度之间的最大比值为3.56。

(2)随着雨峰参数(r)的提高，研究区域内的最大暴雨强度出现时间分布发生了明显的滞后，且暴雨雨型整体呈现出先增加后降低的趋势。

(3)结合降雨峰值数据可知，在承德市研究区域内进行的雨水蓄排系统工程设计中，应根据历年降雨数据合理选择降雨重现期及雨峰参数，据此合理计算雨水径流时间，并设计雨水蓄排构筑物体积。