考虑高频损耗的ZPW-2000A轨道电路暂态响应分析
2023-02-15欧静宁于光昊
赵 斌,陈 磊,欧静宁,王 东,于光昊
(兰州交通大学 自动化与电气工程学院,甘肃 兰州 730070)
轨道电路作为自动、连续监测线路占用情况的基础设备,具有调整、分路、断轨3 种工作状态,当有列车占用轨道区段时轨道电路的工作状态须对应准确显示。然而,分路不良现象时有发生,严重时会危及行车安全。近年来,利用轨道电路的暂态响应判别工作状态的变化成为研究的课题,因此,准确分析轨道电路的暂态响应尤为重要[1]。
目前,针对轨道电路暂态响应的研究,主要基于时域有限差分法计算接收端轨面电压。时域有限差分法,是用中心差商代替场量对时间和空间的1阶偏微商,通过在时域内的递推和迭代得到计算结果[2]。由于ZPW-2000A 轨道电路模型中存在补偿电容、调谐单元等集总参数元件,不能直接利用时域有限差分法计算接收端轨面电压,需要将轨道电路模型分为传输线和集总参数元件2 个部分单独迭代计算,计算过程复杂[3]。另外,考虑高频损耗时,采用时域有限差分法时需要利用矢量匹配法对参数进行拟合,根据得到的极点、留数和常数项推导轨道电路的有理近似函数,再基于分段线性递归卷积推导轨道电路两端的电压和电流关系,结合离散方程最终得到轨道电路接收端轨面电压[4],推导过程复杂,且计算难度大。
本文采用傅里叶变换结合Q-D 算法分析高频损耗下的ZPW-2000A 轨道电路暂态响应。根据ZPW-2000A 轨道电路模型及传输线理论,建立包含传输线与集总参数元件2 部分的节点导纳时域方程,利用拉普拉斯变换将时域方程变换到复频域,在复频域内直接考虑高频损耗,经变换解耦得到接收端轨面电压复频域解;最后,利用傅里叶变换结合Q-D 算法求得数值时域解,进而分析ZPW-2000A轨道电路暂态响应。
1 考虑高频损耗的轨道电路接收端轨面电压求解方法
1.1 轨道电路模型
ZPW-2000A 轨道电路由钢轨及补偿电容、调谐单元、空心线圈等集总参数元件构成。其中,补偿电容让传输通道趋于阻性,保证轨道电路具有良好的传输性能,增加信息在轨道电路上的传输距离;调谐单元和空心线圈构成电气绝缘节,实现相邻区段的电气隔离和信号传输[5]。根据轨道电路传输特性,将钢轨等效为均匀有损传输线[6],按照标准TB/T 3206—2017《ZPW-2000 轨道电路技术条件》,设定传输线总长度为1 km,建立轨道电路模型如图1 所示。图中:L1和L2为调谐单元的电感;C1,C2和C3为调谐单元的电容;R1,R2和R3为调谐单元的电阻[7];Rg和Lg分别为钢轨的电阻和电感;Rs和Ls分别为空心线圈的电阻和电感;Rt和Lt为钢轨引接线的电阻和电感;Cb为补偿电容,电路中只配置了2 个补偿电容,实际应用时配置的补偿电容数量一般大于2 个,因为多个补偿电容的建模方法和图1中类似,为了增加可读性进行省略;Rf为分路电阻;MTL 为多导体传输线(Multiconductor Transmission Line,MTL);l为MTL2 的长度;钢轨1 为信号源所加钢轨,则另一条钢轨为钢轨2。
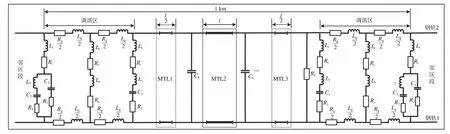
图1 轨道电路模型
图1 中,MTL 部分是由多个完整的单位长度等值电路构成,单位长度传输线等值电路如图2 所示。图中:Rnn,Lnn,Cnn(n=1,2)分别为第n根钢轨的单位长度自电阻、自电感、自电容;L12,C12分别为钢轨之间的互电感、互电容;G11,G22分别为对应钢轨与大地间的漏电导;G12为钢轨1与钢轨2 经由道砟和轨枕的道床电导,由道床电阻Rd表征,为1/Rd;z为节点距传输线始端距离;Δz为z的增量;t为时间;a为整数系数;Ii(z,t)为传输线上的电流,i=1,2;Vi(z,t)为传输线的对地电压[8]。
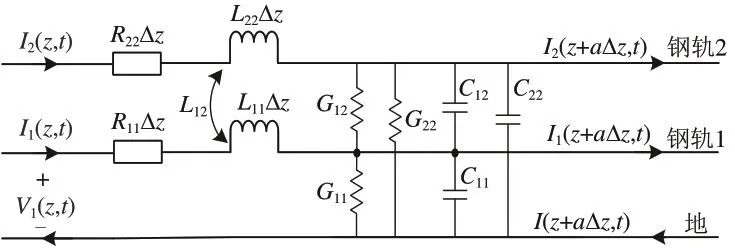
图2 单位长度传输线等值电路
根据轨道电路模型和节点导纳法,可得节点导纳时域方程为

式中:CM为由电容、电感决定的N×N型矩阵;N为由节点数决定的常数;P为MTL 的数量[9];nk为第k段MTL 的端口数;GM为由电阻决定的N×N型电导矩阵;IM(t)为由信号源决定的N×1 型电流矩阵;VM(t)为由节点电压和电感电流决定的N×1 型矩阵;Ik(t)为流入第k段传输线的nk×1型电流矩阵[10];Dk为MTL端口选择矩阵。
由于轨道电路模型中存在空心线圈、调谐单元等集总参数元件,不能直接利用时域有限差分法建立方程,需要将轨道电路模型分为传输线和集总参数元件2 部分,分别建立方程。而利用节点导纳法能够直接建立包含传输线部分和集总参数元件部分的节点导纳时域方程。
1.2 基于节点导纳方程的轨面电压复频域解
为方便计算高频损耗,将节点导纳时域方程转换到复频域内进行求解,避免了在时域内需要结合矢量匹配法对参数进行拟合以及极点、留数的复杂计算。
将式(1)进行拉普拉斯变换,且设为零初始条件,得到复频域方程为

其中,

式中:s为拉普拉斯算子;Ik,1(s)和Ik,2(s)分别为MTL输入端和输出端的电流矩阵。
由单位长度传输线等值电路及传输线理论,可得
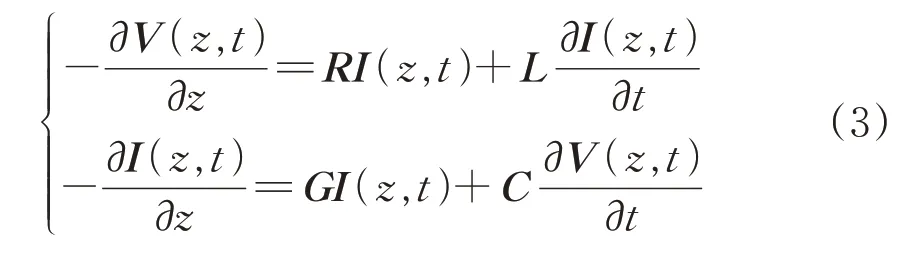
式中:R,L,G和C分别为单位长度MTL 的电阻、电感、电导和电容矩阵。
将式(3)转换为复频域形式,为
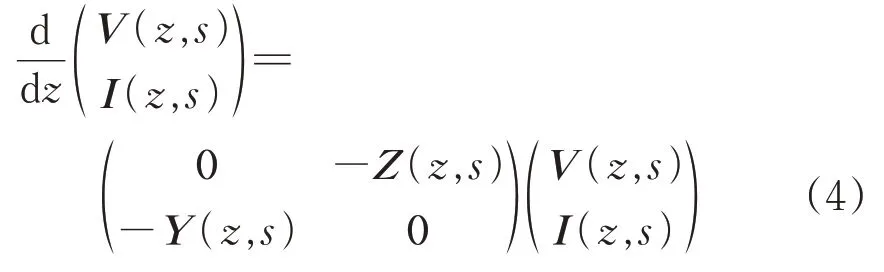
其中,
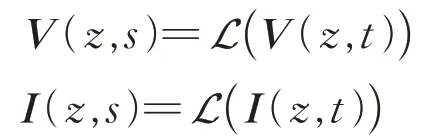
式中:V(z,s)和I(z,s)分别为对距离MTL 输入端z处电压和电流进行拉普拉斯变换得到的电压和电流矩阵;Z(s)和Y(s)分别为阻抗矩阵和导纳矩阵[11]。
MTL 损耗表现为导体损耗和周围介质损耗,一般情况下这些损耗都与频率有关,且高频时会产生额外的高频损耗。高频损耗主要由导体中的集肤效应和电介质中的极化现象引起的,而极化损耗对MTL 影响甚微,可以忽略不计[12]。因此,考虑集肤效应损耗,将阻抗矩阵Z(s)表示为
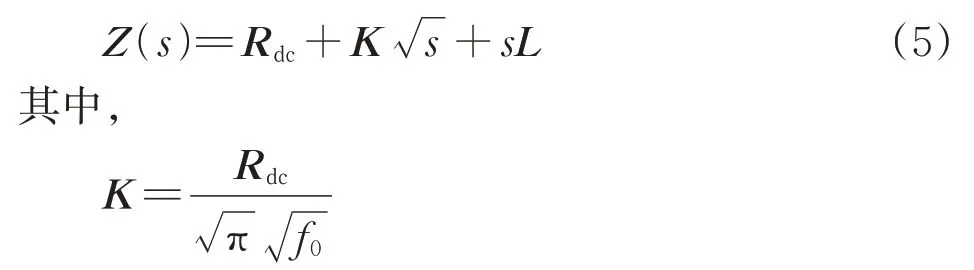
式中:Rdc为直流电阻矩阵;f0为转折频率;K为高频损耗。
为方便计算,将式(4)写为紧凑矩阵形式为
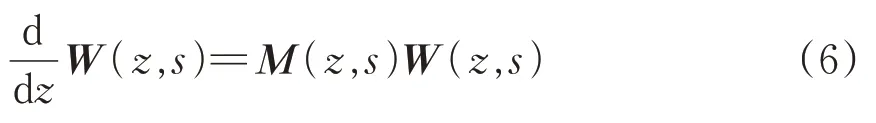
传输线输入端与输出端的紧凑矩阵关系为
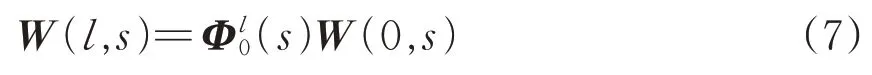
其中,
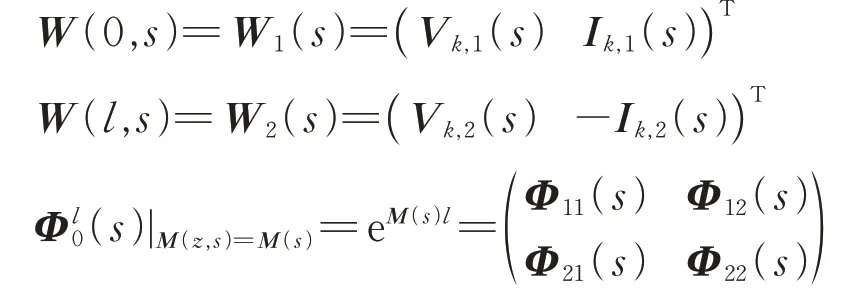
式中:W(0,s)和W(l,s)分别为距传输线始端z=0和z=l处的矩阵;(s)为积分矩阵。
根据上述计算式,可得
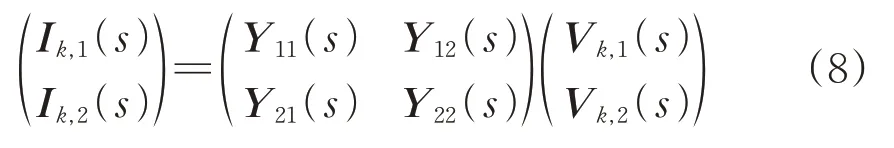
其中,
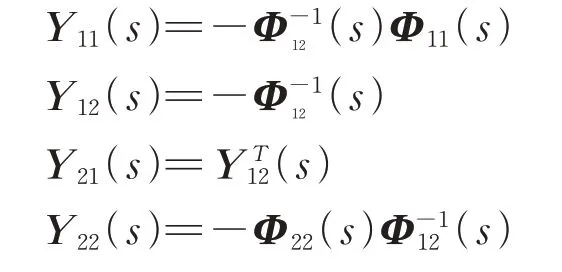
根据上式可知Ik(s)=Yk(s)Vk(s);再将其代入式(2),求得节点导纳复频域方程为

1.3 基于傅里叶变换结合Q-D 算法的轨面电压时域解
针对式(9),利用傅里叶变换结合Q-D 算法可求得VM中包含的节点电压时域解,再进行暂态响应分析,并根据拉普拉斯基本定义式,可得
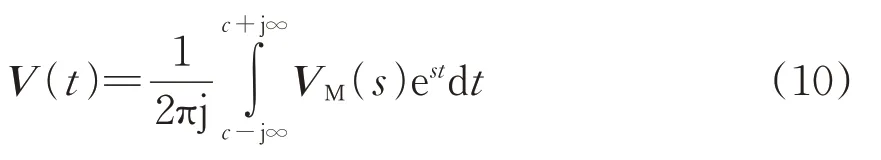
式中:c为收敛横坐标。
将式(10)进行离散化,再划分积分域后得到表达式[13]为
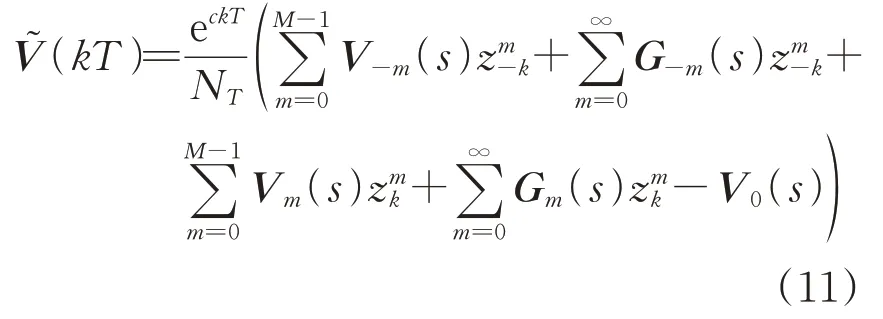
其中,

式中:T为周期;K为由离散点决定的正整数;Er为设定的相对误差;NT为常数;α为函数的指数阶数。
式(11)等号右侧括号中第1 项和第3 项分别由快速傅里叶变换和快速傅里叶逆变换算法进行求解;而第2 项和第4 项为无限求和项,因此用连分式近似代替无穷幂级数的和[14],即为

式中:P取正整数;dn(n=0,1,…,2P)为连分式各项系数。
式(12)中dn(n=0,…2P)可用Q-D菱图进行求解,其算法如图3所示。

图3 Q-D菱图
图3中,前2列元素的计算式为

其余列元素的计算式为
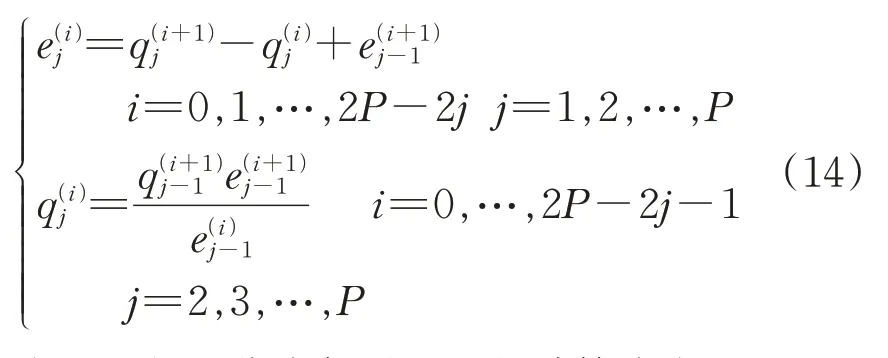
由此可得连分式各项系dn的计算式为
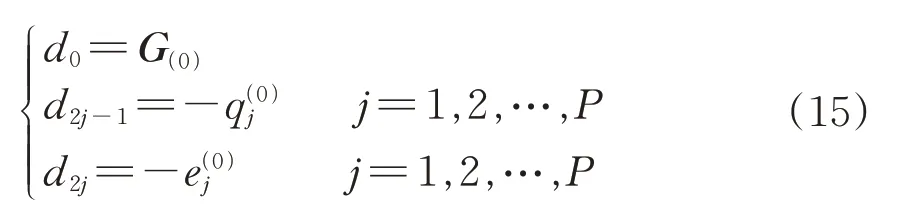
2 方法验证
ZPW-2000A 轨道电路的载频频率为1 700,2 000,2 300 和2 600 Hz,调谐区的引接线参数见表1,传输线参数参见文献[16]。
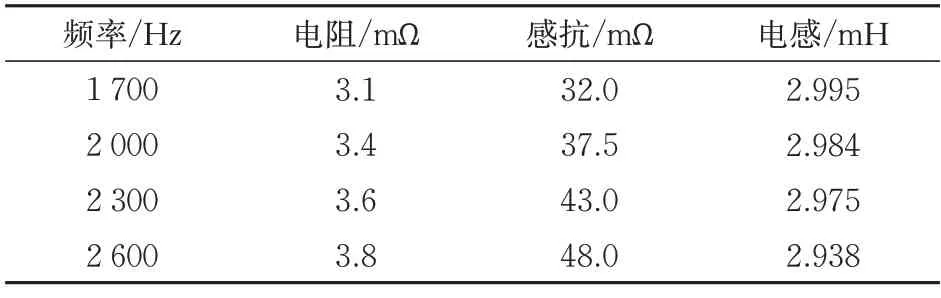
表1 引接线参数
轨道电路发送端和接收端的调谐区参数相同[17],1 700~2 300 Hz 载频轨道电路调谐单元BA1和BA2的参数见表2。

表2 调谐单元参数
选取钢轨类型为60 kg·m-1,信号源电压Vs(t)=sin2(ωt),其 中ω=2 πf,假定频率f=1 700 Hz,Rg=0.021 Ω,Lg=18.2 μH,Rs=0.03 Ω,Ls=33 μH,Cb=55 μF,运用时域有限差分法与本文方法进行比较,计算结果如图4所示。
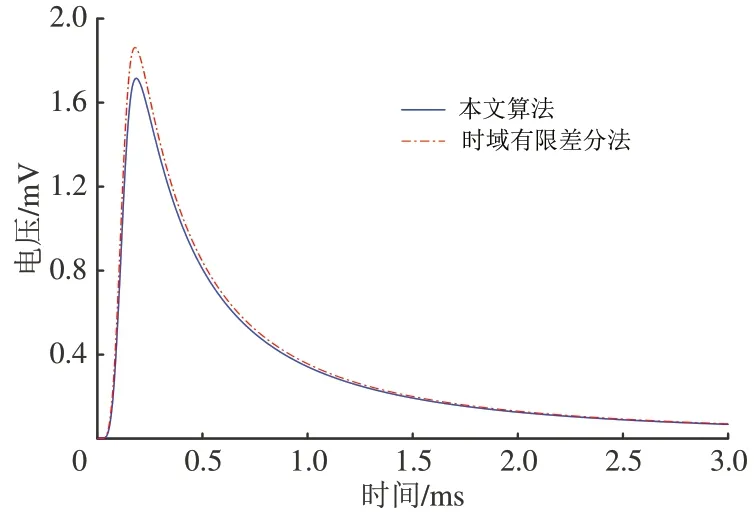
图4 接收端轨面电压暂态响应
由图4 可知,将本文方法与时域有限差分法求解的结果进行对比,误差在8%以内,具有较高的计算精度,验证了本文方法的正确性。
同等条件下,利用时域有限差分法和本文方法计算轨道电路接收端轨面电压,耗时分别为368 和117 s。
因此,利用本文方法将集总参数元件及高频损耗在复频域内进行处理,避免了时域内的卷积计算和迭代计算,计算时长仅约为时域有限差分法的32%。
3 暂态响应分析结果
3.1 MTL沿线轨面电压
钢轨1 与钢轨2 上MTL 沿线电压的计算过程相同,因此,在考虑高频损耗时,只计算了钢轨1上MTL的沿线电压,结果如图5所示。
由图5 可知,利用本文方法可得到沿线电压的暂态响应三维图,不仅能反映时间上的沿线电压响应,还能反映空间距离上的沿线电压变化。
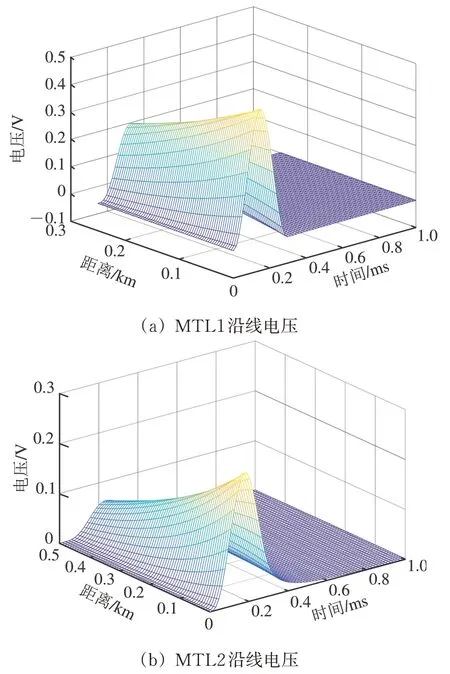
图5 钢轨1沿线电压
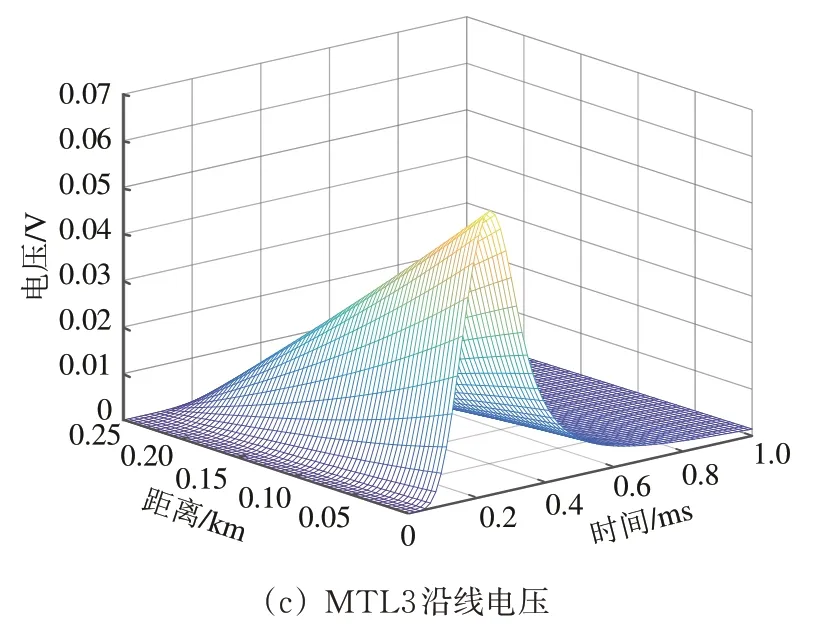
图5 钢轨1沿线电压
3.2 影响因素对暂态响应的影响
3.2.1 高频损耗
考虑高频损耗时,阻抗计算式为式(5);未考虑高频损耗时,式(5)中表示高频损耗项“K”为0。基于以上分析方法,选取频率为1 700 Hz,将对应的阻抗分别代入后续的计算,得到考虑高频损耗与否的接收端轨面电压暂态响应如图6所示。
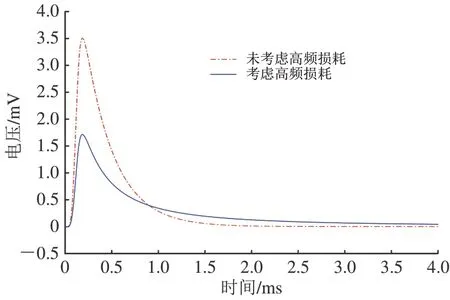
图6 不同高频损耗下接收端轨面电压暂态响应
由图6 可知,考虑高频损耗的轨道电路接收端轨面电压的幅值小于未考虑高频损耗时得到的轨面电压幅值,符合有损传输线规律[18]。
3.2.2 频率
ZPW-2000A 轨道电路的载频信号频率为1 700,2 000,2 300 和2 600 Hz,因此将其作为计算频率进行分析,得到不同频率下的接收端轨面电压暂态响应如图7所示。

图7 不同频率下接收端轨面电压暂态响应
由图7 可知,频率越大,接收端轨面电压幅值越小。随着信号频率增大,钢轨和大地的集肤效应就越强,高频损耗也就越明显,电压幅值也就越小,图7呈现的结果符合这一规律[19]。
3.2.3 分路电阻
当轨道电路表面生锈或积污时,分路电阻过高致使轨道电路分路不良[20],得到不同分路电阻下接收端轨面电压与分路电阻的关系如图8所示。

图8 不同分路电阻下接收端轨面电压暂态响应
由图8 可知:随着分路电阻增大,接收端轨面电压降越来越小,小到一定值时可能导致轨道电路出现分路不良的情况;在列车驶入和出清时,无论分路电阻如何变化,暂态过程依然存在。
3.2.4 调谐区状态
将调谐区设置为故障状态,对比正常状态时接收端的轨面电压暂态响应,结果如图9所示。
由图9 可知,当调谐区故障时,接收端轨面电压暂态响应与正常状态时的暂态响应有所区别,为轨道电路的故障诊断提供一定的参考[21]。

图9 不同调谐区状态下接收端轨面电压暂态响应
3.2.5 道床电阻
道床电阻在外界环境中易受温度和湿度的影响,其作为一次侧参数会影响信号在钢轨上的传输,因此,为研究道床电阻对轨道电路接收端轨面电压的影响规律,得到不同道床电阻下轨面电压暂态响应如图10所示。
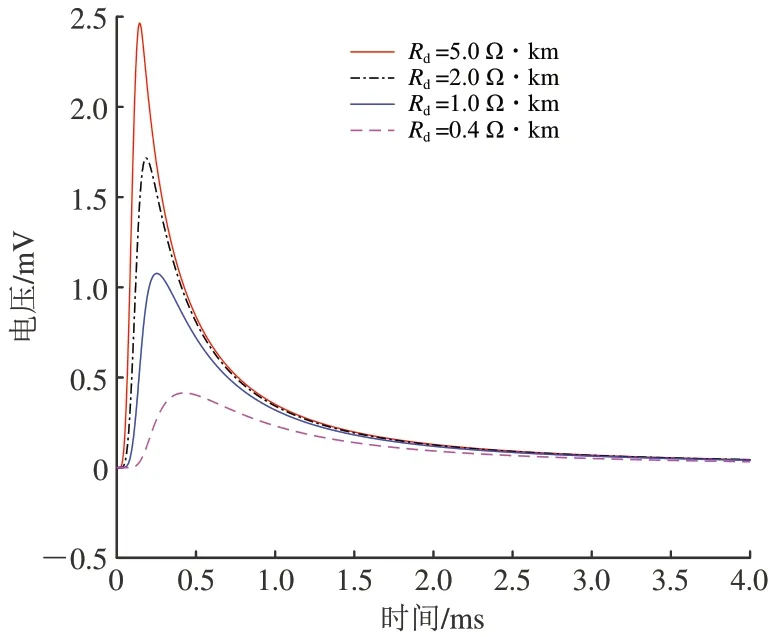
图10 不同道床电阻下轨面电压暂态响应
由图10 可知,在其他参数不变的情况下,随着道床电阻的减小,信号在传输过程中的漏泄电流增大,接收端轨面电压的幅值也随之减小,且当道床电阻过小时,可能出现“红光带”故障情况[22]。
4 结论
(1)针对ZPW-2000A 轨道电路中因高频损耗影响而难以准确分析暂态响应的问题,提出在复频域内直接将高频损耗项纳入阻抗计算式进行计算,避免了时域有限差分法的复杂计算。
(2)通过分析ZPW-2000A 轨道电路暂态响应,可知考虑高频损耗的轨道电路接收端轨面电压小于未考虑高频损耗时的电压幅值。在列车驶入和出清时,接收端信号均出现暂态变化,且接收端轨面电压降随着分路电阻的增大而减小,随着道床电阻的增大而增大,但是分路电阻过高可能导致分路不良情况,道床电阻过小可能导致“红光带”故障情况。
(3)与利用时域有限差分法的计算结果进行对比,求解方法误差在8%以内,且计算耗时短;该方法可以准确、高效地分析高频损耗下ZPW-2000A轨道电路暂态响应,为轨道电路暂态响应的分析提供理论参考。
