基于块体离散单元法的走滑型活动断裂错动作用下隧道结构响应

许学良，马伟斌，金爱兵，柴金飞，罗金涛

（1.中国铁道科学研究院集团有限公司 铁道建筑研究所，北京 100081；2.高速铁路轨道技术国家重点实验室，北京 100081；3.北京科技大学 土木与资源工程学院，北京 100083）

受限于线路走向和地形地质条件，长线型的隧道结构不可避免地穿越活动断裂带［1-2］。近年来，穿越活动断裂带隧道结构的抗错和抗震问题越来越受到国内外工程界重视，并成为地下工程研究的难点和热点问题之一［3］。历次震害统计结果表明，断裂错动是造成隧道结构变形破坏的最主要因素［4-8］。

在隧道穿越活动断裂带对策上，当前主要的设计规范［9-10］给出的多为原则性规定和建议，缺乏对隧道结构的具体性要求。既有穿越活动断裂带隧道工程措施主要有“铰链设计”“隔离消能设计”和“超挖设计”等［11］，关于前2 种工程措施的研究相对较多［1-2，12-13］，一些学者得出了有益结论；关于“超挖设计”的研究则相对较少。超挖设计可分为改变隧道断面型式和扩挖断面，对于前者，考虑到圆形隧道的断面受力较好，因此穿越活动断裂带隧道多采用圆形或类圆形断面型式；对于后者，扩挖断面的具体数值即预留位错空间，通常根据活动断裂错动方式及错动量确定，并多依靠经验给出。如：美国旧金山湾区捷运系统BART的Berke⁃ley 隧道在穿越Hayward 活动断裂带时采用圆形断面，断面扩挖1英尺（约30 cm），而穿越同一断裂带的旧金山Claremont 输水隧洞［14］在侧洞外缘到主洞衬砌内缘处预留2.6 m 位错空间；我国兰新铁路乌鞘岭隧道穿越F7活动断层时［15］采用了预留百年的位错空间（水平25 cm，垂直5 cm）；我国大瑞铁路高黎贡山隧道穿越镇安及勐冒活动断裂时，隧道断面预留35 cm位错空间［16］。

在穿越活动断裂带隧道结构的错断破坏机理研究上，常用的研究手段为室内模型试验和数值仿真试验。模型试验比例尺一般较小，多为1∶50～1∶30［12-13，17］，具有缩尺效应，而且结果离散性大、重复性差。随着计算机性能的提升，数值仿真试验得到广泛应用。已有学者在研究跨断层隧道结构响应机理时采用了以ABAQUS 和FLAC 为代表的有限元分析方法［18-20］，该方法计算效率高，适用于连续介质大变形工况，但无法真实再现隧道衬砌结构与围岩及断层之间错动损伤破坏过程。相比有限元法，离散单元法克服了连续介质的宏观连续性假设，在模拟分析局部破裂上优势明显［21］。马亚丽娜等［22］采用三维离散-连续耦合方法分析了跨正断层隧洞因错动而产生的位移变化及力学响应，为香炉山隧洞抗断措施设计提供了指导。但目前尚未有采用离散单元法分析走滑型活动断裂错动作用下隧道结构响应的研究报道。

在隧道纵向破坏范围的划分和断面环向损伤破坏指标的具体量值上，目前业界缺乏统一的控制标准。对于隧道纵向上的影响范围，多采取定性的估算方式［18，20］。对于隧道横断面上的损伤，王鸿儒等［23］利用ABAQUS中混凝土本构的受拉损伤因子和受压损伤因子来判定隧道截面的损伤破坏程度；唐浪洲等［24］采用最大剪应变0.002 判断衬砌是否发生破坏；城市地铁领域中，相关标准规范［25-26］分别以层间位移角1 250 和直径变形率6‰作为评价城市地铁隧道矩形和圆形断面损伤状态的具体指标。

以某穿越走滑型活动断裂带隧道为工程背景，首先采用离散单元法建立围岩-衬砌-断裂带三维块体离散单元模型，分析不同错动量作用下隧道衬砌整体位移响应；然后明确统一的结构位移及断面变形损伤控制标准，以预留位错空间30 cm 的方案为例，分析走滑型活动断裂错动作用下隧道纵向上的位移变化和横断面上的径向变形损伤规律，对比30，60 和90 cm 这3 种断面预留位错空间方案下隧道衬砌响应规律，结果可为隧道抗错设计及施工提供借鉴指导。

1 工程概况及数值模型

1.1 工程概况

工程背景为某单洞双线隧道，隧道长度超过20 km，最大埋深约1 200 m。隧址区地质构造复杂，区域深大断裂发育，近场区强震活动水平较高，地震活动分布不均匀，明显受多条区域性活动断裂控制。其中，YLX 断裂带与隧道轴向呈约76°大角度相交，相交处隧道埋深约340 m，断裂带宽约118 m，断裂带距离隧道出口约6.8 km。根据现场勘探资料，YLX 断裂带为左旋走滑型，黏滑运动，水平错动速率为3～4 mm·a-1，发震能力可能在6～7 级。以邻近发生的2010 年玉树7.1 级地震最大错动量［27］作为参考，YLX 断裂带未来最大突发错动量不超过1.8 m。

选取穿越YLX 断裂带及其两侧一定范围的隧道区段为研究对象。断裂带内为Ⅵ级软弱破碎围岩，断裂带外为Ⅴ级围岩，隧道区段采用Ⅵ级围岩复合式衬砌。受限于当前的技术条件，隧道埋深处错动量尚无法确定，综合当前技术条件和工程经济合理性，设计3种断面预留位错空间方案，分别为30，60 和90 cm。不同预留位错空间下隧道衬砌支护参数均相同，其中初期支护为C30 喷射混凝土，厚度25 cm；二次衬砌结构为C35 钢筋混凝土，厚度60 cm。以预留位错空间30 cm 方案为例，此时隧道净空断面高×宽为11.68 m×12.65 m，如图1所示。

图1 穿越活动断裂隧道典型断面（预留位错空间30 cm）（单位：cm）

1.2 模型建立

1）模型及隧道结构尺寸确定

采用离散单元法，建立围岩-衬砌-断裂带三维块体离散单元模型如图2 所示。综合设计资料、相关规范［10］及计算效率等因素，确定参数：模型尺寸为160 m×80 m×80 m（长×宽×高），宽度和高度方向上模型边界至隧道中心取3D，D为隧道跨度；隧道设置于模型中间，断面净空尺寸高11.68 m，跨度12.65 m；断裂带宽20 m，离散为5条间距5 m 的断裂，倾角为90°，与隧道轴线夹角为76°；衬砌节段长9 m、共18 个，变形缝宽0.1 m、共17 条；计算时对隧道衬砌单元网格加密，生成的模型共计7 792个块体、555 314个单元。2）材料参数赋值围岩、断裂带及衬砌材料采用Mohr-Coulomb本构模型，具体参数见表1。其中：围岩和断裂带分别根据文献［28］中的Ⅴ级和Ⅵ级围岩物理力学参数取值；初期支护、二次衬砌和变形缝单元根据文献［29］取值。模型中各接触面采用Mohr-Coulomb 弹塑性本构模型，力学参数根据文献

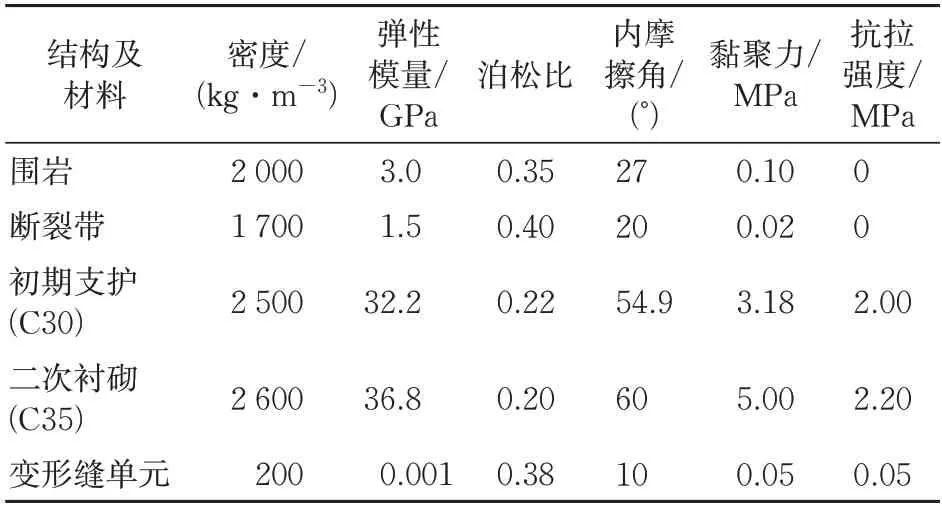
表1 围岩、断裂带及衬砌材料参数

图2 围岩-衬砌-断裂带三维块体离散元模型

［30］和文献［18］综合确定，具体见表2。

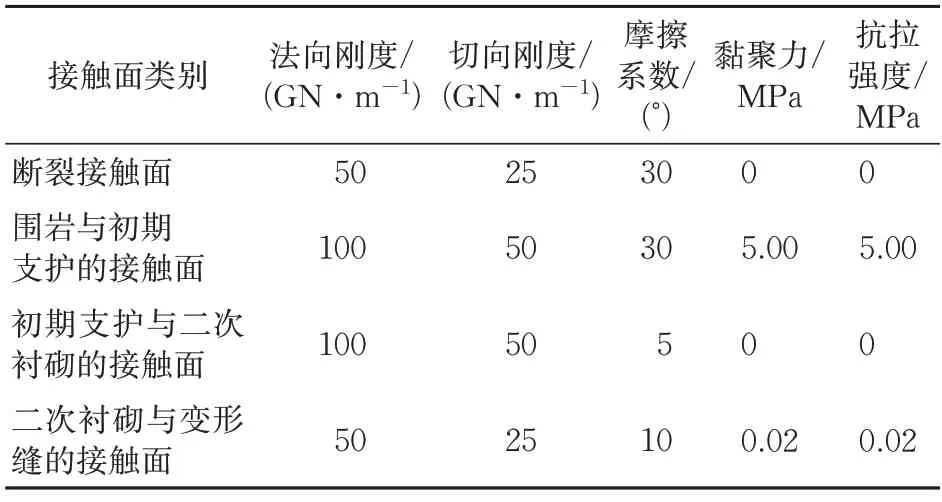
表2 接触面计算力学参数

3）边界条件设置

设置2 类边界条件：①速度边界条件，设置模型底部、模型前后左右四周的边界节点法向速度为零；②应力边界条件，根据实际在模型顶部施加垂直向下的应力，应力值等于上覆岩层自重，取为8.51 MPa。

4）地应力平衡

采用水压致裂法获得隧址区40 组地应力数据，通过回归分析可知，在埋深不超过400 m 时，侧压力系数比值约为2.25（σH和σv分别为最大水平主应力和垂直主应力），侧压力系数比值约为1.35（σh为最小水平主应力）。据此，隧道区段埋深处的垂直主应力取9 MPa，最大水平主应力取20.25 MPa，最小水平主应力取12.15 MPa。

为防止模型在施加地应力时出现屈服开裂，先对模型进行弹性状态下地应力平衡求解，然后赋予实际材料参数计算至平衡，结果如图3 所示。图中：正、负值分别表示拉、压应力。由图3 可知：断裂带周围应力场波动变化较大，断裂带处的垂直主应力和最小水平主应力明显高于断裂带两侧的，其分布呈“W”形，这可能与断裂带两侧地层围岩构造运动及挤压有关；与隧道轴线平行的最大水平主应力在断裂带处波动较缓。

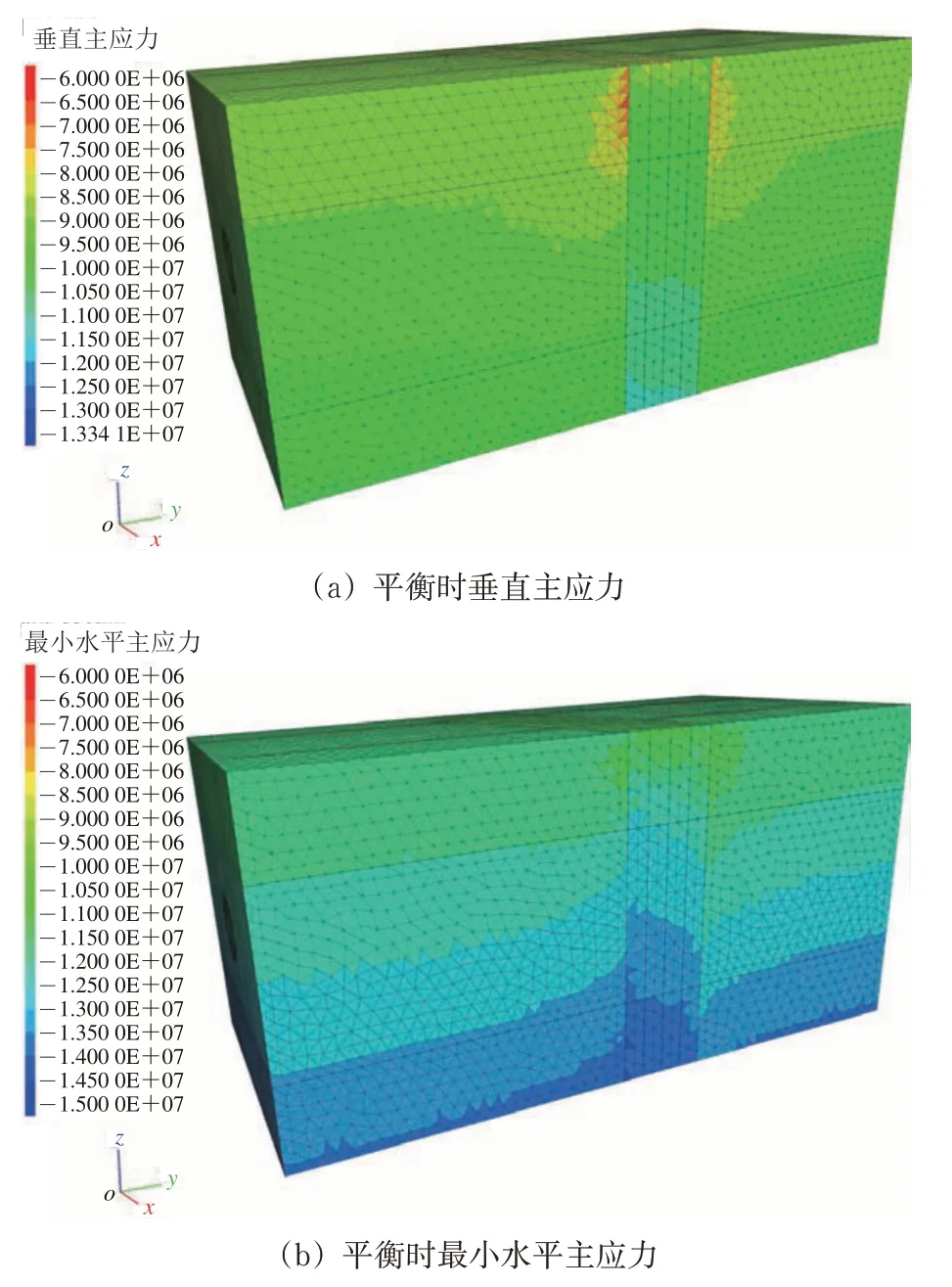
图3 模型地应力平衡结果

5）开挖支护平衡

为聚焦断裂错动，暂不考虑隧道开挖后对衬砌支护结构的影响，计算时直接一次性开挖，然后施加初期支护、二次衬砌和变形缝等隧道衬砌结构；开挖支护平衡后，模型位移清零，并将其作为后续开展走滑错动研究的基础模型。

1.3 模型验证

得到离散单元模型后，分别采用室内模型试验和震害调研2 种形式，对隧道衬砌结构纵向扭转形态和衬砌节段间错台开展趋势验证。

在走滑型断裂错动作用下，文献［18］的室内缩尺模型最终形态及本文所用的数值模型计算结果如图4 所示。图中：数字表示缩尺模型的衬砌节段编号。由图4 可知：模型试验中，主动侧和固定侧的隧道衬砌在断裂带附近发生扭转、偏移，纵向上呈“S”形；本文所用的数值模型计算结果与室内缩尺模型试验最终形态趋势总体一致，隧道衬砌水平位移亦呈“S”形，显著性差异错动位移主要集中在断裂带及其两侧附近。

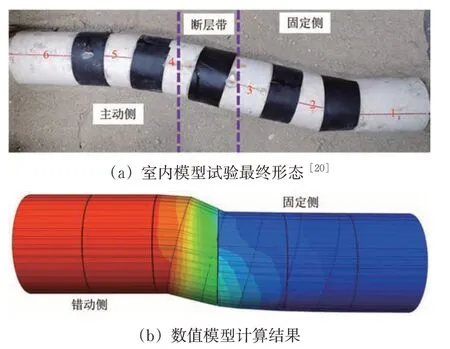
图4 走滑型断裂错动作用下隧道衬砌纵向最终形态

结合文献［12］对汶川地震中龙溪隧道的震害调研成果，进行衬砌节段间错台的趋势印证，如图5 所示。由图5 可知：此次地震虽然为逆断层运动诱发的区域地震，但引起隧道所穿越的次级断裂却表现出走滑特征［13］，造成衬砌节段施工缝处出现较大错台；本研究所用的数值模型计算结果中断裂带范围内隧道衬砌节段间表现出明显的错台，与龙溪隧道震害调研结果趋势一致，且错台量随着断裂错动量的增加而增大。

图5 走滑型断裂错动作用下隧道衬砌错台

室内模型试验和震害调研均表明，本文建立的三维块体离散元模型能较为真实地反映走滑型断裂错动作用下隧道衬砌结构的响应特征。

2 监测断面分布及错动位移场

2.1 监测断面及监测点

块体离散单元模型的应力应变离散性较大且无明显规律，因此以隧道断面上关键节点的位移作为监测变量。设置监测断面共计30 个，在断裂带附近进行加密，每个衬砌节段的两端都设有监测断面；在远离断裂带处，每个衬砌节段只监测1个断面。沿隧道纵向监测断面分布如图5 所示。图中：隧道中心线附近数字表示衬砌节段编号；以断裂带中心为界，红色和蓝色虚线分别表示左侧和右侧的监测断面；监测断面编号记为“衬砌节段编号-断面序号”，如“22-1”表示编号22 的衬砌节段的第1 个监测断面。各监测断面上测点布置一致，如图6 所示。图中：红色圆点为监测点，分布在拱顶、左右拱腰、左右拱脚、左右墙脚、仰拱底部，共8处。分别取拱顶—仰拱底部、左拱脚—右拱脚、左拱腰—右墙脚和右拱腰—左墙脚的测点间相对位移，用于隧道横断面径向变形损伤评估。

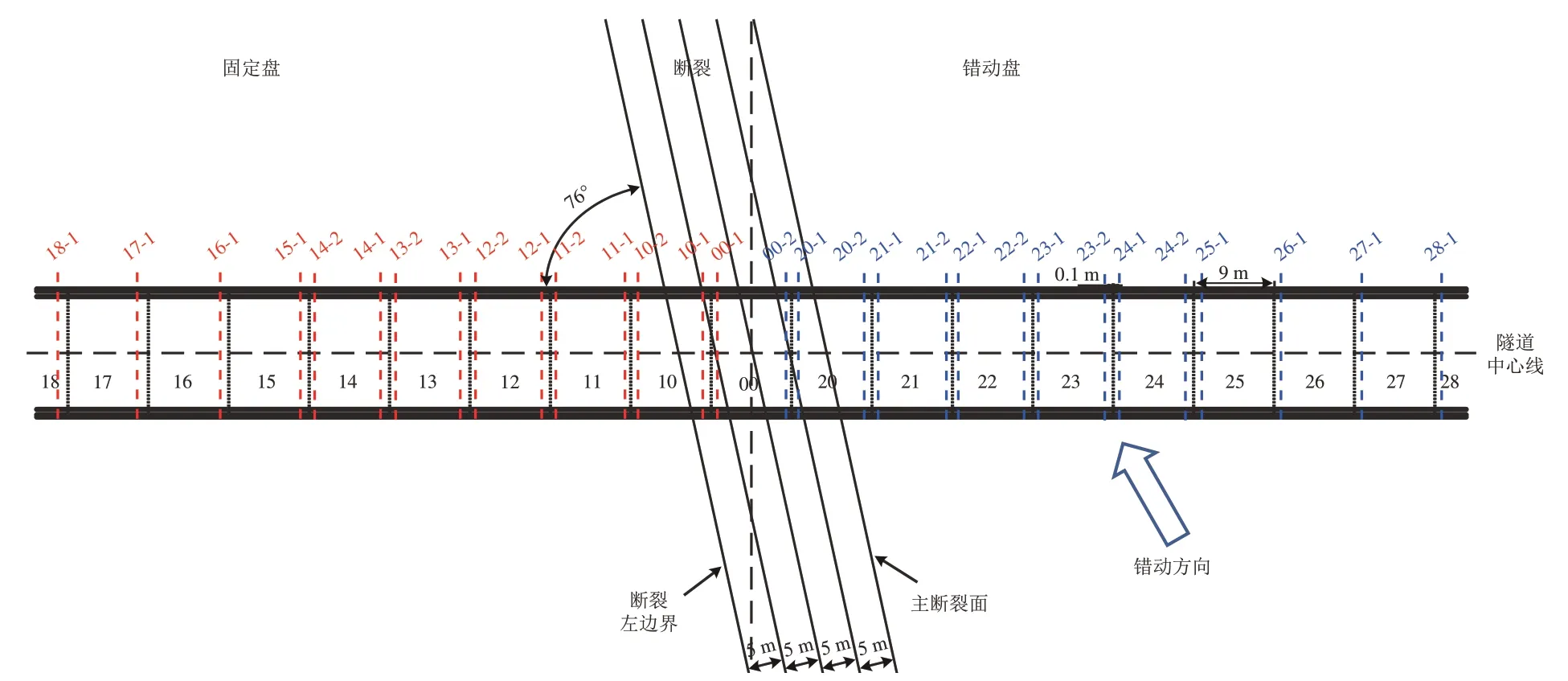
图6 沿隧道纵向监测断面分布图

图7 监测断面上监测点布置示意图

2.2 错动位移场

将基础模型的固定盘底部固定，对错动盘施加水平向速度，沿主断裂面走向，分别按错动0.05，0.10，0.15，0.20，0.25，0.30，0.35，0.40，0.45，0.50，1.00，1.50 和1.80 m 共计13 种工况计算隧道衬砌位移响应。

图8 展示了部分错动量下隧道衬砌整体位移云图。由图8 可知：受断裂错动产生的挤压、剪切、张拉等作用影响，即使水平错动量较小，主断裂面附近两侧衬砌依然发生明显的位移变化；随着断裂错动量的增加，断裂两侧衬砌整体位移差异越来越显著，影响范围越来越大，在远离断裂的隧道两端，由于衬砌自身的刚性约束作用，差异较小，衬砌整体稳定。

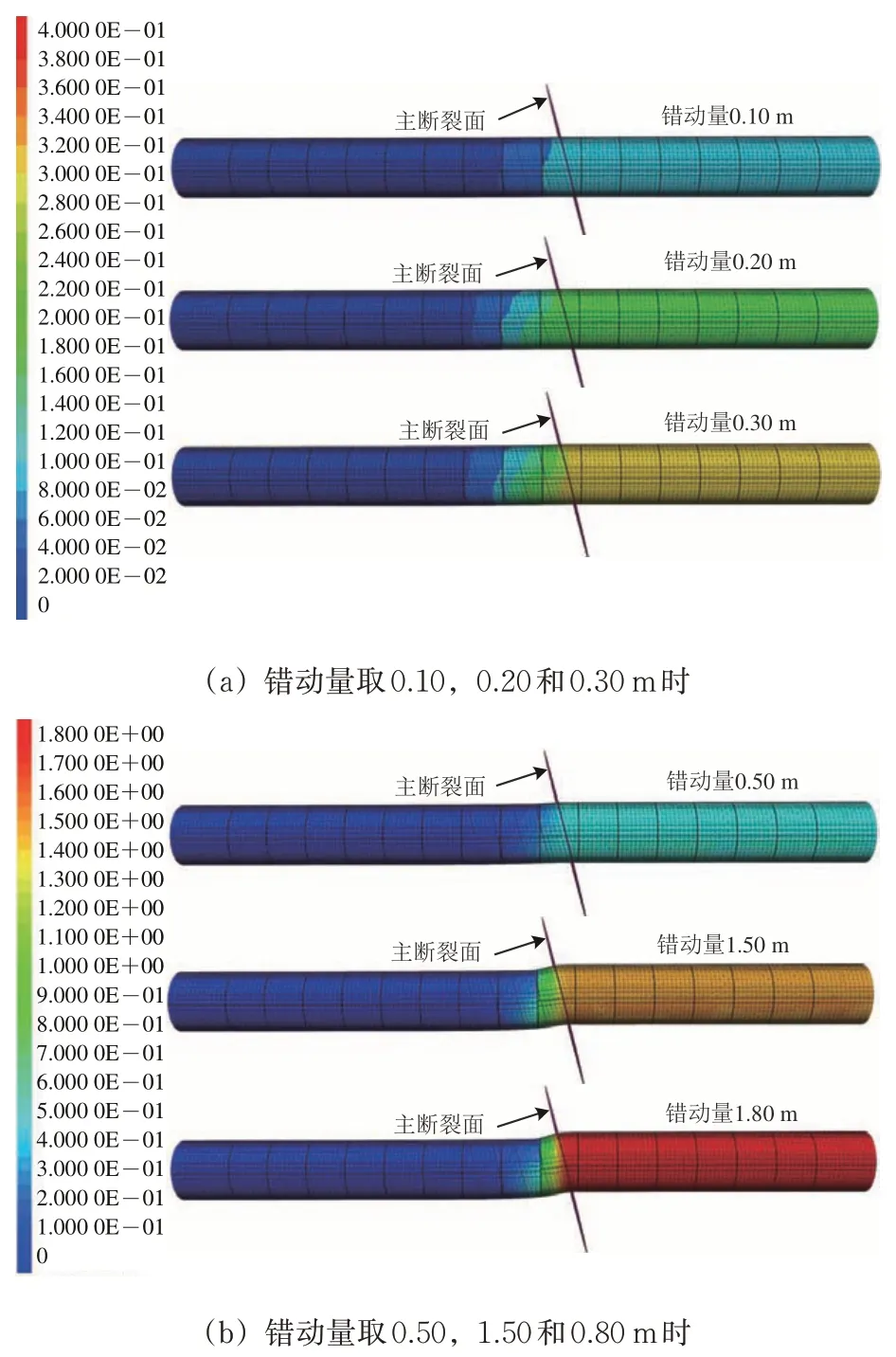
图8 不同走滑错动量下隧道衬砌整体位移（部分）

为清晰展示断裂带处隧道衬砌在走滑错动下的竖向位移，以错动量最大（1.8 m）工况为例，给出此时衬砌竖向位移局部剖视图，如图9 所示。图中：正值表示位移竖直向上，负值表示位移竖直向下。由图9 可知：较大的竖向位移集中在主断裂面所横跨衬砌的变形缝附近，衬砌拱顶下沉，最大沉降量为432.7 mm，仰拱上拱，最大上拱量为557.1 mm；另外，断裂带附近发生衬砌剥落掉块、隧底隆起分离，体现了离散单元法能够再现局部破裂分离的优势。

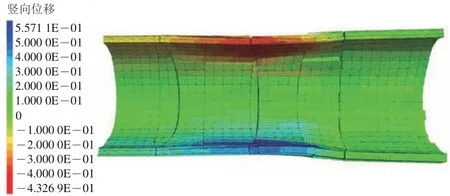
图9 断裂带处衬砌竖向位移剖视图（走滑错动1.8 m时）

3 走滑型活动断裂错动作用下隧道结构响应

在统一结构位移及断面变形损伤控制标准的基础上，以预留位错空间30 cm 的方案为例，分析隧道纵向上位移变化和横断面上径向变形损伤规律，并对比30，60 和90 cm 这3 种预留位错空间方案下的衬砌响应规律。

3.1 结构位移及类圆形断面变形损伤控制标准

断裂错动会引起隧道衬砌结构纵向上差异位移和横断面上径向变形，为此须统一结构位移和变形损伤控制标准，以确定影响范围和损伤破坏状态。

在隧道纵向上，衬砌节段之间因断裂错动而产生差异位移。根据《WJ-7 和WJ-8 特殊调整扣件暂行技术条件》（铁总科技［2015］16 号），轨道高低位置调整量为-10～60 mm。由于隧底与其上方轨道之间存在弹条垫板、轨道板等结构物，隧底与钢轨之间变形尚无确定关系。结合现场实际情况，采用±10 mm作为衬砌节段间相对差异位移的控制指标（正值表示上升或与错动方向一致，负值表示下沉或与错动方向相反），即差异位移的绝对值大于10 mm 时判定为不均匀变形区；反之判定为相对稳定区。

在隧道横断面上，开挖支护平衡后模型位移清零，仅考虑地层错动对隧道衬砌横断面变形影响，并通过隧道衬砌上监测点之间相对位移计算断面的变形率。复合式衬砌结构的变形损伤判定指标缺少相关研究。文献［25—26］给出的结构损伤椭圆率（隧道变形小于6‰）适用于城市地铁管片圆形隧道断面。穿越活动断裂带双线隧道断面型式为类圆形，可借鉴上述规范，取径向变形率Φ作为隧道结构变形损伤状态判定指标，定义为衬砌相对位置变形与对应的衬砌内径的比值，上下限取±6‰（正值表示径向张拉，负值表示径向压缩）。

3.2 隧道纵向上位移变化

隧道纵向上位移变化以拱顶和仰拱底部的竖向位移、左拱脚和右拱脚的水平位移为主；左、右拱腰和对向墙脚的竖向及水平位移变化与之相似，不做赘述。

1）拱顶竖向位移

不同错动量下，各衬砌节段拱顶的竖向位移及相邻衬砌节段间的差异位移如图10 所示。图中：隧道纵向位置取0为断裂带中心处，正、负值分别表示断裂带的右、左侧。由图10可得到如下结论。

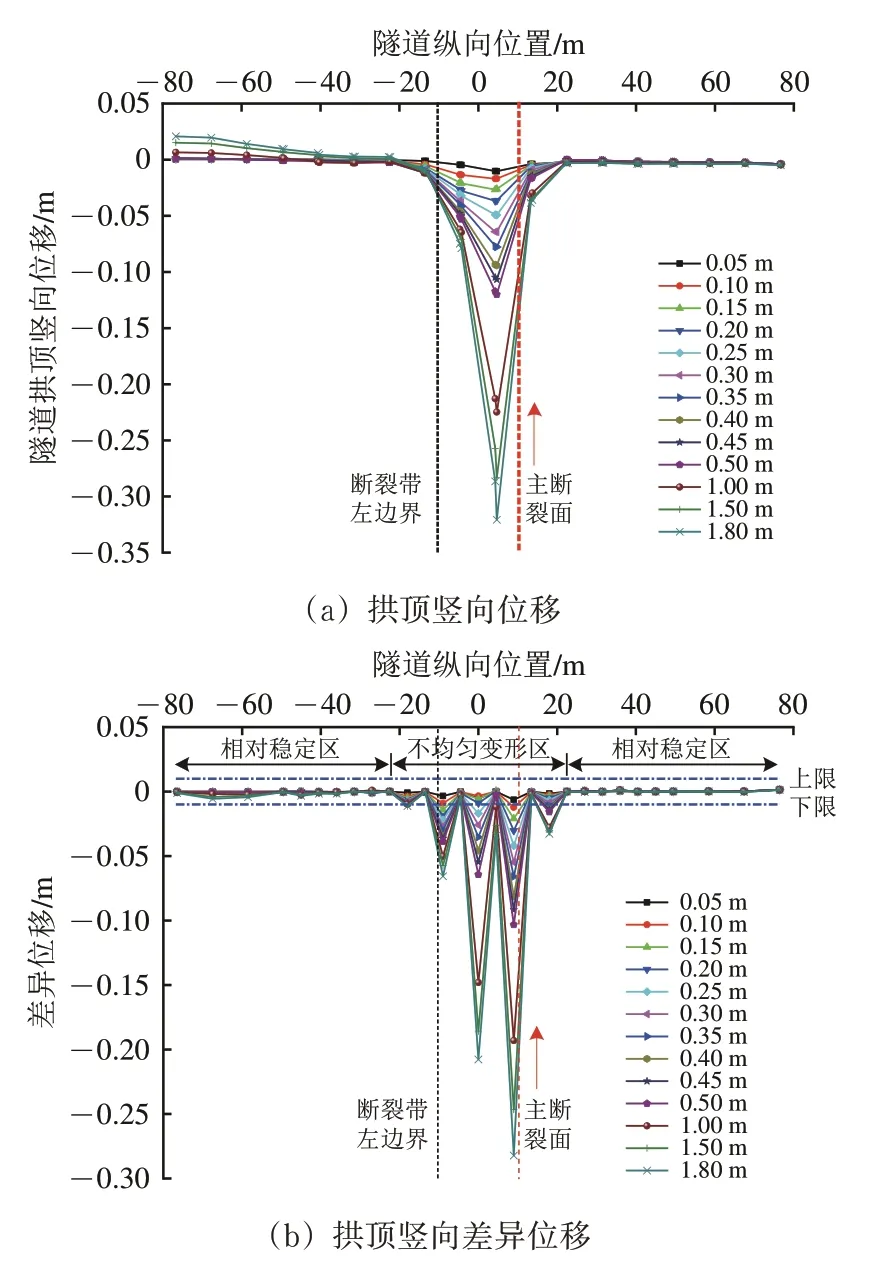
图10 拱顶竖向位移及差异位移（预留位错空间30 cm）

（1）受错动盘地层错动产生的挤压、剪切、张拉等作用，隧道拱部较大竖向位移主要集中在断裂带及其两侧附近，呈“V”形。随着错动盘错动量不断增加，主断裂面附近两侧隧道衬砌拱顶竖向位移越来越大，如错动量为0.1 m 时拱顶沉降的最大值为17.0 mm，错动量为1.8 m 时的最大值为320.7 mm，达到前者的18.8倍。

（2）距离断裂带越远，两端衬砌节段间拱顶竖向差异位移越小。在错动盘一侧，拱顶竖向位移均为负值，表明错动盘侧衬砌拱顶均下沉，其位移先增大后趋于稳定，约为5 mm；在固定盘一侧，拱顶竖向位移先急剧增大，后增速变缓、趋于平稳，错动量小于1.0 m 时该侧隧道衬砌拱顶竖向位移较小且基本不变，在1.2 mm 上下波动，而错动量不小于1.0 m 后，该侧与主断面距离大于20 m的隧道衬砌拱顶位移在不断增大，呈上翘趋势，这可能与衬砌挤压有关。

（3）不同错动量下，竖向位移的显著性差异主要集中在断裂带及其两侧附近，差异位移极值为282.3 mm，位于主断裂面附近。错动量大于0.50 m 后，显著性差异范围基本不变。以±10 mm 作为控制标准，不均匀变形区为固定盘侧距断裂带左边界12.2 m 至错动盘侧距主断裂面12.2 m 范围内，其余为相对稳定区。

2）仰拱底部竖向位移

不同错动量下，各衬砌节段仰拱底部的竖向位移及相邻衬砌节段间的差异位移如图11 所示。由图11可得到如下结论。

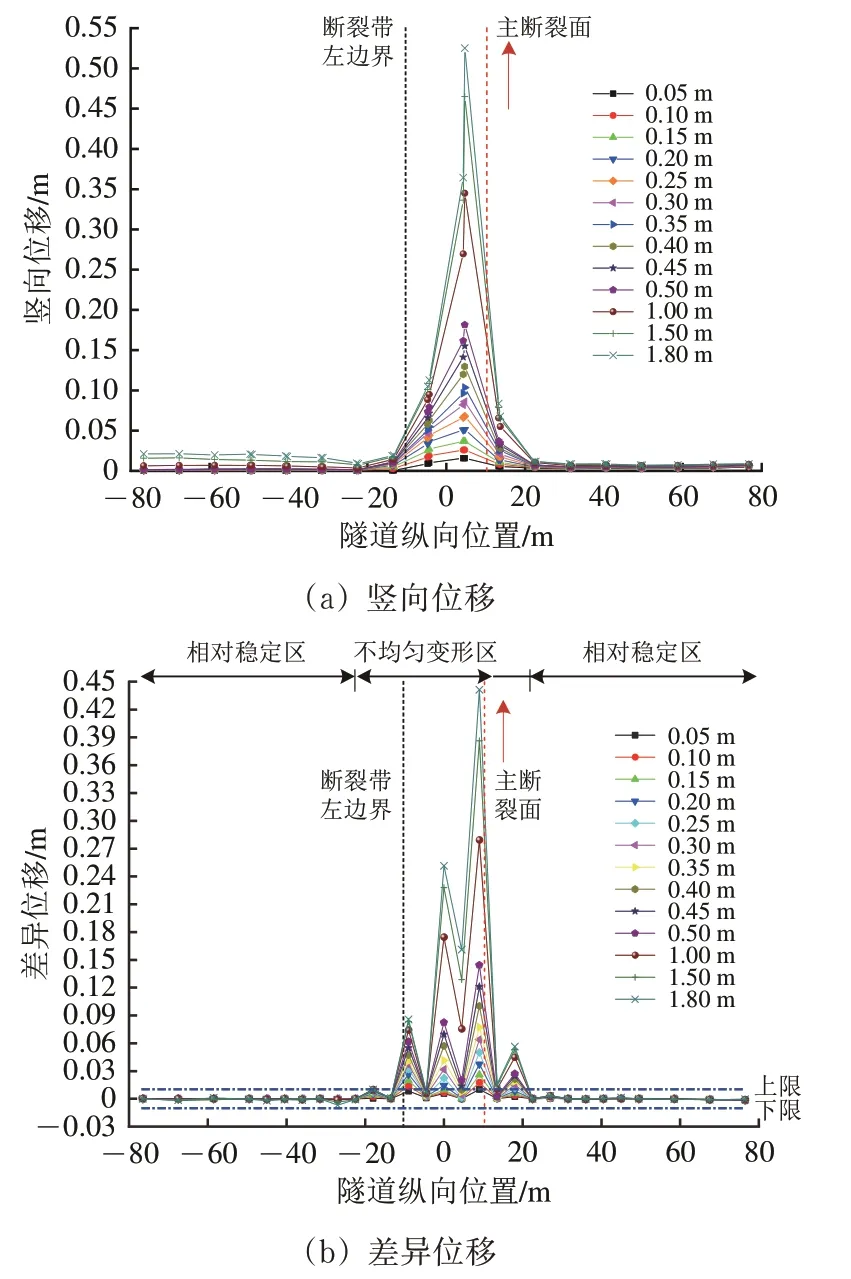
图11 仰拱底部竖向位移及差异位移（预留位错空间30 cm）

（1）受错动盘错动作用，围岩挤压剪切隧底衬砌结构，隧底仰拱较大竖向位移主要集中在断裂带及其两侧附近，呈倒“V”形。随着错动盘错动量不断增加，主断裂面附近两侧仰拱底部竖向位移的越来越大，如错动量为0.1 m 时仰拱底部上拱的最大值为26 mm，错动量为1.8 m 时的最大值为525.2 mm，达到前者的20.2倍。

（2）距离断裂带越远，错动盘侧和固定盘侧衬砌节段仰拱底部竖向位移逐渐减小至趋于平稳，位移值均为正、为上拱状态，而且固定盘侧仰拱底部竖向位移值基本都大于错动盘侧的。

（3）不同错动量下，竖向位移的显著性差异主要集中在断裂带及其两侧附近，差异位移极值为441.5 mm，位于主断裂面附近。错动量大于0.50 m后，显著性差异范围基本不变。不均匀变形区为固定盘侧距离断裂带左边界12.2 m 至错动盘侧距离主断裂面12.2 m范围内，其余为相对稳定区。

3）左拱脚水平位移

不同错动量下，各衬砌节段左拱脚的水平位移及相邻衬砌节段间的差异位移如图12 所示。由图12可得到如下结论。

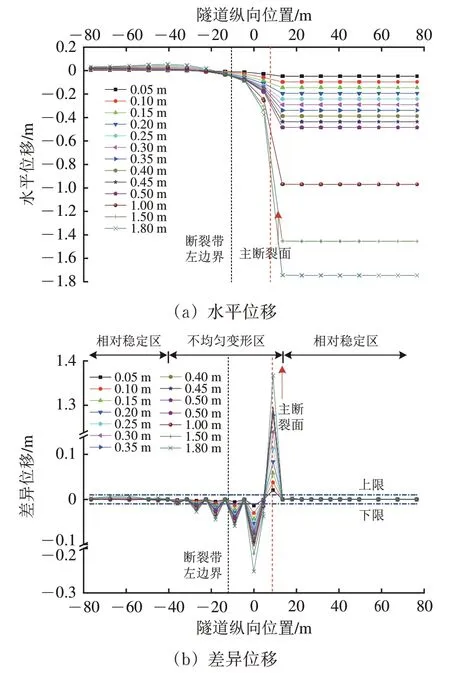
图12 左拱脚水平位移及差异位移（预留位错空间30 cm）

（1）左拱脚的较大水平位移主要集中在主断裂面附近，呈“S”形。随着错动盘错动量不断增加，错动盘侧衬砌左拱脚水平位移不断增大，主断裂面附近两侧衬砌左拱脚水平位移的差异也越来越大，如错动量为0.1 m 时左拱脚水平位移的最大值为96.7 mm，错动量为1.8 m时的最大值为1 746.2 mm，达到前者的18倍。

（2）距离断裂带越远，两端衬砌节段左拱脚水平差异位移越小。错动盘侧衬砌左拱脚水平位移下降至一稳定值，固定盘侧则逐渐上升至一平稳值；在隧道纵向-20～10 m 范围内，水平位移为负值，表明衬砌受断裂影响随之同向错动，在隧道纵向小于-20 m 后，水平位移为正值，可能与衬砌间相互挤压有关。

（3）不同错动量下，水平位移的显著性差异主要集中在断裂带及其两侧附近，差异位移极值为1 366.7 mm，位于主断裂面附近。错动量不小于1.50 m 时，显著性差异范围基本不变。不均匀变形区为固定盘侧距断裂带左边界28.60 m 至错动盘侧距主断裂面4.8 m范围内，其余为相对稳定区。

4）右拱脚水平位移

不同错动量下，各衬砌节段右拱脚水平位移及相邻衬砌节段间的差异位移如图13 所示。由图13可得到如下结论。

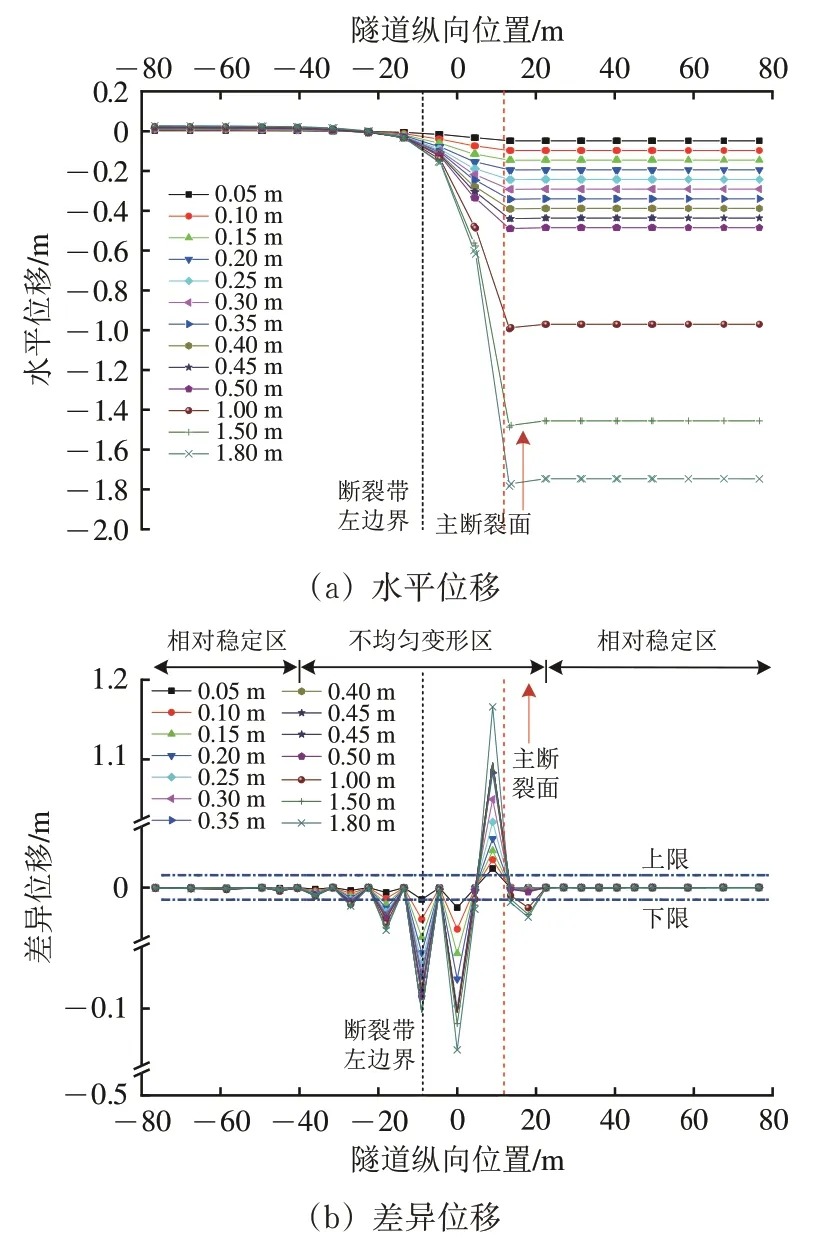
图13 右拱脚水平位移及差异位移（预留位错空间30 cm）

（1）右拱脚的水平位移分布及水平差异位移均与左拱脚的相似，错动量为0.1 m 时右拱脚水平位移的最大值为97.4 mm，错动量为1.8 m 时的最大值为1 783.3 mm，达到前者的18.3 倍；在隧道纵向-30～10 m 范围内，水平位移为负值，表明衬砌受断裂影响随之同向错动，而在隧道纵向小于-30 m 后，水平位移为正值，可能与衬砌间相互挤压有关。

（2）不同错动量下，隧道右拱脚水平位移的显著性差异主要集中在断裂带及其两侧附近，差异位移极值为1 166.0 mm，位于主断裂面附近。错动量不小于1.0 m 时，显著性差异范围基本不变。不均匀变形区为固定盘侧距断裂带左边界22.78 m至错动盘侧距主断裂面10.62 m 范围内，其余为相对稳定区。

5）断裂带两侧影响段长度

综上，隧道衬砌显著性位移主要集中在断裂带及其两侧附近，随着错动量的增加，衬砌节段之间的差异位移也越来越大。隧道拱顶竖向位移向下，呈“V”形；仰拱底部竖向位移向上，呈倒“V”形；左右拱脚的水平位移方向均与断裂错动方向一致，呈“S”形，但右拱脚的不均匀变形区范围要大于左拱脚的，这可能与右侧拱墙受地层错动直接作用、而左侧拱墙受间接作用有关。以±10 mm作为控制标准，不均匀变形区为固定盘侧距断裂带左边界28.6 m 至错动盘侧距主断裂面12.2 m 范围内，其余为相对稳定区。

穿越活动断裂带隧道设防范围分为断裂带核心段和断裂带两侧影响段，均应加强抗震和抗错设计。根据既有研究成果［11，13］，设防范围L的计算式为

式中：B1和B2分别为固定盘侧、错动盘侧的影响段长度，m；W为断裂带宽度，m。

对于该模型工况：断裂倾角90°、宽度20 m、与隧道轴向夹角76°，隧道衬砌长度9 m、变形缝宽度10 cm，在断面预留位错空间30 cm 方案下，得到断裂带两侧影响段长度分别为B1取28.6 m，约2.45D；B2取12.2 m，约1.05D。

3.3 隧道横断面上径向变形损伤

1）隧道横断面径向变形率

分别将开挖平衡后拱顶—仰拱底部、左拱脚—右拱脚、左拱腰—右墙脚和右拱腰—左墙脚4 处径向距离定为衬砌内径，得到不同错动量下对应位置的径向变形率曲线如图14 所示。图中：红色虚线和箭头分别表示主断裂面和错动方向；正、负值分别表示径向拉伸、压缩。由图14 可发现较大的径向变形率均出现在断裂带及其两侧附近，并进一步得到如下结论。

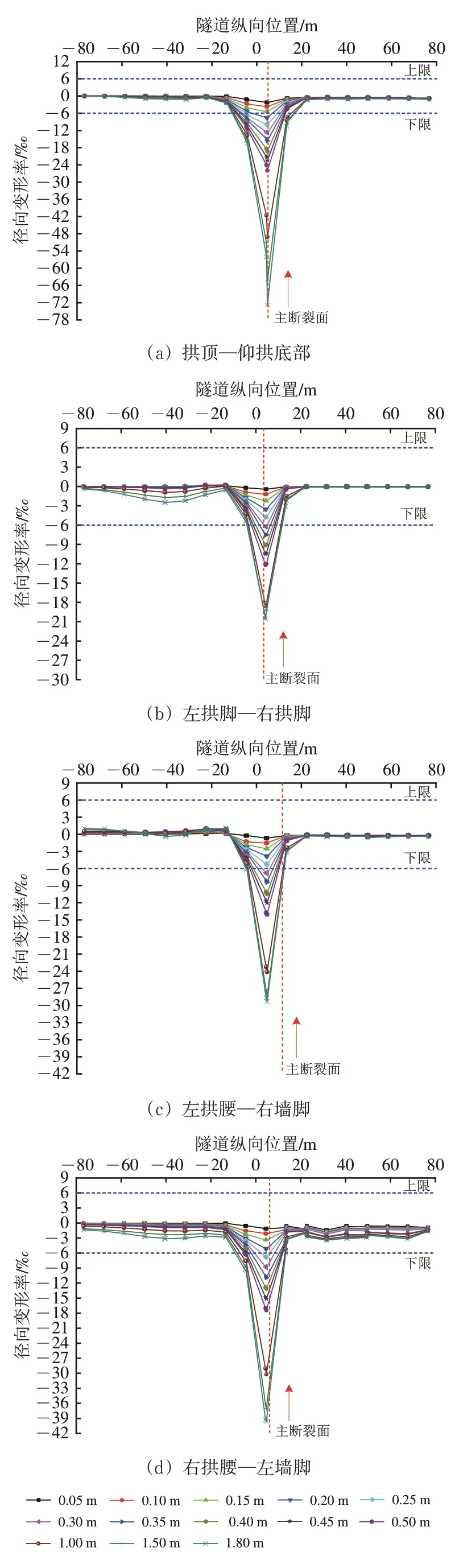
图14 隧道横断面径向变形率曲线（预留位错空间30 cm）

（1）对于拱顶—仰拱底部，径向变形率最凸出区间为固定盘侧-22.3 m 至错动盘侧31.3 m 范围内，拱顶—仰拱底部径向处于压缩状态；依据标准，错动量大于0.15 m 时，最大径向变形率超过损伤判定指标6‰。

（2）对于左拱脚—右拱脚，径向变形率最凸出区间为固定盘侧-13.7 m 至错动盘侧22.3 m 范围内；错动量不小于1.0 m 时，固定盘侧还有1 个径向变形凸起区域，区域内径向变形率为负，表明左拱脚—右拱脚之间径向处于压缩状态；错动量大于0.30 m时，最大径向变形率超过损伤判定指标。

（3）对于左拱腰—右墙脚，径向变形率最凸出区间为固定盘侧-13.3 m 至错动盘侧22.5 m 范围内；错动盘侧径向变形率为负，处于压缩状态；错动量不小于1.0 m 时，固定盘侧径向变形率为正，处于张拉状态，错动量大于1.0 m 时，固定盘侧-40 m 处径向变形率小于0，由张拉状态变为压缩状态；错动量大于0.30 m 时，最大径向变形率超过损伤判定指标。

（4）对于右拱腰—左墙脚，径向变形率最凸出区间为固定盘侧-13.7 m 至错动盘侧13.7 m 范围内；错动盘和固定盘侧径向变形率均为负，处于压缩状态；错动量大于0.25 m 时，最大径向变形率超过损伤判定指标。

2）变形后断面形态

根据前述径向变形，可刻画出变形前、后的隧道断面形态，其中典型的断面形态对比如图15 所示。由15 可知：固定盘侧，左拱脚—右拱脚和右拱腰—左墙脚的压缩变形相对较小，左拱腰—右墙脚为张拉状态；断裂带中间，隧道断面整体处于压缩变形状态，拱顶—仰拱底部的变形量最大，右拱腰—左墙脚次之；主断裂面附近，隧道断面变形量最大，拱顶—仰拱底部和左拱脚—右拱脚均处于压缩变形状态，左拱腰—右墙脚和右拱腰—左墙脚均处于张拉状态，隧道结构破坏也最为严重；错动盘侧，隧道断面整体处于压缩变形状态，拱顶—仰拱底部和右拱腰—左墙脚的相对变形相对较小。

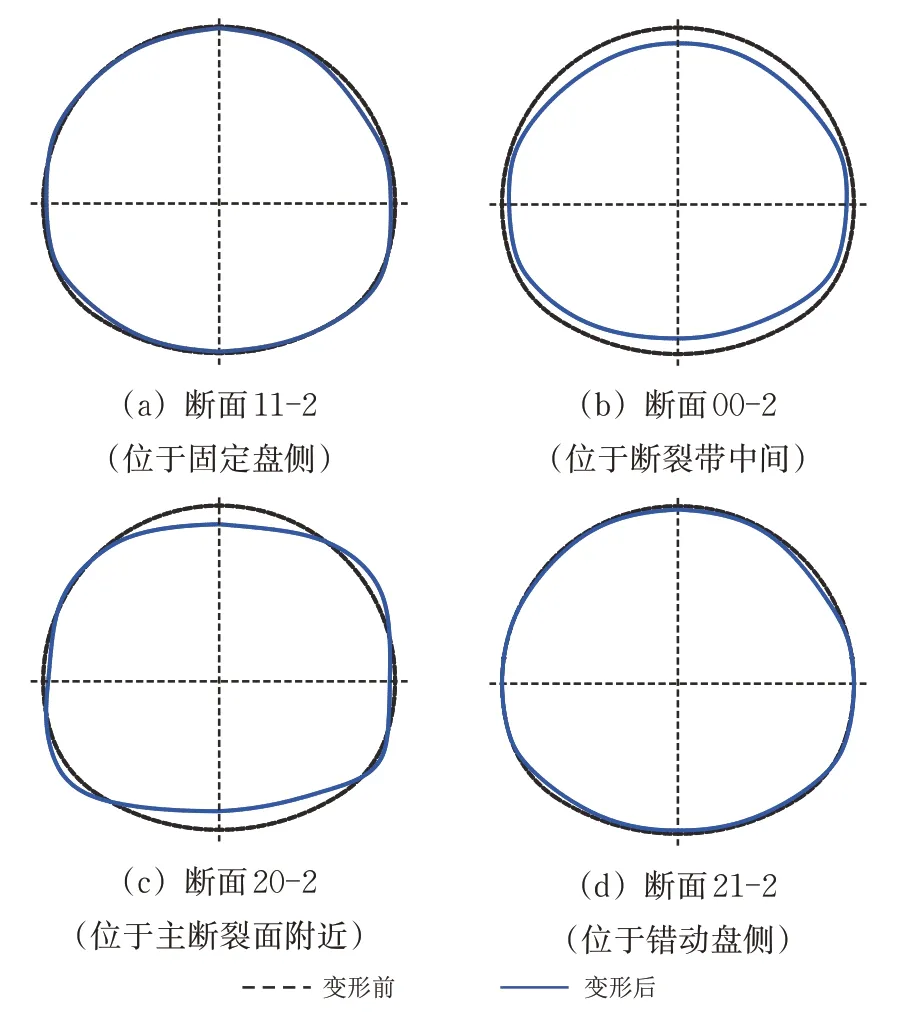
图15 变形前后的代表断面形态（预留位错空间30 cm）

3.4 不同预留位错空间下隧道衬砌响应规律对比

3 种预留位错空间方案下，隧道衬砌最大位移及衬砌节段之间的差异位移极值如图16 所示。由图16 可知：随着预留位错空间的增加，拱顶和仰拱底部的竖向位移均呈增加趋势，分别从320.7 和525.2 mm 增加到580.9 到548.1 mm，增幅分别为81.14%和4.36%；左拱脚和右拱脚的水平位移最大值变化范围较小，左拱脚减幅1.37%，右拱脚增幅0.7%，且右拱脚水平位移最大值更大；拱顶竖向差异位移极值和左、右拱脚水平差异位移极值均呈增加趋势，分别从282.3，1 366.7 和1 166 mm 增加到512.4，1 736.3和1 746.6 mm，增幅分别为81.51%，27.00%和49.80%，仰拱底部则变化相对较小，减幅2.0%。

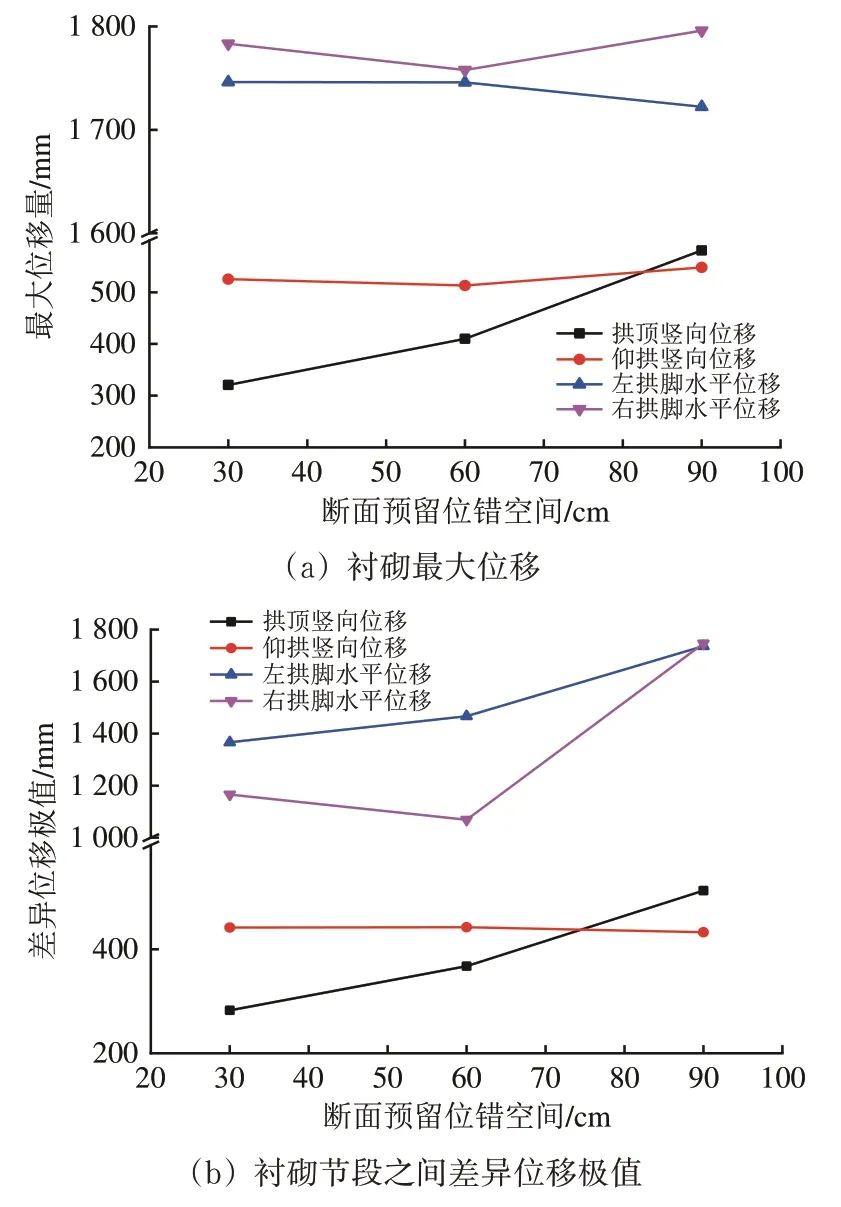
图16 不同预留位错空间下隧道衬砌最大位移及衬砌节段之间差异位移极值

3 种预留位错空间方案下，隧道衬砌影响范围及损伤破坏临界错动量如图17 所示。由图17 可知：随着预留位错空间的增加，错动盘侧影响长度B1和固定盘侧影响长度B2变化均较小，且B1大于B2，B1在2.5D水平波动，B2保持在1.2D水平；左拱脚—右拱脚和左拱腰—右墙脚的损伤破坏临界错动量曲线重合，除拱顶—仰拱底部始终保持在0.15 m外，随着预留位错空间的增加，其他3条临界错动量曲线均呈下降趋势，分别由0.30，0.30和0.25 m下降至0.15 m。

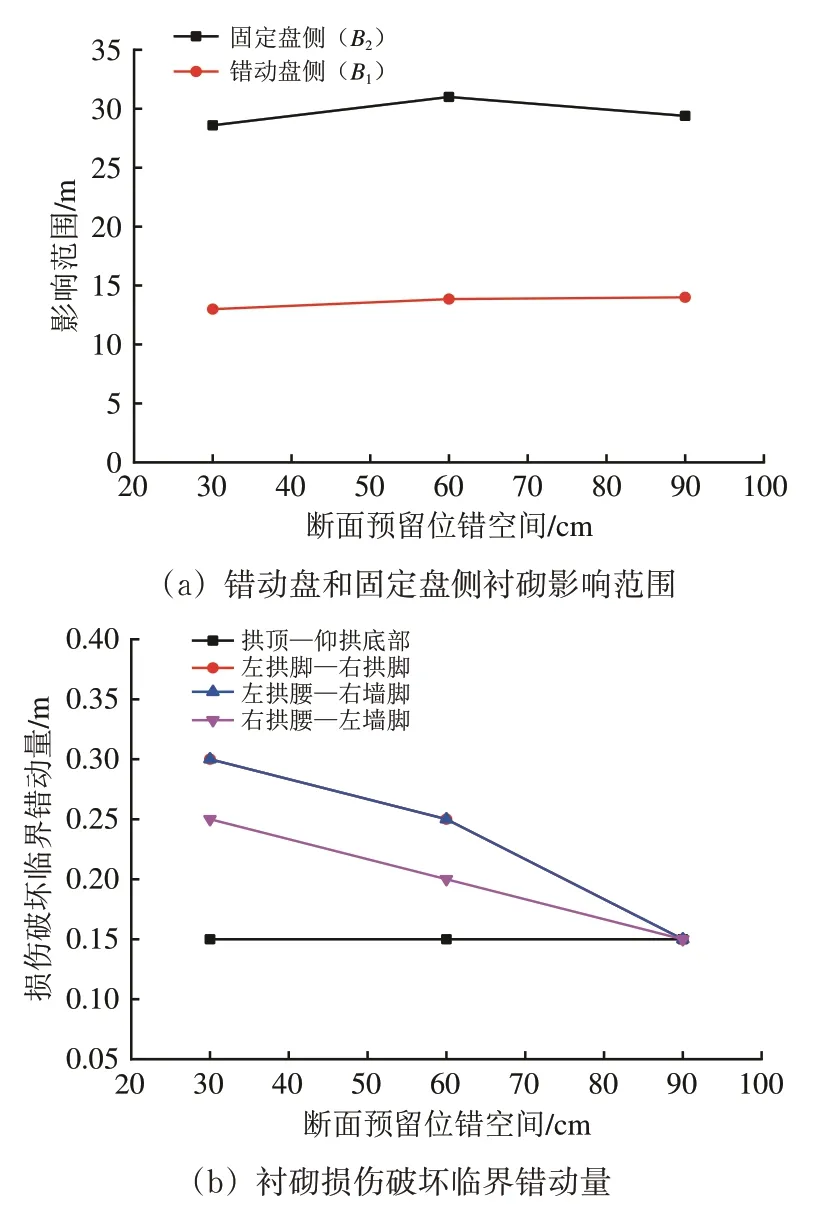
图17 不同预留位错空间下隧道衬砌影响范围及损伤破坏临界错动量

综上，随着断面预留位错空间增加，隧道衬砌位移也在不断增加，断裂带两侧衬砌影响长度基本不变，断面上衬砌关键节点间损伤破坏临界错动量呈降低趋势，不利于隧道结构抗措。

4 讨论

1）隧道横断面衬砌损伤破坏的临界错动量

受活动断裂的挤压、搓揉等构造作用，断裂带区域内围岩破碎，核心带内围岩甚至蚀变为泥沙状［31］。圆形隧道断面受力比较好，因此穿越活动断裂带隧道通常采用圆形或者类圆形断面型式。对圆形或类圆形隧道衬砌损伤破坏的临界错动量，文献［24］得出走滑断层左旋错动0.6 m 后隧道结构开始破坏，这与本研究及其他研究的结果差异较大，原因是其采用的衬砌破坏判断标准——最大剪应变取0.002 实际为混凝土压应变，见规范［29］条文6.2.1。文献［23］得出，当走滑断层错动10 cm 时，衬砌在断层滑动面附近达到严重损伤状态。文献［32］采用ANSYS 有限元分析软件得出，当走滑断层位错超过20 cm 时，隧道衬砌开始破坏。本研究以径向变形率6‰作为衬砌结构损伤判定指标，得出衬砌损伤破坏临界错动量为0.15 m，与多数研究的结果基本一致。

2）走滑型活动断裂错动作用下隧道断面响应

计算分析表明，走滑型活动断裂错动作用下，隧道衬砌拱顶和仰拱底部变形最为严重，这与文献［19］研究结果基本一致。因此穿越走滑型活动断裂带隧道的设计及施工过程需要重点加强隧道拱顶和仰拱部位。走滑错动量相同时，随着断面预留位错空间的增加，除拱顶—仰拱底部外，其他3 处的径向变形率都在增加，使得衬砌损伤破坏临界错动量变小，不利于结构抗错和抗震。这与文献［18］模型试验的结果一致。

3）穿越活动断裂带隧道断面扩挖的必要性当前穿越活动断裂带隧道（洞）已有一些成功实施案例，常用的首选设计思路是，根据活动断裂运动方式、活动速率等参数，估算出隧道（洞）服役期内（一般为百年）最大错动量，据此对隧道断面进行适当扩挖。前人与本文的研究成果均表明，扩挖隧道断面会降低隧道整体稳定性和抗错性能。但隧道穿越活动断裂带时必须预留足够的净空设防方案，以保证断裂错动后隧道断面补强空间［20，33］。

5 结论

（1）随着错动量的增加，断裂两侧衬砌整体位移差异越来越显著，影响范围越来越大，远离断裂的两端隧道衬砌间位移差异较小且整体稳定。较大的竖向位移集中在主断裂面所横跨衬砌的变形缝附近，错动量最大（1.8 m）工况下，衬砌拱顶下沉432.7 mm，仰拱底部上拱557.1 mm。

（2）明确了统一的隧道复合式衬砌结构位移及类圆形断面变形损伤控制标准。在纵向上，以±10 mm 作为衬砌节段间相对差异位移的控制指标，即衬砌节段间差异位移的绝对值大于10 mm时判定为不均匀变形区，反之判定为相对稳定区；在横断面上，参考城市地铁管片圆形隧道断面椭圆率，以径向变形率±6‰作为变形损伤状态判定指标。

（3）对于依托工程，隧道衬砌的显著性位移和径向变形率最凸出区间均主要集中在断裂带及其两侧附近。隧道拱顶竖向位移向下，呈“V”形；仰拱底部竖向位移向上，呈倒“V”形；左右拱脚水平位移方向均与断裂错动方向一致，呈“S”形。

（4）隧道衬砌节段间差异位移随着走滑型活动断裂错动量的增加而增大，断面上拱顶和仰拱底部变形最为严重。依据隧道结构变形损伤状态判定指标，以预留位错空间30 cm 方案为例，依托工程沿主断裂面走向的错动量大于0.15 m 时，拱顶与仰拱底部之间径向变形率超过判定指标6‰，隧道衬砌结构将发生损伤破坏。设计及施工过程中须重点加强拱顶和仰拱部位。

（5）随着断面预留位错空间由30 cm 增加到90 cm，衬砌位移极值也在不断增大，但断裂带两侧隧道衬砌影响长度基本不变，固定盘侧影响长度约为2.5 倍隧道跨度，错动盘侧影响长度约为1.2倍隧道跨度；断面上关键节点之间损伤破坏临界错动量呈减少趋势，除拱顶—仰拱底部外，其他关键部位间损伤破坏临界错动量减少到0.15 m，这对隧道结构抗措不利。隧道穿越活动断裂带时必须预留足够的净空设防方案，以保证断裂错动后隧道断面补强空间。