焊接机器人的摆动焊接轨迹规划策略研究

杨亮亮，方世坛

(浙江理工大学机械工程学院，浙江 杭州 310018)

0 引言

焊接机器人作为通用工业机器人，在机械制造生产中起到了重要的作用，如在汽车制造业、造船业和航空航天行业[1]等行业中焊接机器人极大地提升了生产效率。运行效率是工业生产的重要指标之一，因此，焊接机器人想要进行高效简明的运动则需要有合适的焊接路径和轨迹规划算法，焊接机器人的路径轨迹规划指的是在始末位置和示教位置已知的前提下规划焊接的路径。对于焊接轨迹规划，早在1997年Abdel-Malek和Yeh[2]提出了一种数学分析计算方法来验证机械臂在空间运行轨迹的准确性和完整性，确保机械臂焊接过程和焊缝的完整；1999年，Wurll等[3]提出了六自由度工业机器人点到点轨迹规划的最优轨迹规划方法，进一步提高了焊接机器人的焊接效率；2006年，王晓峰[4]提出将弧焊机器人焊接姿态与焊接工艺参数联合进行焊接轨迹规划的方法；2011年，陈鲁刚等[5]通过ADAMS软件求解焊接机器人的逆运动学，为焊接机器人的轨迹规划提供了一条快捷的途径。

焊接轨迹涉及到多阶段轨迹的连续性和稳定性，因此在完成路径规划之后，轨迹规划仍需要考量最优轨迹的情况，即在多段焊接轨迹中运行效率最优的情况。最优轨迹规划的优化指标主要有能量最优和时间最优2种。在能量最优方面，Hirakawa于1996年采用了变分法和B样条曲线法，对焊接机器人系统消耗的能量进行了最优化处理。在实际应用中出于工艺生产效率的需求，时间最优的轨迹规划的研究要更加热门。在时间最优方面，Chen等[6]提出了一种基于机器人在位置、速度、加速度和二阶加速度方面的运动学约束；在相同的运动学约束下，Bazaz等[7]等也提出了相似的规划方法，但他们用带有光滑转折的折线将关节空间中的关键点连接到一起；2021年，李龙辉等[8]提出并验证了四阶多项式速度曲线为稳态时间和残余振动最优的多项式速度曲线，上述文献在点到点的轨迹规划和多阶段轨迹中优化了算法，提升了运行效率，但在摆动焊接实际运用中需要保证多阶段轨迹的精确度，不能采用转角圆弧化过渡的方式。

因此，本文基于嵌入式STM32H7平台和VS2019平台开发焊接机器人控制系统，设计了空间直线摆焊和空间圆弧摆焊的算法，为用户操控焊接机器人完成空间摆动焊接功能提供了一种方案。

1 焊接工艺路径规划策略

机器人的焊接轨迹规划包含路径规划和轨迹规划2部分，在进行轨迹规划的前提下首先要对末端的路径规划策略进行研究。

进行路径规划之前，对机器人插补运动的方法进行概述。焊接机器人的轨迹插补包含了位置、速度和加速度的插补，在文献[9]中提出了笛卡尔空间下的直线插补方法和圆弧插补方法，机器人的姿态和位置采用等时插补[10]的方式将起点至终点的位姿均分至每个插补点上，这样即可获得空间直线和空间圆弧的插补轨迹。在插补理论的基础上，焊接工艺路径规划是基于已知轨迹和用户通过示教选定的参数来自动规划焊接路径，焊接工艺针对焊缝的路线分成直线摆焊和圆弧摆焊，本文主要针对这2种摆焊路线设计策略。

1.1 空间直线摆焊路径规划策略

空间直线摆焊是在用户已经给以机器人运动范围内的空间起点和终点的前提下，用户通过操作机器人至示教点以获取焊接轨迹的参数，根据设计的算法从起点开始根据已知参数计算下一个点并且运动，机器人循环运动直至到预设的终点为止。直线摆焊的路径规划策略如图1所示。

图1 直线摆焊路径规划

图2 罗德里格旋转示意图

直线摆焊路径规划过程可以分为起始阶段t1、中间阶段t2和结束阶段t3。起始阶段t1是以起点Ps作为运动的起始点，用计算出的向量作为参数计算出空间中的P1点，并且结合空间直线插补的方式运动到P1点，接着以P1为起点进入中间阶段t2，根据向量按照顺序依次周期计算运动直到运动到未满1个周期的情况，以图3为示例就是P7点处。

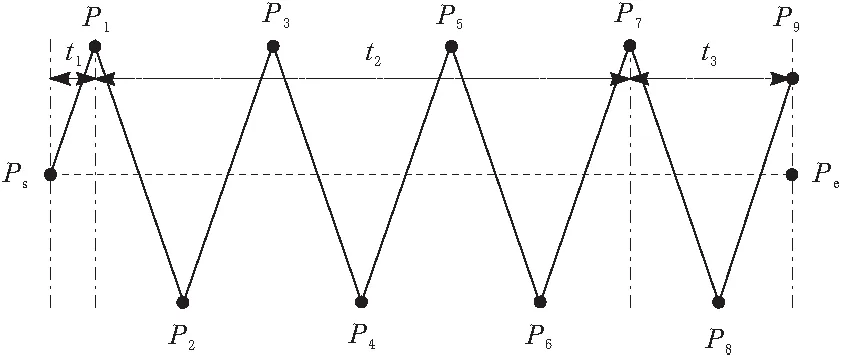
图3 空间直线焊接轨迹

最后进入结束阶段t3，在t3阶段由于经过t1和t2阶段之后，范围长度|PsPe|剩下的长度不满1个周期，就要根据剩余范围长度，如图4所示，P7点作为t2阶段结束时的终点，同时也作为t3阶段的起点，分以下几种情况进行讨论：

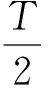
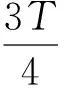
通过上述的策略，可以在已知起点、终点和示教点的前提下，来确定空间直线摆焊的所有中间点，完成空间直线运动的摆焊路径规划。

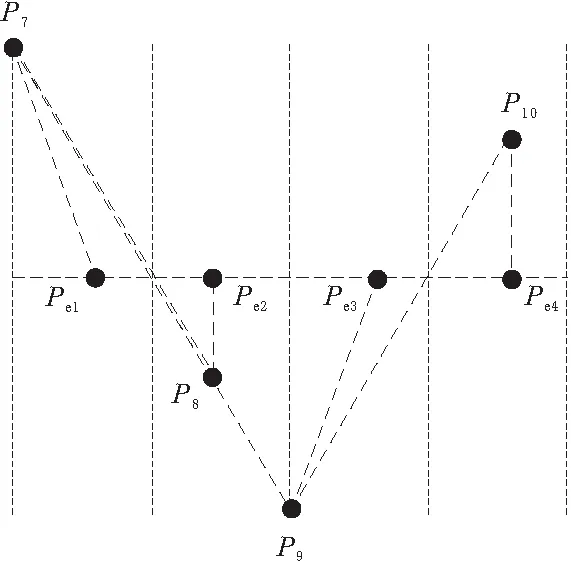
图4 t3结束阶段

1.2 空间圆弧摆焊策略

空间圆弧摆焊的路径规划策略需要先获取空间圆弧运动路径，空间圆弧运动路径是通过空间起点、弧点和终点来确定的，获取这3个点之后首先需要对这3个点进行共线判断，在不共线的条件下圆弧能够形成，接着用户通过示教焊接机器人到示教点以获取焊接参数，在获取示教点的时候需要进行4点共面的判断以及示教点是否在圆弧的判断，当4点共面且示教点不在圆弧的弧线上时，则进入空间圆弧摆焊的焊接参数计算过程，如图5所示。

图5 空间圆弧摆焊参数计算

图6 初始向量

在获取了参数之后需要根据已知参数计算焊接中间点，将向量PwcPwsH和PwcPwsL在平面内旋转，旋转的角度通过索引和夹角参数θω的乘积来确定。如果要进行旋转，首先要根据已知的2个不共线的向量PwcPws和PwcPwe来确定运动平面的单位法向量，然后通过图2所示的罗德里格旋转公式来对向量PwcPwsH和PwcPwsL进行旋转，其中要注意平面的单位法向量的方向要遵守右手定则，这样可以使旋转的方向为正方向。最后能得到如图7所示的空间圆弧摆焊轨迹，其中，起点至终点之间的中间点集合是由向量PwcPwsH和PwcPwsL按照索引旋转得到的。

图7 空间圆弧摆焊轨迹

空间圆弧摆焊插补运动过程也需要分为3个运动阶段：开始阶段T1、中间阶段T2和结束阶段T3。在开始阶段T1中，将图6中PwcPwsH旋转角度θω之后，接着进入T2中间阶段，将索引和周期角度θT结合旋转向量PwcPwsH和PwcPwsL得到中间点直到剩余角度θr不满一个角度周期θT。最后进入结束阶段T3，在结束阶段中需要根据剩余角度θr分4种情况讨论：

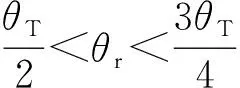
图8 结束阶段的4种情况

上述方式可以在圆弧轨迹已知的前提下，确定在同一平面内取参数计算点来确定空间圆弧摆焊的轨迹。

2 焊接轨迹规划

实际生产中需要考虑机器人各关节的速度和加速度的连续问题，使得机器人在快速到达目标位置的同时减小机械振动。因此，本文提出了对机器人点到点的轨迹规划方法和多阶段轨迹之间的速度过渡策略。

2.1 S形加减速轨迹规划

常见的S形加减速包含梯形加减速曲线和余弦加减速曲线，这些方法有效降低了机器人运行时的残余振动和稳态时间，在一定程度上提高了运行效率。但这些方法仍然存在局限性，梯形速度曲线为非光滑的轨迹曲线，激发的残余振动会降低执行机构的寿命，且产生较大的误差;余弦加减速曲线在运行轨迹复杂或者运动轨迹过长时会使得运算量增大，这就要求控制器性能有较高的要求。

本文参考了文献[11]中始末速度不为0的加减速控制算法，将空间点到点的运动分为加加速、匀加速、减加速、匀速、加减速、匀减速和减减速段。焊接轨迹中间点的速度规划可以获取全部中间点的速度，在系统允许的最大速度、加速度和加加速度的约束条件下，给定始末速度和轨迹长度，分别规划7段加减速过程中的时间。

2.2 中间点速度规划

摆动焊接可以将整个摆动焊接运动分割成各个点到点的直线运动，通过算法获取空间中的各摆动焊接中间点，中间点的速度规划是指在多阶段轨迹中根据所求中间点处的转角角度和中间点前后的轨迹长度来对中间点处的速度进行规划。空间直线摆焊中需要根据图1中计算的旋转角度θ得到中间点的转角为θco=2θ。在实际运动中，出于时间最优方面的考虑，机器人在中间点前后速度之比越接近1则运行时间越短，但由于机器人在中间点处转折加速度和速度过大时会产生机械振动，所以需要考虑转角角度来对中间点的速度进行约束，转角角度如图9所示。

图9 转角角度

在约束关系中，当转角角度θco大于90.00°时，为了解决速度过大时在转角处产生机械振动，速度必须为0，在转角角度θco小于90.00°时，约束关系的表达式为

Amax为系统最大加速度；Ts为插补时间；转角角度θco已知且与θcb为互补角。速度规划首先考虑轨迹长度对中间点速度的约束，始末速度不为0的S形加减速轨迹规划，可以将7个阶段的轨迹长度根据不同的约束条件获取临界长度，如根据初始速度Vs、最大加速度Amax、最大速度Vmax可以得到加加速度阶段的临界长度Laa，将各阶段的临界长度求取后再判断现有轨迹长度位于S形加减速的哪个运动阶段。由于在焊接轨迹的t3阶段中可能存在轨迹长度极短的情况，前瞻的方法会使得最后一段轨迹无法正常完成，所以轨迹长度对速度规划采用前瞻反向寻优法，即从起点开始计算每个中间点在轨迹长度的前瞻速度Vf后，从终点反向计算每个中间点的速度Vb，最后取每个中间点的最小值即可完成轨迹长度约束下的中间点速度规划。完成轨迹长度对中间点的速度约束之后，需要考虑转角角度对中间点速度的约束，图3中得知在直线摆焊的3个阶段只需要得到最后一个中间点和t1、t2阶段中间点2个转角角度即可得到所需的转角角度，最后一个中间点的转角角度可以通过已知点的向量关系来计算得到。在获取了2个转角角度之后，从终点开始根据当前的轨迹长度依次反推中间点的最大允许速度。最后取转角角度和轨迹长度约束条件下的最小速度，即可得到每个中间点的最大允许速度，从而完成中间点的速度规划。

3 MATLAB验证路径算法

3.1 空间直线摆焊

通过MATLAB软件可以验证空间直线摆焊路径规划的正确性[12]，在程序中输入起点、终点和示教点的坐标作为算法的输入参数，可以得到如图10所示的空间直线摆焊轨迹。此时图10中起点为[100.00 mm,200.00 mm,300.00 mm]，终点为[200.00 mm,300.00 mm,400.00 mm]，示教点为[195.80 mm,280.00 mm,410.00 mm]。

图10 空间直线摆焊MATLAB仿真

3.2 空间圆弧摆焊

空间圆弧摆焊的轨迹需要将起点、弧点、终点和示教点来进行参数计算，在确定4点共面且形成圆弧的3点不在同一条直线上时，根据示教点获取参数后进入空间圆弧摆焊的中间点，空间圆弧摆焊的轨迹仿真如图11所示，此时起点位置为[400.00 mm,0,0]，弧点位置为[450.00 mm,50.00 mm,0]，终点位置为[500.00 mm,0,0]，示教点的位置为[510.00 mm,5.00 mm,0]，图10和图11中坐标为机械臂末端在空间中的工具坐标系。

图11 空间圆弧摆焊MATLAB仿真

3.3 时间最优的多段S形轨迹曲线仿真

在轨迹规划当中，机器人末端以S形加减速曲线进行运动，通过雅可比矩阵可以实现末端速度与关节速度、末端加速度和关节加速度之间相互转换。在轨迹规划当中利用雅可比矩阵可以将操作空间的速度转换为关节速度。以空间直线摆焊的路径为例，此时转角大于90.00°，根据速度角度约束关系可以得到转角需要将速度约束为0，因此，在约束条件下起始速度和终止速度均为0，位移为45.50 mm，Vmax为0.01 m/s,Amax为0.01 m/s2,Jmax为0.01 m/s3，经过7段S形加减速算法计算可得当前条件下的运行时间为6.550 s，根据第1.1节将整个焊接运动分为3段，因此完成这段空间直线摆焊运动时间为75.570 s。

将起点、终点和示教点另取1组参数使得转角角度小于90.00°，此时起点为[100.00 mm,200.00 mm,300.00 mm]，终点为[200.00 mm,300.00 mm,400.00 mm]，示教点为[190.80 mm,294.60 mm,391.70 mm]，根据已知参数求得转角角度为24.40°，如果采用优化前点到点的始末速度均为0的方法，此时3段的时间分别为3.515 s、28.284 s和2.144 s，完成整段焊接运动共计33.943 s，第2.2节计算时间最优的算法可以得到3段的时间分别为3.479 s、27.858 s和2.086 s，完成这段直线摆焊运动的时间共计33.423 s，相较于始末速度为0的算法提升了0.520 s，效率提升1.50%。

4 实验平台搭建

本文提出的焊接轨迹规划算法搭载于一个完整的机器人控制系统[13]，控制系统由工业机器人示教软件、基于STM32H7和FPGA的运动控制卡、电机驱动器和SCARA机器人本体组成。系统的框图和SCARA机器人实验平台分别如图12和图13所示。

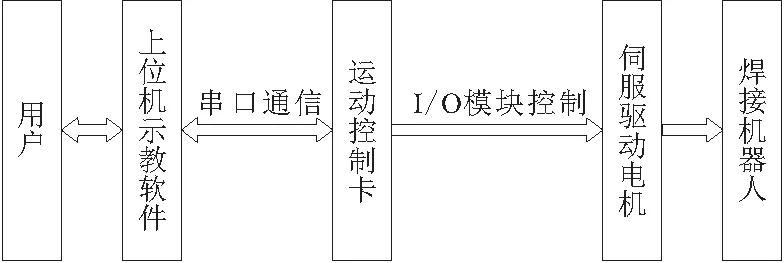
图12 控制系统

图13 SCARA机器人实验平台

示教器作为连接操作人员和机器人控制系统的关键部分，它的性能将很大程度上决定工业机器人的工作效率[14]，本上位机示教软件是基于Windows平台中VS2019和.NET框架开发的，由程序编辑模块、运动控制模块、消息模块、状态监控模块、参数设置模块、外部设备管理模块和软键盘输入模块组成。

实现焊接功能的具体流程如图14所示。

图14 焊接功能流程

在图13的SCARA机器人实验平台中，下位机能将位置信息实时传至上位机，通过读取上位机中反馈的位置数据可以得知机器人的空间摆焊的中间点。在上位机示教软件中，下发焊接运动指令的同时开启定时器，并在运动结束后关闭定时器并读取时间参数可以获取完成整段焊接运动所需的时间，以此方法可以比较优化前和优化后完成同一段焊接运动所需的时间，以空间直线摆焊为例，始末位置和示教位置分别为[100.00 mm,200.00 mm,300.00 mm]、[200.00 mm,300.00 mm,400.00 mm]、[190.80 mm,294.60 mm,391.70 mm]，此时下发焊接运动命令优化前和优化后的时间分别为34.914 s和34.273 s，时间节约了0.641 s，效率提升1.84%，相较于仿真存在一些误差。

5 结束语

本文基于STM32H7和SCARA机器人实验平台，着重介绍了焊接机器人摆动焊接的轨迹规划策略，并且在基于S形轨迹规划算法的基础上提出了对摆动焊接轨迹中转角速度进行约束的方法，相较于传统的始末速度为0的S形轨迹规划算法，该方法能够有效地提升时间效率，仿真和实验结果能够有效地证明焊接轨迹的准确性和一定程度上提升了时间效率。本文设计的焊接机器人的轨迹规划策略在实际生产中已得到应用，具有一定的实际意义和参考价值。