改进粒子群算法在柔性作业加工时间问题研究
2023-02-15曲鹏举
曲鹏举
(贵州理工学院工程训练中心,贵州 贵阳 550003)
0 引言
近年来,柔性作业加工已经在微电子、小批量零件等领域得到广泛应用,柔性作业车间生产问题(flexible job-shop processing problem,FJPP) 也成为了制造领域重点研究的问题之一,柔性作业加工时间问题就是其中的关键。
粒子群算法由于参数少,操作简单,已经广泛应用于柔性加工问题中。顾幸生等[1]对柔性作业车间调度问题中的多个性能评价指标进行研究后,提出了改进博弈粒子群算法;Ismayilov等[2]为解决工作流多目标优化问题,提出了一种基于预测的动态多目标进化算法;马学森等[3]针对传统粒子群算法求解云计算多目标任务调度的收敛速度慢、精度低的缺陷,提出一种优化多目标任务调度粒子群算法(MOTS-PSO);崔航浩等[4]针对以最小化最大完工时间为目标的MRC-FJSP,提出了一种带随机网络的多种群粒子群优化算法;张闻强等[5]针对多目标FJSP求解过程复杂、算法易陷入局部最优的问题,提出了一种基于多区域采样策略的混合粒子群优化算法;张立果等[6]针对大多数算法求解多目标柔性作业车间调度问题时,所存在的稳定性差、搜索深度不够、无法对多目标中单一目标进行深入搜索的问题,对传统遗传算法做出改进,提出了一种求解多目标问题的双层遗传算法;Dong等[7]为解决传统粒子群优化(PSO)中的早熟收敛问题,提出了基于对立策略的的自适应变异粒子群优化(AMOPSO);胡志刚等[8]针对有效解决云环境中任务分配问题从而有效降低能耗,提出了一种改进的粒子群优化算法。
贝塔分布作为统计学上的概率分布,在粒子群算法的优化问题中的应用也逐渐增加。胡棠清等[9]为解决粒子群优化算法中存在的早熟收敛、易陷入局部寻优等问题,提出一种对惯性权重的非线性改进策略,构造了一种基于指数函数的惯性权重,并加入服从贝塔分布的随机调整数,以实现对其动态调整;周蓉等[10]针对粒子群算法(PSO)易早熟收敛、逃离局部最优能力差、精度低等缺点,提出一种基于灰狼优化的反向学习粒子群算法,该算法非最优粒子采用贝塔分布,提高其搜索效率和开采性能;黄洋等[11]提出了一种动态调整惯性权重的简化均值粒子群优化算法(DSMPSO),该算法构造了一种基于余弦函数的惯性权重,并加入服从贝塔分布的随机调整策略,以实现对惯性权重的动态调整,从而更好地平衡算法的全局和局部搜索能力;王勇亮等[12]在收敛因子和种群位置更新公式中引入三角函数和贝塔分布,提高了算法后期的收敛速度。
为了减少柔性作业加工时长,本文提出一种改进粒子群算法(β-PSO)。
1 问题描述及模型构建
1.1 柔性作业加工问题模型
柔性作业加工问题定义:已知有n个待加工工件,在m台可用机器设备上进行加工,每个工件有m道工序需要加工,每个工件的加工工序以及加工耗时已知,在符合柔性作业加工时间问题约束条件下,使总体加工时间最短。
柔性作业加工时间问题模型描述如下:
a.待加工的工件集J={J1,J2,J3,…,Jn},车间加工可使用机器集M={M1,M2,M3,…,Mm},其中最大工件数为n,最大可用机器数为m。
b.每个工件加工工序不同、加工顺序固定,工序集合P={Pi|P1,P2,P3,…,Pn},{i|i=1,2,3,…,n},Pi为编号为i的工件的所有工序,Pij为编号为i的工件的第j个工序。
c.STijk、Fijk、Cijk分别为工件i的第j道工序在k号机器的加工起始时间、加工结束时间与加工持续时间,其中{k|k=1,2,3,…,m}。
d.Tk为k号机器实际运行时间,Fmax为所有工件的全部工序完成的最后结束时间。
柔性作业加工时间的优化目标是在接近实际生产的环境下,尽可能把各种机器、所有工件和所有工序做到合理分配,使Fmax全部工序完成的最后结束时间最短,确定的加工时间目标函数为
minFmax=min{maxTk}
(1)
1.2 柔性作业加工时间问题约束条件
在全部工序加工过程中,加工可使用机器可以为任意待加工工序提供支持。根据机器加工的工艺流程以及实际加工中各项工序的完成顺序,特定的机器按照工艺流程、工艺卡片,同一时间只能进行某种工序的加工。在保证紧前工序完成之后,才能进行下一个加工时间的确立。因此,加工的约束必须满足下列条件,即:
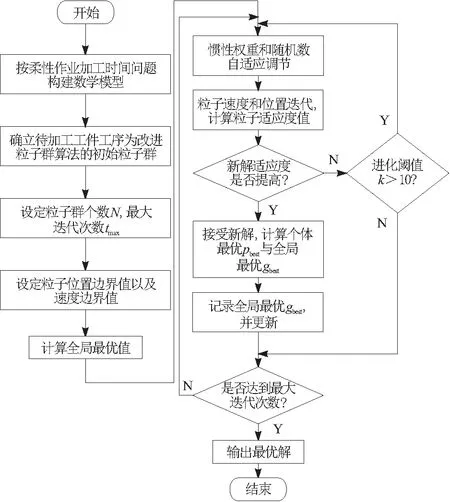
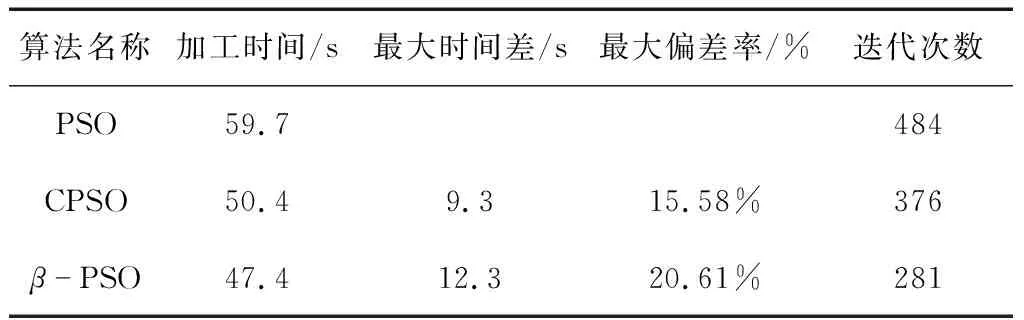
Fijk-Fi(j-1)k≥Cijk1 (2) Fabk-Fijm≥Cabk (3) Fijm≥Cijk (4) 式(2)表示所有工件的工序都需要消耗时间,必须按照特定的顺序完成;式(3)表示机器不重复占用原则,任意1台机器不能在同一时间内完成多个工序;式(4)表示加工持续时间的约束。 粒子群优化算法(particle swarm optimization,PSO)是一种典型的群体智能优化算法。该算法因为编程简单、参数且时间复杂度低而广泛应用于众多领域。标准的粒子群优化算法位置和速度状态属性为: (5) (6) 2.2.1 粒子群算法惯性权重的改进 惯性权重对粒子群算法的收敛速度及收敛质量有重要影响,为了解决标准粒子群算法求解过程中收敛性缓慢、稳定性低和易陷入局部最优等缺点,惯性权重不应该是固定值,而应该随着迭代次数的增加,前期有较大的惯性权重,加强全局寻优能力,后期有较小的惯性权重,局部寻优能力较强,所以本文提出惯性权重幂函数自适应调节方法,即 (7) ωmax为惯性权重的最大值,ωmin为惯性权重的最小值,ωmax=0.95,ωmin=0.40;tmax为最大迭代次数;t为当前迭代次数。 2.2.2 粒子群算法随机数的改进 标准粒子群算法中r1、r2为(0,1)内均匀分布的随机数,而统计学中贝塔分布也是一个在[0,1]内连续分布的概率数,被广泛应用于机器学习和数理统计学[13]。贝塔分布的概率密度函数为: (8) (9) 其中a>0,b>0。a、b取值不同,贝塔概率分布的图像也不同。若a=b,函数关于x=0.5直线对称;若a>b,图像靠右侧,相反靠左侧。 根据式(7)、式(8)和式(9)改进后的粒子群算法公式为: (10) (11) 改进粒子群算法流程如图1所示: a.按照柔性作业加工时间问题模型及约束条件式(1)~式(4),构建数学模型。 b.初始改进粒子群算法迭代次数t=1,设定算法参数、位置边界值和速度边界值,包括粒子个数N、最大迭代次数tmax、初始粒子位置xi、初始粒子速度vi、位置边界值xmax、速度边界值vmax以及维数D。 c.按照粒子群算法惯性权重幂函数调节式(7)和贝塔分布随机数式(8)、式(9)自适应改变参数ω(t)和r1、r2,根据速度公式(10)和位置式(11)进行迭代,计算粒子的适应度值,选出当前最优解。 d.设定算法进化阈值k=10,若个体最优值在一定迭代次数未发生变化,判定算法早熟,按照步骤c继续进行更新。 e.判断是否达到最大迭代次数tmax,若达到则输出当前最优值,若未达到,则迭代次数t+1,返回步骤c继续迭代。 图1 改进粒子群算法流程 为验证改进粒子群算法(β-PSO)的性能,在Win7操作系统,配置计算机Intel(R) Core(TM) i5-3470 CPU @3.20 GHz,8 GB RAM,MATLAB(R2014a)环境下,选取Kacem算例[14],将β-PSO与标准粒子群算法(PSO)、余弦惯性权重改进粒子群算法(CPSO)[15]的仿真结果进行对比,结果如表1和表2所示。算法参数取:粒子群粒子个数N=30,最大迭代次数tmax=600。最大时间差为各算例中,加工时间最长的算法与加工时间最短的算法的差值;最大偏差率为各算例中,最大时间差与最长加工时间的比值。最大时间差和最大偏差率反应了算法改进后的效果。 从表1 Kacem算例加工时间分析可知,随着工件数n、机器数m的增加,加工时间随之增长。标准PSO算法参数没有进行改进,惯性权重采用固定值,随机数采用(0,1)均匀分布,4个KACEM算例中,PSO算法的加工时间都是最长的,在第1个算例中,工件数n=6,机器数m=6,加工时间最长的是PSO算法,最短的是CPSO算法,最大时间差为4.2 s,β-PSO算法比加时间最短的CPSO算法多了0.2 s;在第2个算例中,工件数n=8,机器数m=8,加工时间最长的是PSO算法,最短的是β-PSO算法,最大时间差为6.7 s;在第3个算例中,工件数n=10,机器数m=10,加工时间最长的是PSO算法,加工时间为59.7 s,最短的是β-PSO算法,时间为47.4 s,最大时间差为12.3 s;在第4个算例中,工件数n=15,机器数m=10,加工时间最长的是PSO算法,加工时间为96.7 s,最短的是β-PSO算法,时间为74.2 s,最大时间差为22.5 s。在4个算例中,机器数与工件数较少的时候,β-PSO算法比CPSO算法加工时间略低,随着机器数与工件数的增加,β-PSO算法在加工时间上相较其他2种算法的优势逐渐体现出来。 表1 Kacem算例加工时间对比 由表2可知,在Kacem03算例中,β-PSO算法最大偏差率为20.61%,CPSO算法最大偏差率为15.58%。β-PSO算法比CPSO算法降低了3 s,降低了5.95%。 表2 Kacem03算例各算法加工信息 β-PSO算法在迭代次数t=281次时寻得最优解, 而CPSO在迭代次数t=376次、PSO在迭代次数t=484次时寻得最优解,β-PSO算法与其他2种算法相比具有更好的寻优性能。 针对柔性作业车间加工时间问题,本文提出β-PSO算法,该算法以最小加工时间为目标函数,惯性权重幂函数自适应调节,随机数采用贝塔分布进行改进,提升算法的全局和局部搜索能力,可以有效改进标准粒子群算法求解过程中收敛速度慢、寻优稳定性差、易过早陷入局部最优等。 选取Kacem经典调度算例,将β-PSO算法与PSO、CPSO算法仿真验证,从最小加工时间、最大时间差和最大偏差率3个角度分析了β-PSO在求解Kacem算例的性能,验证了β-PSO算法的在解决柔性作业车间加工时间问题上的优越性。2 改进的粒子群算法
2.1 标准粒子群算法
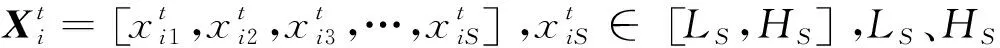
2.2 粒子群算法参数的改进
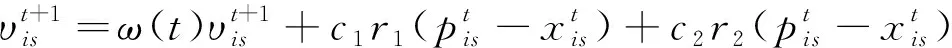
2.3 改进粒子群算法流程
3 仿真分析与案例验证

4 结束语
