低温氮气中液滴喷雾冻结过程的研究
2023-02-14彭润玲翟浩楠刘锦悦郭俊德
彭润玲,翟浩楠,杨 杰,王 威,刘锦悦,曹 蔚,郭俊德
(西安工业大学 机电工程学院,西安 710000)
0 引言
喷雾冷冻干燥技术是将物料经雾化器雾化后与冷介质接触快速冻结成冰粒,然后在低压环境中将冰粒脱水干燥的技术[1]。该技术兼有冷冻干燥与喷雾干燥的优点,广泛应用于纳米材料、粉状食品和药品的制备[2-4]。
喷雾冷冻干燥法制备的纳米粉,粒径大小不同,从几纳米到几百纳米不等。造成粒径不同的原因:一方面与样品本来形态和前驱体的制备方法有关;另一方面是与喷雾冷冻干燥过程中冻结速率、最终冻结温度等工艺参数有关,近年来引起了研究人员的关注。Sebastião等[5]建立了一系列常压喷雾冷冻干燥过程的数学模型,模型包括单液滴冻结模型、冻结过程传热模型和干燥过程传热模型。喷雾冻结过程对喷雾冷冻干燥产品质量有较大的影响,研究表明,低温冻结过程中液滴冻结速率能够有效影响冻干后物料的粒径尺寸,并且能够提高产品的质量[6-9]。
目前限制喷雾冷冻干燥技术推广应用的主要因素是冻结过程、冻结速率和冻结温度不易精确控制[10]。因此,建立喷雾冻结过程的数学模型,通过CFD和实验对喷雾冻结过程进行仿真和验证,分析液滴粒径、氮气流量和物料流量等因素对物料最终冻结温度、冻结速率的影响规律,为精确控制冻结温度和冻结速率提供理论基础。
1 模型的建立
1.1 物理模型
喷雾冷冻设备的冻干室结构存在的相变主要为液态物料放热并相变为固态物料,氮气吸热温度升高,液体汽化与冰升华虽然存在,但相比之下量很少可以忽略不计。为了便于研究,将冻干室结构简化,简化后物理模型如图1所示,其内层腔体直径为180 mm,高度为380 mm;外腔直径260 mm,高度为420 mm。
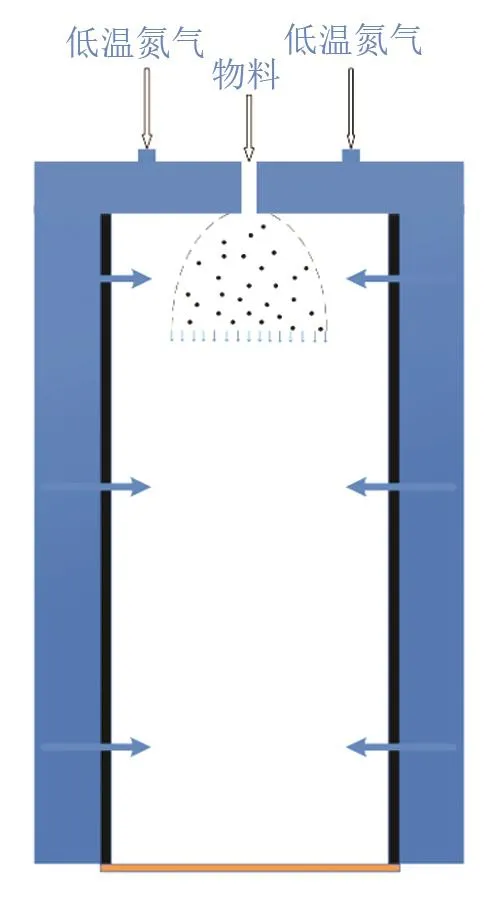
图1 冻干室结构的简化物理模型Fig.1 The simplified physical model of the lyophilisation chamber structure
1.2 数学模型
1.2.1 液滴位移模型
雾化液滴在整个冻结过程做斜抛运动,在简化模型时定义所有雾化液滴初始速度的竖直分量均为vz,因此整个下落过程液滴各位置的竖直方向加速度a可以根据牛顿第二定律计算:

式中:g为重力加速度;Ff为阻力(拖拽力);md为液滴质量;a为液滴在某点的加速度。
雾化液滴在向下运动过程中会受到相应的气体阻力Ff,气体阻力可以由式(2)进行计算。

式中:dd为液滴直径;ρg为气体密度;vz为液滴在某点的速度。
阻力系数μ可以根据式(3)进行求解。
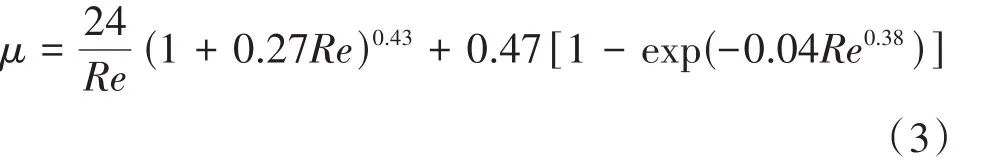
式中:Re为雷诺数。
雾化液滴在运动一段时间t后,雾化液滴所处的冻干室内位置可以由液滴向下运动的竖直位移xz表示,xz可以根据式(4)和(5)联立求解。

式中:t为液滴运动到某点时的时间;v0为液滴竖直方向初始速度。
1.2.2 喷雾冻结过程单液滴冻结模型
在使用集总热容法时要考虑实际情况中的毕渥数Bi的范围,毕渥数Bi可以根据式(6)进行求解:

式中:hd为液态液滴对流换热系数;k为热导率。
为减小使用集总热容法时带来的误差,要求Bi<0.1时才使用集总热容法。设液滴直径dd=0.000 1 m,水的导热系数kwater=0.566 W/(m·K),冰的导热系数kice=2.26 W/(m·K),对流传热系数hd=150 W/(m2·K)[11],雾化物料为液态或固态时毕渥数Bi均小于0.1,因此水的喷雾冻结过程可以使用集总热容法。
采用集总热容法建立液滴冻结速率模型,液滴内部温度梯度忽略不计,则液滴温度降至共晶点温度TP时,所需时间t1与降温速率vT1为:
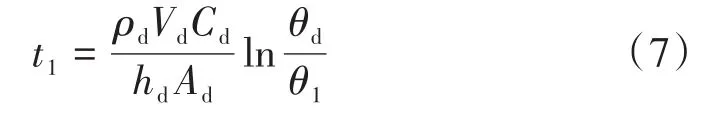
式中:ρd为液态液滴密度;Vd为液滴体积;Cd为液态液滴比热容;Ad为液滴表面积;θd为液滴与氮气的温度差;θ1为液滴相变温度与氮气温度之间的差。

式中:Td为液滴温度;Tp为液滴相变温度;t1为液滴温度降至共晶点温度所需时间。
根据体积Vd与表面积Ad公式:

式(7)可以改写为:

式中:ρd为液态液滴密度;Tgi为氮气温度。
相变阶段时,液滴相变时间t2与相变传热总能量Q2之间的关系为:
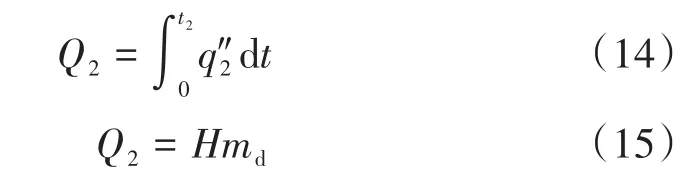
式中:q″2为液滴相变阶段的热流密度;H为液滴冻结潜热。
冰粒降温阶段,冰粒从共晶点温度Tp至预设最终冻结温度Tice所需时间t3:
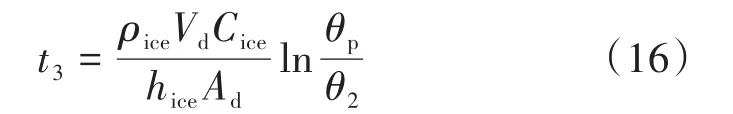
式中:ρice为冰的密度;hice为冰粒对流传热系数;Cice为冰粒的比热容;θp为共晶点温度与氮气温度之差;θ2为冰与氮气之间的温度差。

式中:Tp为共晶点温度;Tice为冰的温度。
1.2.3 喷雾冻结过程能量传输模型
建立喷雾冻结过程中雾化液滴与氮气之间的能量传输模型[12-13],并预测氮气的实时温度Tgi。雾化液滴从雾化喷嘴喷出时的初始温度Td0,直至液滴冻结并降温至相变温度以下T,所释放热量Qz为:
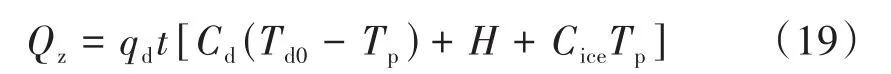
式中:Qz为液滴在整个喷雾冻结阶段释放总热量;qd为液滴流量;Td0为液滴初始温度。
在整个过程中氮气吸收的热量包括雾化液滴释放的热量、冻干室壁面降温所释放的热量以及外界辐射传热所传输的热量。在此过程中氮气吸收的热量Qx与雾化液滴释放的热量Qz相等,即Qx=Qz。氮气另外吸收的热量定义为氮气系统的热损失,设热损失系数为λ。氮气在冻干室的出口温度与氮气热量变化之间的关系为:
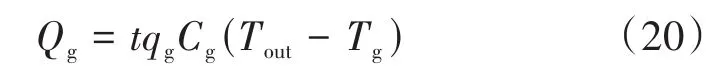
式中:Qg为氮气在整个喷雾冻结阶段释放总热量;qg为氮气流量;Cg为氮气的比热容;Tout为出口氮气温度;Tg为入口氮气温度。
氮气吸收的热量Qx为:
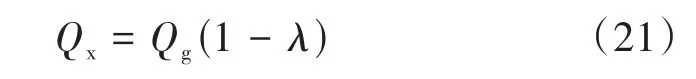
2 数值模拟结果与分析
本文利用Fluent模拟了喷雾冻结过程,采用SIMPLE算法求解器求解[14-16]。模拟仿真前对建立的冻干室模型进行网格划分,如图2所示,并将模拟过程的边界条件设置如表1所列。
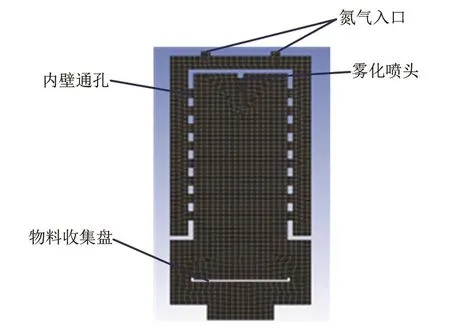
图2 冻干室模型网格划分Fig.2 Freeze-drying chamber model meshing

表1 仿真过程中的边界条件设置Tab.1 Boundary condition settings during the simulation
2.1 氮气流量与最终冻结温度和冻结速率间的响应规律
根据模拟仿真,当液滴流量为5 g/s,氮气初始温度为150 K,氮气流量分别为40 g/s、50 g/s和60 g/s时,雾化液滴温度图像如图3所示。在冻干室内设置三个不同位置的监测点,对3个监测点液滴温度进行测量分析(如图4所示),得出冻干室内不同位置液滴温度与氮气流量之间的关系图,如图5所示。

图3 不同氮气流量雾化液滴温度分布图Fig.3 Temperature distribution of atomized droplets with different nitrogen flow rates
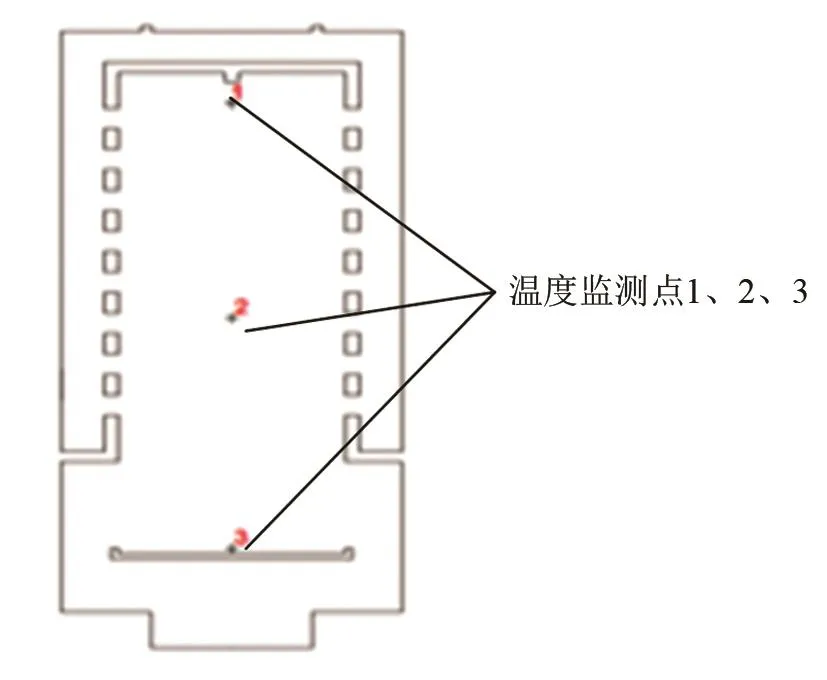
图4 监测点位置Fig.4 Location of monitoring points
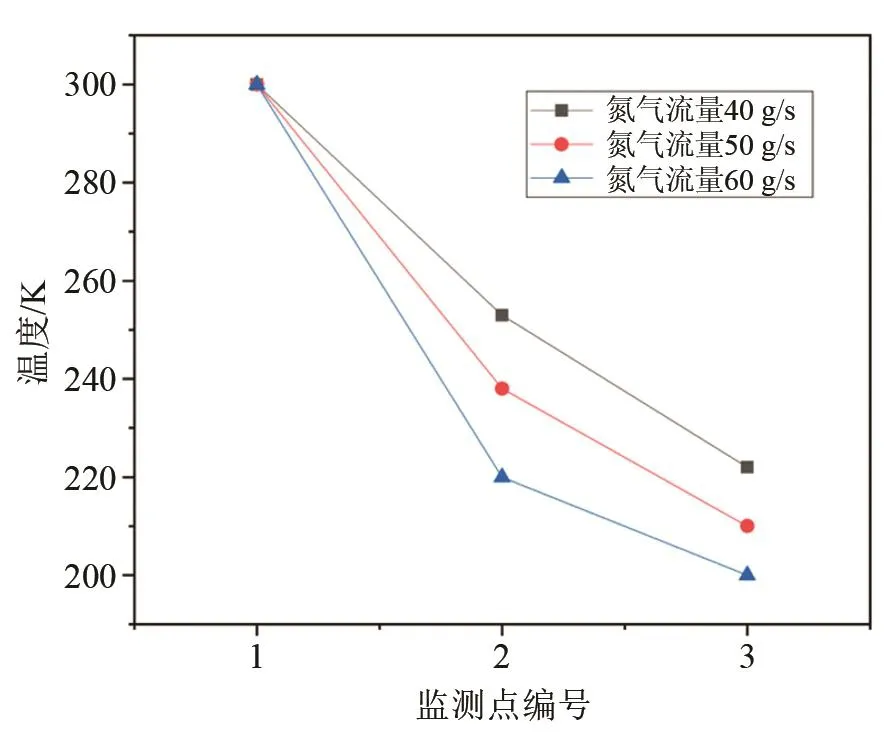
图5 监测点液滴温度变化图Fig.5 The droplet temperature change diagram at the monitoring point
如图6所示,将喷雾冻结过程最终冻结温度数学模型求解结果与模拟结果对比,可知数学模型求解结果与模拟结果趋势相同,最终冻结温度最大相差10 K,最大误差率为4%。

图6 氮气流量与液滴最终冻结温度的关系Fig.6 Relationship between nitrogen flow rate and final freezing temperature of droplets
液滴自雾化器喷出降落至物料收集盘所需时间约为0.13 s,结合图5中监测点1与监测点3温度差可计算出模拟过程氮气流量液滴平均冻结速率。对比液滴在冻结过程中平均冻结速率的数学模型求解结果与模拟结果,如图7所示,当氮气流量在40 g/s左右时误差较大,最大相差20 K/s,最大误差率为3.3%。
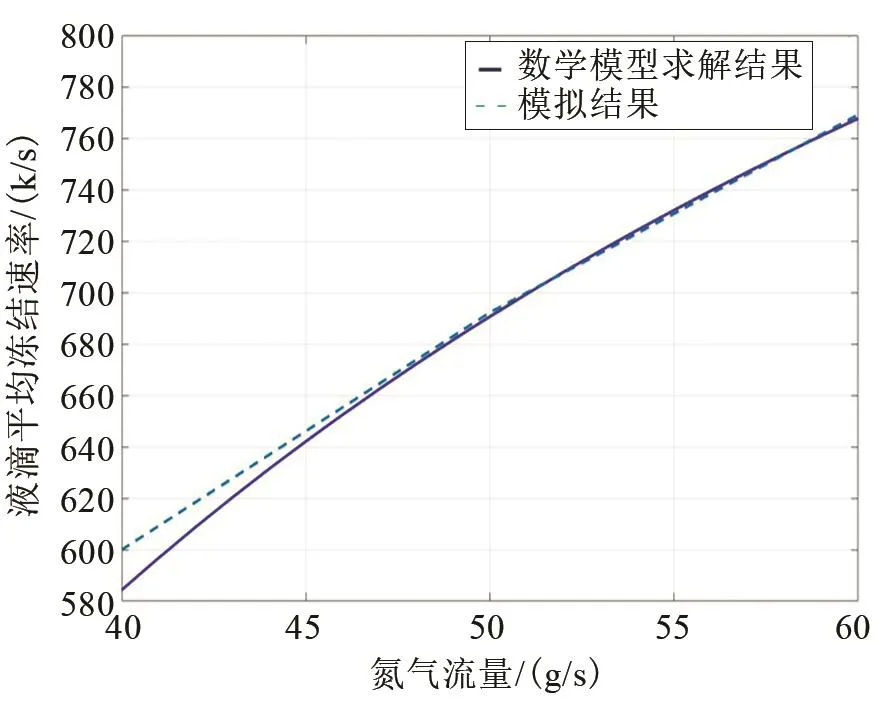
图7 氮气流量与液滴平均冻结速率的关系Fig.7 Relationship between nitrogen flow rate and average droplet freezing rate
2.2 物料流量与最终冻结温度和冻结速率间的响应规律
当氮气流量为40 g/s,液滴流量分别为3 g/s、5 g/s和8 g/s时,仿真过程稳定后雾化液滴温度图像如图8所示。对监测点液滴温度进行分析,得出冻干室内不同位置液滴温度与氮气流量之间的关系,如图9所示。

图8 不同液滴流量雾化液滴温度分布图Fig.8 Temperature distribution of atomized droplets with different droplet flow rates
将喷雾冻结过程最终冻结温度数学模型求解结果与模拟结果对比,如图10所示,数学模型求解结果与模拟结果趋势相同,最终冻结温度相差在10 K以内,最大误差率为3.7%。结合图9中监测点1与监测点3温度差可计算出模拟过程中液滴的平均冻结速率。

图9 监测点液滴温度变化图Fig.9 The droplet temperature change diagram at the monitoring point
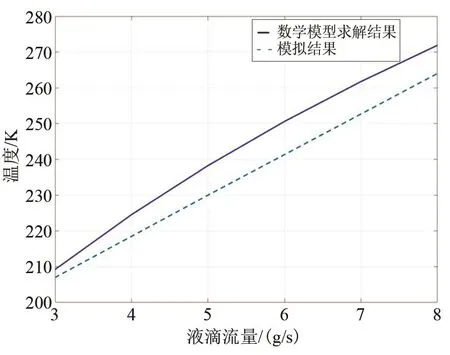
图10 液滴流量与液滴最终冻结温度的关系Fig.10 The relationship between droplet flow and final freezing temperature of droplets
如图11所示,当氮气流量不变,液滴流量逐渐增大到4 g/s时误差逐步减小,当液滴流量从4 g/s增大时误差逐步增大,最大误差率为7.1%。

图11 液滴流量与液滴平均冻结速率的关系Fig.11 The relationship between droplets flow and the average freezing rate of droplets
3 实验结果与数学模型求解结果的对比分析
在改进后的实验型喷雾冷冻干燥机上进行喷雾冻结实验。实验初始条件为:氮气初始温度为103 K,液滴粒径为30 μm,物料流量为3 g/s,通过调节氮气出口阀压力来控制氮气流量,压力维持在0.3 MPa,然后进行喷雾冻结实验[17-18]。以相同的条件在实验型喷雾冷冻干燥机上重复3次实验,实验结果如图12所示,实验结果平均值如图13所示。
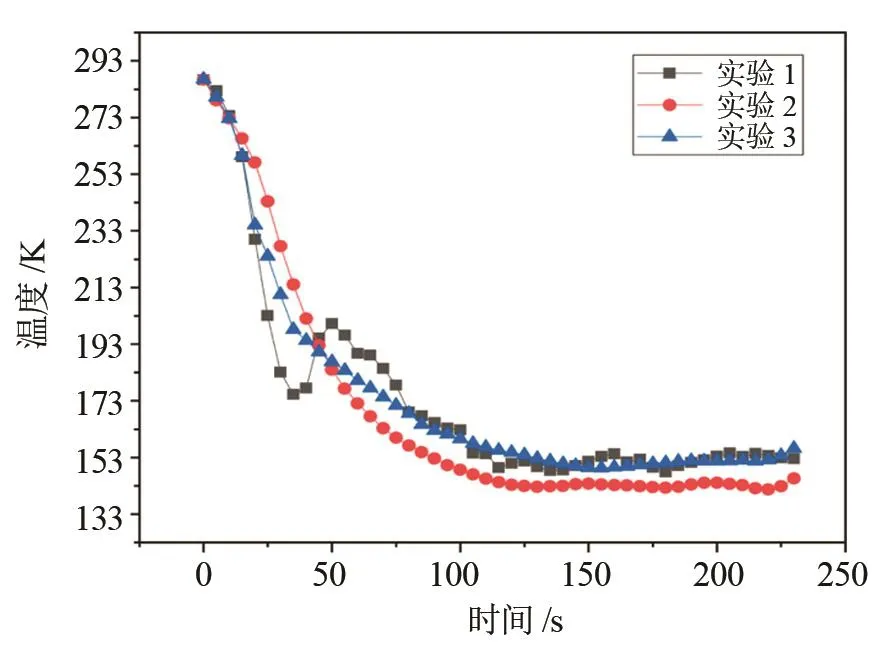
图12 喷雾冻结实验最终冻结温度Fig.12 The final freezing temperature of the spray freezing experiment
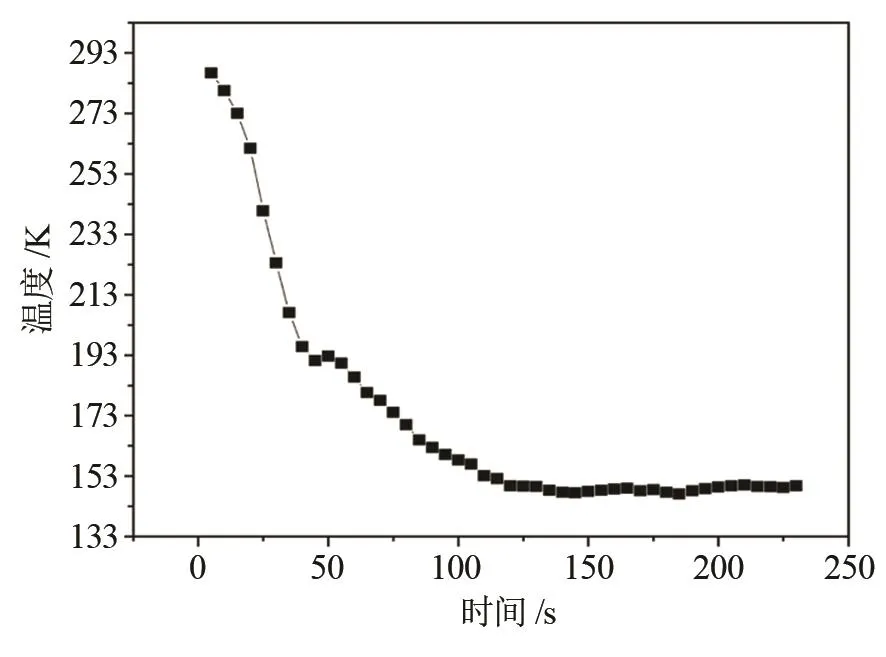
图13 喷雾冻结实验平均最终冻结温度Fig.13 The average final freezing temperature of the spray freezing experiment
氮气入口压力选择及对应氮气流量如表2所列。不同氮气流量下监测点2、3雾化液滴最终冻结温度如表3所列。

表2 不同氮气入口压力下相应氮气流量Tab.2 Corresponding nitrogen flow rate under different nitrogen inlet pressures
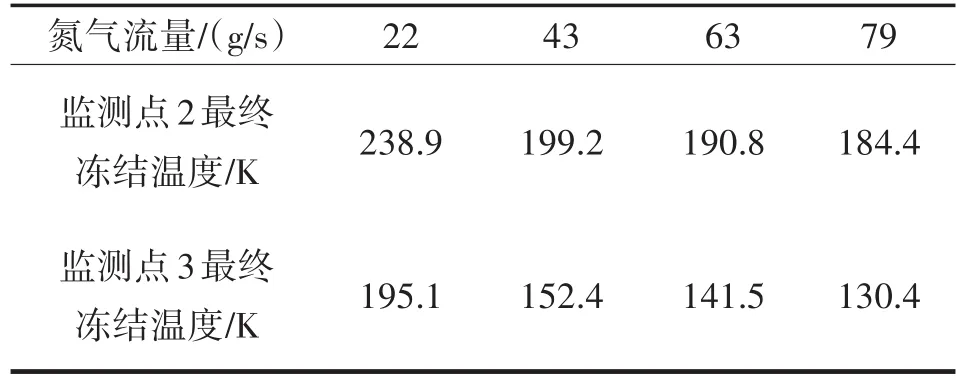
表3 不同氮气流量下监测点2、3最终冻结温度Tab.3 Final freezing temperature of monitoring points 2 and 3 under different nitrogen flow rates
将表3的实验结果与数学模型求解结果对比,如图14所示。
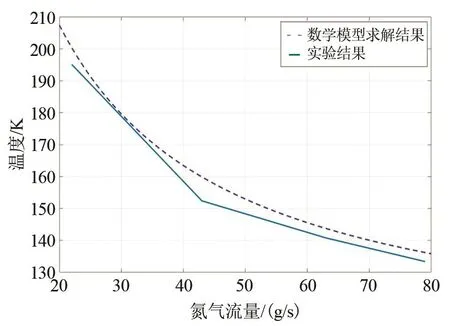
图14 最终冻结温度与氮气流量关系Fig.14 The relationship between final freezing temperature and nitrogen flow
由图14可知,氮气流量对最终冻结温度影响趋势的实验结果与数学模型求解结果基本一致,数值结果较为接近,最大相差不超过8 K,数学模型求解结果相对实验结果最大误差率为5.2%。
4 结论
采用集总热容法建立了喷雾冻结过程的数学模型,求解得到氮气流量和液滴流量对液滴最终冻结温度和冻结速率的影响规律。为验证所建立数学模型的准确性,以水为对象利用Fluent软件对喷雾冻结过程进行了模拟仿真,将模拟仿真结果与数学模型求解结果对比发现:平均冻结速率最大相差不超过20 K/s,最大误差率为7.1%;最终冻结温度两者相差在10 K以内,最大误差率为4%,可能是仿真所设置的边界条件不够精确导致出现了误差。但从整体上看,数学模型求解结果与模拟仿真结果吻合度较好,验证了数学模型的准确性。
利用改进后的实验型喷雾冷冻干燥机进行验证实验。对比实验结果发现,喷雾冻结实验结果与数学模型求解结果最大相差8 K,相对实验结果误差率最大为5.2%。该数学模型可以为建立喷雾冻结自动控制系统提供一定的借鉴。
