磁悬浮转子真空计混合磁悬浮建模与控制研究
2023-02-14李博文李得天习振华郭美如周明旭
李博文,李得天,*,习振华,郭美如,周明旭
(1.兰州空间技术物理研究所 真空技术与物理重点实验室,兰州 730000;2.东北大学 机械工程与自动化学院,沈阳 110819)
0 引言
磁悬浮转子真空计(Spinning Rotor Gauge,SRG)具有优异的长期稳定性和重复性,在真空计量领域作为传递标准使用[1-2]。但是,受残余阻尼、温度、外部振动等因素影响,磁悬浮转子真空计的量限拓展、准确度提高以及使用范围受到了严重制约。混合磁悬浮转子真空计利用永磁-电磁合力使转子稳定悬浮在真空中,转子与支撑件之间没有任何机械接触,仅凭借测量气体分子对转子旋转阻尼作用的大小来测量真空压力[3]。
混合磁悬浮转子真空计是基于Beams等的纯电磁磁悬浮真空计发展而来的[4]。上世纪80年代,Fremery等[5]完善了真空计的混合磁悬浮结构,解决了纯电磁磁悬浮真空计的功耗大、发热大、悬浮不稳定导致的测量失真等问题[6]。至今为止,鲜有人对于这种独特的混合磁悬浮系统中永磁力与电磁力在磁悬浮过程中的影响与配比关系作出报道。为进一步探索提高磁悬浮转子真空计的测量精度,本文将推导磁悬浮转子真空计的混合磁悬浮的磁场关系,得到频域模型;并将电磁线圈参数与永磁体参数引入模型,研究SRG独特的混合磁悬浮系统物理模型的建立及其控制;最后利用数学模型中引入的参数指导实际磁悬浮系统的搭建,并进行压力测量实验。为磁悬浮转子真空计悬浮稳定性的进一步提高和测量上下限的扩展提供理论基础[7-13]。
1 永磁-电磁混合磁悬浮模型
1.1 纯电磁悬浮模型
要实现转子的无摩擦悬浮,通常首先考虑采用电磁悬浮系统。这是一种较为成熟的技术,在各个领域都有较为成熟的模型可以参考。在本文所研究的问题上,纯电磁磁悬浮(即仅仅使用电磁线圈使球形转子悬浮)也是一种值得考虑的选择。模型示意如图1所示。
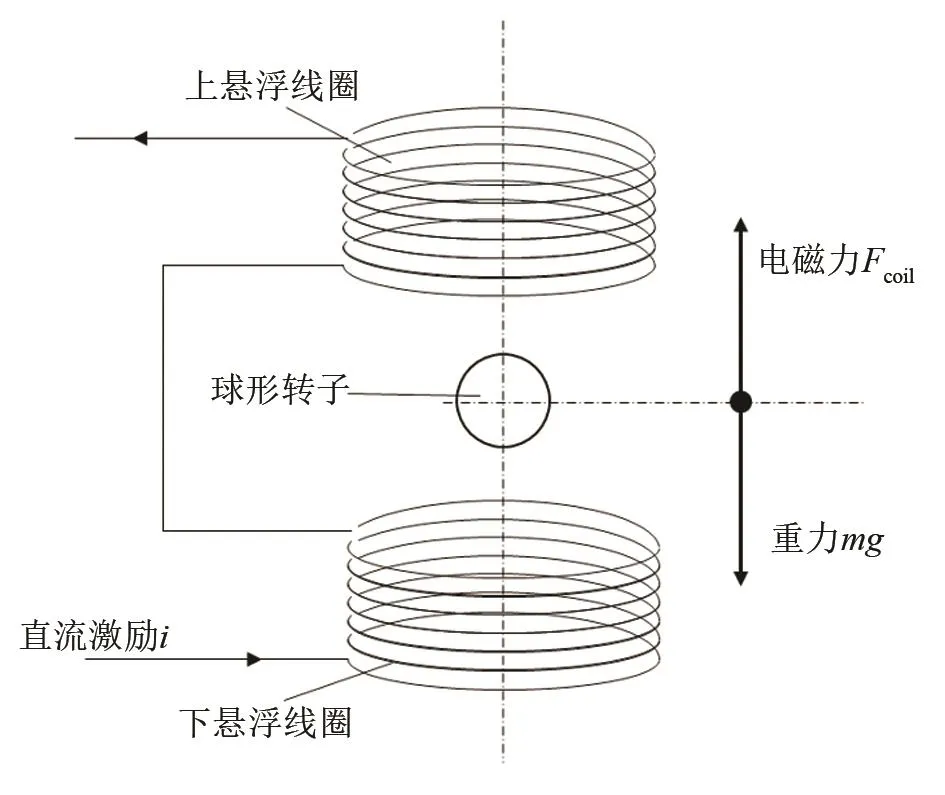
图1 球形转子电磁悬浮示意图Fig.1 Schematic diagram of electromagnetic levitation of rotor
实际工作中,要求真空计长期不停机工作,磁悬浮系统尽可能功耗低,因此会增加一个外力承载一部分转子的质量,减轻电磁线圈的负载。为此,引入永磁体,形成电磁-永磁混合磁悬浮结构。
1.2 混合磁悬浮模型
磁悬浮转子真空计的混合磁悬浮系统结构如图2所示,球形转子位于中间位置,上下各有一块极性同向的永磁体,两个串联的电磁线圈在转子上下对称布置。在实际应用中,在这一对串联的电磁线圈上加载直流信号用以产生电磁力。为准确估计闭环系统的固有特性,必须对转子悬浮系统进行精准的建模,尽可能地考虑到影响轴向悬浮系统中的所有因素。为研究方便,在不影响模型建立与实验的前提下,做如下假设:

图2 混合磁悬浮系统结构图Fig.2 Structure of hybrid magnetic levitation system
(1)永磁体均匀磁化,且轴向磁场的磁势不随时间或温度发生衰减;
(2)铁磁材料(即球形转子与永磁体材料)的磁导率无限大;
(3)忽略线圈与永磁体在气隙中的漏磁;
(4)假定球形转子、线圈、永磁体刚度无限大,不发生任何弹性形变;
(5)忽略测量气体对转子的作用;
(6)忽略法兰管对电磁场的影响。
图2中红框为实际系统中的法兰管,连接至真空系统并限制转子的运动。Fm与Fup(x,i)和Fdown(x,i)作用,转子悬浮的动力学方程为:
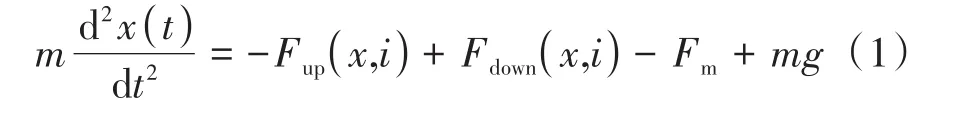
首先对永磁体在中心轴线处的磁感应强度进行分析,建立如图3所示的圆柱形永磁体中心轴线上的磁感应强度模型。
由假设(1),永磁体均匀磁化,磁化强度M为常矢量,因此体电流密度为零。由安培分子环流定律,可将圆柱形永磁体等效为一个沿圆柱侧面切线方向流动的,电流大小为M且上下顶面无电流的圆筒形环流。取如图3所示的圆柱面微分长度为dz0,圆柱面到底面距离为z0,a为永磁体半径,θ0为环流电流通过的角度,在dz0上流动的面电流为Mdz0θ,则此面电流在P点产生的dBm为[14]:

图3 圆柱形永磁体轴向磁感应强度模型Fig.3 Model of axial magnetic field strength of a cylindrical permanent magnet
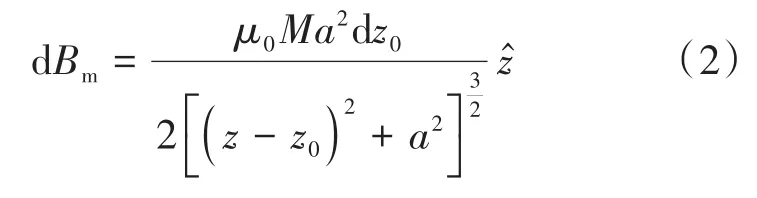
沿圆柱高度积分,可以得到圆柱形永磁体在中心轴线上P点产生的磁感应强度Bm为:
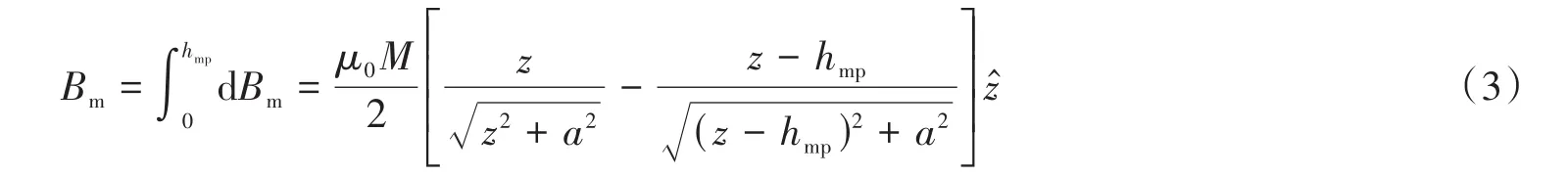
即在P点处有:
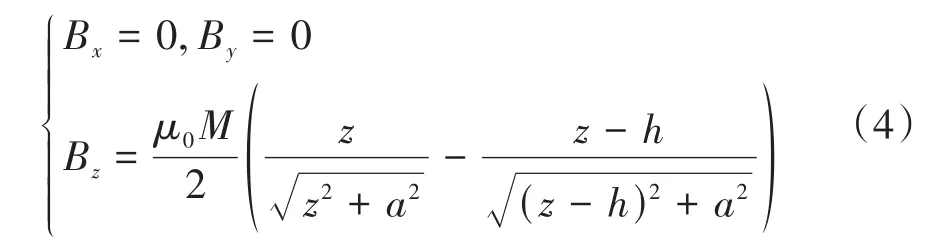
式中:μ0为空气磁导率;为由原点指向坐标轴z方向的单位矢量。
由式(3)可以看出,若两块永磁体以中心位置对称,则永磁体在轴线中心位置产生的磁感应强度会相互抵消,不能起到平衡转子的部分重力的作用。在实际设计中也考虑到了这个问题,因此上下永磁体为非对称布置,如图2所示,上下永磁体与线圈距离不同,上方永磁体更靠近线圈,提供更强的磁力。
根据以上推导,得到永磁体在中心轴线方向上产生的永磁力与磁感应强度方程组为:

式中:Bmup为下永磁体在转子径向平面处产生的磁感应强度;Bmdown来自上永磁体;S为转子截面积。综合上述方程组,可以得到在空间中某位置永磁体对转子的磁力为:

由式(6)可知,永磁体对转子的作用力仅与转子轴向悬浮位置x有关。因此,一旦通过电磁线圈控制回路的设计确定了转子轴向悬浮位置x,转子所受永磁力就仅受永磁体的安装位置sdown与sup制约。因此在混合磁悬浮系统的设计中可以根据转子质量调整永磁体的相对安装位置。
由磁路的基尔霍夫定律与毕奥-萨伐尔定律推导电磁线圈产生的电磁力,线圈对转子的吸引力可以表示为:

式中:N为线圈匝数;0.01为上下线圈距离,单位为m,为简化计算,令常数项:

综合式(1)~(9),可得转子悬浮的运动学方程:
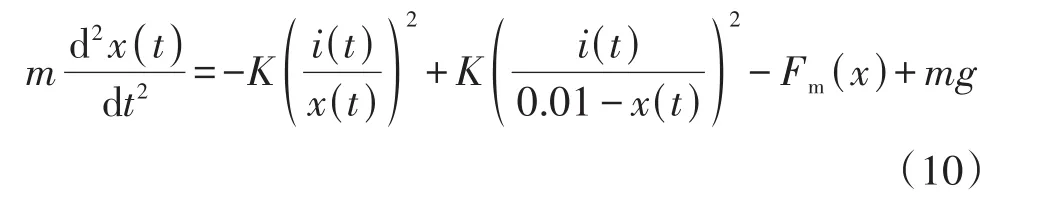
当工作在平衡点时(即两线圈间几何中心点,距下线圈5 mm处),由式(10)知,此时上下线圈的电磁力大小相同、方向相反,力学平衡中电磁力项为零,永磁体的磁力与球形转子所受重力相互抵消。物理意义为:当球形转子到达这一理想位置,即形成力学平衡,线圈上将不加载电流。而这是不符合实际工况的,由恩绍定理可知,单一永磁体的磁力不可能产生稳定的磁悬浮,因此在计算时,结合实际情况,选择一微小偏差量作为修正,即取x0=0.005 1 m。工作电流为i0,为尽可能达到小功率甚至零功率控制,此处设置期望电流为0.01 A。
由式(10)可以看出转子的磁悬浮控制是一个非线性系统,在平衡位置附近进行线性化处理,得到线性化后的运动学方程为:

其中:


式中:Kx与Ki为永磁悬浮位移刚度系数和永磁悬浮电流刚度系数。
将式(11)进行拉普拉斯变换,可得:

移项化简得到:

由式(15)可知,混合磁悬浮系统频域模型与电磁悬浮系统相似[15],均由“电流刚度系数”与“位移刚度系数”来表征线圈电流变化与悬浮转子位移变化对系统影响的系数,但从式(12)可以看出,推导出的位移刚度系数中含有与永磁体磁化强度、尺寸、安装位置等参数相关的变量。具体参数如表1所列。

表1 混合磁悬浮系统部分参数表Tab.1 Partial parameters of hybrid magnetic suspension system
代入表中参数得到混合磁悬浮系统的传递函数,这是一个二阶系统:
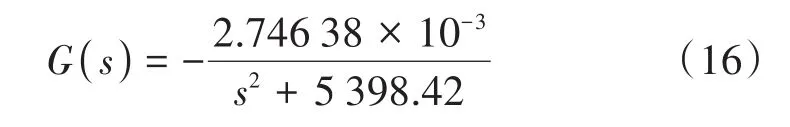
由劳斯判据可知,系统不稳定,必须增加控制器来保证转子的稳定悬浮。
表1中,模型采用空心线圈实现电磁悬浮部分,且球形转子直径小于线圈内径,因此可以认为转子仅受穿过其径向截面的磁通作用,因此在计算电磁力时均采用转子的截面积S。
2 仿真分析
使用PID控制器对推导出的二阶系统进行控制,选取较为快速的悬浮控制参数。参照第一章搭建磁悬浮转子真空计的混合悬浮模型,为更接近实际工况,采用离散模式,采样周期T=0.001,系统的仿真模型框图如图4所示。
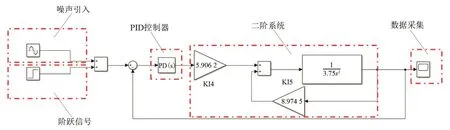
图4 二阶系统的仿真模型框图Fig.4 Simulation model block diagram of second-order system
2.1 阶跃响应实验
通常的外来噪声,如抽气系统产生的噪声信号、实验环境中其他噪声等干扰会引发振动,为此,在阶跃信号的基础上,加入幅值为0.000 01的白噪声信号以模拟环境噪声,进行仿真实验,结果如图5所示。
从图5可以看出,由于式(16)表示的混合磁悬浮系统在频域表达式上为二阶系统,其固有特性类似“低通滤波器”的作用,系统响应受白噪声信号的高频分量影响较小,低频噪声保留较多,因此可知此混合磁悬浮系统易受低频噪声的干扰。
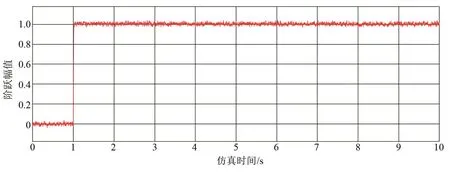
图5 模拟噪声下混合磁悬浮系统的阶跃响应Fig.5 Step response of hybrid magnetic levitation system under simulated noise
2.2 频域分析
为定量检验对高频噪声的抑制效果,对图5中的悬浮响应信号进行傅里叶变换,观察其频域特征,结果如图6所示。
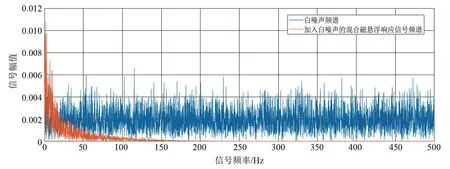
图6 加入白噪声的混合磁悬浮系统响应信号与白噪声信号频谱对比图Fig.6 Spectral comparison plot of the response signal of the hybrid magnetic levitation system and the white noise signal
从图6可以看出,悬浮信号的低频振动集中在150 Hz以内,远离磁悬浮转子真空计的工作频率350~550 Hz,对测量系统获得较优质的转子旋转信号影响较小。
3 控制器设计
设计模拟比例-积分-微分控制电路。控制器原理框图与实物图如图7所示。

图7 PID混合磁悬浮系统控制器原理框图与实际电路图Fig.7 Hybrid magnetic levitation system controller block diagram and actual circuit diagram
4 模型验证
为验证混合磁悬浮模型的正确性,以兰州空间技术物理研究所自研的磁悬浮转子真空计为对象进行试验。利用频率计数器对磁悬浮控制系统的悬浮位移响应进行频域分析。
通过前一章节搭建的磁悬浮PID控制电路实现悬浮转子悬浮,并采集其悬浮信号,以便对其悬浮响应进行时域与频域研究。
调整PID参数至稳定悬浮后记录悬浮位移响应曲线,如图8所示。

图8 混合磁悬浮系统中球形转子的悬浮响应信号Fig.8 The suspension response signal of a spherical rotor in a hybrid magnetic levitation system
由图8可以看出,悬浮较为稳定,轴向位置波动量在±0.06 mm以内。
悬浮实物图如图9所示。设空间中心位置为参考位移点,调整PID参数,将位移信号引至频率计数器,进行12 000个频率点的采样,结果如图10所示。

图9 混合磁悬浮系统实物图Fig.9 Physical drawing of hybrid magnetic levitation system
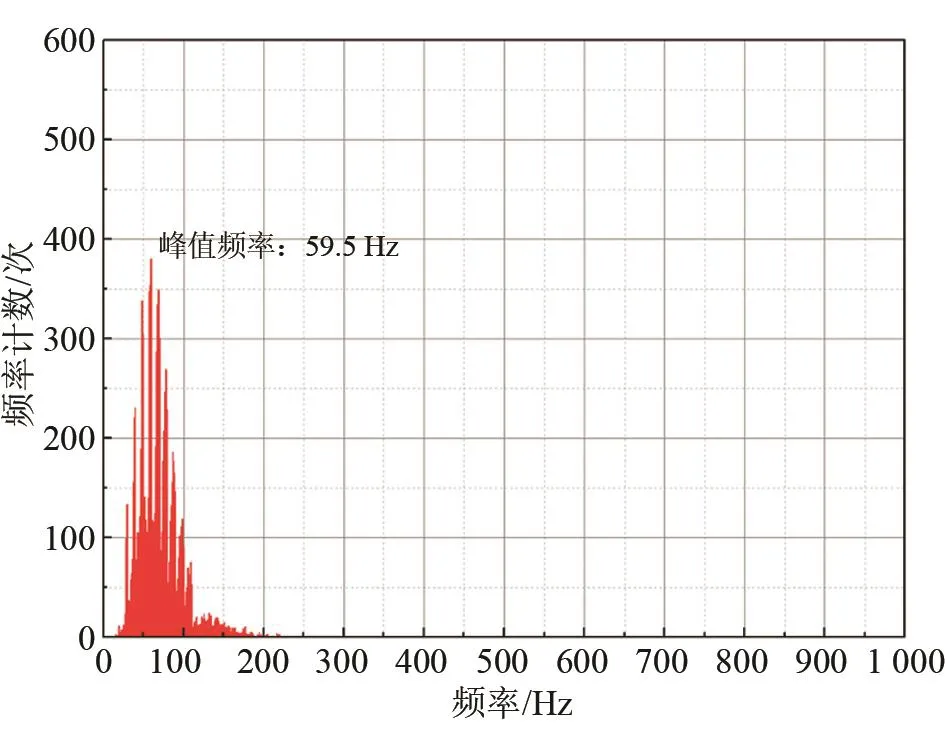
图10 混合磁悬浮系统中球形转子悬浮信号的频率直方图Fig.10 Histogram of the frequency of the levitation signal of a spherical rotor in a hybrid magnetic levitation system
由实验结果可以看出,图8与图10显示的悬浮过程中的低频振动现象与图5、图6的仿真结果吻合。通过频谱计数结果(图10)可以看出,在PID控制器的控制下,悬浮信号频域显示150 Hz以内存在低频振动,振动频率谱峰值处位于59.5 Hz处。与仿真结果(图6)基本一致。
5 压力测量实验
将磁悬浮控制模块电路接入到磁悬浮系统中进行压力测量实验,一个月内进行4次9×10-5~1 Pa的压力测试,将得到的压力结果与标准压力进行对比,如图11所示。

图11 压力测量实验结果对比Fig.11 Comparison of pressure measurement experiment results
由图中实验数据可以看出,混合磁悬浮系统可以长期稳定工作,保证了混合磁悬浮真空计对压力的准确测量。混合磁悬浮转子频域数学模型的建立,量化了永磁体与线圈在磁悬浮过程中的影响,为稳定、低功耗、长期工作的磁悬浮系统搭建打好了基础。
6 结论
本文设计了永磁-电磁混合磁悬浮系统参数并建立了该系统的频域模型,根据劳斯判据分析了系统稳定性。最后通过搭建模拟PID电路,进行了闭环PID控制的实验,对信号进行频域分析,验证了频域模型的正确性。通过以上的研究得到了以下结论:
(1)通过数学模型仿真与实验对比,发现转子的低频振动来自混合磁悬浮控制系统的闭环控制固有频域特性与白噪声的激发,印证了混合磁悬浮二阶模型的正确性;
(2)经过近30天的压力测试实验,磁悬浮测量头持续准确地测量出压力,证明未发生转子悬浮的不稳定带来的本底变化,磁悬浮系统维持低功耗悬浮运行。验证了由数学模型得到的线圈参数、永磁体参数与安装位置的合理性。
仿真结果与实验结果的细微差别和实际悬浮中的低频抖动表明,磁悬浮系统中仍有部分因素在建立模型时未被考虑到。有待进一步实验研究,细化模型。
